Barbin.html

Ce qui fait la qualité de l'inventivité et de l'imagination du chercheur,
c'est la qualité de son attention, à l'écoute de la voix des choses.
Car les choses de l'Univers ne se lassent jamais de parler d'elles-mêmes
et de se révéler, à celui qui se soucie d'entendre.

A. Grothendieck, Récoltes et semailles, 1985.

I Notes de lecture sur l'article de E. Barbin : "La démonstration : pulsation entre le discursif et le visuel". Sommaire I

Avertissement : pour chaque paragraphe j'essaie de faire un résumé succint en retenant ce qui me (choix personnel) semble être sa substantifique moelle. Cela ne dispense pas d'aller lire l'article en question!...

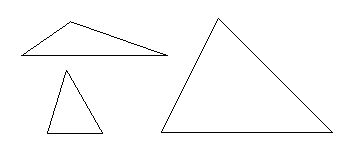
Il faut prendre conscience de la différence qu'il y a entre vue/regard, sensible/entendement. La vue de triangles disparates :

conduit au regard. Il y a ici quelque chose à voir et à dire (la somme des angles d'un triangles est égale à 180 degrés) : d'où le discours démonstratif.

(Page 34) La démonstration donnée par Euclide de la proposition 32 du livre I (la somme des angles d'un triangles est égale à deux droits) est analysée. C'est un discours qui porte sur une figure fixe. La mobilité de la figure, de l'oeil et du corps est remplacée par le déroulement du discours ; à savoir de différentes conjonctions (aussi, mais, donc, puisque).

(Page 35) Pour Euclide les figures sont immobiles. Les axiomes sont répartis en demandes et notions communes. Les demandes règlementent la façon dont il est légitime de construire des lignes supplémentaires : elles concernent le mouvement de la main. Les notions communes concernent plutôt le mouvement de l'oeil. Nous avons dit que le passage de l'ob-jet triangle de la vue, à l'objet triangle de l'entendement s'effectue par une mobilité du corps et une mobilité de l'oeil. Dans le discours axiomatique, le passage de l'ob-jet de la définition à ce qui va devenir l'objet immobile de la démonstration s'effectue par des axiomes où se disent des mobilités du corps, dans des constructions, et des mobilités de l'oeil, dans des transports d'égalités.

(Page 38) Les démonstrations des proposition 1 ("sur une droite limitée donnée, construire un triangle équilatéral") et proposition 2 ("placer en un point donné, une droite égale à une droite donnée") du Livre I sont analysées. Le discours démonstratif est le règne du donc (prop. 1). Il s'agit de pouvoir déduire par le discours la validité d'une construction (prop. 2). Dans le discours démonstratif, la nécessité de l'énoncé ne tient pas une évidence en tant qu'affect de l'entendement. D'une certaine façon, toute l'évidence de ce discours est concentré dans l'énoncé des axiomes.
Le discours de la nécessité est le passage des hypothèses aux conclusions par un jeu de et de donc.

(Page 40) Hérigone introduit un symbolisme pour signifier puisque et donc. Il rompt avec le caractère linéaire des démonstrations d'Euclide en utilisant les deux dimensions du papier, ce qui est mis en évidence par l'étude de la démonstration du fait : "étant données deux lignes droites, décrire un cercle qui touche les deux lignes données". Sa disposition en colonnes ne convient toutefois pas au discours démonstratif, car il n'y pas de symbole pour indiquer l'ordre d'enchaînement des assertions. Faire une démonstration demande, avant tout acte d'écriture, une nécessité de l'entendement, et c'est cela qui est la source première de la difficulté des élèves, car, sans l'appréhension de cette nécessité, la démonstration n'a aucun sens. Passer outre cette nécessité produit du non-sens, et supprimer le caractère nécessaire du discours est insensé.

(Page 42) Sont opposées les démonstrations du théorème de Pythagore données par le grec Euclide par le chinois Lui-Hui. La démonstration est discursive, la démonstration chinoise est visuelle (déplacement de figures). Pour Schopenhauer, la démonstration euclidienne est absurde parce qu'elle s'appuie sur l'évidence logique au lieu de s'appuyer sur l'évidence géométrique, sur un discours, et non sur la perception d'une figure. (...) Entre les démonstrations grecque et chinoise, il y a un renversement du fixe et du mobile : la première contemple une figure immobile et déroule son discours, la seconde repose sur la mobilité de la figure et offre un dire qui n'est pas mobilisé dans un discours.

(Page 45) Clairaut donne une démonstration du théorème de Pythagore qui utilise un jeu de composition de figures et n'hésite pas à s'en remettre à l'évidence visuelle. Il dit j'en use de la sorte (...) parce que j'ai remarqué que ceux qui avaient de la disposition à la géométrie se plaisaient à exercer leur esprit ; et qu'au contraire ils se rebutaient, lorsqu'on les accablait de démonstrations pour ainsi dire inutiles. (...) Tout raisonnement qui tombe sur ce que le bon sens décide d'avance, est aujourd'hui en pure perte, et n'est propre qu'à obscurcir la vérité, et à dégoûter les lecteurs.

(Page 47) Dire le mouvement revient à être capable de dire une infinité de figures, ce qui est impossible à l'époque de Zénon d'Elée et de ses paradoxes. C'est pour cela que les raisonnements concernant les aires de figures curvilignes doivent faire appel à des démonstrations dites par exhaustion, qui ne sont pas entièrement satisfaisantes, car elles sont indirectes et supposent que l'on connaît le résultat à démontrer. Archimède avait une méthode d'invention pour trouver ces résultats, et c'est la méthode (directe) des indivisibles, qui permettra de commencer à travailler avec l'infini.

(Page 49)Al-Khwarizmi utilise termes des termes imagés : racines (ce que l'on cherche), trésors (carrés des racines), et nombres simples qu'il combine entre eux pour former des équations du type "un trésor plus dix racines égalent trente-neuf dirhems". Il rédige des solutions de problèmes en termes de ces désignations. Et les explications qu'il donne sont en fait de nature géométrique. Il n'y a pas d'usage systématique des lettres.

2.2 Les règles du calcul algébrique : faire apparaître et faire disparaître. Sommaire I

(Page 52) Al-Khwarizmi est reconnu comme l'un des inventeurs de l'algèbre, terme qui vient de l'une des deux opérations qu'il introduit :
al-jabr (restauration), qui permet de passer un terme dans l'autre membre en le "changeant de signe" -- faire apparaître ;
l'autre est al-muqaba (confrontation), qui permet de supprimer un terme commun aux deux membres d'une équation -- faire disparaître.
L'algèbre c'est alors le savoir qui consiste en la maîtrise de ces opérations.
Lacroix (1803) est quelqu'un chez qui le recours à l'usage des lettres apparaît, libéré du recours aux figures. Il exprime les racines de l'équation x^2 + p x = q

(Page 53) La manière pour Euclide de démontrer est synthétique : il fait un discours dont on peut vérifier chaque étape et constater qu'elle est correcte, mais ce discours ne dit rien des idées en amont qui l'ont produit. Ce que déplore Descartes :
Certes, j'y [chez les Anciens] lisais sur les nombres une foule de développements dont le calcul me faisait constater la vérité ; quant aux figures, il y avait beaucoup de choses qu'ils me mettaient en quelque sorte sous les yeux mêmes, et qui étaient la suite de conséquences rigoureuses. Mais pourquoi il en était ainsi, et comment on parvenait à le trouver, ils ne me paraissaient suffisamment le montrer à l'intelligence elle-même.
L'utilisation de l'algèbre en géométrie permet de justifier de la nécessité de certaines constructions. La méthode de Descartes est analytique : elle progresse de l'inconnu vers le connu ; elle substitue l'évidence calculatoire à l'évidence visuelle.

(Page 54) Lamy est un adepte de Descartes. Il algébrise certaines démonstrations d'Euclide, et plaide pour un moindre recours aux figures :
(...) j'ai cru qu'il était bon de s'accoutumer à concevoir ces sortes de vérités sans se représenter des figures. (...) qui en plusieurs occasions ne peuvent être que confusion.

2.5 Les règles du calcul des équipollences : faire apparaître et faire disparaître. Sommaire I

(Page 56) En 1854, Bellavitis introduit une nouvelle méthode pour résoudre les problèmes de géométrie : les figures seront décomposées en droites simples, qui seront considérées comme des grandeurs et des directions.
Des règles régissent la manipulation de l'équipollence (un symbole oméga souligné) : les droites sont notées par deux lettres, disons AB ; on parle de leur inclaison inc. AB, de leur grandeur gr. AB. On peut considérer un multiple d'une droite.
On procède en faisant apparaître et disparaître des lettres, ce qui est un peu différent du recours à la relation de Chasles, lequel est plus subtil selon l'auteur. Pour se convaincre d'un résultat, il n'est plus nécessaire de regarder la figure : on regarde le jeu des formules.

(Page 57) Le même Bellavitis démontre que toute propriété des points d'une droite donne un théorème relatif aux points d'un plan, par le seul changement des équations en équipollences.
Il redémontre ainsi la Proposition 6 du livre d'Euclide : si une droite BD est divisée en C également, c'est-à-dire si BC = CD, et que A soit un point quelconque dans son prolongement, on aura : AB.AD + (BC)^2 = (AC)^2
La méthode consiste à partir de l'équation : b(b+2c)+c^2 = (b+c)^2 et à remplacer, Z étant un point arbitraire :
b par AZ-BZ ; c par BZ-CZ. L'hypothèse permet alors d'écrire BZ-CZ = CZ-DZ, ce qui permet de conclure.

(Page 58) Le mouvement dont il est question ici renvoie à quelque chose de précis (de sorte que la remarque provocatrice que je fais supra en II.2 est un peu frauduleuse) : celui qui est mis en jeu dans le calcul infinitésimal et différentiel. Les méthodes de Descartes ne permettent d'étudier que des courbes algébriques. L'étude de courbes transcendantes nécessite les méthodes développées par Leibniz et Newton : celle des "fluentes" et "fuxions" ; ancêtres des dérivations. Les manipulations des écritures mettant en jeu ces objets ne relèvent pas du même type d'opérations que celles misent en jeu dans un calcul algébrique (faire apparaître, faire disparaître). Ici on efface les termes négligeables.

(Page 59) René Guitart écrit : voir ce que l'on dit, dire ce que l'on voit, c'est impossible intégralement ; entre voir ce que l'on pense et dire ce que l'on pense, il y a une dialectique non-résolutive qui reste toujours un procès ouvert qui ne se referme que sur lui-même, soit plus précisément ce que j'appelle une pulsation. C'est la vivacité de cette pulsation, son incessante traversée sue et insue par l'entendement, qui forme la trame qu'emprunte le penser mathématique.

1 La valeur absolue : la fausse opposition algèbre/géométrie. Sommaire II

On peut aborder la notion de la valeur absolue d'un nombre réel x de deux façons parmi d'autres.

La première est celle préconisée par les instructions officielles, qui invite la considérer comme un outil qui permet de parler facilement de la distance entre deux nombres.
Cette approche est critiquable car elle réduit le contenu de cette notion à une simple à la portion congrue (une notation) : réduction en partie justifiée par... la réduction des horaires.

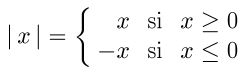
sur laquelle nous reviendrons par la suite. Quand on dit ici "démontrer", il faut comprendre que l'on donne un argument du type : il faut traiter séparément les trois cas :
- les deux nombres sont positifs,
- les deux nombres sont négatifs,
- il y en a un positif, et un négatif,
Ce que dans les faits, on ne fait pas : attitude justifiée en partie par... la réduction des horaires.
Cette approche est critiquable car elle s'oppose à ce qui dit Richard Dedekind : "En science, ce qui est démontrable ne doit pas être admis sans démonstration."

Donc, si on voulait apprendre à des élèves à faire quelquechose qui ressemble un peu à des mathématiques, il conviendrait :
- de prendre le parti de la négation ces deux approches en combinant ce que chacune a de meilleur ;
- de dépasser le débat truqué : cours magistral/autre chose, qui résulte -- pour ce qui est de l'enseignement des mathématiques en tout cas -- de la vraie opposition : méthode axiomatique/méthode génétique, qui s'est construite au début du siècle dernier, la réforme des mathématiques modernes ayant consacré le triomphe de la première au détriment de la seconde. (1)
C'est-à-dire qu'il faut s'appuyer sur une approche intuitive (première méthode) et voir ce qu'apporte une définition (deuxième méthode).

2 La valeur absolue : une notion relativement intéressante... Sommaire II

Si l'on voulait prendre en compte la pulsation, il conviendrait de se réapproprier (2) un modèle géométrique de multiplication (3) développé par Hilbert (4) Puisque, d'après E. Barbin, les limites du discours de la nécessité et de la graphie algébrique sont... le mouvement, je décris ci-après ce modèle au moyen du texte d'une figure Géoplan 2 !! (5)

Position de Roxy: Xmin: -11.919245077, Xmax: 11.919245077, Ymax: 11.919245077
Objet dessinable Roxy, particularités: rouge, dessiné

I point de coordonnées (1,0) dans le repère Roxy
J point de coordonnées (0,1) dans le repère Roxy
M point libre sur la droite (oI)
Objet libre M, paramètre: 2.0511129196
N point libre sur la droite (oJ)
Objet libre N, paramètre: -3.0766693793
P projeté de N sur ox parallèlement à (MJ)

Hauteur de la zone des affichages: 50
Af0 affichage des coordonnées du point M (repère Roxy) (6 décimales)
   Position de l'affichage Af0: (30,1)
Af1 affichage des coordonnées du point N (repère Roxy) (6 décimales)
   Position de l'affichage Af1: (3,17)
Af2 affichage des coordonnées du point P (repère Roxy) (6 décimales)
   Position de l'affichage Af2: (29,31)

Commentaire
Si le point M, libre sur l'axe des abcisses, a pour abscisse x,
Si le point N, libre sur l'axe des ordonnées, a pour ordonnée y,
Alors le point P, a pour abscisse x*y, ce que permet de
"vérifier" la ligne d'affichage
Fin de la figure

La pulsation, pour ce que j'en ai compris, est une sorte d'état du mathématicien au travail qui consiste en :
- le refus de se poser la fausse question de la vraie définition ;
- l'acceptation de toutes les types d'évidences, sans en privilégier un en particulier ;
- le geste qui consiste à savoir passer de l'une à l'autre, en rigueur.

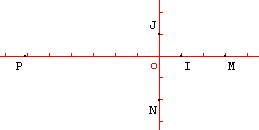
Mais on ne peut s'en contenter : en effet, l'écran de l'ordinateur, toute comme la feuille de papier, ont une surface finie, il est impossible de déplacer les points M et N à une distance aussi grande que l'on veut de O. Dans ces conditions, comment peut-on s'assurer de la vadilité de la propriété énoncée en 1) pour tous nombres réels x et y?

Il faut faire appel à l'évidence algébrique qui permet précisément de dire ce que l'on ne peut voir sur la figure : appelons a l'abscisse de M, b l'ordonnée de N, l'ordonnée de P est-elle a*b quelles que soient les valeurs de a et b ? Comment le démontrer? C'est-à-dire : comment se convaincre que c'est évident?

Il suffit de :
1) trouver l'équation de la droite (JM) : il y a deux cas, suivant que, (JM) est, ou n'est pas parallèle à l'axe des ordonnées :

1.1 (JM) n'est pas parallèle à l'axe des ordonnées (soit a non nul) : on trouve y = -1/a * x + 1
1.2 (JM) n'est pas parallèle à l'axe des ordonnées (soit a nul) : on trouve x = 0

2) trouver l'équation de la parallèle d à (JM) passant par N. Il y a deux cas, qui correspondent aux précédents :

2.1 on a dans ce cas une équation de la forme y = -1/a * x + b
2.2 on a dans ce cas une équation de la forme x = 0

3) de trouver l'abscisse z du P, intersection de d avec l'axe des abscisses, donc :

3.1 on a dans ce cas, on aura donc 0 = -1/a * z + b d'où z = a*b, CQFD
3.2 on a dans ce cas, on aura donc z=0, CQFD

Une notion vouée aux gémonies par les instructions officielles comme la valeur absolue, que l'on n'est a priori pas tenu d'approfondir peut être le lieu d'une activité mathématique véritable, s'appuyant sur un ensemble assez varié de notions du programme (configuration, triangles isométriques, équations de droites, systèmes).

On s'est même servi de Géoplan 2. C'est là le recours à l'évidence technologique, que l'on ne doit pas négliger, à condition, au préalable, de dénoncer cette escroquerie : un ordinateur étant, en dernier ressort, une machine effectuant des opérations sur des 0 et de 1, les logiciels dits de Géométrie ne font probablement pas de Géométrie : ils font de l'Arithmétique (en base 2 plus précisément) et de l'Algèbre. Il n'y a pas de points libres ; il y a des points dont les abscisses et les ordonnées sont paramétrées (la lecture du texte des figures le montre) et peuvent être modifiés par l'action de l'utilisateur. Mais c'est bien, en dernier ressort, sur les abscisses et les ordonnées des points que le programme opère lorsqu'on soumet le texte de la figure donnée en 2).

Ainsi, je ne crois pas qu'on puisse parler d'un avantage de la technologie "Géoplan 2" sur la technologie "papier-crayon". On doit plutôt parler de l'avantage qu'a une personne qui possède de l'Algèbre et de la Géométrie sur une personne qui ne possèderait que l'une des deux... (6)

(1) Lire à ce propos Frédéric Patras, La pensée mathématique contemporaine, collection Science, histoire et société, P. U. F., août 2001. Résumé au dos du livre :

Fruit de la science du XIXème siècle, canon des savoirs ou idéologie sujette à caution, le structuralisme mathématique, après avoir longtemps imposé ses vues jusque dans les sciences humaines, doit aujourd'hui céder la place. La succession est difficile, mais c'est dans ce renouveau nécessaire de la pensée mathématique que se joue sa légitimité intellectuelle et sociale.
Pour comprendre le cheminement de la mathématique contemporaine, son affranchissement progressif des mots d'ordre des"maths modernes", et les voies qui lui sont aujourd'hui ouvertes, il faut d'abord déconstruire une histoire officielle par trop réductrice. Au XIXème siècle, et jusqu'au milieu du XXème, dans les travaux de mathématiciens comme Galois, Hilbert ou Weyl, s'est jouée et affirmée une autre conception de la pensée mathématique. C'est cette tradition de pensée et son exigence philosophique,tradition de savants, non de scientifiques, que la modernité nous apprend à faire revivre au travers d'oeuvres comme celle d'Alexandre Grothendieck ou dans l'aristotélisme d'un René Thom.Retour au texte

(2) On ne progresse que sur un acquis, accepté avec humilité. Reformuler ce qui l'a déjà été, c'est perdre beaucoup de temps ; brûler les anciens ou seulement les ignorer, c'est faire du surplace sinon régresser,écrit C. Ouzilou dans "Dyslexie, une vraie-fausse épidémie". Dans cet état d'esprit, j'en profite pour rappeler qu'il existe un excellent livre de George Polya, écrit en 1951, qui s'appelle "Comment poser et résoudre un problème?", et qui comporte un dictionnaire d'heuristique avec une entrée "Pourquoi des preuves?" (ou l'on reparle d'ailleurs de la configuration de la somme des angles d'un triangle donnée en I.1.1) qui peut aider beaucoup à répondre à cette question lorsqu'elle est, légitimement, posée par des élèves. Légitimement, puisqu'on y apprendra que... le jeune Newton lui-même... se la posait! Retour au texte

(3) Je remercie Michel Delord, qui m'a communiqué son existence... Retour au texte

(4) David Hilbert, Les principes fondamentaux de la Géométrie, Gauthier-Villars, 1900, traduit par L. Laugel (en particulier le paragraphe 26 du Chapitre 5) dont on trouve une version téléchargeable sur le site de la Bibliothèque Nationale de France http://www.gallica.bnf.fr On notera également la citation qui est mise en exergue de l'introduction, à savoir : "Toute science humaine commence par les intuitions, de là passe aux notions, et finit par les idées" (E. Kant, Critique de la raison pure, Partie II, Section II),qui atteste clairement que Hilbert (dont se sont réclamés certains fondateurs du groupe Bourbaki) avait une conception des mathématiques qui ne les limitait pas à un jeu axiomatico-formel. Pour plus de détails, je renvoie à la référence donnée dans la note (1) infra. Retour au texte

(6) Un mathématicien comme René Thom s'est indigné de la disparition de l'enseignement de la Géométrie lors de la mise en oeuvre de la réforme des mathématiques modernes :
Reste que, de toute manière, le problème de géométrie exige beaucoup de temps, d'efforts, une réflexion soutenue, des capacités combinatoires dont peu d'élèves sont capables. Peut-être la géométrie euclidienne est-elle, comme la version latine, un de ces exercices nobles et désuets, réservés à une élite, et incompatibles avec un enseignement de masse. Si tel était le cas, alors l'éviction de la géométrie serait essentiellement un problème sociologique que je préférerais ne pas discuter.
(R. Thom, Les mathématiques modernes, une erreur pédagogique et philosophique ?, L’Age de la science, juillet 1970),
Aussi dans les débats actuels, certains voudraient-ils la voir réhabilitée. Mais, dit F. Patras, il faut faire preuve de nuance :
La revendication d'une fidélité inconditionnelle aux origines qui pourrait naître de l'irritation provoquée par des niveaux d'abstraction successifs dans l'enseignement des mathématiques est dangereuse. Quel sens cela aurait-il aujourd'hui d'enseigner la géométrie euclidienne en faisant l'impasse des aspects algébriques? (Voir note (1) infra, page 28 de l'ouvrage cité)
on ne peut donc pas faire comme si ce que le structuralisme a apporté de meilleur n'avait jamais existé. Retour au texte