Dans, ce texte, je voudrais faire quelques remarques à propos du texte de Ralph A. Raimi que nous avons traduit avec Virginie Jaussaud : "Pourquoi apprendre la trigonométrie?" (http://www.sauv.net/raimi.php), et en déduire, sur le présent titre un peu provocateur, une manière d'introduire au sujet différente de celle que l'on rencontre dans les manuels actuels.

Les remarques concernent plus particulièrement le passage que je recopie ci-après, pour le confort du lecteur :

Mon père était une espèce de menuisier amateur ; en tant que petit entrepreneur, il fabriquait souvent des objetspour son magasin : des rayonnages, des comptoirs, des étalages de vitrine. Un jour, alors qu'il avait déjà atteintsoixante ans, il porta à ma connaissance l'observation suivante :

En fabriquant une pièce verticale pour un jeu de rayonnages, il dut soutenir un des montants avec un étai en bois,en clouant une de ses extrémités au sol à environ trente centimètres de la base du montant, et posant l'autre surla planche verticale. L'étai n'était pas nécessairement à un angle de 45 degrés, mais dépendait de certainesrestrictions du reste de la structure.

Lorsqu'il plaça l'extrémité libre à un point distant du sol de 20 cm, m'expliqua-t-il, l'étai devait évidemment être pluslong que la ligne au sol (la distance au sol entre la base de l'étagère et l'extrémité clouée, NDT) : environ 5 cm de plusque cette dernière, estimait-il. Mais lorsqu'il souhaita placer l'extrémité libre à une distance deux fois plus grande du
sol (c'est-à-dire à 40 cm), il dut ajouter à la longueur de ce deuxième étai plus de deux fois ce qu'il avait ajouté au premier. Il évaluait cette nouvelle longueur à environ 50 cm, soit 20 cm deplus que la ligne au sol, et non 10 cm de plus comme il s'y attendait après en avoir placé l'extrémité à une hauteurdouble de  la première. Pourquoi ? Son langage n'avait rien de technique, mais il constatait que la longueur d'unediagonale ne croit pas de manière proportionnelle à la hauteur.

Il est vrai qu'il ne s'agissait pas vraiment d'un problème pratique, bien que tout ait commencé avec la menuiserie. Iln'éprouva jamais de difficulté au cours de sa vie à effectuer des schémas à l'échelle et à découper son bois en  respectantces derniers. Il n'avait jamais entendu parler de la trigonométrie. Mais, âgé de 60 ans, il était là... saisi  de curiosité àpropos d'un phénomène qu'il n'avait jamais analysé.

Comment se fait-il qu'en concevant un étai appuyé sur un montant à une hauteur de 40 cm, il faut ajouter à la longueur de la ligne au sol plus de deux fois ce que l'on y avait déjà ajouté pour concevoir un premier étai appuyé  à20 cm du sol ?

Evidemment, sa découverte (si on peut dire) était celle du comportement de la cosécante de l'angle que faisait  son étaiavec le sol. Plus simplement, il avait pu observer la concrétisation du théorème de Pythagore, pour laquelle mêmesans recourir aux mesures d'angles on peut constater les écarts dans les proportions quand la  hauteur croît.

Le passage montre un exemple réel de "découverte", en tant qu'elle est involontaire et fortuite, et il est intéressant de remarquer que ce qui est découvert, cela n'est aucune des fonctions des trois fonctions de base enseignées aujourd'hui en collège et lycée, à savoir cosinus, sinus, tangente, mais bien la fonction cosécante, tombée aux oubliettes, dont on doit aller chercher une définition dans un dictionnaire de mathématiques.

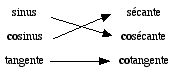
Il y a six fonctions trigonométriques que l'on peut définir : le sinus, le cosinus, la tangente, la cotangente, la sécante et la cosécante. On remarque qu'on a d'un côté les trois fonctions dont les noms sont, sinus, sécante, tangente, et d'un autre côté, les fonctions dont les noms sont obtenus par adjonction du préfixe "co" : dès lors, nul doute qu'une approche interdisciplinaire de l'enseignement de la trigonométrie devrait tenir compte de cet aspect des choses.

Je m'en tiendrai ici à une approche mathématique. Comme on l'a dit plus haut, il faut commencer par chercher les mots, aujourd'hui inconnus, dans le dictionnaire :

Cotangente d'un angle : inverse de la tangente de cet angle.
Sécante d'un angle : inverse du cosinus de cet angle.
Cosécante d'un angle : inverse du sinus de cet angle.

Ainsi cet étalage permet-il de constater, qu'en général, la cofonction n'est pas l'inverse de la fonction : cela n'est vrai que pour la tangente. Néanmoins, on peut se faire le diagramme suivant, avec, sur la colonne de gauche, les fonctions aujoud'hui introduites au collège et au lycée, sur la colonne de gauche, les fonctions inconnues (c'est-à-dire non introduites systématiquement) des lycéens, et des flèches qu'on peut lire : "a pour inverse la fonction" (on se place sur le plus grand ensemble de nombres sur lesquelles toutes ces fonctions sont toujours définies et non nulles, de sorte que l'inversion est toujours possible). Ainsi lira-t-on, dans le diagramme ci-dessous "la fonction sinus a pour inverse la fonction cosécante"
 
 

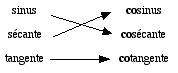
Ce qui est mieux, et permet d'avancer vers la raison du choix judicieux du préfixe "co" : en utilisant les fonctions du membre de gauche, je peux écrire l'égalité :

tangente = sinus x sécante . (1)

En prenant l'inverse des deux membres, j'obtiens :

cotangente = cosécante x cosinus ,

soit :

cotangente =  cosinus x cosécante , (2)

et on voit que je suis passé de l'égalité (1) à l'égalité (2) en remplaçant les fonctions par leurs cofonctions. De sorte que, du point de vue du résultat, inverser l'égalité (1) entre les fonctions , donne l'égalité (2) entre les cofonctions. Ce n'est pas encore suffisant, mais je peux déjà apporter une réponse à la question posée dans le titre : comment enseigner la trigonométrie?

L'approche bourbakiste, qui consiste à ne définir que ce qui est nécessaire, jointe à la volonté d'alléger les programmes, ont fait que le cours de trigonométrie du lycée s'est réduit comme peau de chagrin aux fonctions sinus et cosinus, et à la fonction tangente qui est quotient de ces deux fonctions. Mais on voit bien qu'en occultant les autres fonctions, deux inconvénients se présentent :

- on perd de la richesse en possibilité d'instruction (1) ;

- on rate une définition de la tangente comme produit des fonctions sinus et sécante, fort utile si les divisions ne sont plus apprises à l'école primaire! (2)

On ne peut alors que trouver normal que l'élève qui ne dispose que du sinus et du cosinus, n'ait pas envie de faire autre chose que prendre la tangente... en désertant les études scientifiques.

Question : serait-il convenable de parler d'abord des fonctions, sinus, sécante, tangente, puis des fonctions cosinus, cosécante, cotangente?  Ce qui est sûr, c'est que dans la quatrième édition des  Eléments de Trigonométrie de Frère-Gabriel Marie, publiés en 1890, réédités par la maison Jacques Gabay (http://www.gabay.com/), en 1997, le cours est comme suit :

Chap 1 DES LIGNES TRIGONOMETRIQUES

I - Notions préliminaires
1. La Trigonométrie est la partie des mathématiques qui a pour objet spécial la résolution des triangles par le calcul ...
2. Mesure des angles
3. Variations des arcs et des angles
4. Arcs de même origine et de même extrémité
5. Arcs complémentaires
6. Arcs supplémentaires

II - Des fonctions circulaires.

7. Définitions. Comme il est difficile d'introduire les angles dans le calcul, on a imaginé des les remplacer par des quantités qui en dépendent, et que l'on appelées fonctions circulaires.

La Trigonométrie, dans son acception générale, doit être définie : la partie des mathématiques qui a pour objet l'étude des fonctions circulaires.

Ces fonctions, que l'on appelle aussi rapports trigonométriques, sont au nombre de six, savoir : le sinus, la tangente, la sécante, le cosinus, la cotangente et la cosécante. (On écrit, pour abréger : sin, tg, séc, cos, cotg, coséc.)

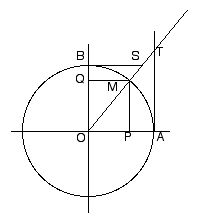
On appelle SINUS d'un arc le rapport au rayon de la perpendiculaire abaissée de l'extrémité de cet arc sur le diamètre qui passe par l'origine. Ainsi le rapport

MP
---- est le sinus de l'arc AM ou de l'angle AOM.
OA

On appelle TANGENTE d'un arc le rapport au rayon de la perpendiculaire élevée à l'extrémité du rayon mené par l'origine, jusqu'à la rencontre du rayon prolongé qui passe par l'extrémité de cet arc.

AT
----  est la tangente de l'arc AM ou de l'angle AOM.
OA

On appelle SECANTE le rapport au rayon de la droite qui joint le centre à l'extrémité de la tangente.

OT
----  est la sécante de l'arc AM ou de l'angle AOM.
OA

Le rayon étant pris pour unité, les rapports que nous venons de considérer se réduisent aux nombres qui mesurent leurs numérateurs ; MP est alors le sinus de l'arc AM, AT en est la tangente, et OT la sécante. Ces longueurs MP, AT, et OP sont appelées les lignes trigonométriques de l'arc AM, et les définitions qui précèdent peuvent être remplacées par les suivantes :

Lignes trigonométriques. On appelle sinus d'un arc la perpendiculaire abaissée de l'extrémité de cet arc sur le diamètre qui passe par l'origine.
On appelle tangente la perpendiculaire élevée à l'extrémité du rayon qui passe par l'origine, jusqu'à la rencontre du rayon prolongé qui passe par l'extrémité de l'arc.
On appelle sécante la ligne qui joint le centre à l'extrémité de la tangente.
On appelle cosinus, cotangente, et cosécante d'un arc, le sinus, la tangente, et la sécante du complément de cet arc ; ces fonctions sont désignés sous le nom de fonctions complémentaires

ce qui sonne mieux que "cofonctions", néologisme formé ci-dessus par moi! L'auteur ajoute :

Ainsi l'arc AM, ayant pour complément BM a pour cosinus MQ, pour cotangente BS, et pour cosécante OS.

Moralité :

a) Il en va du cours de trigonométrie comme des transats en solitaire : le chemin le plus court (du point de vue de la formulation des énoncés) n'est pas le plus rapide (pour la compréhension) : il faut tenir compte de la force des vents ; en conséquence :

b) "Nous devons travailler dans l'universel et dans la lenteur", comme je m'en faisais l'écho dans "Quelles sont les obstacles à l'enseignement  des mathématiques au lycée?" (http://www.sauv.net/ensmath1.php) ; autre façon de le dire :

c) "Le moyen d'avoir raison dans l'avenir, est, à certaines heures, de savoir se résigner à être démodé" (Ernest Renan, Qu'est-ce qu'une nation, 1889, cité dans Sauver les lettres -- des professeurs accusent, 2001, http://www.sauv.net/sll.php3)

(1) A  mon sens, l'enseignement doit être vaste, parce qu'il ne s'agit pas d'apprendre des recettes, il n'est pas question de par-coeur, mais de réflexion et de savoir-faire par soi-même. Or on ne peut pas vraiment réfléchir sur rien ou sur peu, il faut précisément pourvoir se mettre à agir dans un réseau suffisamment riche, croiser des conceptions, en utiliser plusieurs en même temps, en distinguer, en confondre. Les gymnastiques d'entraînement local, indispensables doivent pouvoir aussi être ensuite pensées, estimées, comparées. Sans la mise à disposition d'un "savoir" relativement important, il n'est plus question que d'un travail de singe (que je ne méprise pas, qu'il faut pleinement, nécessairement, mais ce n'est jamais suffisant), et le propre de l'activité du mathématicien n'est pas enseigné (René Guitart, La pulsation mathématique, L'Harmattan, 1999, no 42, SEPARATION DES GENRES "INSTRUIRE" ET "SANCTIONNER") A mon sens aussi, est-il utile de le préciser. Retour

(2) Je suis ici bien sûr d'une totale mauvaise foi, comme le lecteur attentif le remarquera en lisant la suite, puisque les trois fonctions, sinus, sécante, tangente, sont définies elles comme des quotients de longueurs!Retour