TITRES ET RESUMES DES CONFERENCES
 
 


E. Amar (Université Paris 13)
Interaction de deux résonances en dimension un pour l'opérateur de Schrödinger

On considère un opérateur de Schrödinger semi-classique P=-h²(delta)+V(x), en dimension un. Le potentiel V est analytique dans un secteur, ce qui permet de définir les résonances par dilatation analytique. Il présente deux puits et une mer près des niveaux d'énergies considérés, supposés loin des valeurs critiques de V. On sait qu'il existe alors des résonances associées à chaque puits données par des conditions de quantification. On étudie ici ce qui se passe lorsque deux résonances associées à chacun des deux puits peuvent être très proches (il y a interaction). On obtient en particulier des résultats précis sur les parties imaginaires des résonances. Pour cela, on construit des solutions exactes de Pu=Eu suivant la méthode de [Buslaev-Grigis] pour l'opérateur de Stark-Wannier. On obtient une condition de quantification exacte, et une étude détaillée de cette équation nous donne le résultat.



J. Bellissard (Université Paul Sabatier, Toulouse & Institut Universitaire de France)

Exposants fractals et transport anormal pour les opérateurs de Schrödinger en milieux apériodiques

Dans un milieu apériodique, l'opérateur de Schrödinger décrivant le mouvement électronique, dans l'approximation des électrons indépendants, est une famille covariante fortement continue (au sens des résolvantes) d'opérateurs auto-adjoints. Les exposants spectraux permettent de définir la classe de regularité locale des mesures spectrales utiles (densité d'états ou DOS, densité d'états locale ou LDOS). Certains de ces exposants sont des invariants de la classe des mesures considérées, tandis que d'autres, comme les exposants multi-fractals, ne le sont pas. Par ailleurs, le comportement dynamique des paquets d'onde soumis à l'évolution donnée par un tel opérateur, est caratérisé par un exposant de transport dont on donnera la définition. Diverses inégalités, dérivant de l'inégalité de Guarneri (1989), seront fournies. Des résultats récents permettent de donner des exemples d'opérateurs à spectre absolument continu, à dynamique sous-diffusive en dimension 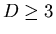, et pour lesquel ces inégalités sont saturées. Dans le cas des modèles de type Harper, décrivant les électrons 2D en champ magnétique fort, de nouvelles inégalités, numériquement optimale, ont été démontrées. Enfin, on discutera la pertinence de ces inégalités pour la Physique du Solide, au travers de la formule de Drude anormale pour la conductivité dans l'approximation de temps de relaxation.

O. Bourget (Grenoble)

Spectre d'opérateurs de Floquet aléatoires

Nous étudions le spectre d'une famille aléatoire d'opérateurs unitaires issu d'un modèle de conduction électronique. Notre approche généralise les constructions effectuées pour les matrices de Jacobi aléatoires. Nous montrons l'absence générique de spectre absolument continu.



A. M. Boutet de Monvel (Université Paris 7)

Localization for continuum random surface models

We prove Anderson localization and strong dynamical localization for some random surface models in R^d. These models exhibit a metalinsulator transition. We establish localization, i.e. suppresion of transport, near the bottom of the spectrum. The method of proof is multiscale analysis.



E.B. Davies (King's college, Londres)

Spectral theory of non-self-adjoint elliptic systems

We describe the spectrum of a non-self-adjoint elliptic system on a finite interval. Under certain conditions we find that the eigenvalues form a discrete set and converge asymptotically at infinity to one of several straight lines. The eigenfunctions need not generate a basis of the relevant Hilbert space, and the larger eigenvalues are extremely sensitive to small perturbations of the operator. We show that the leading term in the spectral asymptotics is closely related to a certain convex polygon, and that the spectrum does not determine the operator up to similarity. Two elliptic systems which only differ in their boundary conditions may have entirely different spectral asymptotics.

J. Derezinski (Varsovie, Pologne)

Perturbation theory of Liouvilleans and KMS states

Suppose we are given a W^*-algebra equipped with a W^*-dynamics and a KMS state. Such systems arise naturally in the study of infinitely extended quantum sysytems in equilibrium. I will describe recent results due to V. Jaksic and C.A. Pillet concerning stability of such systems with respect to unbounded perturbations. I will also discuss various definitions of the so-called Liouvillean.

F. Faure (Grenoble)

Indices topologiques dans les spectres moléculaires

L'approximation de Born-Oppenheimer peut etre appliquée lorsqu'un système quantique est couplé à un autre système comparativement plus lent que l'on traite classiquement. C'est par exemple le cas du couplage vibration-rotation dans certaines petites molécules. Cette situation se manifeste dans le spectre d'énergie exact par un regroupement des valeurs propres d'énergie en petits groupes que l'on appelle des "bandes". Par une approche semi-classique, on montre que le nombre exact de valeurs propres dans chaque bande s'exprime par la formule de l'indice d'Atiyah-Singer, à l'aide d'indices topologiques associés à un fibré vectoriel, que l'on calcule dans l'approximation de Born-Oppenheimer. La modification de ces indices topologiques est associée à des sous variétés de dégénérescence et à l'échange de niveaux entre bandes consécutives. Cela est illustré sur des exemples très simples.



A. Grigis (Université Paris 13)
Interaction pour les résonances de Stark-Wannier

Cet exposé est dans la suite du programme de recherche entrepris avec V.Buslaev sur l'existence et la localisation des résonances de Stark-Wannier. Nous considérons le cas d'un potentiel périodique générique c'est-à-dire pour lequel le spectre de l'équation de Hill associée a une infinité de gaps ouverts. Pour une énergie donnée l'hamiltonien effectif associé présente alors une infinité de puits et ceux-ci rentrent en interaction. Nous arrivons tout de même à prouver l'existence de résonances de Stark-Wannier et à donner une estimation sur leurs parties imaginaires.



F. Germinet (Université Lille I (USTL))

Caractérisation de la transition métal-isolant d'Anderson

La transition métal-isolant dans les modèles d'Anderson est généralement interprétée comme une transition de type spectrale. Si l'existence d'une telle transition semble toujours hors de portée, sa nature même l'est tout autant: transition pp/ac, transition pp/sc/ac, cohabitation de spectres de differentes natures ? Dans ce travail nous recentrons notre attention sur les propriétés de transport du modèle d'Anderson et redéfinissons la transition en termes dynamiques. Nous montrons alors que les exposants de transports permettent de caractériser une telle transition. Nous démontrons pour cela que la region des énergies où les exposants de transport sont nuls correspond exactement à la région où règne la localisation dynamique forte. En particulier nous montrons que l'analyse multi-échelle fonctionne jusqu'au seuil de transition. De plus nous démontrons que s'il y a transition, alors les exposants de transport doivent être discontinus en ce point, et nous fournissons une valeur minimal pour ce saut (ce travail fait l'objet d'une collaboration avec A. Klein, U.C. Irvine).



G.M. Graf (Zürich, Suisse)

Quantum pumps

Quantum pumps are devices (typically realized as semiconductor quantum dots) generating currents between two or more electrodes as a result of being operated parametrically. I will discuss adiabatic quantum pumps on time scales that are short relative to the cycle of the pump. In this regime the pump is characterized by the matrix of energy shift which we introduce as the dual to Wigner's time delay. The energy shift determines the charge transport (first computed by Buettiker et al.), the dissipation, the noise and the entropy production. I will present a general lower bound on dissipation in a quantum channel and define optimal pumps as those that saturate the bound. There is a geometric characterization of optimal pumps which shows that they are noiseless and transport integral charge in a cycle. Finally I will give an example of an optimal pump related to the Hall effect. These results are based on joint work with J. Avron, A. Elgart, L. Sadun.

D. Hafner (Université Bordeaux1)

Sur la theorie de la diffusion pour l'equation de Klein-Gordon dans la metrique de Kerr

Nous démontrons la complétude asymptotique pour l'équation de Klein-Gordon dans la métrique de Kerr après restriction à certains espaces de solutions d'énergie positive. Nous comparons la dynamique de Klein-Gordon avec la dynamique libre près de l'horizon du trou noir et avec une dynamique modifiée de type Dollard a l'infini.



M. Holschneider (Postdam, Allemagne)
Diffusion through time dependent media: a possible explanation for the Abaratsubo co-seismic events?

Coseismic resistivity changes observed near Abaratsubo (Japan) show a clear seasonal polarity. We propose a model based on time-dependent diffusion coefficients for the saturation to explain the observations. The mathematical analysis gives an assymptotic development of the solution of the heat equation in a half-space near the boundary for short durations of the perturbation. It is shown that jumps of the size of the average perturbation may occur.



A. Joye (Grenoble)

Transport magnétique dans un guide d'ondes quantique rectiligne

On considère un electron quantique bi-dimensionnel en champ magnétique homogène confiné par un potentiel parabolique en une variable, figurant un guide d'ondes rectiligne. On s'intéresse aux propriétés spectrales de ce système lorsqu'il est soumis à un potentiel perturbatif W. Lorsque W est périodique dans la direction libre, on donne des conditions assurant l'absolue continuité du spectre ou du bas du spectre et un nombre arbitraire de gaps. Lorsque W est petit et satisfait une condition de localisation faible dans la direction libre, on construit un opérateur conjugué au sens de Mourre assurant l'absolue continuité de certaines parties du spectre.



D. Krejcirik (Université de Reims)

Guides d'ondes quantiques sur les surfaces

On considère une particule quantique dans le guide d'ondes courbé produit sur une surface. On introduit l'hamiltonien de ce système comme étant le laplacien Dirichlet dans un voisinage tubulaire d'une courbe infinie sur la surface et on étudie les propriétés spectrales de cet opérateur. En particulier, on énonce des hypothèses sous lesquelles l'hamiltonien possède des états liés au-dessous du spectre essentiel. Les guides d'ondes construits sur les surfaces à courbure positive sont analysés en détail; on déduit de ce cas général les résultats connus pour les guides d'ondes dans le plan et on présentera un exemple non trivial.



P. Leboeuf (Paris Sud)

Corrélations quantiques, résonances classiques et la fonction zêta de Riemann

Pour des distances de l'ordre de l'espacement moyen entre niveaux, il est bien connu que les corrélations spectrales des systèmes classiquement chaotiques obéissent à la théorie des matrices aléatoires. Sur des plus grandes distances elles ne s'annulent pas, et sont contrôlées par les orbites périodiques courtes. Nous montrerons comment les corrélations peuvent être exprimées en fonction des résonances classiques liées à l'opérateur de Perron-Frobenius. Cette connexion permet de mettre en évidence une propriété remarquable des zéros complexes de la fonction zêta de Riemann: les corrélations de longue portée entre des zéros très éloignés de l'axe réel sont contrôlées par les zéros proches de cet axe. Cette propriété de "resurgence" produit une structure hiérarchique autosimilaire dont les ingrédients principaux seront détaillés.



G. Nenciu (Bucarest, Roumanie)

Resolvent expansions at thresholds revisited
Joint results with A. Jensen concerning resolvent expansions at thresholds are presented. Although the method used is quite general ( actually it can be put in an abstract form), for definiteness we consider the case of resolvent expansion around zero energy for standard Schrodinger operator with sufficiently rapidly decaying potential. The approach is working in all dimensions and in dimensions one and two does not require to distinguish whether the mean value of the potential vanishes or not.



G. Raikov (Santiago, Chili)

Eigenvalue Distribution for the Perturbed Pauli Operator with Periodic Magnetic Field

I will discuss the asymptotics of the negative discrete eigenvalues for the two-dimensional Pauli operator H with periodic magnetic field B, perturbed by a scalar potential V which decays at infinity.

Two different types of asymptotic distribution of the discrete spectrum will be established; they correspond to the cases of zero and non-zero flux of B respectively. In the case where the flux does not vanish, I will also talk about the asymptotics of the eigenvalues of H situated in the first spectral gap of the unperturbed operator, and accumulating to the origin from the right.

Some of the results are obtained in collaboration with M.Dimassi (University of Paris 13).



D. Robert (Nantes)

Que se passe-t-il au voisinage du temps de Ehrenfest?

Il s'agit d'un travail en collaboration avec S. Debièvre (Université de Lille). On étudie l'évolution quantique des valeurs moyennes d'un état cohérent centré à l'instant initial sur un point d'équilibre instable pour un potentiel présentant des puits multiples. Nous montrons que pour des temps de l'ordre de 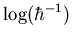l'état cohérent se scinde en deux morceaux localisés sur les points d'équilibre instables voisins. De plus on met en évidence l'existence d'un régime transitoire durant lequel l'état cohérent est localisé le long de la trajectoire classique joignant deux points d'équilibre instables, suivant une densité que l'on peut calculer.



R. Schubert (CEA Saclay)

Semiclassical localization in phase space

We study semiclassical properties of quantum systems whose classical limit is neither chaotic nor integrable. The phase space of the corresponding classical systems possess plenty of invariant sets, and we construct approximate projection operators associated with open invariant sets as Anti-Wick quantizations of their characteristic functions. Under an additional condition on the invariant set, called stable invariance, the construction yields approximate projection operators whose commutator with the Hamilton operator is bounded by any power of 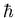. This generalizes previous results of Shnirelman (1993). Finally, we discuss some applications to time evolution and quasimodes.