


Next: About this document ...
Université Bordeaux I -- IUFM d'Aquitaine
A. Hartmann
Mathématiques CAPET Techno 2008
Feuille 1 - Nombres complexes, fonctions numériques
(L'essentiel des exercices ci-après
est extrait du manuel Mathématiques, Spécialités du
groupement A, Nathan Technique, 2002.)
Pour me contacter : Andreas.Hartmann@math.u-bordeaux1.fr
Les corrigés de ces feuilles seront ultérieurement mis à disposition
à l'adresse :
http://www.math.u-bordeaux.fr/~ hartmann/ENSEIGNEMENTS/capet2008.html
Nombres complexes
Exercice 1. Ecrire sous la forme algébrique 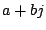 , les nombres
complexes :
a)
, les nombres
complexes :
a)
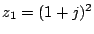 ,
,
b)
 ,
c)
,
c)
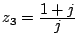 ,
d)
,
d)
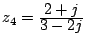 .
.
Exercice 2. Donner le module et un argument des nombres complexes :
a)
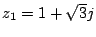 ,
,
b)
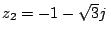 ,
c)
,
c)
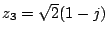 ,
d)
,
d) 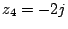 .
.
Exercice 3. Ecrire sous forme algébrique 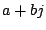 les nombre
complexes de module
les nombre
complexes de module 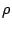 et d'argument
et d'argument 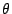 :
:
a) 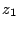 :
: 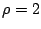 et
et
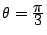 ,
b)
,
b) 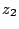 :
:
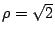 et
et
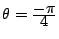 ,
c)
,
c) 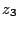 :
: 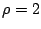 et
et
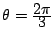 ,
d)
,
d) 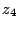 :
: 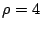 et
et
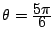 .
.
Exercice 4. Dans un repère orthonormal du plan
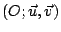 placer les point
placer les point 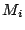 d'affixe
d'affixe 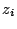 :
a)
:
a) 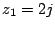 ,
b)
,
b) 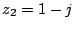 ,
c)
,
c)
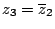 ,
d)
,
d)
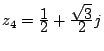 .
.
Exercice 5. Dans 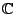 , donner l'ensemble des solutions
des équations :
a)
, donner l'ensemble des solutions
des équations :
a) 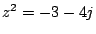 ,
b)
,
b) 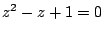 ,
c)
,
c)
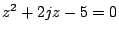 ,
d)
,
d)
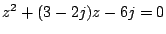 .
.
Exercice 6. Dans 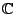 , donner l'ensemble des solutions du
système d'équations
{
, donner l'ensemble des solutions du
système d'équations
{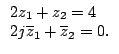 .
Exercice 7. A l'aide des formules d'Euler, retrouver les formules
trigonométriques suivantes :
.
Exercice 7. A l'aide des formules d'Euler, retrouver les formules
trigonométriques suivantes :
a)
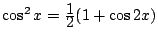 ,
b)
,
b)
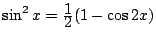 .
.
Exercice 8. A l'aide des formules d'Euler, linéariser :
a)
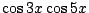 ,
b)
,
b)
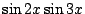 ,
c)
,
c) 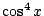 .
.
Exercice 9. Soient
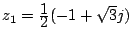 et
et
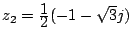 . Comparer
. Comparer 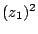 à
à 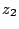 .
Comparer
.
Comparer 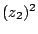 à
à 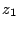 . Calculer
. Calculer 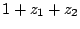 .
.
Exercice 10. Soit 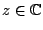 . On pose
. On pose
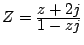 .
.
1. Déterminer les parties réelles et imaginaires de 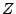 .
.
2. Déterminer l'ensemble des point 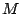 d'affixe
d'affixe 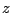 tels que
a)
tels que
a) 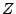 est réel, b)
est réel, b) 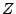 est imaginaire pur.
est imaginaire pur.
Exercice 11. Soient
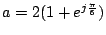 ,
,
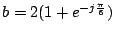 et
et
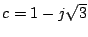 .
.
1. Ecrire 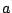 et
et 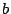 sous forme algébrique.
sous forme algébrique.
2. Le plan complexe est muni d'un repère orthonormal
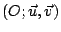 ;
;
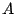 ,
, 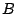 et
et 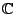 sont les points d'affixe
sont les points d'affixe 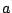 ,
, 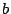 ,
, 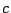 . Donner le module
de
. Donner le module
de 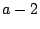 , de
, de 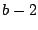 et de
et de 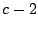 . En déduire que
. En déduire que 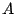 ,
,
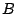 et
et 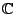 sont sur un même cercle que l'on déterminera.
sont sur un même cercle que l'on déterminera.
3. 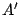 ,
, 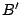 ,
, 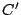 sont les points d'affixe
sont les points d'affixe 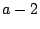 ,
, 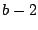 ,
, 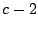 . Par
quelle transformation géométrique passe-t-on de
. Par
quelle transformation géométrique passe-t-on de 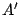 à
à 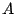 ,
de
,
de 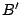 à
à 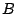 et de
et de 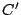 à
à 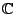 ?
?
4. Déterminer les coordonnées du centre de cercle circonscrit au
triangle 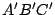 et donner son rayon.
et donner son rayon.
Problème (d'après BTS). La fonction de transfert d'un
filtre, en régime harmonique, peut s'écrire
T(&omega#omega;)=&alpha#alpha;1+ja&omega#omega;1+jb&omega#omega;
où
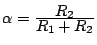 ,
, 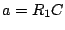 ,
,
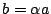 ,
,
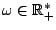 ,
,
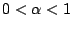 . Ici
. Ici 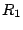 et
et 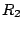 sont les valeurs
(en Ohms) de deux résistors, et
sont les valeurs
(en Ohms) de deux résistors, et 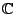 est la capacité (en Farads)
d'un condensateur ; toutes ces valeurs sont donc strictement positives.
est la capacité (en Farads)
d'un condensateur ; toutes ces valeurs sont donc strictement positives.
Le but du problème est d'ajuster 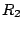 et
et 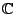 pour obtenir un filtre
dont les propriétés sont fixées connaissant
pour obtenir un filtre
dont les propriétés sont fixées connaissant 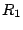 .
.
Partie A.
1. Montrer que pour tout 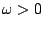 :
T(&omega#omega;)=&alpha#alpha;+(1-&alpha#alpha;)11-j1b&omega#omega;.
:
T(&omega#omega;)=&alpha#alpha;+(1-&alpha#alpha;)11-j1b&omega#omega;.
2. Le plan
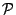 muni d'un repère orthonormal
muni d'un repère orthonormal
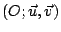 .
Quel est l'ensemble
.
Quel est l'ensemble 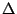 des points
des points 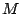 d'affixe
d'affixe
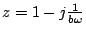 noté
noté
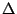 .
.
3. Soit la fonction
f:^*&&C
z&&f(z)=&alpha#alpha;+(1-&alpha#alpha;)1z,
et 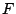 la transformation ponctuelle associée
qui à tout point
la transformation ponctuelle associée
qui à tout point 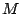 d'affixe
d'affixe 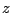 de
de
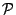 privé de
privé de 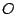 associe le point
associe le point 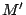 d'affixe
d'affixe 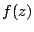 .
.
a. En utilisant les propriétés de la transformation
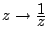 définir l'ensemble
définir l'ensemble 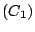 des points
des points 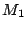 d'affixe
d'affixe
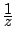 obtenu quand
obtenu quand 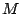 décrit
décrit 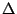 .
.
b. Quelle est la transformation ponctuelle faisant passer de
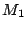 à
à 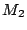 d'affixe
d'affixe
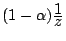 ? En
déduire l'ensemble
? En
déduire l'ensemble 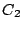 décrit par
décrit par 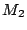 quand
quand 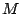 décrit
décrit
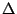 .
.
c. Soit 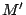 d'affixe
d'affixe
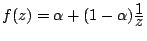 .
Quelle est la transformation ponctuelle faisant passer de
.
Quelle est la transformation ponctuelle faisant passer de
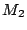 à
à 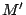 ? En déduire l'ensemble
? En déduire l'ensemble 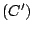 décrit par
décrit par
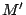 quand
quand 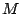 décrit
décrit 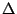 .
.
4. Soit 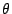 l'argument de
l'argument de 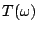 tel que
tel que
![$ \theta\in ]0,\pi/2[$](img91.png) ,
déterminer graphiquement le point
,
déterminer graphiquement le point 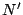 de
de 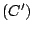 en lequel
en lequel
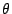 est maximum. On note
est maximum. On note 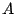 la valeur maximum de cet
argument. Calculer
la valeur maximum de cet
argument. Calculer 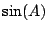 en fonction de
en fonction de 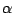 .
.
5. Représenter ces ensembles dans le cas
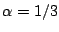 , on prendra
une unité graphique de 9cm.
, on prendra
une unité graphique de 9cm.
Partie B.
Dans cette partie on se propose de calculer les valeurs de 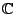 et
de
et
de 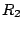 de sorte que
de sorte que 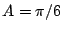 pour une fréquence
de 1kHz.
pour une fréquence
de 1kHz.
1. De 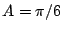 , déduire la valeur correspondante de
, déduire la valeur correspondante de
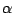 , puis celle de
, puis celle de 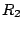 .
.
2. En admettant que
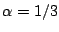 , sur la figure de la partie A, construire
le point
, sur la figure de la partie A, construire
le point 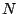 de
de 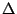 dont l'image par
dont l'image par 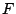 est le point
est le point 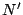 . Calculer
la distance
. Calculer
la distance 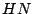 (
(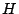 étant le point d'affixe 1). En déduire la
valeur correspondante de
étant le point d'affixe 1). En déduire la
valeur correspondante de 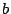 , puis celle de
, puis celle de 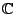 .
.
Fonctions numériques
Exercice 1.
Calculer
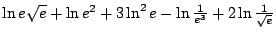 . Exprimer en fonction de
. Exprimer en fonction de 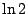 , l'expression
, l'expression
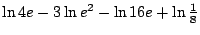 .
.
Exercice 2. Résoudre a)
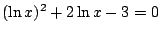 , b)
, b)
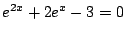 ,
c)
,
c)
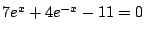 .
.
Exercice 3. Résoudre dans ![$ [0,2\pi]$](img106.png) les équations et
inéquations :
les équations et
inéquations :
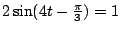 ;
;
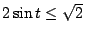 .
.
Exercice 4. Déterminer les limites en 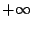 et
et
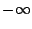 des fonctions définies par
des fonctions définies par
 et
et
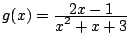 .
.
Exercice 5. Soit 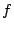 la fonction définie sur
la fonction définie sur 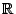 par
par
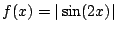 . Montrer que
. Montrer que 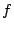 est paire et périodique de période
est paire et périodique de période
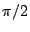 . Etudier les variations de
. Etudier les variations de 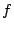 . Donner la représentation
graphique de
. Donner la représentation
graphique de 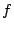 sur
sur
![$ [-\pi,2\pi]$](img117.png) . Etudier la continuité et la
dérivabilité de
. Etudier la continuité et la
dérivabilité de 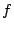 .
.
Exercice 6. Après avoir précisé le (ou les) intervalle(s)
où la fonction est dérivable déterminer dans chaque cas la
fonction dérivée de
a)
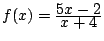 ,
b)
,
b)
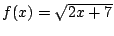 ,
c)
,
c)
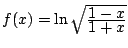 ,
d)
,
d)
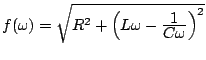 ,
,
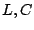 étant des paramètres positifs.
étant des paramètres positifs.
Exercice 8. Après avoir précisé le (ou les) intervalle(s)
où la fonction est dérivable, calculer les dérivées
premières des fonctions 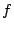 définies par :
a)
définies par :
a)
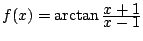 ,
b)
,
b)
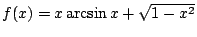 ,
,
c)
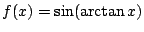 .
.
Problème. Un quadripole composé d'une résistance 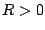 ,
d'une inductance
,
d'une inductance 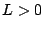 et d'une capacité
et d'une capacité 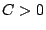 transforme un signal
d'entrée d'une tension alternative
transforme un signal
d'entrée d'une tension alternative 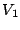 de pulsation
de pulsation 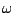 (
(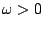 ) en un signal de sortie de tension
) en un signal de sortie de tension 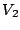 . La fonction
de transfert en régime sinusoïdal est la fonction
. La fonction
de transfert en régime sinusoïdal est la fonction 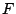 définie sur
définie sur
![$ ]0,+\infty[$](img132.png) par
F(&omega#omega;)=11+jR(C&omega#omega;-1L&omega#omega;).
par
F(&omega#omega;)=11+jR(C&omega#omega;-1L&omega#omega;).
1. On note 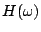 le module de
le module de 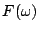 [gain du système].
Montrer que
H(&omega#omega;)=11+R^2(C&omega#omega;-1L&omega#omega;)^2.
[gain du système].
Montrer que
H(&omega#omega;)=11+R^2(C&omega#omega;-1L&omega#omega;)^2.
2. a. Soit 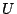 la fonction définie sur
la fonction définie sur
![$ I=]0,+\infty[$](img136.png) par
par
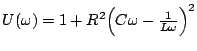 . Montrer que
U'(&omega#omega;)=2R^2L&omega#omega;(C+1L&omega#omega;^2)
(LC&omega#omega;^2-1).
. Montrer que
U'(&omega#omega;)=2R^2L&omega#omega;(C+1L&omega#omega;^2)
(LC&omega#omega;^2-1).
b. En remarquant que
H(&omega#omega;)=1U(&omega#omega;)=[U(&omega#omega;)]^-1/2,
montrer que
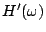 et
et
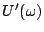 sont de signes contraires.
sont de signes contraires.
c. Etudier les variations de la fonction 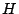 sur
sur 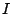 . On précisera
les limites en 0 et en
. On précisera
les limites en 0 et en 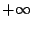 .
.
3. Donner l'allure de la représentation graphique de 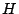 dans un
repère orthonormal.
dans un
repère orthonormal.
4. On note 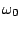 la valeur de pulsation pour laquelle la fonction
la valeur de pulsation pour laquelle la fonction
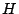 est maximum. On appelle alors pulsation de coupure -3dB toute
valeur de
est maximum. On appelle alors pulsation de coupure -3dB toute
valeur de 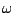 telle que
telle que
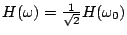 .
Montrer graphiquement que le filtre présente deux pulsations de
coupure
.
Montrer graphiquement que le filtre présente deux pulsations de
coupure 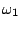 et
et 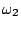 (
(
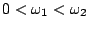 ). Calculer
). Calculer
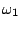 et
et 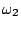 (on pourra se ramener à la résolution
de 2 équations du second degré).
(on pourra se ramener à la résolution
de 2 équations du second degré).
5. L'intervalle
![$ [\omega_1;\omega_2]$](img146.png) est appelé bande passante
du filtre. Déterminer la longueur de la bande passante du filtre.
Seules les fréquences situées dans la bande passante du filtre
sont transmises. Ce filtre est donc appelé un ``filtre passe
bande''.
est appelé bande passante
du filtre. Déterminer la longueur de la bande passante du filtre.
Seules les fréquences situées dans la bande passante du filtre
sont transmises. Ce filtre est donc appelé un ``filtre passe
bande''.



Next: About this document ...
Andreas Hartmann
2007-09-14
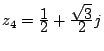 .
.
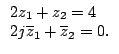 .
Exercice 7. A l'aide des formules d'Euler, retrouver les formules
trigonométriques suivantes :
.
Exercice 7. A l'aide des formules d'Euler, retrouver les formules
trigonométriques suivantes :
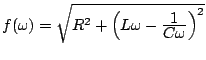 ,
,
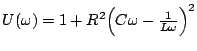 . Montrer que
U'(&omega#omega;)=2R^2L&omega#omega;(C+1L&omega#omega;^2)
(LC&omega#omega;^2-1).
. Montrer que
U'(&omega#omega;)=2R^2L&omega#omega;(C+1L&omega#omega;^2)
(LC&omega#omega;^2-1).