Charles Deledalle - Software
Software
Inverse problems and low-rank matrices
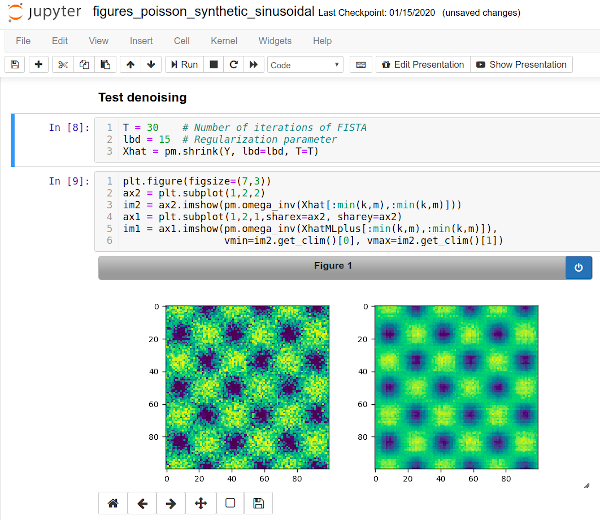
Python open-source software distributed under CeCILL license for low rank matrix denoising for count data. This software is concerned by the analysis of observations organized in a matrix form whose elements are count data assumed to follow a Poisson or a multinomial distribution. We focus on the estimation of either the intensity matrix (Poisson case) or the compositional matrix (multinomial case) that is assumed to have a low rank structure. We propose to construct an estimator minimizing the regularized negative log-likelihood by a nuclear norm penalty. Our approach easily yields a low-rank matrix-valued estimator with positive entries which belongs to the set of row-stochastic matrices in the multinomial case. Then, our main contribution is to propose a data-driven way to select the regularization parameter in the construction of such estimators by minimizing (approximately) unbiased estimates of the Kullback-Leibler (KL) risk in such models. The evaluation of these quantities is a delicate problem, and we introduce novel methods to obtain accurate numerical approximation of such unbiased estimates. Simulated data are used to validate this way of selecting regularizing parameters for low-rank matrix estimation from count data. Examples from a survey study and metagenomics also illustrate the benefits of our approach for real data analysis. |
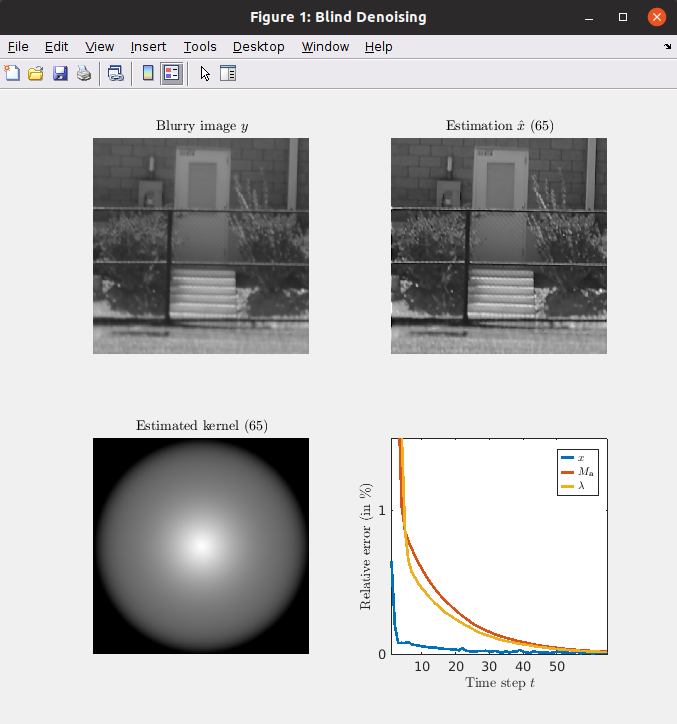
Matlab open-source software distributed under CeCILL license for blind atmospheric turbulence deblurring. A new blind image deconvolution technique is developed for atmospheric turbulence deblurring. The originality of the proposed approach relies on an actual physical model, known as the Fried kernel, that quantifies the impact of the atmospheric turbulence on the optical resolution of images. While the original expression of the Fried kernel can seem cumbersome at first sight, we show that it can be reparameterized in a much simpler form. This simple expression allows us to efficiently embed this kernel in the proposed Blind Atmospheric TUrbulence Deconvolution (BATUD) algorithm. BATUD is an iterative algorithm that alternately performs deconvolution and estimates the Fried kernel by jointly relying on a Gaussian Mixture Model prior of natural image patches and controlling for the square Euclidean norm of the Fried kernel. Numerical experiments show that our proposed blind deconvolution algorithm behaves well in different simulated turbulence scenarios, as well as on real images. Not only BATUD outperforms state-of-the-art approaches used in atmospheric turbulence deconvolution in terms of image quality metrics, but is also faster. |
Matlab open-source software to perform fast image restoration with a GMM prior. Image restoration methods aim to recover the underlying clean image from corrupted observations. The Expected Patch Log-likelihood (EPLL) algorithm is a powerful image restoration method that uses a Gaussian mixture model (GMM) prior on the patches of natural images. Although it is very effective for restoring images, its high runtime complexity makes EPLL ill-suited for most practical applications. In this work, we propose three approximations to the original EPLL algorithm. The resulting algorithm, which we call the fast-EPLL (FEPLL), attains a dramatic speed-up of two orders of magnitude over EPLL while incurring a negligible drop in the restored image quality (less than 0.5 dB). We demonstrate the efficacy and versatility of our algorithm on a number of inverse problems such as denoising, deblurring, super-resolution, inpainting and devignetting. To the best of our knowledge, FEPLL is the first algorithm that can competitively restore a 512x512 pixel image in under 0.5s for all the degradations mentioned above without specialized code optimizations such as CPU parallelization or GPU implementation. |
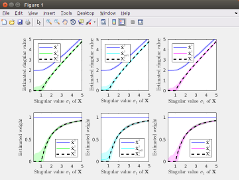
Matlab open-source software distributed under CeCILL license for data driven srhinkage of singular values. We consider the problem of estimating a low-rank signal matrix from noisy measurements under the assumption that the distribution of the data matrix belongs to an exponential family. In this setting, we derive generalized Stein's unbiased risk estimation (SURE) formulas that hold for any spectral estimators which shrink or threshold the singular values of the data matrix. This leads to new data-driven spectral estimators, whose optimality is discussed using tools from random matrix theory and through numerical experiments. Under the spiked population model and in the asymptotic setting where the dimensions of the data matrix are let going to infinity, some theoretical properties of our approach are compared to recent results on asymptotically optimal shrinking rules for Gaussian noise. It also leads to new procedures for singular values shrinkage in finite-dimensional matrix denoising for Gamma-distributed and Poisson-distributed measurements. |
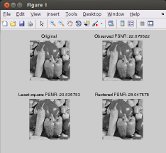
Matlab open-source software for the automatic selection of (multiple) parameters in inverse problems. Algorithms to solve variational regularization of ill-posed inverse problems usually involve operators that depend on a collection of continuous parameters. When these operators enjoy some (local) regularity, these parameters can be selected using the so-called Stein Unbiased Risk Estimate (SURE). While this selection is usually performed by exhaustive search, we address in this work the problem of using the SURE to efficiently optimize for a collection of continuous parameters of the model. When considering non-smooth regularizers, such as the popular l1-norm corresponding to soft-thresholding mapping, the SURE is a discontinuous function of the parameters preventing the use of gradient descent optimization techniques. Instead, we focus on an approximation of the SURE based on finite differences as proposed in (Ramani et al., 2008). Under mild assumptions on the estimation mapping, we show that this approximation is a weakly differentiable function of the parameters and its weak gradient, coined the Stein Unbiased GrAdient estimator of the Risk (SUGAR), provides an asymptotically (with respect to the data dimension) unbiased estimate of the gradient of the risk. Moreover, in the particular case of soft-thresholding, the SUGAR is proved to be also a consistent estimator. The SUGAR can then be used as a basis to perform a quasi-Newton optimization. The computation of the SUGAR relies on the closed-form (weak) differentiation of the non-smooth function. We provide its expression for a large class of iterative proximal splitting methods and apply our strategy to regularizations involving non-smooth convex structured penalties. Illustrations on various image restoration and matrix completion problems are given. |
Image Denoising
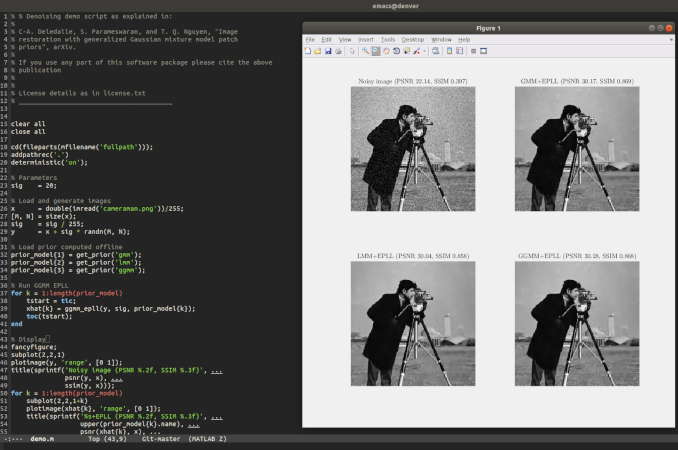
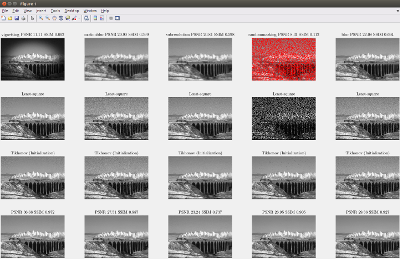
Matlab open-source software to perform image restoration with a GGMM prior. Patch priors have become an important component of image restoration. A powerful approach in this category of restoration algorithms is the popular Expected Patch Log-Likelihood (EPLL) algorithm. EPLL uses a Gaussian mixture model (GMM) prior learned on clean image patches as a way to regularize degraded patches. In this paper, we show that a generalized Gaussian mixture model (GGMM) captures the underlying distribution of patches better than a GMM. Even though GGMM is a powerful prior to combine with EPLL, the non-Gaussianity of its components presents major challenges to be applied to a computationally intensive process of image restoration. Specifically, each patch has to undergo a patch classification step and a shrinkage step. These two steps can be efficiently solved with a GMM prior but are computationally impractical when using a GGMM prior. In this paper, we provide approximations and computational recipes for fast evaluation of these two steps, so that EPLL can embed a GGMM prior on an image with more than tens of thousands of patches. Our main contribution is to analyze the accuracy of our approximations based on thorough theoretical analysis. Our evaluations indicate that the GGMM prior is consistently a better fit for modeling image patch distribution and performs better on average in image denoising task. |
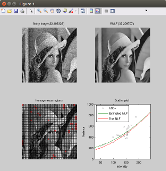
Matlab open-source software to perform (blind) denoising. It implements the followings
|
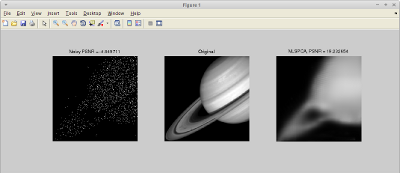
Matlab open-source software to perform non-local filtering in an extended PCA domain for Poisson noise. Photon-limited imaging arises when the number of photons collected by a sensor array is small relative to the number of detector elements. Photon limitations are an important concern for many applications such as spectral imaging, night vision, nuclear medicine, and astronomy. Typically a Poisson distribution is used to model these observations, and the inherent heteroscedasticity of the data combined with standard noise removal methods yields significant artifacts. A novel denoising algorithm is implemented for photon-limited images which combines elements of dictionary learning and sparse patch-based representations of images. The method employs both an adaptation of Principal Component Analysis (PCA) for Poisson noise and recently developed sparsity-regularized convex optimization algorithms for photon-limited images. A comprehensive empirical evaluation of the proposed method helps characterize the performance of this approach relative to other state-of-the-art denois ing methods. The results reveal that, despite its conceptual simplicity, Poisson PCA-based denoising appears to be highly competitive in very low light regimes. |
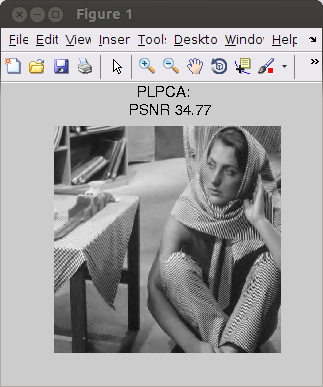
Matlab open-source software to perform non-local filtering in the PCA domain. In recent years, overcomplete dictionaries combined with sparse learning techniques became extremely popular in computer vision. While their usefulness is undeniable, the improvement they provide in specific tasks of computer vision is still poorly understood. The aim of the present work is to demonstrate that for the task of image denoising, nearly state-of-the-art results can be achieved using orthogonal dictionaries only, provided that they are learned directly from the noisy image. To this end, we introduce three patch- based denoising algorithms which perform hard thresholding on the coefficients of the patches in image-specific orthogonal dictionaries. The algorithms differ by the method- ology of learning the dictionary: local PCA, hierarchical PCA and global PCA. We carry out a comprehensive empirical evaluation of the performance of these algorithms in terms of accuracy and running times. The results reveal that, despite its simplicity, PCA-based denoising appears to be competitive with the state-of-the-art denoising algorithms, espe- cially for large images and moderate signal-to-noise ratios. |

Matlab open-source software to perform non-local filtering with shape adaptive patches. This implements an extension of the Non-Local Means (NL-Means) denoising algorithm. The idea is to replace the usual square patches used to compare pixel neighborhoods with various shapes that can take advantage of the local geometry of the image. We provide a fast algorithm to compute the NL-Means with arbitrary shapes thanks to the Fast Fourier Transform. We then consider local combinations of the estimators associated with various shapes by using Stein’s Unbiased Risk Estimate (SURE). Experimental results show that this algorithm improve the standard NL-Means performance and is close to state-of-the-art methods, both in terms of visual quality and numerical results. Moreover, common visual artifacts usually observed by denoising with NL-Means are reduced or suppressed thanks to our approach. |
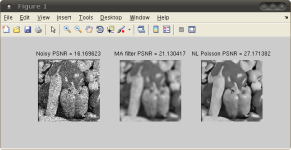
Matlab/Mex software to perform non-local filtering for Poisson noise with automatic selection of the denoising parameters. This work has been achieved by Charles Deledalle supervised by Florence Tupin and Loïc Denis. The aim was to adapt the Non-Local means (NL means) filter [1] to images sensed in low-light conditions. The Poisson NL means filter is based on the PPB filter [2] which ables to extend the NL means to deal with the Poisson distribution followed by the noise in such images. An efficient estimator has been designed, able to cope with the statistics and especially with the signal-dependent nature of such images. The Poisson NL means filter is an an extension of the non local (NL) [1] means for images damaged by Poisson noise. The proposed method is guided by the noisy image and a pre-filtered image and is adapted to the statistics of Poisson noise as recommended in [2]. The influence of both images can be tuned using two filtering parameters. These two parameters are automatically set to minimize an estimation of the mean square error (MSE). This selection uses an estimator of the MSE for NL means with Poisson noise and a Newton's method to find the optimal parameters in few iterations. |
SAR Speckle reduction
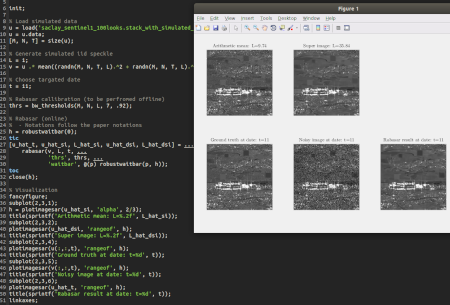
Matlab open-source software distributed under CeCILL license for speckle-reduction in multitemporal SAR image series. We propose a fast and efficient multi-temporal despeckling method. The key idea of the proposed approach is the use of the ratio image, provided by the ratio between an image and the temporal mean of the stack. This ratio image is easier to denoise than a single image thanks to its improved stationarity. Besides, temporally stable thin structures are well preserved thanks to the multi-temporal mean. The proposed approach can be divided into three steps: 1) estimation of a "super-image" by temporal averaging and possibly spatial denoising; 2) denoising of the ratio between the noisy image of interest and the "super-image"; 3) computation of the denoised image by re-multiplying the denoised ratio by the "super-image". Because of the improved spatial stationarity of the ratio images, denoising these ratio images with a speckle-reduction method is more effective than denoising images from the original multi-temporal stack. The amount of data that is jointly processed is also reduced compared to other methods through the use of the "super-image" that sums up the temporal stack. The comparison with several state-of-the-art reference methods shows better results numerically (peak signal-noise-ratio, structure similarity index) as well as visually on simulated and real SAR time series. The proposed ratio-based denoising framework successfully extends single-image SAR denoising methods to time series by exploiting the persistence of many geometrical structures. |
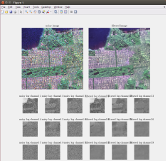
Python (or Matlab) open-source software distributed under CeCILL license to perform (Pol)(In)SAR filtering with embedded Gaussian denoiser. Speckle reduction is a longstanding topic in synthetic aperture radar (SAR) imaging. Since most current and planned SAR imaging satellites operate in polarimetric, interferometric or tomographic modes, SAR images are multi-channel and speckle reduction techniques must jointly process all channels to recover polarimetric and interferometric information. The distinctive nature of SAR signal (complex-valued, corrupted by multiplicative fluctuations) called for the development of specialized methods for speckle reduction. Image denoising is a very active topic in image processing with a wide variety of approaches and many denoising algorithms available, almost always designed for additive Gaussian noise suppression. This algorithm proposes a general scheme, called MuLoG (MUlti-channel LOgarithm with Gaussian denoising), to include such Gaussian denoisers within a multi-channel SAR speckle reduction technique. A new family of speckle reduction algorithms can thus be obtained, benefiting from the ongoing progress in Gaussian denoising, and offering several speckle reduction results often displaying method-specific artifacts that can be dismissed by comparison between results. |
Open-source software distributed under CeCILL license to perform adaptive non-local (Pol)(In)SAR filtering. Interface in command line, IDL, Matlab, Python and C dynamic library. Plug in for PolSARpro. Speckle noise is an inherent problem in coherent imaging systems like synthetic aperture radar. It creates strong intensity fluctuations and hampers the analysis of images and the estimation of local radiometric, polarimetric or interferometric properties. SAR processing chains thus often include a multi-looking (i.e., averaging) filter for speckle reduction, at the expense of a strong resolution loss. Preservation of point-like and fine structures and textures requires to locally adapt the estimation. Non-local means successfully adapt smoothing by deriving data-driven weights from the similarity between small image patches. The generalization of non-local approaches offers a flexible framework for resolution-preserving speckle reduction. NL-SAR is a general method that builds extended non-local neighborhoods for denoising amplitude, polarimetric and/or interferometric SAR images. These neighborhoods are defined on the basis of pixel similarity as evaluated by multi-channel comparison of patches. Several non-local estimations are performed and the best one is locally selected to form a single restored image with good preservation of radar structures and discontinuities. The proposed method is fully automatic and can handle single and multi-look images, with or without interferometric or polarimetric channels. Efficient speckle reduction with very good resolution preservation has been demonstrated both on numerical experiments using simulated data and airborne radar images. |

Matlab/Mex software of the PPB version for SAR interferometry. This work has been achieved by Charles Deledalle supervised by Florence Tupin and Loïc Denis. The aim was to adapt the Non-Local means (NL means) filter [7] to InSAR images. The NL-InSAR filter is based on the PPB filter [6] which is an extension of the NL means to non-gaussian noise and multivariate data. Then, an efficient estimator as been designed, able to cope with the statistical nature and the multi-dimensionnality of InSAR images. Interferometric synthetic aperture radar (InSAR) data provides reflectivity, interferometric phase and coherence images, which are paramount to scene interpretation or low-level processing tasks such as segmentation and 3D reconstruction. These images are estimated in practice from hermitian product on local windows. These windows lead to biases and resolution losses due to local heterogeneity caused by edges and textures. We propose a non-local approach for the joint estimation of the reflectivity, the interferometric phase and the coherence images from an interferometric pair of co-registered single-look complex (SLC) SAR images. Non-local techniques are known to efficiently reduce noise while preserving structures by performing a weighted averaging of similar pixels. Two pixels are considered similar if the surrounding image patches are "resembling". Patch- similarity is usually defined as the Euclidean distance between the vectors of graylevels. A statistically grounded patch-similarity criterion suitable to SLC images is derived. A weighted maximum likelihood estimation of the SAR interferogram is then computed with weights derived in a data-driven way. Weights are defined from intensity and interferometric phase, and are iteratively refined based both on the similarity between noisy patches and on the similarity of patches from the previous estimate.. |
Matlab/Mex software to perform iterative non-local filtering for reducing: additive white Gaussian noise or, multiplicative speckle noise, i.e Nakagami-Rayleigh distributions (NL-SAR). This work has been achieved by Charles Deledalle supervised by Florence Tupin and Loïc Denis. The aim was to adapt the Non-Local means (NL means) filter [2] to SAR images. Then, an efficient filter as been designed, able to cope with non Gaussian noise, multi-dimensionnal images and especially to the various existing SAR images. Results on the extended filter for amplitude SAR images are given on this page. The NL-InSAR filter is also an extension of the non-local means based on the PPB filter for interferometric SAR images, as well as the Poisson NL means filter for images sensed in low-light conditions. |
Edition

Open-source software distributed under CeCILL license for UNIX-like systems (such as Linux and MacOS-X). MooseTeX helps you generate high quality LaTeX documents of any kind such as articles, letters, reports, theses, presentations or posters. Based on the technology of Makefile(s), the purpose of MooseTeX is ``to determine automatically which pieces of a (large) LaTeX project need to be recompiled, and issue the commands to recompile them''. For doing so, MooseTeX also includes a suite of tools to recompile each of such pieces. Note that MooseTeX is non-intrusive. It does not change the way you use LaTeX and is, as a consequence, compatible with your older projects. You can also use MooseTeX within collaborative LaTeX projects without imposing the use of MooseTeX to other collaborators. |
Last modified: Mon Sep 18 07:40:41 Europe/Berlin 2023