Veux retourner!!
Résumé de ma thèse
Elle consiste en l'étude des idéaux fermés de deux algèbres ${\mathcal B}$ et ${\mathcal D}$ de fonctions continues sur le cercle unité $\Gamma$. Il s'agit d'algèbres à poids, un poids étant une application sous-multiplicative de ${\Bbb{Z}}$ dans $[1,+\infty]$. Ces algèbres sont de la forme

\begin{displaymath}\{f\in{\mathcal C}(\Gamma),\sum_{n\in\Bbb{Z}}\vert\hat{f}(n)\vert\omega_p(n)<+\infty\ (p\in\Bbb{N})\} \end{displaymath}

avec pour ${\mathcal B}$

\begin{displaymath}\omega_{{\mathcal B},p}(n)=\begin{cases} e^{p\sqrt{\vert n\vert}}\ (n<0)\\ (n+1)^p\ (n\ge0) \end{cases}\end{displaymath}

et pour ${\mathcal D}$

\begin{displaymath}\omega_{{\mathcal D},p}(n)=\begin{cases} e^{\frac{p\vert n\vert}{1+\log(\vert n\vert)}}\ (n<0)\\ (n+1)^p\ (n\ge0) \end{cases}\end{displaymath}

Ces algèbres sont incluses dans ${\mathcal C}^\infty(\Gamma)$ et leur duaux contiennent donc l'ensemble des distributions. On les décrit comme des ensembles d'hyperfonctions, une hyperfonction étant une fonction analytique sur $\Bbb{C}\setminus\Gamma$ tendant vers 0 en l'infini. Elles contiennent l'algèbre $A^\infty$ définie par

\begin{displaymath}A^\infty=\{f\in{\mathcal C}^\infty(\Gamma),\hat{f}(n)=0,(n<0)\} \end{displaymath}

dont les idéaux ont été complètement étudiés par B. A. Taylor et D. L. Williams. Comme pour cette algèbre, on a réussi dans certains cas pour ${\mathcal B}$et dans tous les cas pour ${\mathcal D}$ à décrire les idéaux à l'aide de conditions d'annulation des fonctions de l'idéal et de certaines de leurs dérivées en certains points du cercle, et à l'aide de fonctions intérieures singulières.
L'algèbre ${\mathcal B}$ est une algèbre régulière. Il est naturel de faire intervenir pour l'étude de ses idéaux I le sous-ensemble de $\Gamma$

\begin{displaymath}h(I)=\{z\in\Gamma,f(z)=0,(f\in I)\}, \end{displaymath}

et d'associer aux fermés E de $\Gamma$ les idéaux fermés

\begin{displaymath}I(E)=\{f\in{\mathcal B},f\mid_E\equiv0\} \end{displaymath}

et

\begin{displaymath}J(E)=\{f\in{\mathcal B}, f\text{ est limite dans }{\mathcal B}\text{ d'une suite de fonctions nulles au voisinage de }E\} \end{displaymath}

La régularité de ${\mathcal B}$ implique que h(I(E))=h(J(E))=Eet on a la double inclusion pour E=h(I)

\begin{displaymath}J(E)\subset I\subset I(E). \end{displaymath}

Les éléments de J(E) sont appelés fonctions de synthèse, et la géométrie de E peut entrainer que J(E)=I(E). Il est montré par E. H. Zerouali que c'est le cas pour les intervalles dès que le poids $\omega_p$ choisi conduit à une algèbre régulière. Des estimations établies par A. Atzmon permettent de montrer que certaines hyperfonctions S* associées aux fonctions intérieures singulières S sont élément des duaux ${\mathcal B}^*$ et ${\mathcal D}^*$ de ${\mathcal B}$ et ${\mathcal D}$. Ces hyperfonctions jouent un rôle déterminant dans la suite de ce travail. Le premier théorème de la thèse consiste à déterminer l'ensemble IS des solutions de l'équation

f.S*=0

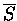où f.S* désigne le produit usuel d'une fonction f par l'hyperfonction S*. On obtient ainsi une famille d'idéaux fermés de ${\mathcal B}$ et on montre pour cette famille ainsi que pour J(E) des propriétés de stabilité par multiplication par les fonctions S et $\overline{S}$. Il parait raisonnable d'espérer que l'intersection des idéaux IS lorsque le support de la mesure définissant S est inclus dans le fermé E soit égale à J(E), mais cela n'a été montré que lorsque E est un ensemble dénombrable de points. Un des ingrédients pour cela est une propriété d'approximation par des fonctions extérieures pour les fonctions plates sur des ensembles de mesure nulle vérifiant une condition classique de Carleson, qui a aussi un interêt technique utilisé à plusieurs reprises dans la suite de ce travail. On décrit ensuite tous les idéaux I de ${\mathcal B}$ dont l'intersection avec l'algèbre $A^\infty$ est non réduite à $\{0\}$ en s'appuyant en particulier sur la structure des idéaux de $A^\infty$. Dans cette situation, on examine également l'équation

\begin{displaymath}f.\varphi=0 \text{ pour }f\in A^\infty\setminus\{0\}\text{ et }\varphi\in{\mathcal B}^* \end{displaymath}

et on établit en particulier que cette équation admet des solutions si et seulement si la restriction de $\varphi$ à D est dans la classe de Nevanlinna. Lorsque h(I) est un point $\lambda\in\Gamma$, les fonctions intérieures singulières S sont de la forme $S_{t,\lambda}=e^{t\frac{z+\lambda}{z-\lambda}}$. On considère alors pour un idéal fermé I tel que $h(I)=\lambda$ l'indice

\begin{displaymath}m_I(\lambda)=\sup\{t\ge0,\langle f,S_{t,\lambda}^*\rangle=0\} \end{displaymath}

et une propriété d'approximation découlant de la précédente ainsi qu'un résultat établit par A. Atzmon dans un cadre de théorie des opérateurs permettent de décrire ces idéaux lorsque $m_I(\lambda)=+\infty$, les cas où $m_I(\lambda)$est fini correspondant à la situation où $I\cap A^\infty\ne\{0\}$. L'utilisation d'une propriété géométrique élémentaire des fermés dénombrables du cercle - ils ont nécessairement un point isolé - permet alors de décrire tous les idéaux I de ${\mathcal B}$ tels que h(I) est dénombrable. Il serait intéressant de trouver des ensembles parfaits de mesure nulle dont on puisse décrire les idéaux fermés, mais cela n'a pas été fait pour ${\mathcal B}$ à ce stade.

En revanche, on a pu décrire tous les idéaux de l'algèbre ${\mathcal D}$. On montre en effet pour cette algèbre, qui est cette fois-ci quasianalytique, une description analogue à celle de ${\mathcal B}$ des idéaux fermés $I_{S,{\mathcal D}}=\{f\in{\mathcal D},f.S^*=0\}$ et des idéaux dont l'intersection avec $A^\infty$ est non réduite à $\{0\}$. En utilisant une propriété de factorisation montrée dans un cadre différent par A.A. Borichev, on montre que tous les idéaux non nuls de ${\mathcal D}$ ont une intersection avec $A^\infty$ qui n'est pas réduite à $\{0\}$.

Ces résultats ont une interprétation en termes de synthèse des hyperfonctions.

(retour...)