Nous allons utiliser l'outil pdetool de Matlab. A l'aide de cet outil, il est possible de réaliser facilement des maillages de formes élémentaires comme des disques, carrés. Si on veut bénéficier de fonctionnalités plus avancées, il est conseillé d'utiliser des mailleurs comme Gmsh.
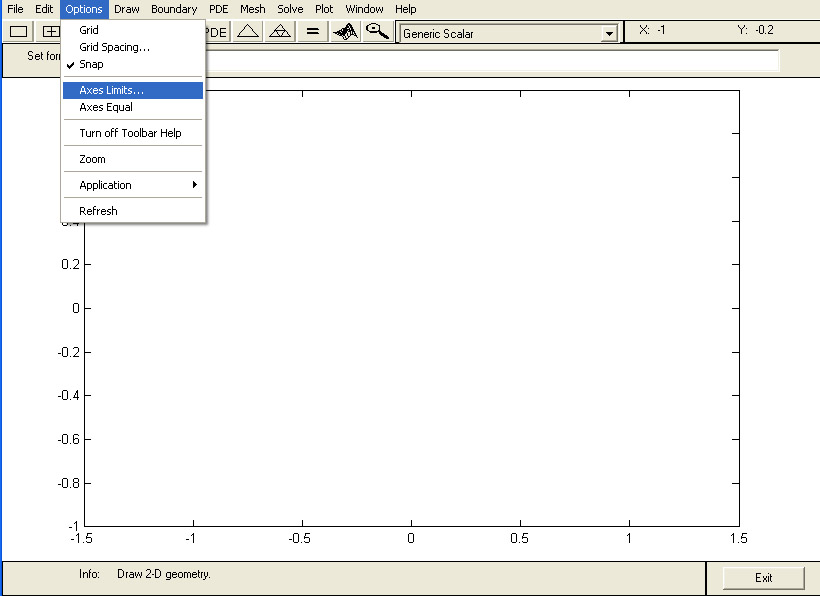
Lancez Matlab sur votre ordinateur, tapez pdetool. Vous avez à l'écran la figure 1. Nous allons détailler les étapes pour générer un maillage d'une couronne circulaire à l'aide de cet outil.

Figure 1 : Choix des axes
Sélectionnez le menu Options puis l'item Axes Limits.... Entrez les bornes du domaine de calcul, par exemple [-3,3] en x et [-2,2] en y. Sur ce même menu, vérifiez que l'item Snap soit activé. Cette fonctionnalité permet de forcer tout point à être sur un noeud de la grille.
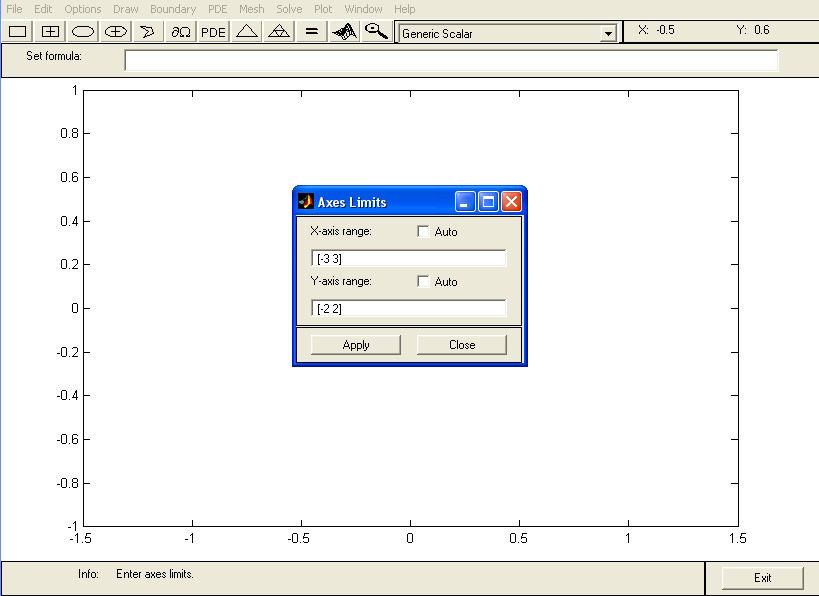
Figure 2 : Saisie des limites des axes
Cliquez sur l'icône de l'ellipse avec une croix en son centre, placez ensuite le curseur de la souris à l'endroit où vous voulez placer le centre de l'ellipse. Cliquez puis déplacez le curseur,en maintenant enfoncé le bouton gauche de la souris, afin de fixer le rayon de l'ellipse/cercle. Vous remarquez qu'en haut à droite, les coordonnées du curseur sont affichées. Créez ainsi un cercle centré à l'origine et de rayon 1.
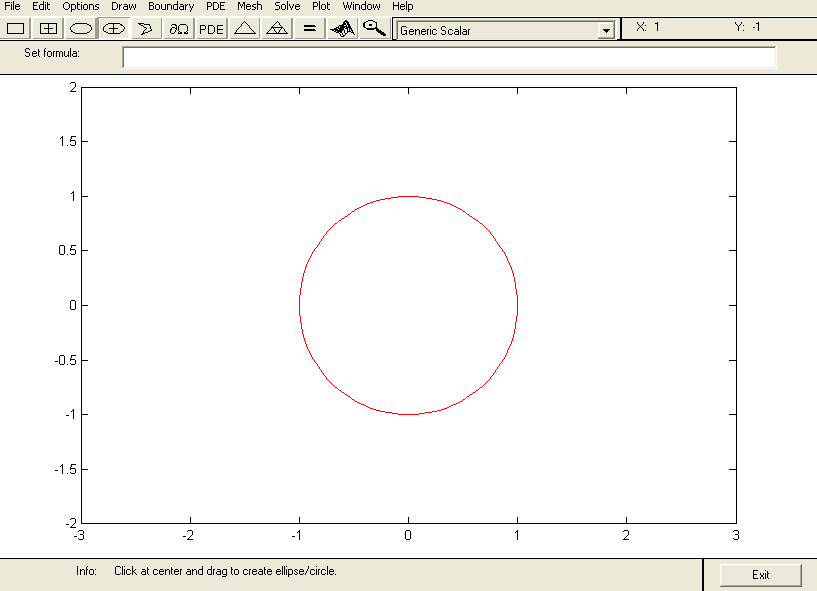
Figure 3 : Création d'un cercle
Une fois que vous avez relaché le bouton de la souris, Matlab donne un nom C1 à votre cercle. Répétez l'opération afin de dessiner un cercle C2 centré à l'origine et de rayon 2. Sur la ligne Set Formula , vous entrez la formule C2 - C1
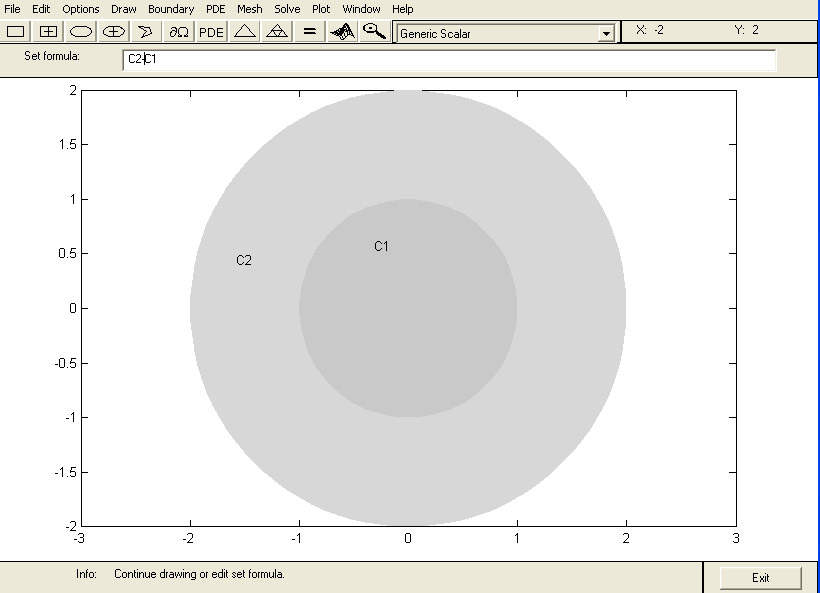
Figure 4 : Choix de la formule
L'étape de construction géométrique est terminée. Sélectionnez le menu Boundary puis l'item Boundary Mode.
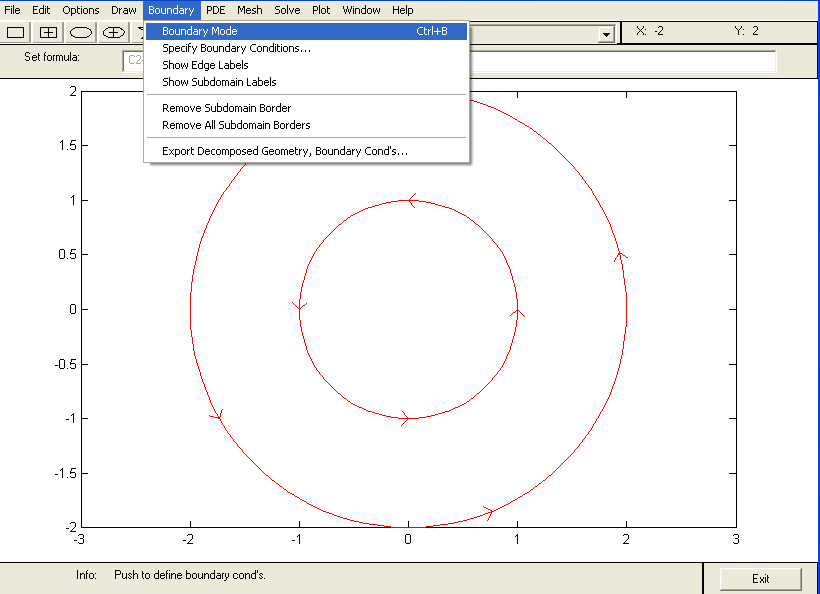
Figure 5 : Mode Boundary
Sur le menu Boundary , cliquez sur l'item Show Edge Labels , puis sur Show Subdomain Labels . Matlab vous affiche alors les numéros de référence attribués à chaque portion de la frontière du domaine de calcul. Ces numéros seront ultérieurement utilisés pour spécifier les conditions aux limites. Il affecte également le numéro 1 au domaine intérieur.
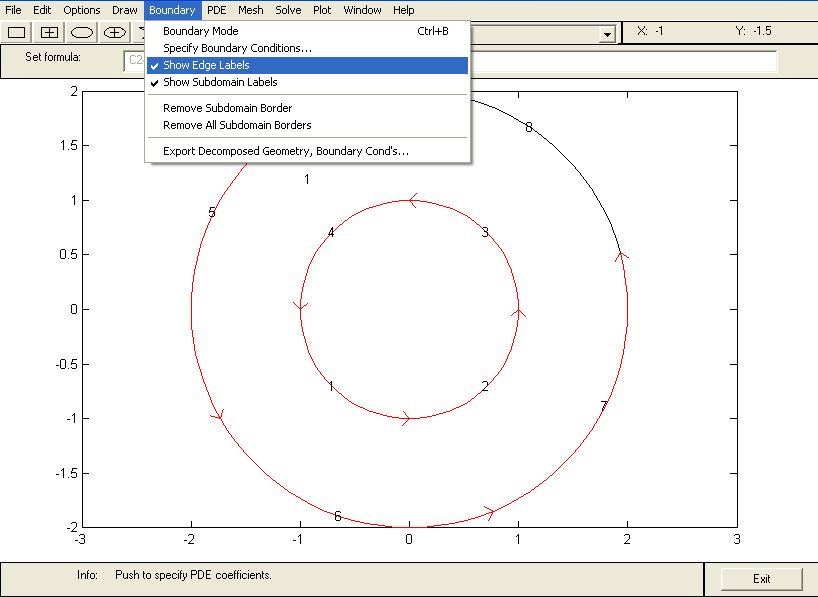
Figure 6 : Spécification des frontières du domaine
Dans le mode Boundary , vous ne pouvez plus changer la géométrie du domaine. Si vous désirez modifier la géométrie de l'objet, sélectionnez le menu Draw puis l'item Draw Mode. Vous serez alors dans le mode Draw . Cliquez sur l'icone du triangle, Matlab vous affiche le maillage obtenu.
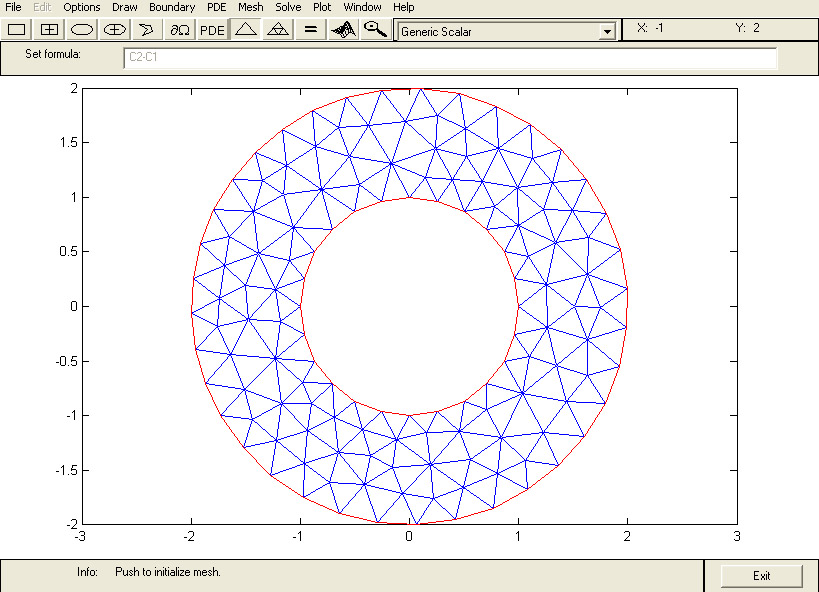
Figure 7 : Création du maillage
Sauvegardez votre travail en sélectionnnant le menu File puis l'item Save As... . Dans la boîte de dialogue qui apparaît, vous mettez un nom de fichier (couronne.m par exemple). Lors de votre prochaine session Matlab, vous pourrez retrouver votre travail en exécutant disque sur la ligne de commande Matlab. Maintenant que vous avez créé le maillage, il est nécessaire de l'exporter pour l'utiliser dans un code éléments finis. Sélectionnez le menu Mesh puis l'item Export Mesh... .
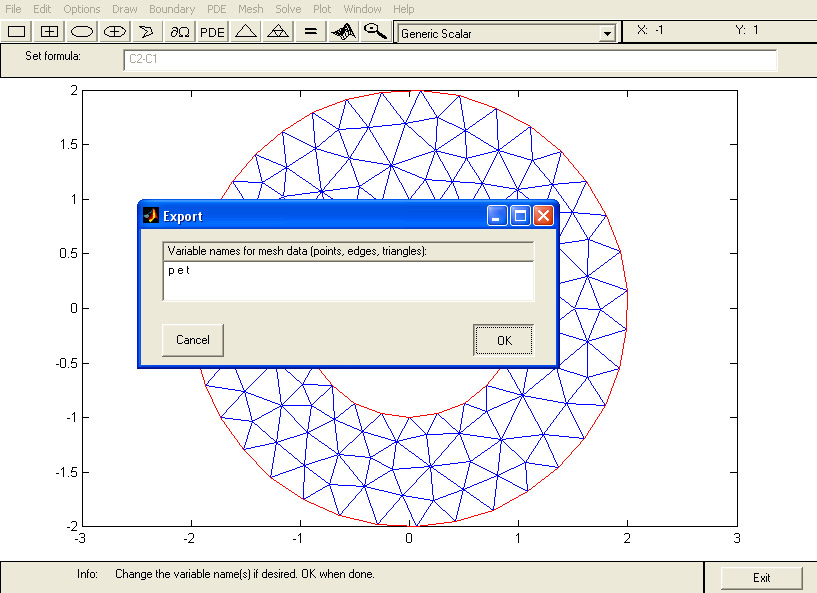
Figure 8 : Exportation du maillage
Cliquez sur ok. Dans votre espace de travail (workspace), vous avez trois nouvelles variables qui ont été créés : p, e et t. Si vous ne voyez pas d'espace de travail, vous pouvez afficher toutes les variables en tapant whos. La première variable créée p est la liste de tous les points du maillage (coordonnées). La variable e est la liste des arêtes placées sur la frontière du maillage. Le tableau e contient les numéros des deux extrémités de chaque arête ainsi que la référence de l'arête. La variable t contient les trois sommets de chaque triangle, ainsi qu'un numéro de référence.

Figure 9 : Sauvegarde du maillage
Sauvegardez le maillage dans un fichier, en tapant la commande sauver_maillage(p,e,t,'Disque.mesh'); . Cette commande stocke le maillage dans le fichier Disque.mesh . Vous pouvez recharger le maillage en tapant la commande [p,e,t] = charger_maillage('Disque.mesh'); . Si vous désirez uniquement visualiser le maillage stocké dans le fichier Disque.mesh , tapez afficher_maillage('Disque.mesh'); .
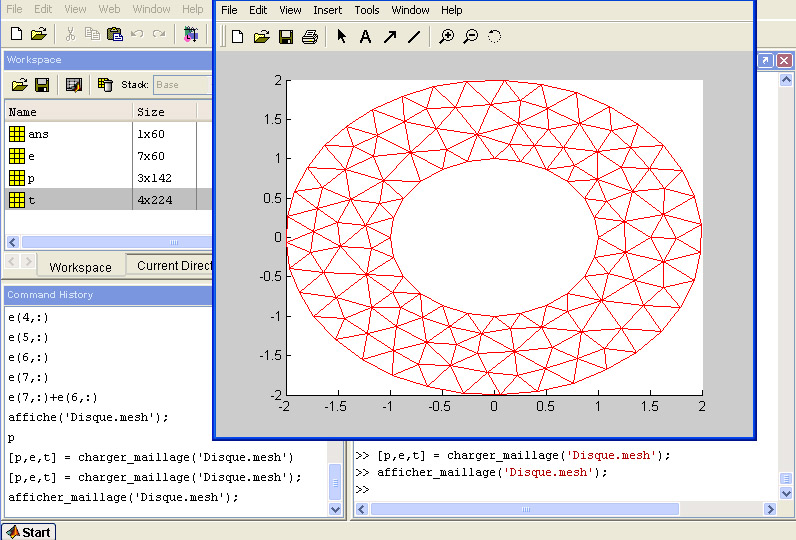
Figure 10 : Visualisation du maillage sous Matlab
Vous pouvez également visualiser le maillage en utilisant Medit Ce logiciel permet de visualiser des maillages 2-D,3-D ainsi que les solutions. Il suffit de taper sur un terminal medit Disque.mesh . Une fois le maillage à l'écran, tapez cbe . c comme color affiche le maillage en couleurs. b comme background bascule la couleur du fond d'écran (noir/blanc). e comme edit, bascule la couleur du domaine de maillage.
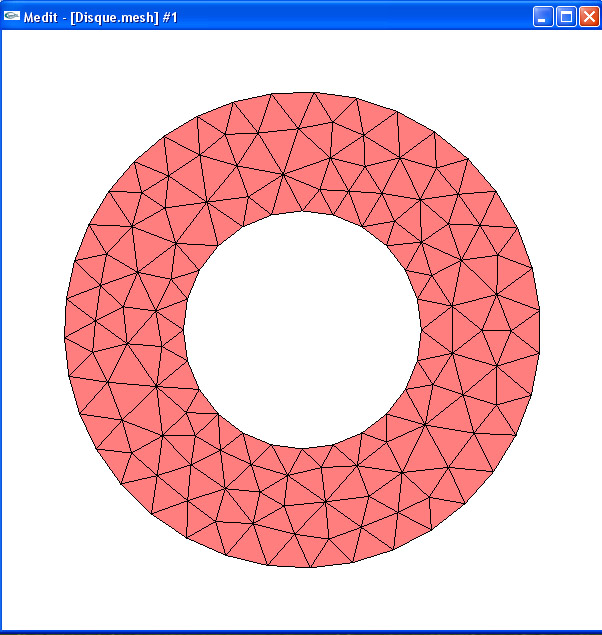
Figure 11 : Visualisation de maillage sous medit
Ceci fait l'objet du cours, on considère cette partie bien comprise. Numériquement le calcul se décompose en plusieurs étapes :
Dans cette partie, nous allons proposer deux possibilités de visualisation de la solution obtenue par le code éléments finis. Le premier choix est d'afficher directement la solution sur le maillage, en laissant le soin à Matlab d'effectuer l'interpolation, afin de donner un rendu lisse à l'écran. Le second choix est de calculer la solution sur une grille régulière, et d'afficher les valeurs sur cette grille.
On note x le vecteur solution. Le maillage est toujours stocké sur les trois variables p,e,t . Tapez alors sous matlab la commande trisurf(t(1:3,end)',p(1,:),p(2,:),real(x)); . Effectuez une rotation de la figure, jusqu'à obtenir le résultat de la figure 12.
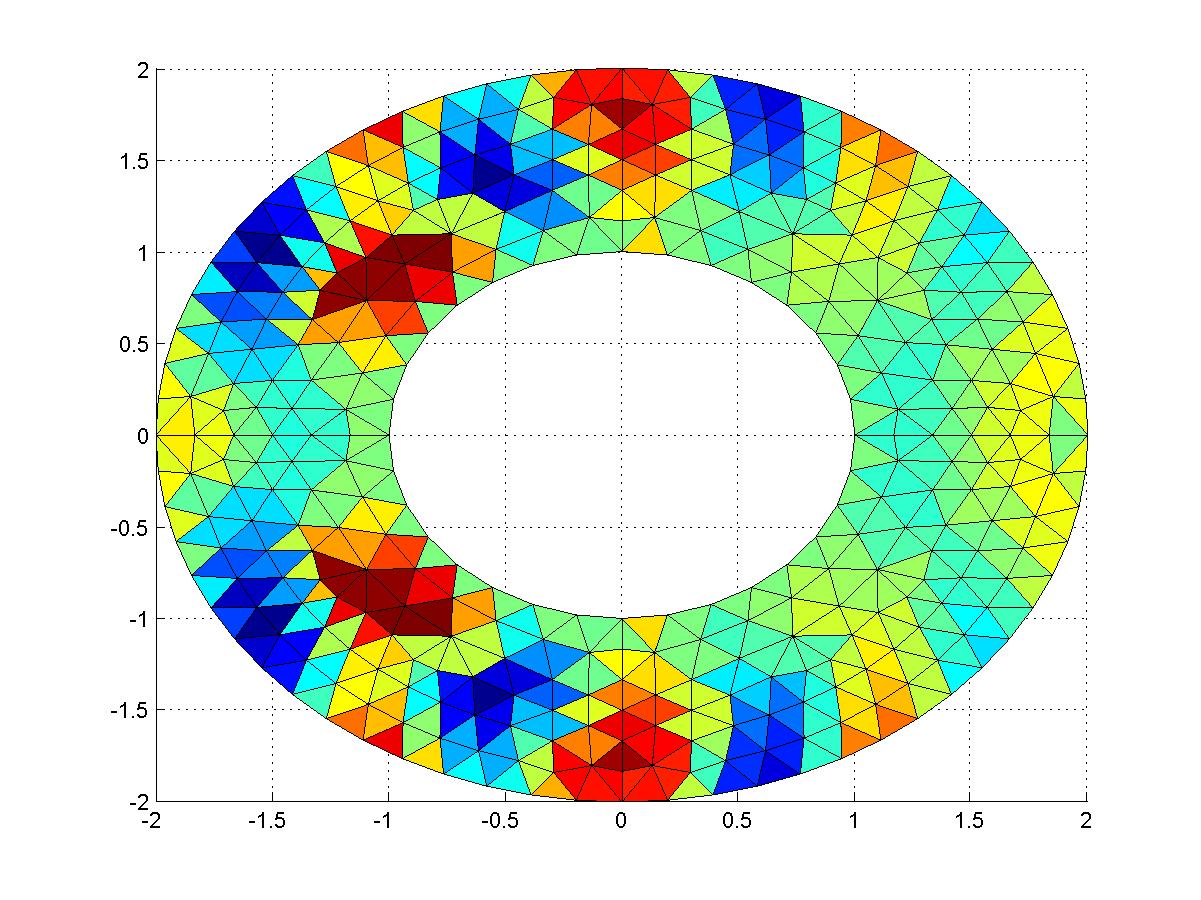
Figure 12 : Visualisation de la solution sous matlab
Une autre alternative plus intéressante est de calculer à l'aide du code éléments finis la solution sur une grille régulière. Une première étape du code consiste à localiser chaque point de la grille sur le maillage. Le code détermine, pour chaque point de la grille, le numé du triangle qui le contient et les coordonnées barycentriques de ce point dans le triangle.
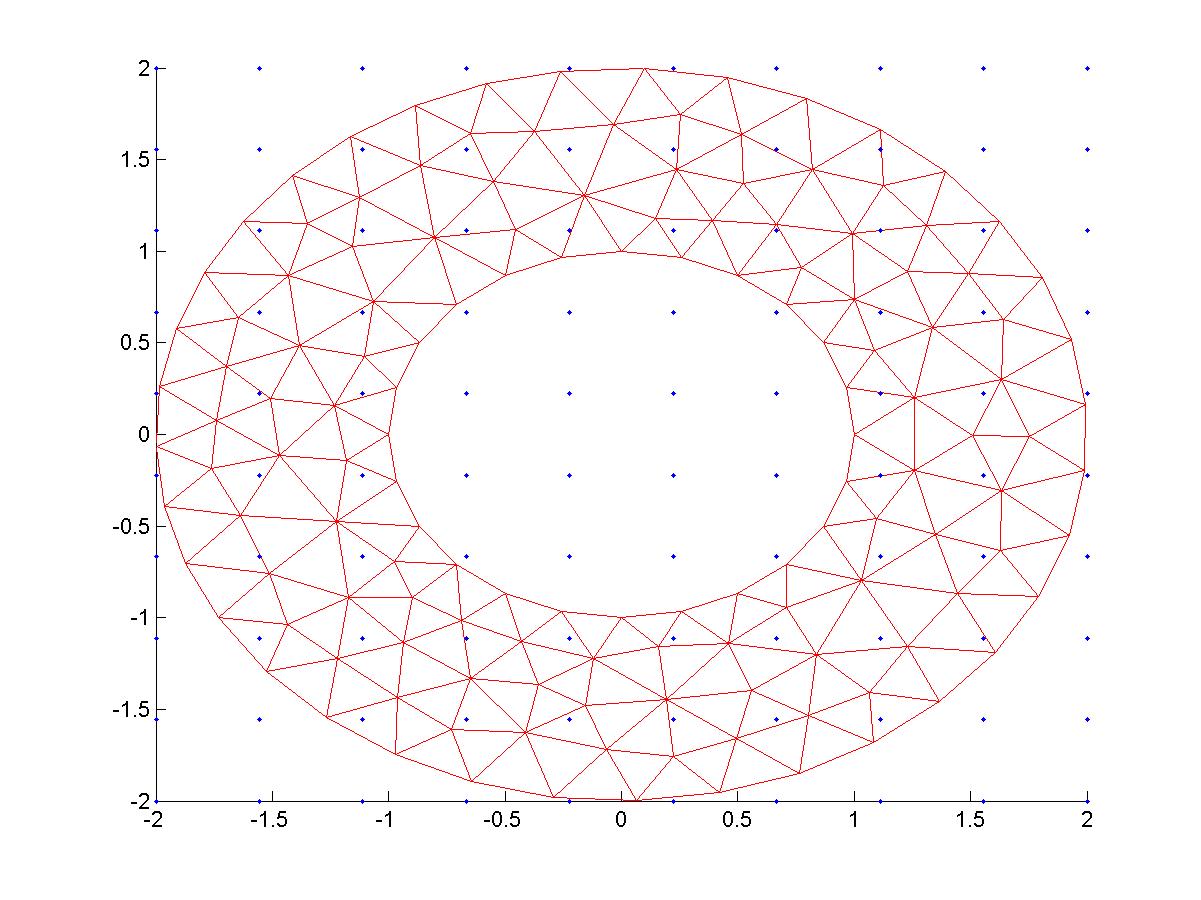
Figure 13 : Intersection maillage/grille régulière
Le code calcule ensuite les valeurs de la solution sur la grille régulière. On note X,Y,V respectivement, les abscisses des points de la grille, les ordonnées et les valeurs. Tous ces variables sont des matrices de taille m,n . Pour afficher la solution, tapez la commande plot2dinst(X,Y,real(V),-1,1); . Les deux derniers arguments déterminent l'échelle d'affichage de la solution.
L'avantage majeur de cette technique est que l'interpolation est faite grâce aux fonctions de base de l'élément fini utilisé et non par une fonction d'interpolation de Matlab. Un autre avantage est la comparaison possibles entre deux solutions obtenues sur des maillages différents.

Figure 14 : Visualisation de la solution sous Matlab, sur une grille régulière
On peut également visualiser la solution sous Medit . Lancez sous Matlab les commandes sauver_maillage(p,e,t,'Disque.mesh'); sauver_solution(real(x),'Disque.bb'); . Sur un terminal, exécutez la commande medit Disque.mesh , puis une fois le maillage affiché tapez cbem . m comme metric, permet de visualiser la solution contenue dans le fichier .bb . Vous devez obtenir la figure 15.
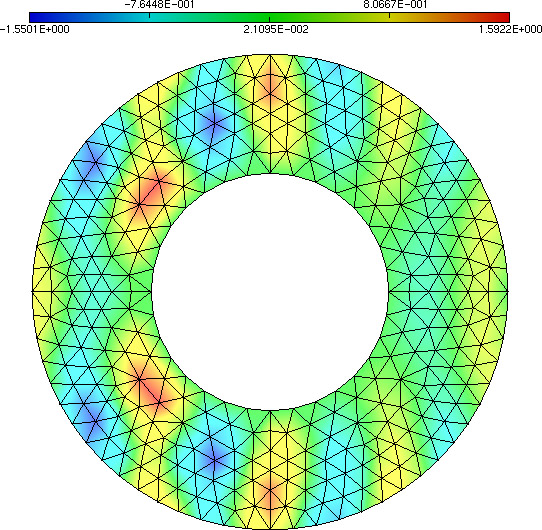
Figure 15 : Visualisation de la solution sous medit
Nous avons décrit toutes les étapes d'un calcul éléments finis, du prétraitement au post-traitement. Nous allons maintenant illustrer notre propos sur l'équation de Helmholtz, en utilisant des éléments finis triangulaires Pk isoparamétriques.
On considé dans un premier temps la diffraction d'une onde plane par un disque. Les conditions aux limites sont indiquées sur la figure 16
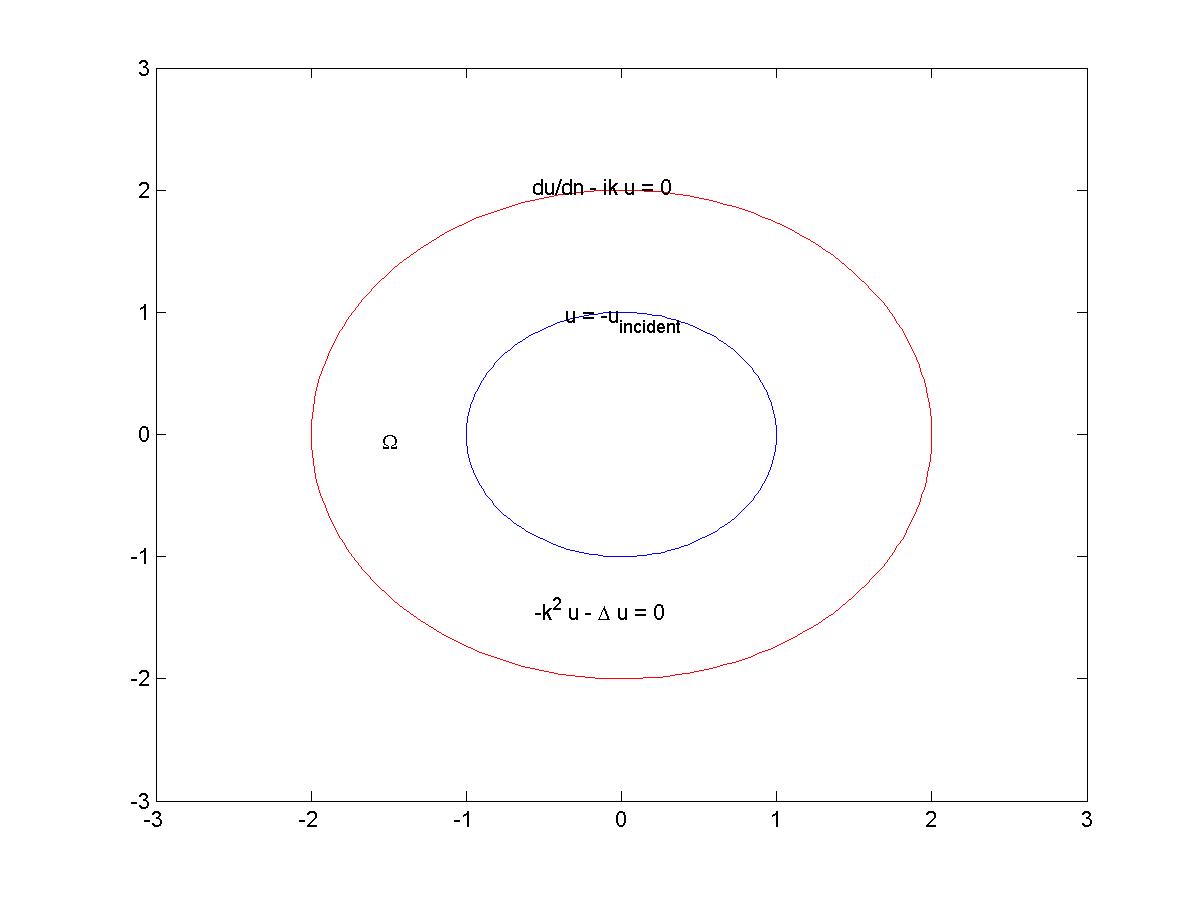
Figure 16 : Problème modèle étudié
On prend un maillage relativement grossier (voir figure 17).
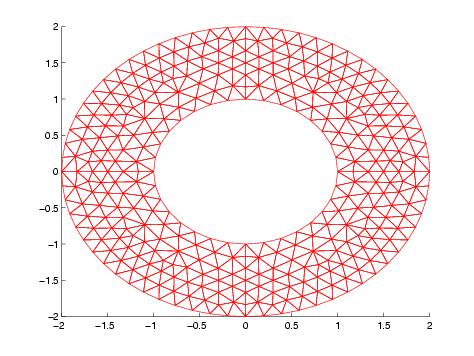
Figure 17 : Maillage utilisé
On calcule la solution sur ce maillage avec des éléments finis P1 et P2.
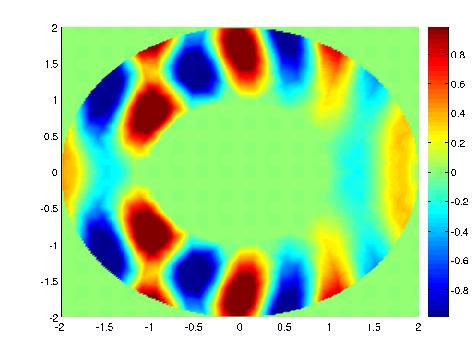
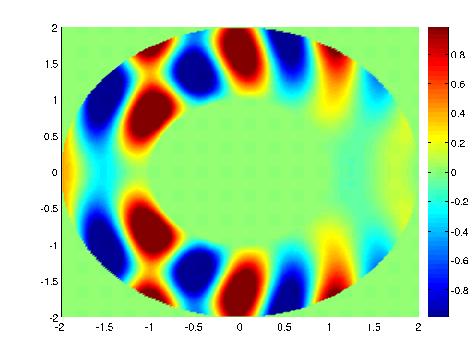
Figure 18 : Partie réelle du champ total pour P1 et P2
On calcule l'erreur entre la solution numérique et la solution analytique, lorsque le pas de maillage tend vers zéro. On utilise des éléments classiques, on observe une ordre 2 de convergence pour P1, P2 et P3. La mauvaise convergence de P2 et P3 est due à une mauvaise approximation de la géométrie circulaire.
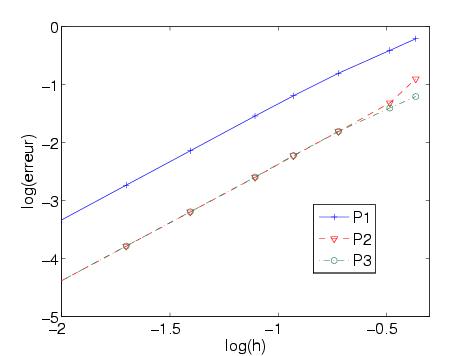
Figure 19 : Evolution de l'erreur en fontion du pas de maillage. Eléments finis "droits".
On effectue la même étude, cette fois-ci avec des éléments finis isoparamétriques. On observe un ordre de convergence 2,3 et 4 pour respectivement P1,P2 et P3.
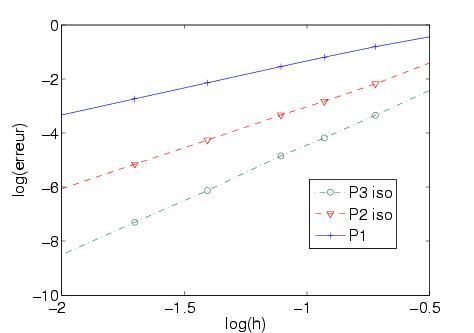
Figure 20 : Evolution de l'erreur en fontion du pas de maillage. Eléments finis "courbes".
La gémétrie circulaire ne présente pas de coin, la solution est infiniment régulière. Prenons, maintenant l'exemple d'un objet avec coins, comme sur la figure 21
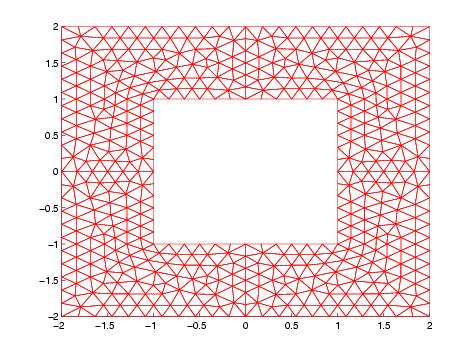
Figure 21 : Diffraction d'un carré
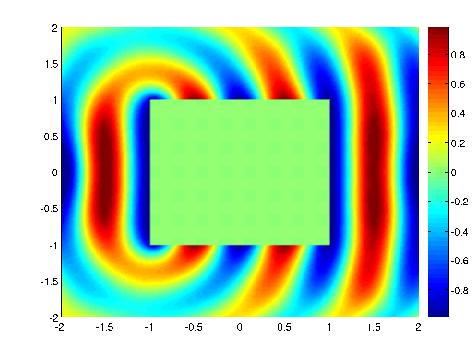
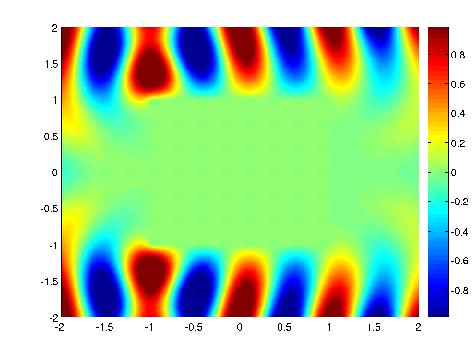
Figure 22 : Partie réelle du champ diffracté et du champ total;
Les éléments finis d'ordre élevé donnent de moins bons résultats que dans le cas du cercle, comme le montre la figure 23.
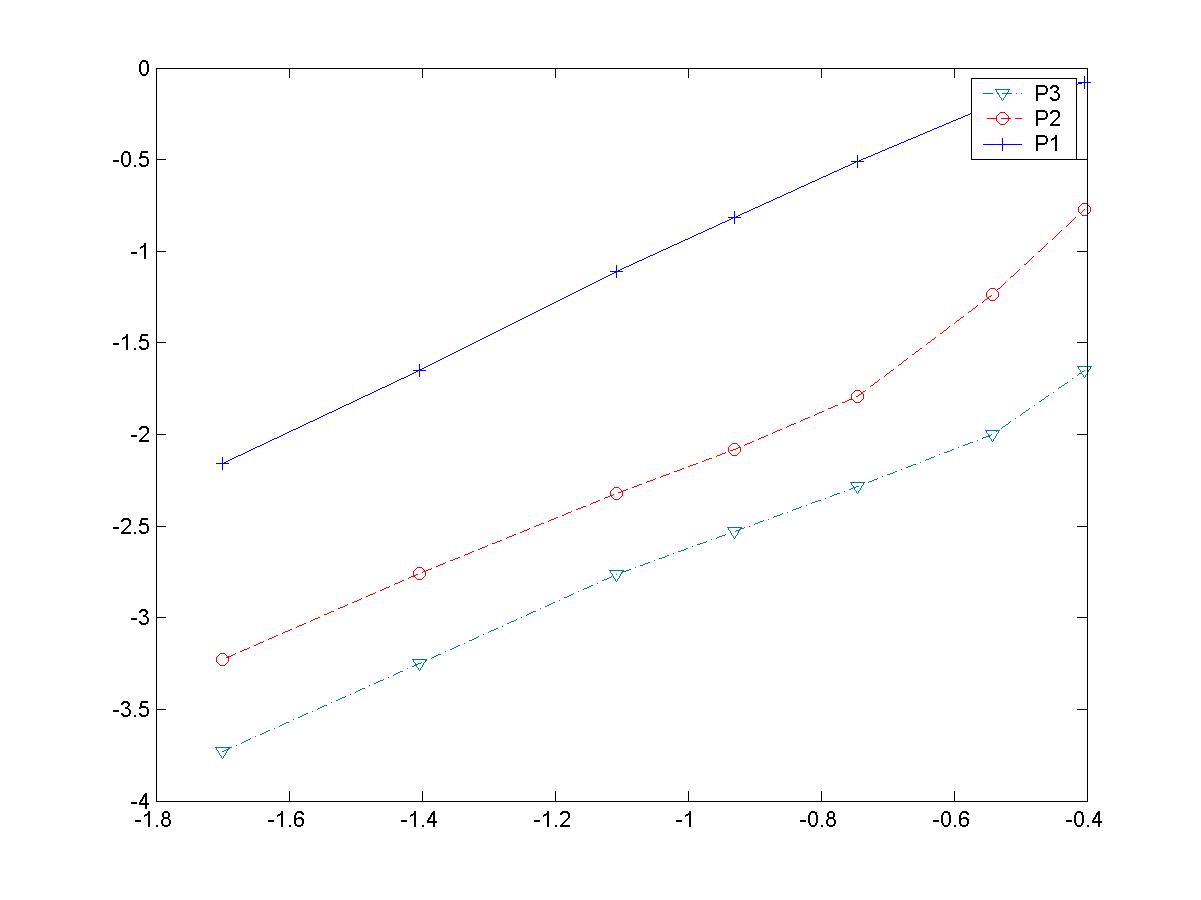
Figure 23 : Evolution de l'erreur en fontion du pas de maillage.
On conclura sur le coût de calcul en fonction du pas de maillage
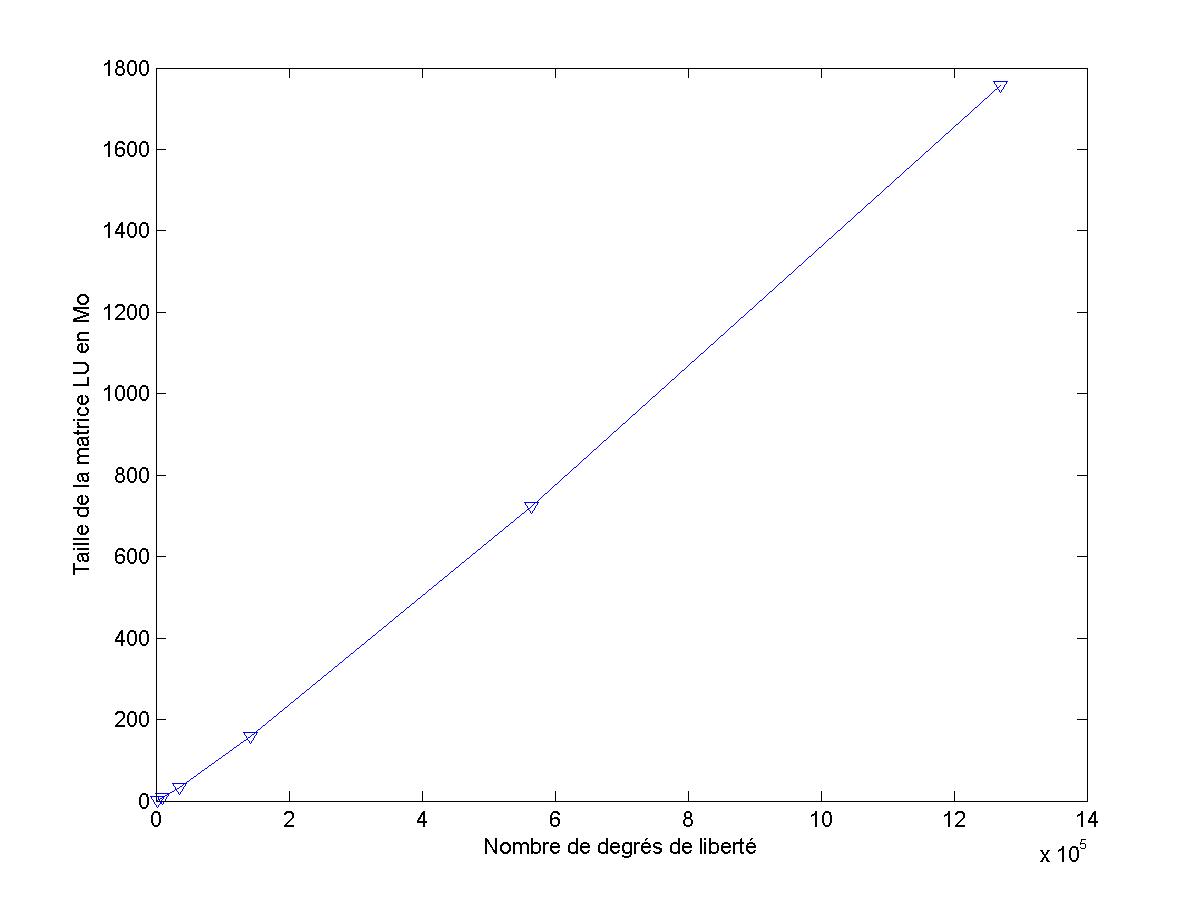
Figure 24 : Stockage en fonction du nombre de degrés de liberté