Equations différentielles, TP Programmation

On rappelle qu'on s'intéresse à la résolution de l'ODE suivante:

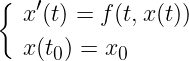
f est une fonction donnée, t₀ est le temps initial et x₀ la condition initiale. On veut connaitre la solution au temps final t_f, on calcule la solution aux temps

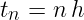
h est le pas de temps.

Implémentation de schémas explicites

Schéma d'Euler explicite

Dans un premier temps, on considère le schéma d'Euler explicite, qui sécrit ainsi:

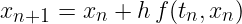
Créer un fichier ODE.py (avec emacs par exemple) dans le répertoire de votre convenance. Dans ce fichier on implémentera la fonction ode_solve en commençant ainsi:

# inclut les fonctions necessaires au TP:
from pylab import *

def ode_solve(f, x0, t0, tf, h):
    # nombre d'iterations en temps
    nb_iter = int(ceil((tf-t0) / h))
    # on recalcule le pas de temps pour tomber pile sur tf
    h = (tf - t0) / nb_iter

    # on initialise les vecteurs tn et xn
    tn = zeros(nb_iter+1)
    xn = zeros(nb_iter+1)

    # ecrire ici votre code qui calcule la suite des xn avec le schema d'Euler
   

    # a la fin de la fonction il faut retourner t_n et x_n
    return tn, xn

Cette fonction doit calculer les itérés x_n avec la méthode d'Euler explicite et les stocker dans le tableau xn (ainsi que les temps tn). On pourra ensuite tester la fonction ode_solve pour la fonction f suivante:

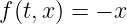
Pour tester la fonction, on lancera ipython en mode console avec la commande :

ipython --pylab

Une fois la console prête, on inclura les fonctions définies dans le fichier ODE.py avec la commande:

from ODE import *

On peut alors tester ode_solve comme suit:

f = lambda t, x : -x
tn, xn = ode_solve(f, x0=1.0, t0=0.0, tf=1.0, h=0.1)
plot(tn, xn)

On rappelle qu'une fois qu'un fichier est importé (ici ODE.py), on ne peut plus le recharger. Il faut au préalable sortir de la console (Ctrl+D) et relancer la console. On peut rappeler une ancienne commande avec les flèches (haut et bas). On affichera sur le même graphe la solution exacte:

plot(tn, exp(-tn))

Elle devrait s'afficher en vert (bleu pour la solution approchée). On peut ensuite visualiser les problèmes d'instabilité du schéma d'Euler en prenant :

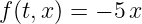
Calculer la solution numérique pour les paramètres suivants :

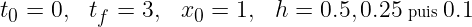
Visualiser la solution pour ces trois pas de temps ainsi que la solution exacte. Vous devez visualiser les différents comportements vus en TD. Vous pouvez afficher l'erreur relative en tapant dans la console ipython :

norm(xn - exp(-5*tn) ) / norm(xn)

Vérifier qu'en divisant le pas de temps par deux, l'erreur relative est bien divisé par deux (le schéma d'Euler explicite est un schéma d'ordre un. Écrire dans ODE.py une fonction ode_order qui calcule l'erreur en fonction du pas de temps (pour f = -x):

# calcul de l'erreur pour h0, h0 /ratio, h0/(ratio*ratio), ...
def ode_order(tf, h0, ratio, level):
  # on prend f(x) = -x
  f = lambda t, x : -x
  h = zeros(level)
  err = zeros(level)
  
  # on calcule h et err

  # on les retourne a la fin
  return h, err

On pourra tester la fonction ode_order dans la console ipython en tapant

h, err = ode_order(1.0, 0.5, 1.5, 10);
loglog(h, err)

La commande loglog permet d'afficher l'erreur directement en échelle logarithmique. Vous devez obtenir une droite de pente 1 (puisque la méthode est d'ordre 1.

Implémentation de schémas de Runge-Kutta explicites

Afin d'implémenter différents schémas numériques, on introduira une fonction euler qui calcule l'itéré x_n+1 en fonction de x_n comme suit:

# implementation d'un pas de la methode d'Euler
def euler(f, tn, xn, h):
    x_next = xn + h*f(tn, xn)
    return x_next

Modifier ode_solve pour prendre en argument le schéma à utiliser:

def ode_solve(f, x0, t0, tf, h, schema):
   # il faut appeler schema a chaque iteration

qu'on testera ainsi:

tn, xn = ode_solve(f, x0=1.0, t0=0.0, tf=1.0, h=0.1, schema=euler)

Modifier aussi la fonction ode_order pour prendre en argument le schéma utilisé. Implémenter ensuite le schéma RK2 suivant (méthode du point-milieu):

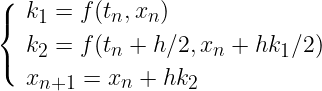
Vérifier que cette méthode est bien d'ordre 2. Implémenter ensuite le schéma RK4:

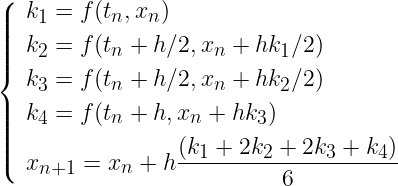
Vérifier que cette méthode est bien d'ordre 4. On s'intéresse maintenant au cas d'une EDO vectorielle :

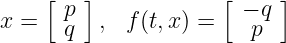
Modifier ode_solve pour qu'il accepte des scalaires ou des vecteurs:

m = 1
if (type(x0) == ndarray):
   m = len(x0)
    
xn = zeros([nb_iter+1, m])
xn[0,:] = x0

Tester ensuite l'implémentation avec ce choix de f:

f = lambda t, x : array([-x[1], x[0]])
tn, xn = ode_solve(f, x0=array([1.0, 0.0]), t0=0.0, tf=5.0, h=0.1, schema=RK4)
plot(tn, xn[:, 0])
plot(tn, xn[:, 1])
plot(tn, cos(tn))
plot(tn, sin(tn))

On pourra afficher la quantité suivante :

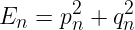
en fonction du temps. Afficher cette quantité pour le schéma d'Euler pour les paramètres suivants :

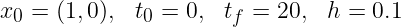
Pour la solution exacte, cette quantité doit se conserver. Afficher cette quantité pour le schéma de RK2 pour les paramètres suivants :

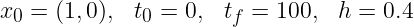
Afficher cette quantité pour le schéma de RK4 pour les paramètres suivants :

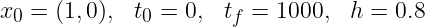
et RK4 de nouveau avec ces paramètres:

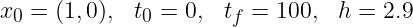
Cet exemple illustre les instabilités qu'on rencontre avec les schémas explicites.

Solutions des EDOs du polycopié

On préferera ici l'utilisation du schéma RK4 qui est plus précis que les autres schémas testés. On pourra calculer la solution numérique de l'EDO de l'exo 2:

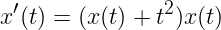
pour plusieurs conditions initiales x0=-1, -0.5, 0.5. Pour la dernière condition initiale, il faut prendre un temps final tf < 1.5 pour éviter un overflow. On pourra calculer la solution de l'EDO de l'exo 10

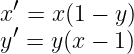
qu'on testera pour plusieurs conditions initales différentes du point stationnaire (1, 1). On pourra afficher la trajectoire:

plot(xn[:, 0], xn[:, 1])

pour ces différentes conditions initiales.

Calcul numérique des domaines de stabilité

Pour calculer le domaine de stabilité ` un pas de temps, il suffit d'évaluer la fonction de stabilité noté R tel que

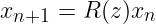
lorsque 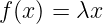avec 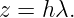Pour RK2, on avait obtenu

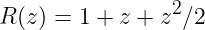
Pour calculer le domaine de stabilité de RK2, il suffit de taper sur ipython:

x = linspace(-2.8, 0.2, 301);
y = linspace(-3.0, 3.0, 301);
xi, yi = meshgrid(x, y);
z = xi+1j*yi;
R = abs(1+z+z**2/2)
stab = (R>1.0+1e-12).astype(float)
imshow(stab, cmap=cm.hot, extent=(x[0], x[-1], y[0], y[-1]))
    

La fonction meshgrid permet ici juste de tensoriser les vecteurs x et y pour avoir une matrice de points xi, yi sur le rectangle qu'on a choisi. Le tableau est rempli de 0 (point stable) et de 1 (point instable), en conséquence le domaine de stabilité s'affiche en noir. On peut aussi afficher le contour de ce domaine en appelant la fonction contour:

contour(stab, extent=(x[0], x[-1], y[0], y[-1]));
axis('equal')

On peut aussi afficher le domaine de stabilité le long de l'axe imaginaire en tapant

plot(stab[:, 280])

Pour RK2, cet intervalle est réduit à un singleton (quand z=0). Afficher le domaine de stabilité pour RK3 et RK4 qui possèdent les fonctions de stabilité suivantes

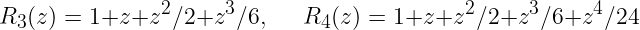
On pourra aussi afficher le domaine de stabilité sur l'axe imaginaire. Pour les schéma multi-pas, le facteur d'amplification R(z) est plus difficile à calculer car il faut calculer les racines de l'équation caractéristique. Par exemple, le schéma d'Adams-Bashforth d'ordre 2 (noté AB2) s'écrit :

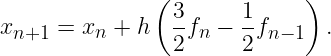
Lorsque 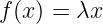, on obtient que x_n satisfait la relation de récurrence:

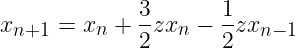
L'équation caractéristique associée à cette suite vaut

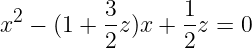
R(z) est alors le maximum (en module) des deux racines de cette équation. Pour l'évaluer, on peut faire une boucle sur tous les points :

R = zeros([len(x), len(y)]);
for i in range(len(x)):
    for j in range(len(y)):
       P = poly1d([1.0, -1.0-1.5*z[i, j], +0.5*z[i, j]])
       R[i, j] = abs(P.r).max()

On affiche le domaine de stabilité comme d'habitude:

stab = (R>1.0+1e-12).astype(float)
imshow(stab, cmap=cm.hot, extent=(x[0], x[-1], y[0], y[-1]))

Si on veut comparer AB2 avec RK2, il faut prendre en compte que RK2 demande deux fois plus d'évaluations qu'AB2. Il faut alors par exemple calculer le domaine de stabilité d'AB2 sur le rectangle [-1.4, 0.1] x [-1.5, -1.5] et le domaine de RK2 sur le rectangle [-2.8, 0.2] x [-3, 3]. Afficher le domaine de stabilité d'AB3 défini par la suite:

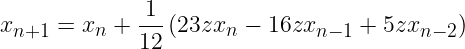
On pourra comparer avec RK3 qui demande trois fois plus d'évaluations qu'AB3.

Implémentation du schéma d'Euler implicite

On s'intéresse au schéma d'Euler implicite :

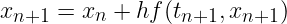
Cas linéaire

On s'intéresse dans un premier temps au cas d'une fonction f linéaire. On note Df la matrice associée à f. A chaque itération, on doit résoudre le système linéaire

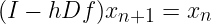
Modifier la fonction ode_solve afin de prendre non-seulement la fonction f en argument, mais aussi la jacobienne Df. Modifier également les schémas explicites pour mettre Df en argument du schéma (cet argument ne sera utilisé que pour les schémas implicites). Implémenter le schéma d'Euler implicite en utilisant la fonction solve de pylab:

# calcul de x = A^{-1} b
x = solve(A, b)

On testera ce schéma sur la fonction (et jacobienne) suivante

f = lambda t, x : array([-x[1], x[0]])
df = lambda t, x : array([[0.0, -1.0], [1.0, 0.0]])

On affichera la quantité :

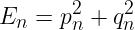
avec Euler implicite pour plusieurs pas de temps (par exemple h=0.1, 0.2 et 0.5), on vérifiera que l'algo reste toujours stable contrairement aux schémas explicites.

Cas non-linéaire

Dans le cas où f est non-linéaire, on note

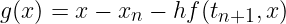
A chaque pas de temps, il faut résoudre:

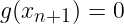
On résout ce système avec la méthode de Newton:

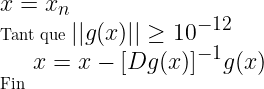
où Dg est la jacobienne de g. Cette jacobienne s'exprime avec la jacobienne de f (notée Df):

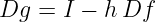
Implémenter le schéma d'Euler implicite dans le cas non-linéaire. On choisira comme application l'EDO suivante:

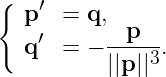
p et q sont ici deux vecteurs de taille 2. On prend la norme euclidienne

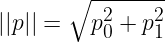
p₀ et p₁ les deux composantes de p. La jacobienne de la fonction f associée à l'EDO vaut:

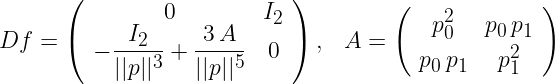
I₂ représente la matrice identité de taille 2. Tester avec la condition initiale (1, 0, 0, 1) et un temps final de 10 (pour h =0.01 avec Euler implicite). On pourra comparer les différents schémas codés sur cette dernière EDO. On pourra afficher la norme de p (qui doit se conserver pour ce jeu de conditions initiales).