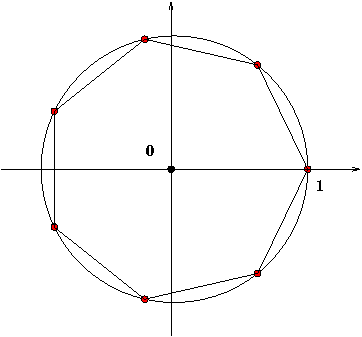
Les 7 solutions de l'équation x7 = 1
Note: si vous utilisez Netscape et qu'il écrit des symboles bizarres en lieu et place de symboles mathématiques, voici comment arranger ça.
"Il n'est pas possible de décomposer un cube en somme de deux cubes, une puissance quatrième en somme de deux puissances quatrièmes et généralement aucune puissance d'exposant supérieur à 2 en deux puissances de même exposant".
Cette courte annotation d'un magistrat français, Pierre Fermat, écrite en marge d'un livre de mathématiques dans la première moitié du 17e siècle, est devenue peu à peu un des théorèmes les plus célèbres des mathématiques : une preuve n'en fut en effet achevée qu'en... 1995, par Andrew Wiles de l'université de Princeton.
Pierre Fermat (1601?-1665), conseiller au parlement de Toulouse, fut l'un des mathématiciens les plus importants du 17e siècle ; en même temps que René Descartes, il eut l'idée de la géométrie analytique, c'est-à-dire de la transcription algébrique des problèmes de géométrie, pour étudier les tangentes à une courbe par exemple. En collaboration avec Blaise Pascal, il inventa le calcul des probabilités. Et avec Marin Mersenne ou Bernard Frenicle de Bessy qui fit partie de la première Académie des sciences, il s'intéressa aux problèmes sur les nombres entiers. A cette époque, les deux grandes branches des mathématiques théoriques étaient la géométrie et l'arithmétique, qui géraient l'une les grandeurs continues, l'autre les grandeurs discrètes. En particulier, même si l'algèbre était connue - elle fut développée dans les pays islamiques dès la période médiévale -, elle ne paraissait pas nécessairement bien adaptée pour traiter des problèmes sur les entiers : la solution d'une équation à coefficients entiers n'est pas nécessairement entière. Les problèmes sur les nombres étaient en général énoncés, soit sur des exemples numériques, soit avec des mots de la langue ordinaire - la citation du début de cet article en est un bon exemple. Fermat mit au point plusieurs méthodes pour mettre l'algèbre au service de l'arithmétique théorique, en particulier la méthode de descente infinie.
L'histoire du théorème de Fermat est exemplaire d'un phénomène fréquent en mathématiques, le changement de cadres. Pendant les trois siècles et demi qui séparent l'énoncé de sa preuve, ce théorème a été en effet retranscrit, réinterprété, partiellement prouvé, en utilisant des méthodes et des langages issus de branches variées des mathématiques. A commencer par l'utilisation de simples notations algébriques, absentes de l'original. Nous avons maintenant beaucoup plus l'habitude du symbolisme algébrique et nous allons donc réécrire le problème de Fermat sous sa forme plus connue, depuis la fin du 17e siècle. "Soit n un entier au moins égal à trois. Il n'existe pas de nombres entiers non tous nuls (ni même d'ailleurs de rationnels) vérifiant l'équation
On remarque que pour n=2, il y a au contraire une infinité de solutions, par exemple 25 = 16 + 9 ou 169 = 25 + 144, ou encore 29x29 = 21x21 + 20x20.
La méthode de descente infinie permit à Fermat de prouver le théorème pour n=4 et peut-être au moins dans ses grandes lignes pour n=3 ; on doute d'ailleurs qu'il ait possédé une preuve complète du théorème. Celui-ci fut établi pour les exposants 5 et 7 au début du 19e siècle, mais les détails se compliquaient très vite.
Un grand pas fut franchi lors d'un de ces changements de cadres dont nous avons parlé plus haut, grâce au travail de Ernst Eduard Kummer, un universitaire allemand. Celui-ci s'intéressait en particulier à ce qu'on appelle les lois de réciprocité entre nombres premiers. Par exemple, si q est un nombre premier, q est un carré à un multiple de 5 près si et seulement si 5 est un carré à un multiple de q près. Ainsi q = 269 = 132 + 5 x 20 est un carré à un multiple de 5 près. Donc si on examine la suite 5 + 269, 5 + 2 x 269, 5 + 3 x 269 ... on tombera fatalement sur un carré. Il y en aura même une infinité - le premier est 15876 = 1262 = 5 + 59 x 269.
Au début du 19e siècle, un autre mathématicien, Carl-Friedrich Gauss, avait utilisé, pour simplifier les preuves très difficiles de cette loi, certains nombres algébriques sur lesquels il était parvenu à faire de l'arithmétique comme sur les entiers usuels, par exemple en les factorisant en nombres premiers ou en effectuant des divisions euclidiennes. Pour généraliser ces travaux, Kummer essaya de faire de l'arithmétique sur les nombres de la forme x + z y, où x et y sont des entiers et z un nombre complexe tel que zn = 1 (on les appelle cyclotomiques). Les nombres utilisés par Gauss en sont un cas particulier. Kummer découvrit des difficultés majeures pour généraliser l'arithmétique usuelle : il n'existe pas par exemple de décomposition unique en facteurs premiers pour ces nombres. Il parvint cependant, en inventant une nouvelle sorte de nombres, à récupérer à leur niveau une arithmétique adéquate et à démontrer certaines lois de réciprocité. Au passage, il appliqua ces idées au problème de Fermat. On peut en effet factoriser l'équation
En utilisant l'arithmétique développée pour les nombres cyclotomiques, Kummer montra le théorème de Fermat pour toute une famille d'exposants, en particulier pour tous les exposants plus petits que 100 (sauf trois d'entre eux qui furent étudiés un peu plus tard). Ce résultat spectaculaire lui valut un prix de l'Académie des sciences de Paris, mais il affirma toujours que ce théorème n'était qu'une curiosité, alors que les lois de réciprocité étaient le pinacle de la théorie des nombres. Il faut souligner qu'à la suite des travaux de Kummer, des mathématiciens comme Richard Dedekind ou Leopold Kronecker développèrent l'arithmétique de nombres complexes (algébriques) généraux. Leurs recherches eurent un très grand retentissement au-delà de la théorie des nombres. Par exemple, c'est à eux que nous devons les notions maintenant familières de corps et d'idéal.
C'est surtout au cours du 19ème siècle que la renommée du théorème de Fermat se développa. C'est d'ailleurs vrai de la théorie des nombres dans son ensemble. Son charme particulier, écrivait Gauss, vient de la simplicité des énoncés jointe à la difficulté des preuves : une réflexion qui semble faite tout exprès pour le théorème de Fermat. Le problème fut donc souvent choisi jusqu'à notre époque comme exemple dans des popularisations des mathématiques ou dans les ouvrages d'enseignements et Andrew Wiles dit d'ailleurs que c'est ainsi qu'il s'est intéressé aux mathématiques lorsqu'il était enfant.
Au cours du 20ème siècle, les méthodes utilisées en théorie des nombres ont beaucoup changé. En 1985, Etienne Fouvry, maintenant à l'université Paris-Sud, utilisa des estimations très difficiles d'analyse pour prouver que, pour une infinité de nombres premiers n, l'équation de Fermat relative à l'exposant n n'a pas de solutions sauf si x, y ou z est divisible par n. Et à peu près à la même époque, Gerd Faltings montra qu'il n'existait qu'un nombre fini de rationnels (x/z, y/z) définis à partir des solutions de l´equation de Fermat. Ce dernier résultat venait d'une nouvelle réinterprétation de l'équation de Fermat, comme celle d'une courbe plane :
Faltings prouva en fait un théorème plus général disant que toute courbe définie par un polynôme à coefficients entiers, et de genre au moins 2, n'a qu'un nombre fini de points à coordonnées rationnelles. Le genre d'une courbe est lié au degré des équations qui la définissent et à ses points singuliers, comme les noeuds et les points de rebroussements. Le résultat de Faltings exigeait tout un arsenal de techniques développées depuis les années 60, qui permettent de faire de la géométrie non seulement sur le corps des réels ou des complexes, mais sur des corps quelconques (celui des rationnels par exemple) et même sur des structures plus compliquées. Malheureusement, ce résultat n'était pas effectif, c'est-à-dire qu'on ne savait pas du tout comment borner la taille des éventuelles solutions, ce qui aurait permis de vérifier à coup sûr, par un calcul sur ordinateur par exemple, qu'il n'y en avait pas pour la courbe liée à Fermat. Depuis quinze ans, les recherches sur une version effective du théorème de Faltings se sont d'ailleurs poursuivies.
La démonstration qu'a donnée Wiles repose elle aussi sur une réinterprétation géométrique, mais différente de celle-ci. Dès les années 70, Yves Hellegouarch (université de Caen) avait relié l'équation de Fermat à celle de la courbe
On remarquera qu'ici l'équation de Fermat n'est pas interprétée directement comme celle d'une courbe : chaque solution éventuelle de l'équation de Fermat définit les coefficients d'une courbe particulière, qu'on appelle une courbe elliptique. Au milieu des années 80, il fut montré que si le théorème de Fermat était faux, c'est-à-dire s'il existait une courbe elliptique avec les coefficients comme ci-dessus, elle contredirait une conjecture très importante en mathématiques, la conjecture de Shimura-Taniyama-Weil (STW). Cette conjecture établit un dictionnaire entre les courbes elliptiques et des fonctions dites "modulaires" ; ces dernières ressemblent un peu aux fonctions cosinus et sinus, en particulier elles vérifient certaines propriétés de périodicité. Le lien entre la conjecture STW et le théorème de Fermat n'est pas du tout facile ; Ken Ribet, qui l'a établi en 1986, a d'ailleurs reçu pour cela ... le prix Fermat. Comme dans les autres situations déjà mentionnées, le fait d'intégrer le problème de Fermat dans un cadre apparemment beaucoup plus difficile constitue quand même une avancée, parce qu'on dispose alors de tout un outillage développé pour ce cadre.
Mais la preuve de la conjecture STW semblait inaccessible : c'est elle pourtant qu'a obtenue Andrew Wiles, avec l'aide de Richard Taylor, dans un cas particulier suffisant pour le théorème de Fermat. Elle repose en particulier sur une étude d'une famille de symétries particulières de la courbe elliptique, qui suffisent à la caractériser ; Wiles parvint à réaliser une de ces symétries comme une symétrie associée à une fonction modulaire, puis, par une théorie difficile de déformations, à rattraper l'ensemble de la famille. Là encore, la stratégie développée a beaucoup d'intérêt en elle-même et donne l'espoir de mieux comprendre les relations profondes entre des objets issus de la géométrie algébrique et des fonctions spéciales comme les fonctions modulaires.
Il est bien sûr possible que d'autres démonstrations, plus simples peut-être, du théorème de Fermat, soient trouvées dans les prochaines années. Quoi qu'il en soit, la fin de la saga Fermat n'est pas la fin de la théorie des nombres : outre les approches évoquées au cours de ce récit, et dont l'étude se poursuit activement, bien d'autres problèmes, théoriques ou plus appliqués, restent à résoudre.
Karim.Belabas,
Catherine
Goldstein
Laboratoire de Mathématique d'Orsay, Bâtiment 425
Ce sont les nombres de la forme a + i b où a et b sont deux réels et i est un symbole qui vérifie les propriétés habituelles de l'addition et de la multiplication ainsi que la curieuse propriété i2 = -1. De même que les réels forment une droite, les nombres complexes forment un plan : le nombre a + i b est associé au point du plan de coordonnées (a,b).
Les nombres complexes ont été introduits pour donner une racine carrée aux nombres négatifs. Ils permettent aussi d'extraire des racines n-ièmes : pour tout nombre complexe z non nul, l'équation

Si a et b sont des réels fixés, les points P=(x,y) du plan solutions de l'équation y2= x(x-a)(x-b) définissent une courbe dans le plan, appelée courbe elliptique si a et b sont distincts et non nuls.
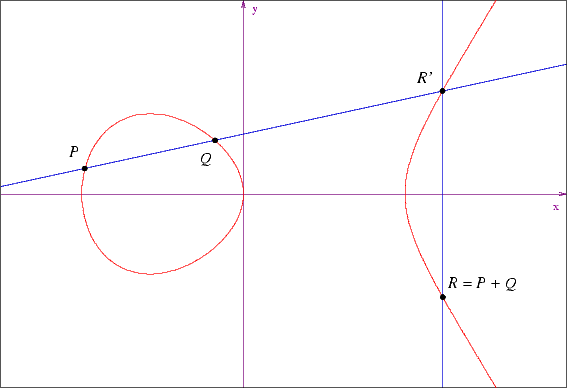
Si P et Q sont deux points d'une même courbe elliptique, la
droite passant par P et Q coupe la courbe en un troisième point
R'. La droite verticale passant par R' coupe la courbe en un
second point R (voir figure). Dans la cas particulier où
P=Q, il faut interpréter la droite passant par P et
Q comme étant la tangente en P. Si P et Q sont
sur une même verticale, le point R' est "à l'infini", et on convient
que R = R'.
Il faudrait donc compléter la courbe par un point à l'infini. C'est plus clair
dans le cadre de la géométrie projective: on s'intéresse aux
(x,y,z) solutions de
y2 z = x(x-az)(x-bz), en identifiant les points se trouvant
sur une même droite passant par 0. Les points "habituels" correspondent à
z non nul, et les points à l'infini à z = 0.
Si P et Q ont des coordonnées rationnelles, R aussi (si l'équation de la courbe est à coefficients rationnels). Ainsi, a partir d'un point rationnel, on en construit de nouveaux. Mordell a prouvé que tous les points rationnels s'obtiennent par ce procédé a partir d'un nombre fini d'entre eux. Il a conjecturé que sur une courbe ou ce type de construction n'est pas disponible, il n'y a qu'un nombre fini de points rationnels. C'est cette conjecture que Faltings a prouvée en 1983.

On cherche les triplets x, y, z de rationnels vérifiant x2 + y2 = z2, tels que l'aire du triangle rectangle de coté x, y, z (= xy / 2 ) soit un entier n. On dit alors que n est un nombre congruent. 6 est congruent (32 + 42 = 52, 4 x 3 / 2 = 6). Fermat a montré que 1 n'est pas congruent - c'est équivalent au théorème de Fermat pour l'exposant 4 ! On montre que n est congruent si et seulement si la courbe elliptique y2 = x3 - n2 x a une infinité de points à coordonnées rationnelles (ceci ne contredit pas le théorème de Faltings puisqu'une courbe elliptique est de genre 1 < 2). À partir de l'un de ces points, on obtient un triplet convenable.
Grâce à toute la mécanique évoquée dans le texte, Tunnel (1983) a donné un critère simple pour décider si un entier n est congruent. La réciproque («si le critère est vérifié, n est-il congruent ?») n'est pas entièrement résolue puisqu'elle dépend encore d'une autre conjecture célèbre (BSD), formulée par Birch et Swinnerton-Dyer dans les années 60, qui prédit en particulier que la courbe elliptique E a une infinité de points rationnels si et seulement si une certaine fonction modulaire s'annule en 1 (et bien plus que cela).
Sans BSD, la théorie ne garantit pas l'existence d'un point, mais permet d'essayer de le construire. S'il existe, c'est gagné ! Pour n = 157, voici la plus petite solution, qu'une recherche naïve n'a aucune chance de découvrir :
On fixe un entier N et on regroupe tous les entiers qui diffèrent d'un multiple de N : on écrit x=y (mod N) (lire x congru à y modulo N) pour «x et y sont dans la même boîte». Par exemple si N=2, on se retrouve avec deux grandes boîtes : les entiers pairs (= 0 (mod 2)) et les impairs (= 1 (mod 2)). Les boîtes sont appelées des entiers modulo N.
On convient que l'on a le droit d'additionner ou de multiplier deux boîtes en effectuant l'opération sur un nombre de chaque boîte, et en regardant où tombe le résultat. Par exemple, si N=60, 40+30=10 (mod 60); autrement dit, cette opération additionne des minutes en oubliant les heures.
Parfois, on peut même faire des divisions ! Voici comment calculer 1/2 si N = 5 : on remarque que 6 = 2x3 = 1 (mod 5) donc 3 = 1/2 (mod 5) ; finalement, diviser par 2, c'est multiplier par 3. Si N n'est pas premier, la division n'est pas toujours possible; par exemple, si N = 6, l'équation 4 x X = 1 (mod 6) n'a pas de solution puisque le membre de gauche est pair, et celui de droite impair. Ceci est du au fait que 4 et 6 ont un diviseur commun : 2.
Un système cryptologique transforme un message pour protéger la confidentialité des données qu'il contient, ou pour prouver que son expéditeur est bien celui qu'il prétend être. Les codes historiques, comme le «Jules Cesar» (on permute les lettres uniformément ; par exemple A -> B, B -> C, etc.) ou les clés secrètes souffrent du défaut suivant : chiffrer et déchiffrer un message sont des opérations symétriques. Si l'espion qui envoie les message est pris, et avec lui le code, les messages codés deviennent lisibles.
Un système à clé publique comme RSA (du nom de ses inventeurs Rivest, Shamir et Adleman en 1977), qui est de loin le plus utilisé de nos jours dans les applications commerciales (par exemple pour assurer la confidentialité des informations qu'on envoie sur Internet, ou pour transmettre des clés secrètes destinées à un autre protocole cryptographique), résout ce problème en fonctionnant avec deux clés : l'une, publique, permet à n'importe qui de coder un message, l'autre, secrète, permet au destinataire de les lire. Le système, très simplifié ici, repose sur le théorème suivant, dû à Euler, et qui généralise un résultat... de Fermat (le «Petit Théorème de Fermat») :
Soit N = pq le produit de deux (grands) nombres premiers distincts, on note f(N) le produit (p-1)(q-1). Si c (comme chiffrer) et d (comme déchiffrer) sont deux entiers tels que
Si on connaît f(N), il est très facile de calculer des entiers c et d ou même, étant donné c, de calculer d. Soit donc M un message à coder (mis sous forme de nombre inférieur à N). Le message chiffré est C = Mc (mod N). Pour le déchiffrer, on calcule
Si on veut «signer» un message, il suffit de lui appliquer sa clé secrète et le destinataire n'a qu'à appliquer votre clé publique pour vérifier qu'il obtient bien un message intelligible, et que vous en êtes donc l'auteur puisque vous disposez de la clé secrète. Pratiquement, on envoie C = Md (mod N) et le récepteur déchiffre en calculant Cc = M comme ci-dessus.
La force du système est qu'on ne sait pas calculer d à partir de c et deN sans connaître f(N), ni f(N), sans connaître p et q. Casser RSA revient à savoir factoriser le (grand) entier N.
Le record actuel [Novembre 2000] (233 chiffres, pour un N = pq de forme spéciale) a nécessité l'équivalent de... 58 ans de calculs sur un ordinateur rapide. Le calcul a été réparti sur plusieurs centaines de machines réparties sur plusieurs sites, les résultats intermédiaires étant collectés par Internet ; en pratique, il a pris cinq mois. Pour un N utilisable par RSA, le record [Août 1999] est de 155 chiffres pour un temps comparable.
Factoriser un nombre de 300 chiffres apparaît totalement hors de portée des méthodes actuelles, même avec les moyens déraisonnables indiqués ci-dessus. C'était le cas des nombres de 200 chiffres il y a 10 ans... Les ordinateurs se perfectionnent bien sur, mais les algorithmes aussi, il en existe une bonne dizaine et des myriades de variantes. Si on ne sait rien sur le nombre à factoriser (ce n'est pas le cas d'un entier RSA puisqu'il est produit de seulement deux premiers, de tailles comparables), il faut choisir une stratégie de recherche en essayant (successivement ou en parallèle) plusieurs méthodes différentes.
L'une d'entre elles (due à Hendrik Lenstra) utilise des courbes elliptiques et est très efficace pour trouver de «petits» facteurs (disons, jusqu'à 40 chiffres, elle ne s'applique donc pas à un entier RSA). Si N est premier, on peut donner un sens à l'expression «courbe elliptique modulo N», et aux formules d'addition de points dont les coordonnées sont des entiers modulo N. Si N est quelconque, on peut faire comme s'il était premier et essayer de calculer. Sauf que maintenant, la division n'étant pas toujours possible, on finira par obtenir une erreur à force d'additionner des points sur des courbes (sans garantie, mais avec une probabilité d'autant plus forte qu'un facteur de N est «petit»). Cette erreur fournit un facteur de N. Notons que déterminer un facteur de 40 chiffres par une méthode naïve (par exemple, essayer de diviser par les nombres premiers successifs : 2, 3, 5, ...) nécessiterait plusieurs milliards d'années.
Des milliers de sites sont consacrés à Fermat ou son "théorème". Consultez un moteur de recherche! Par exemple Google.
Une introduction à la cryptographie :
Biographies en ligne de mathématiciens : [en Anglais]