TP 3 : Factorisation LU d'une matrice pleine
1. Introduction
Le but de ce TP est d'implémenter la factorisation LU d'une matrice pleine, ainsi que la résolution LU.
Question 1
Coder la résolution d'un système linéaire triangulaire inférieur, le tester sur un exemple simple.
Question 2
Coder la méthode du pivot de Gauss, la tester sur la matrice donnée ci-dessous
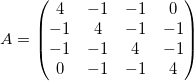
avec le second membre
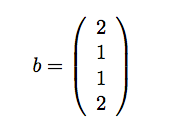
Le résultat que vous devriez obtenir est
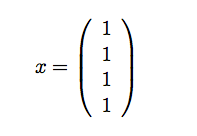
Question 3
Implémenter l'algorithme de factorisation LU et validez-le sur la matrice donnée ci-dessous
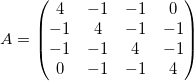
Le résultat que vous devriez obtenir est
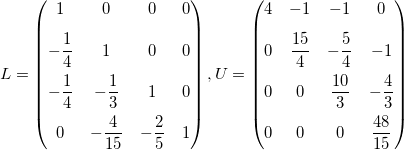
Question 4
Générer une matrice aléatoire de taille n (par exemple 10) et vérifier l'identité A = L U, par exemple en calculant la norme infinie de A - L U. Pour la manipulation des fonctions aléatoires, les fonctions C srand et rand peuvent être utilisées :
! pour fixer a la main un "random seed" de votre choix call srand(103) ! pour utiliser le temps comme random seed : call srand(time()) ! ensuite rand() renvoie un nombre aleatoire entre 0 et 1 x = rand()
La fonction srand sert à initialiser le générateur aléatoire avec un entier appelé "random seed" et doit être placée au début du programme principal. Si le même "random seed" est utilisé, la suite aléatoire sera la même d'une exécution à l'autre.
Question 5
Implémenter une sous-routine pour résoudre A x = b à partir des facteurs L et U précédemment calculés. On suppose ici que L et U sont donnés directement en argument de la sous-routine, et donc on doit résoudre deux systèmes triangulaires successifs puisque :
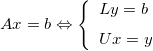
Tester cette sous-routine sur un second membre aléatoire et vérifier que la norme de A x - b est de l'ordre de la précision machine
Question 6
Le but est de cette question est de coder la matrice permettant de résoudre de manière approchée l'équation de Poisson à l'aide d'un schéma différences finies.
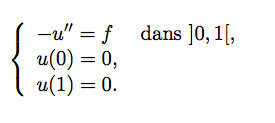
On utilise le schéma différences finies suivant :
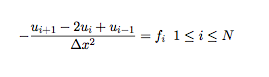
avec N le nombre de points suivant chaque direction et
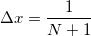
La matrice A associée est tridiagonale (cf. TD d'ANPI) :

Implémenter une sous-routine qui génère la matrice A pour un N donné en argument. Vérifier que la matrice est correcte pour N = 2, 3.
Question 7
Choisissez comme second membre un vecteur F de la forme
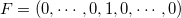
où le 1 est situé au milieu. On cherche alors la solution du système :
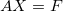
où A est la matrice de la question précédente. Ecrivez la solution dans un fichier et visualisez ensuite le résultat sous gnuplot.
Regardez la solution pour plusieurs valeurs de N, comme N = 20 et N = 40.
Question 8
Coder la méthode du pivot de Gauss avec pivot partiel. Comparer les résultats obtenus avec et sans pivot pour les matrices et les second membres suivants:
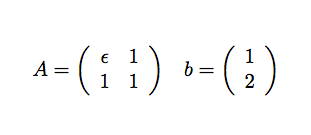
avec
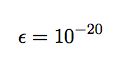
et