|
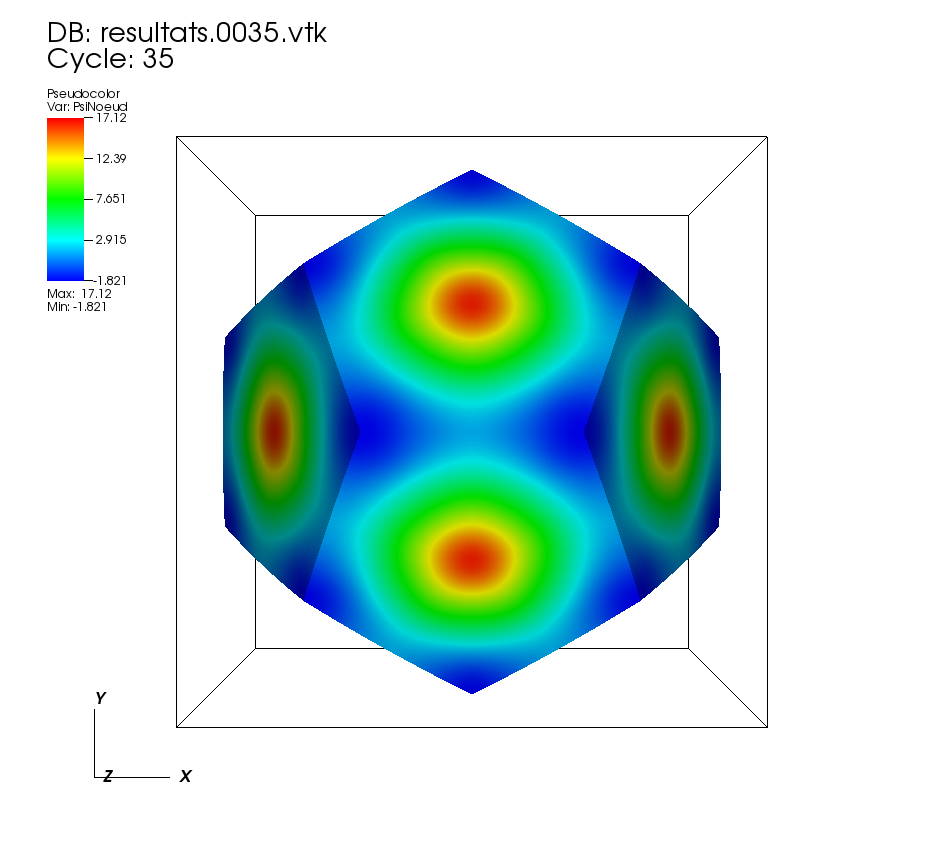
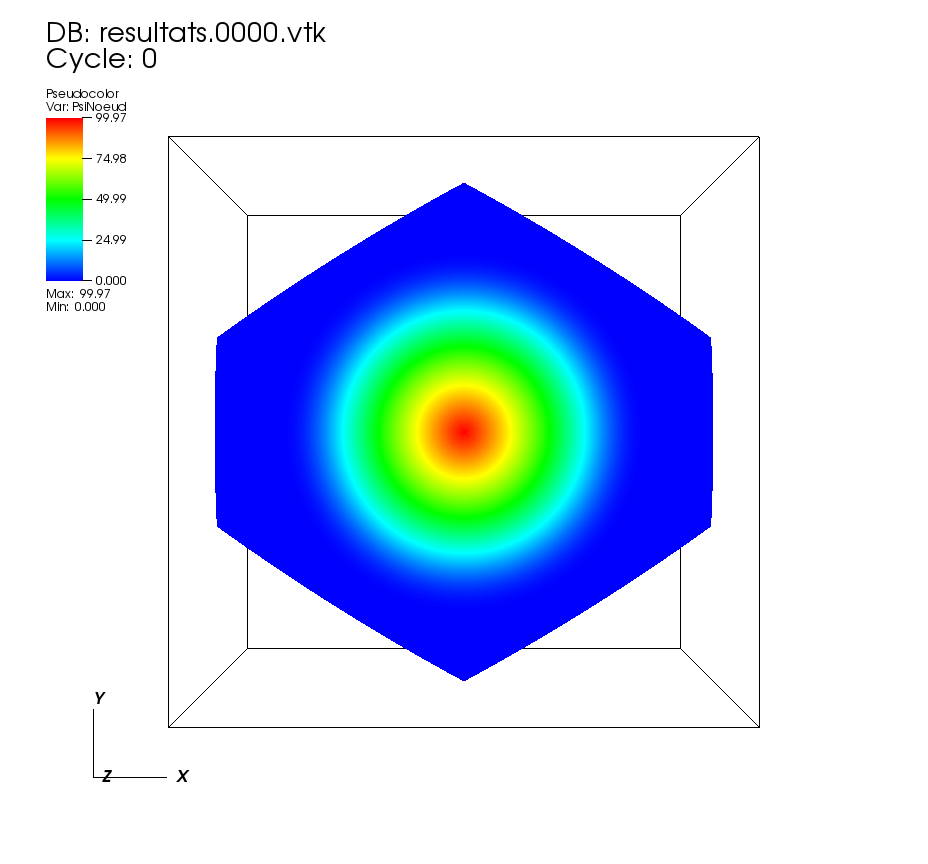
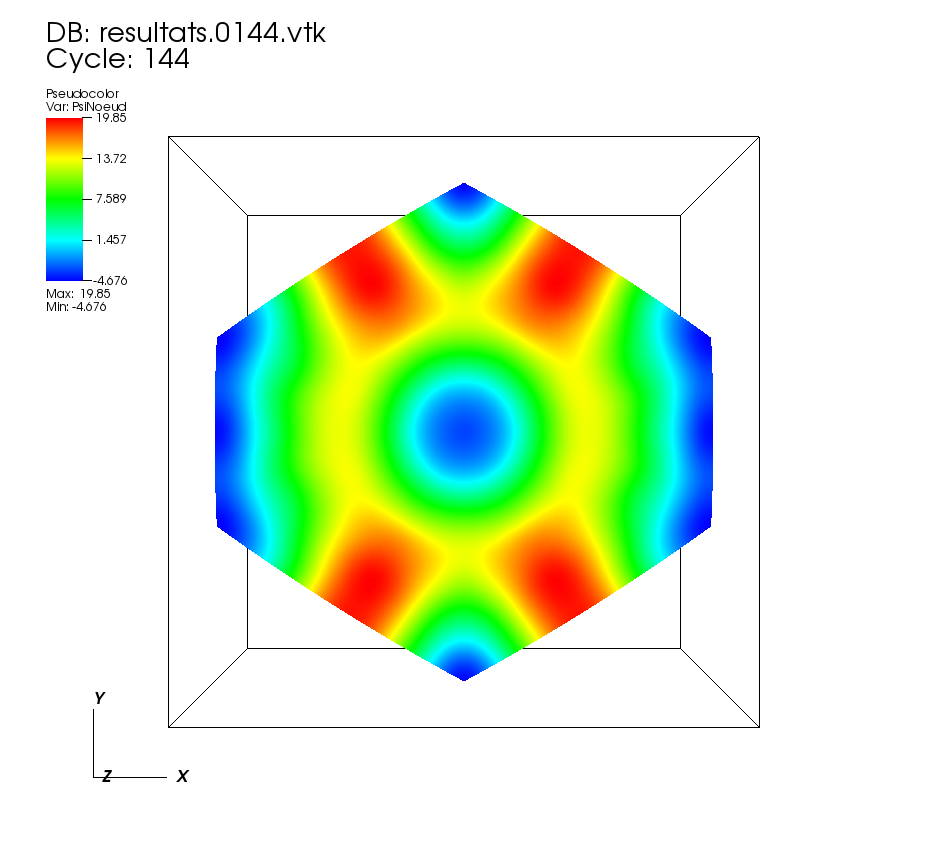
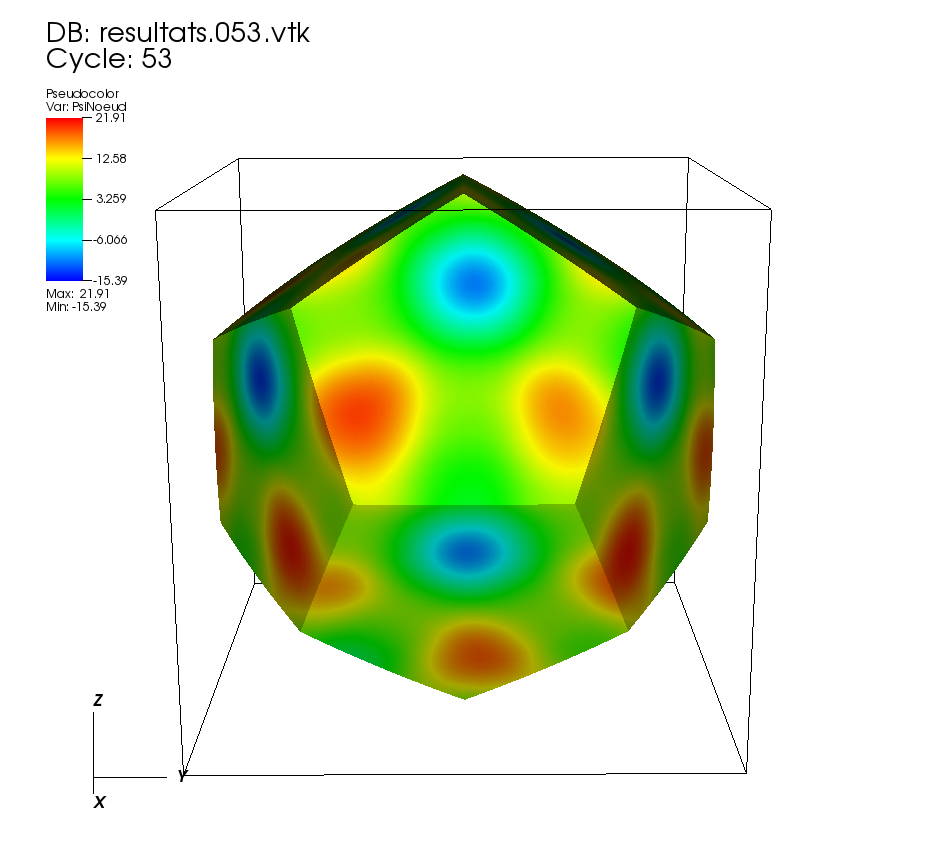
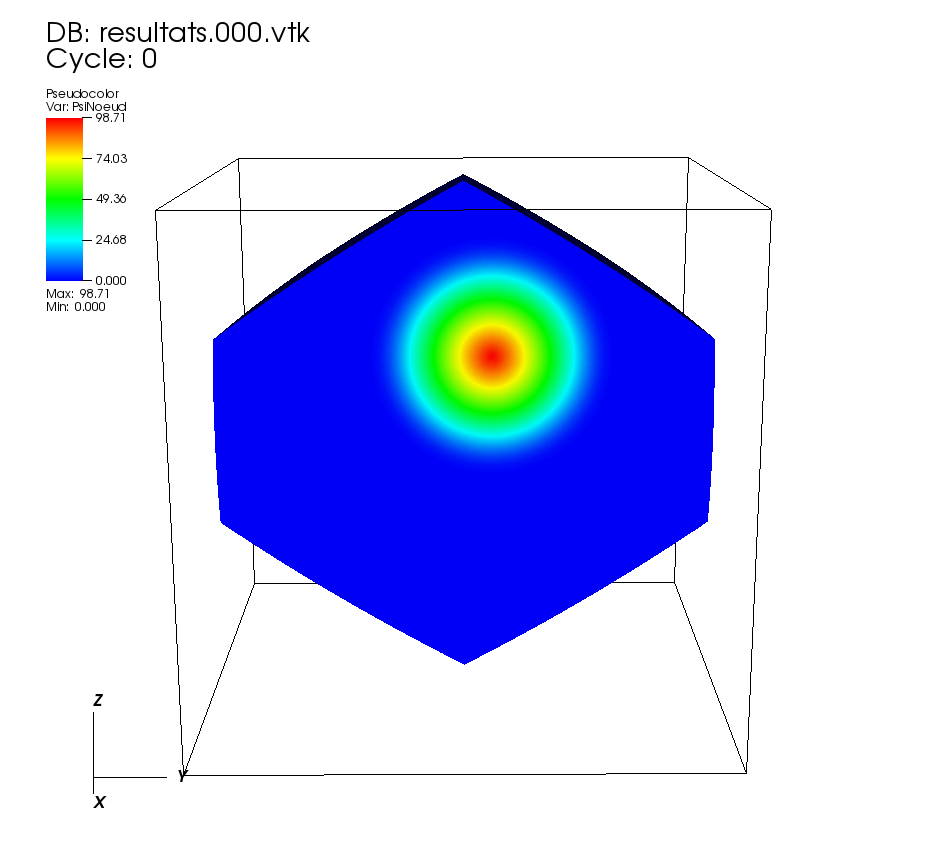
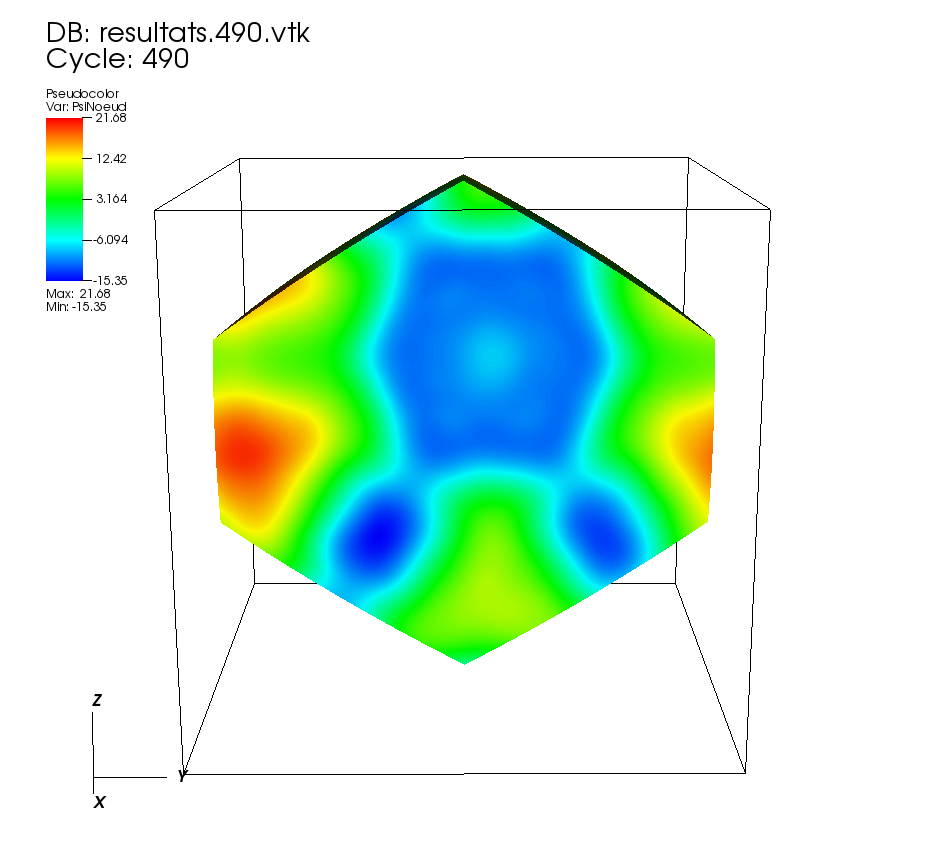
On some faces: •t=0 to t=1 On a cutting plane x=0: •t=0 to t=1 |
|
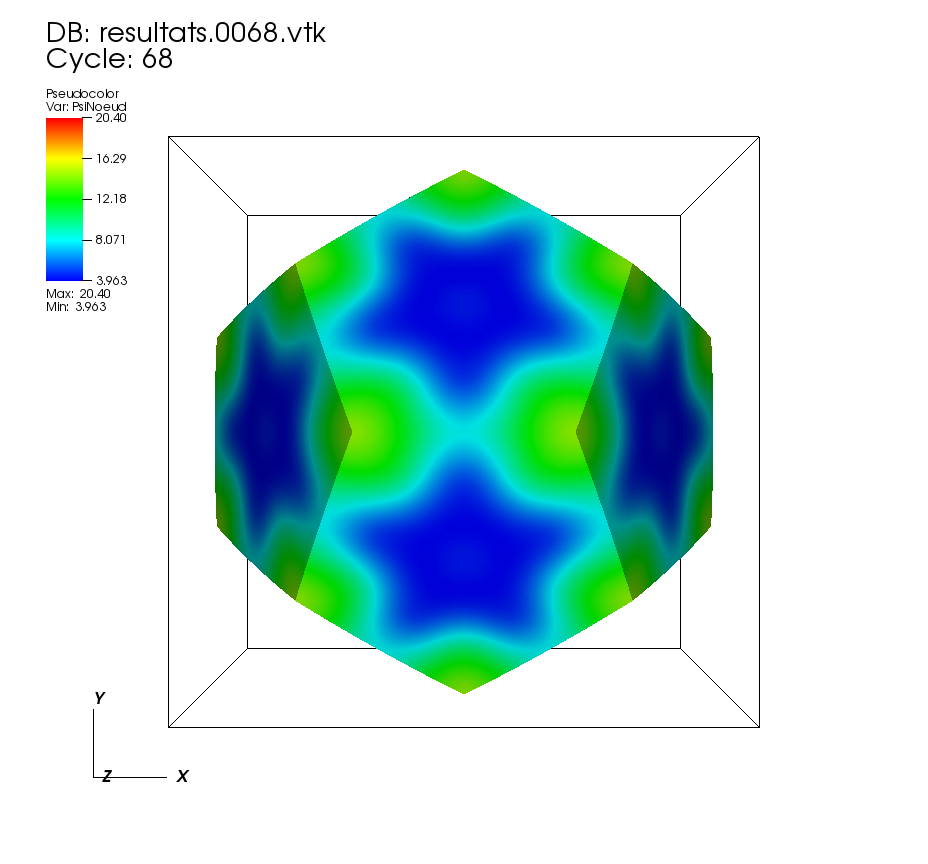
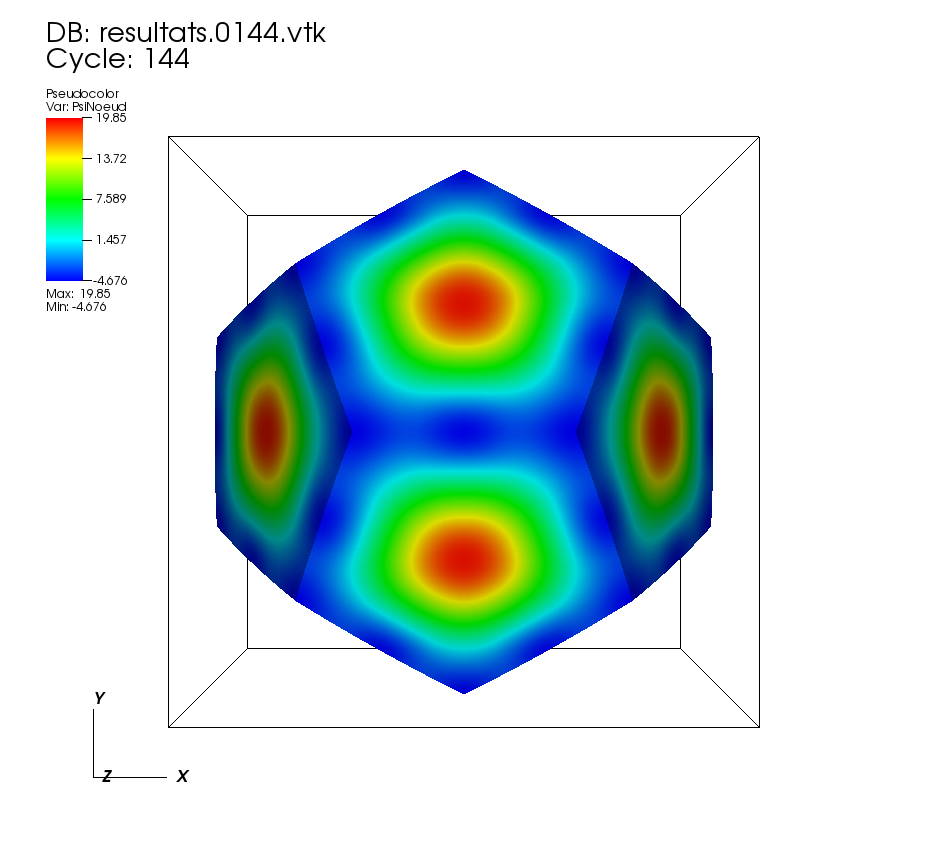
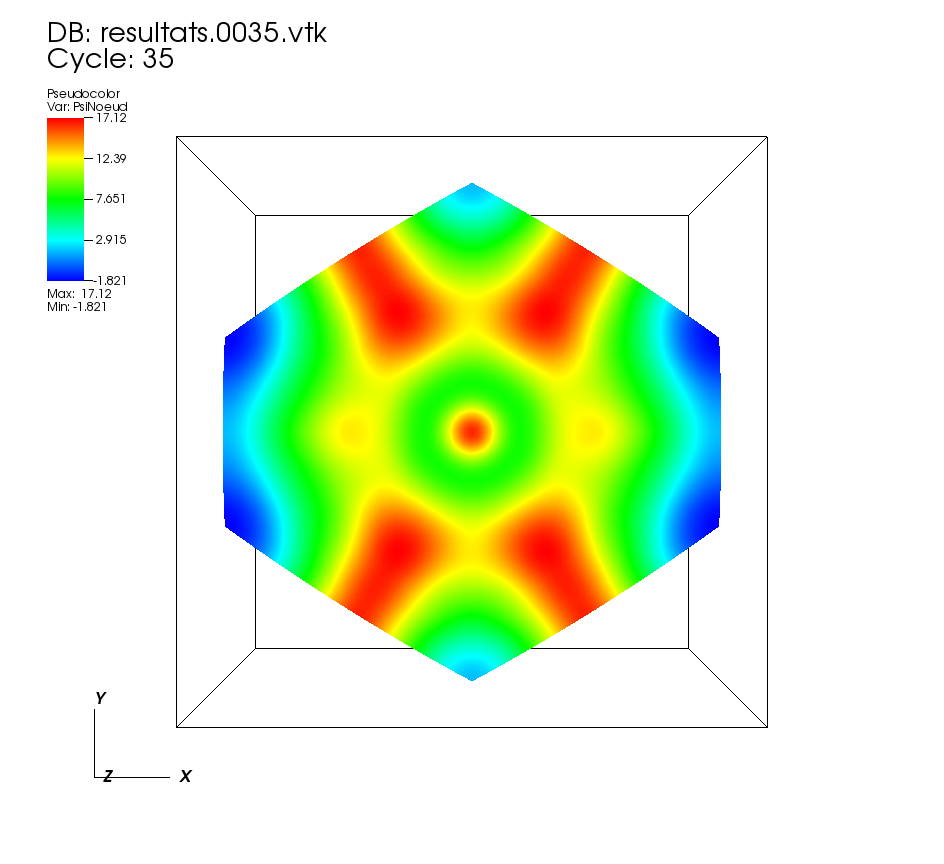
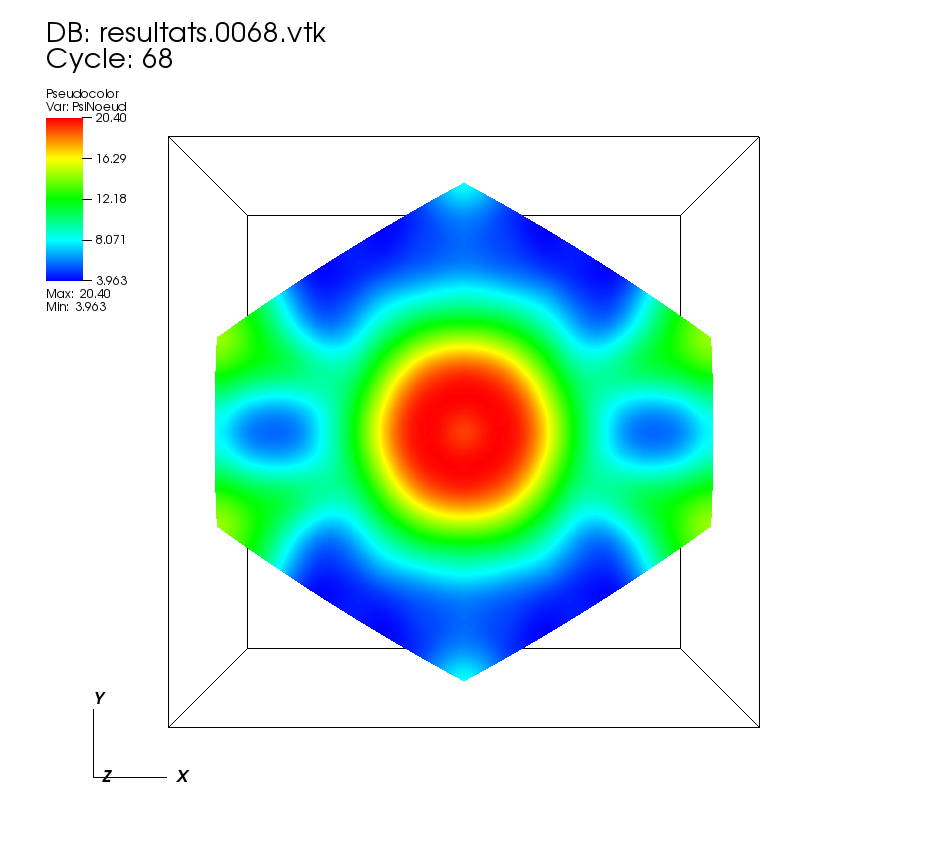
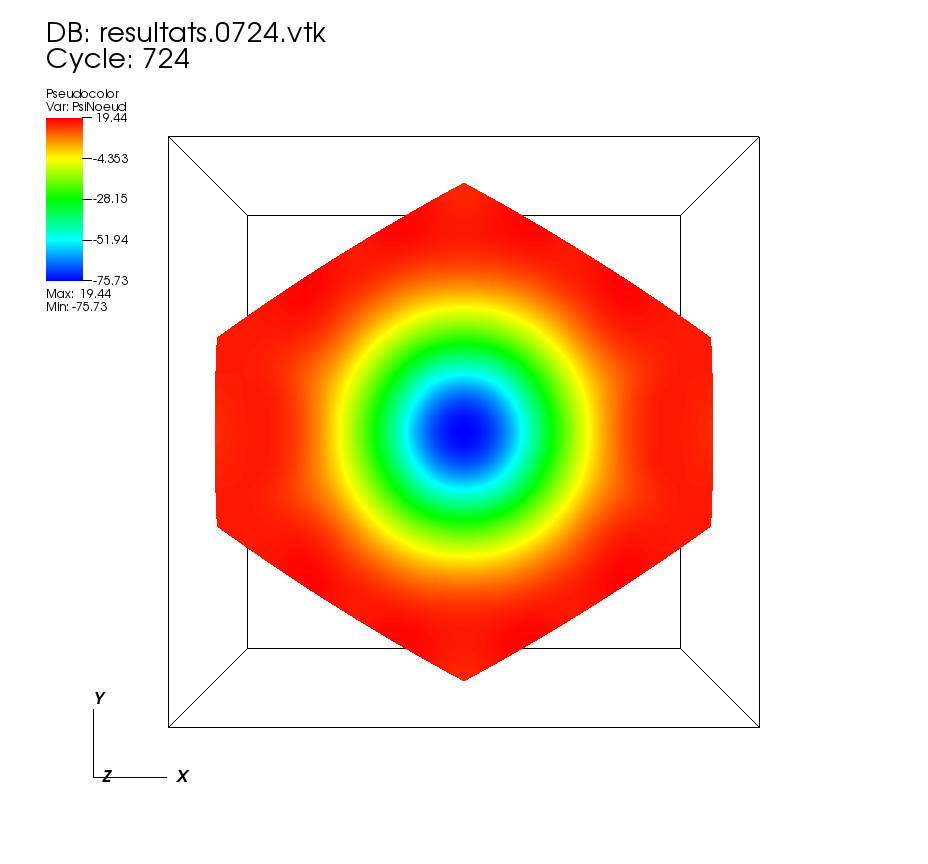
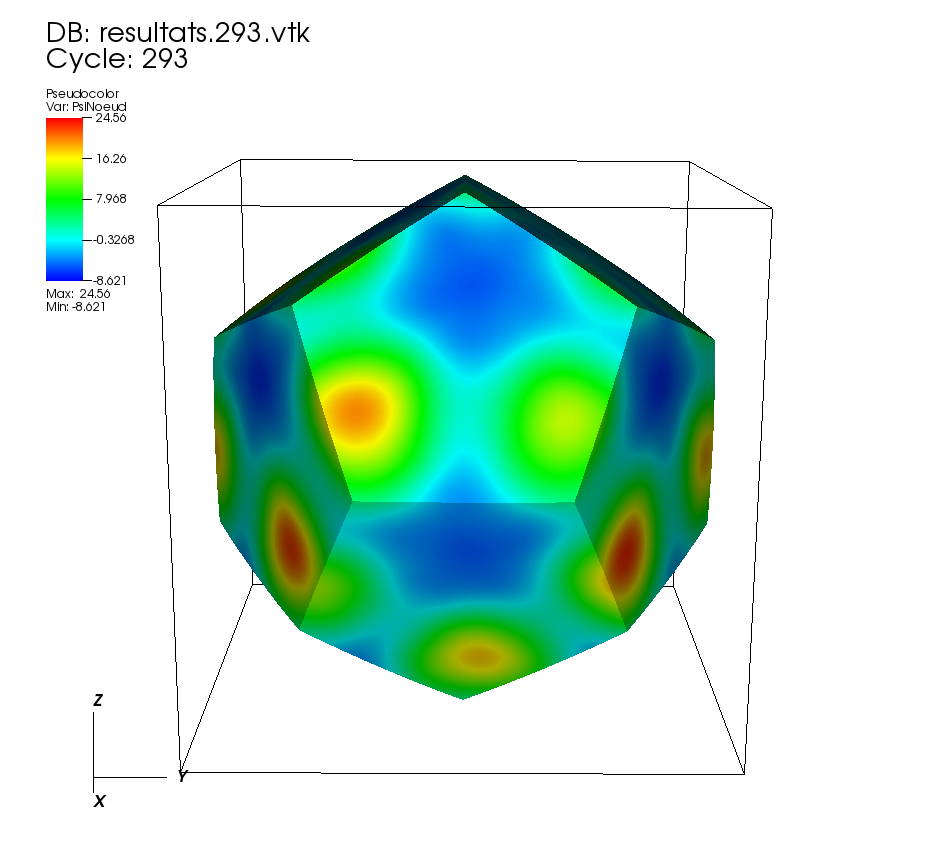
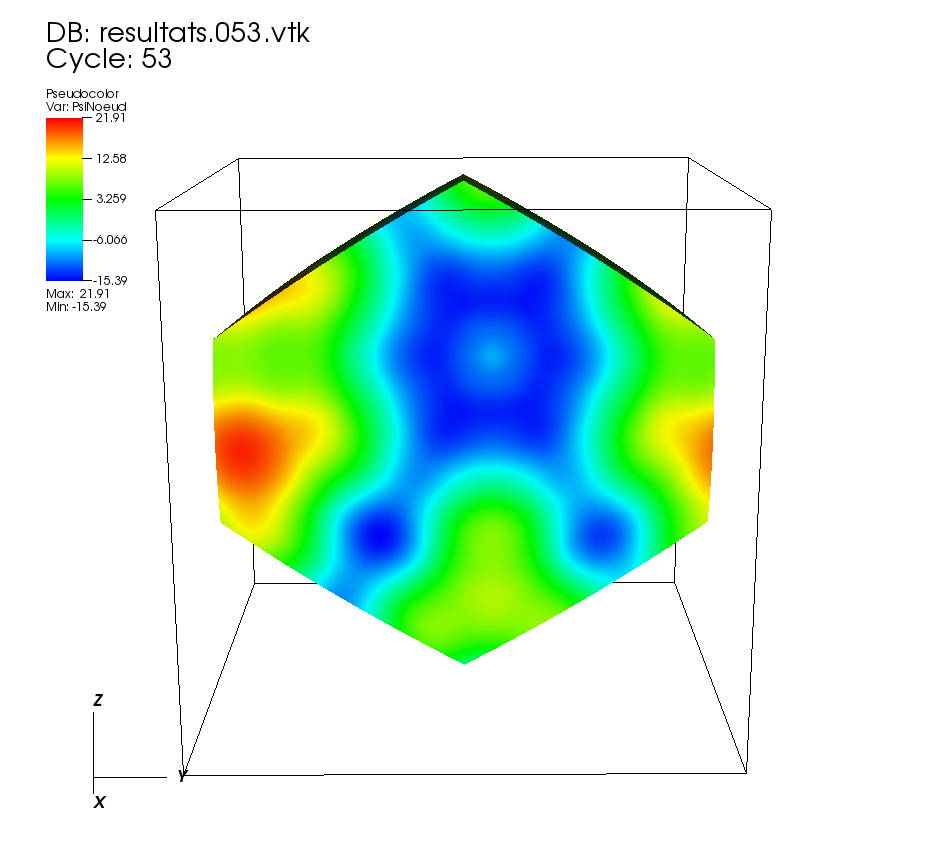
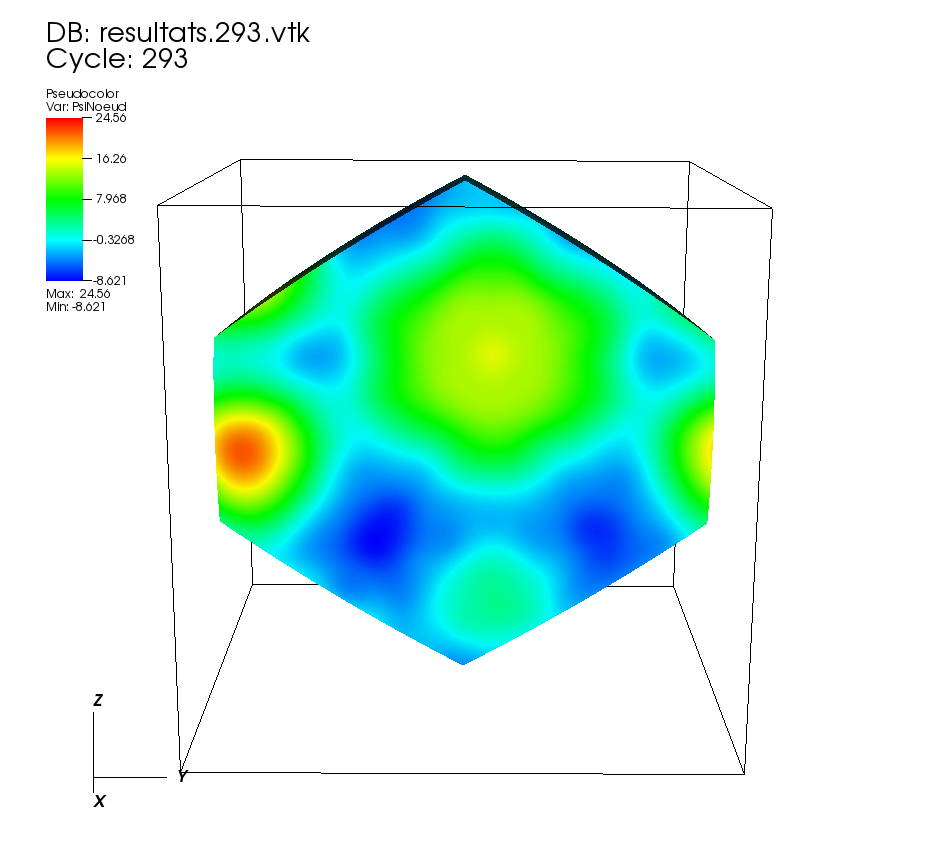
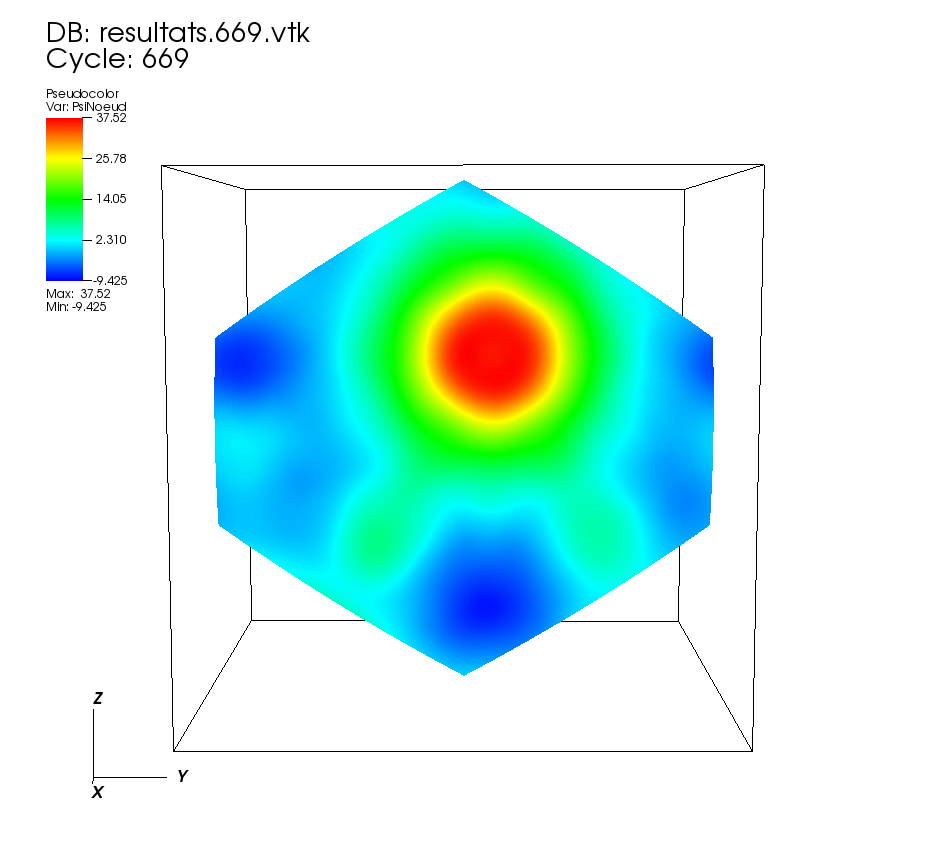
On some faces: • t=0 to t=0.5 •t=0.5 to t=1 On other faces: •t=0 to t=0.5 • t=0.5 to t=1 On a cutting plane z=0: • t=0 to t=0.5 •t=0.5 to t=1 On a cutting plane x=0: •t=0 to 0.5 • t=0.5 to t=1. |
|
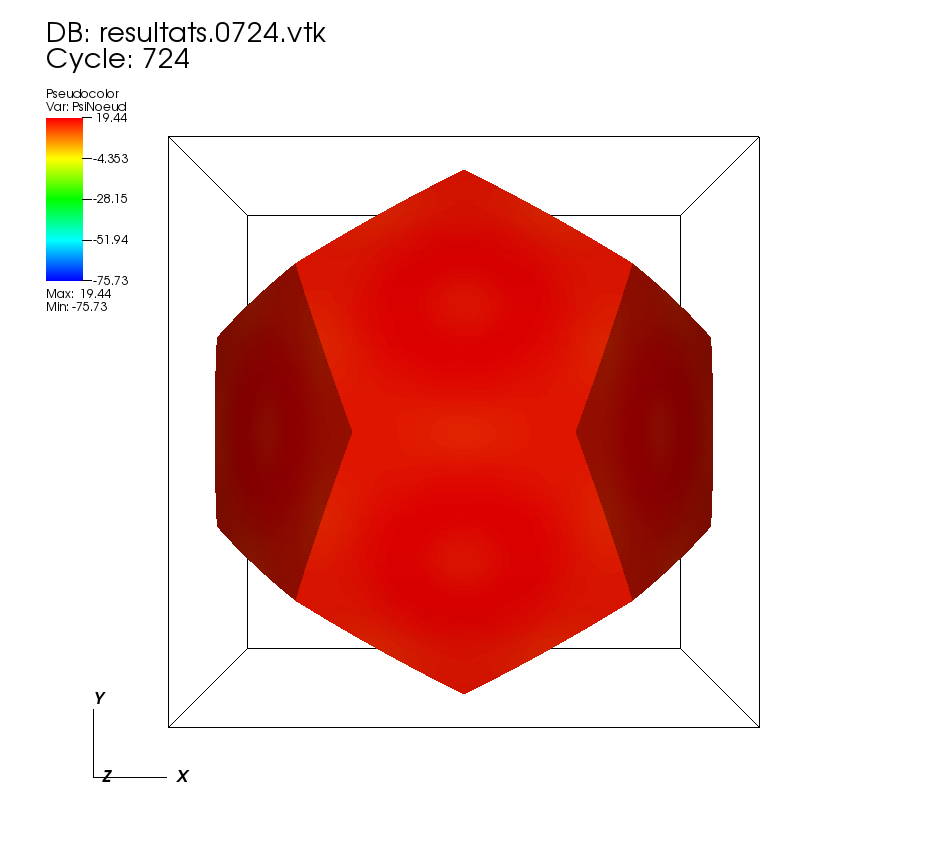
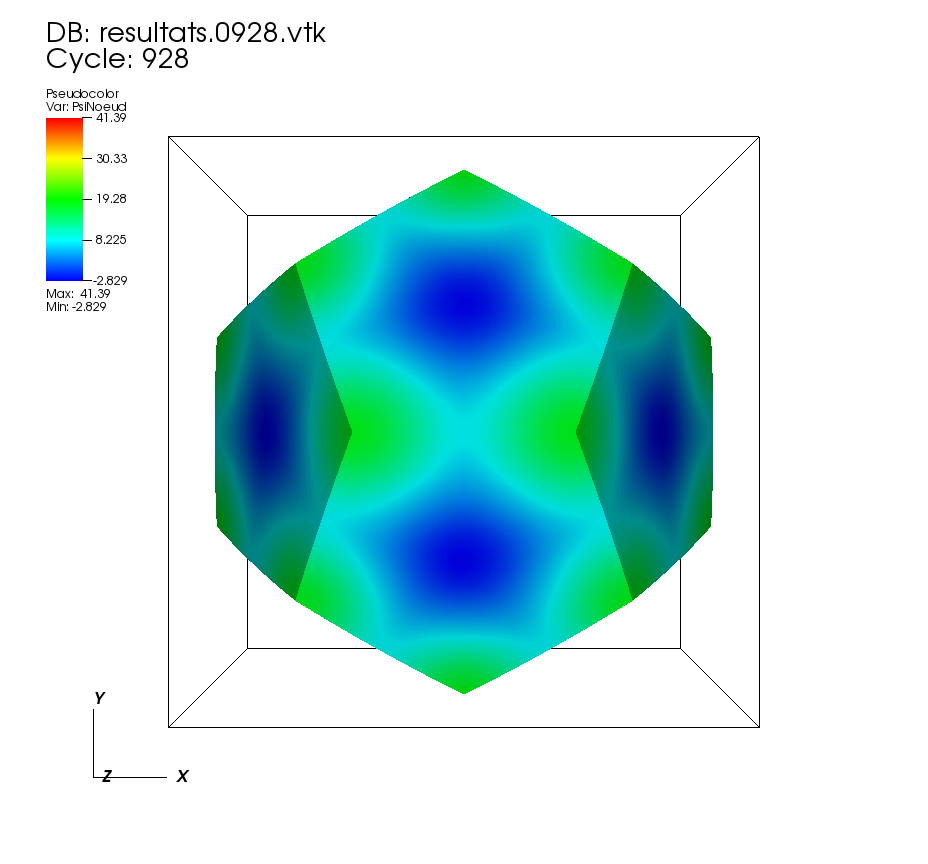
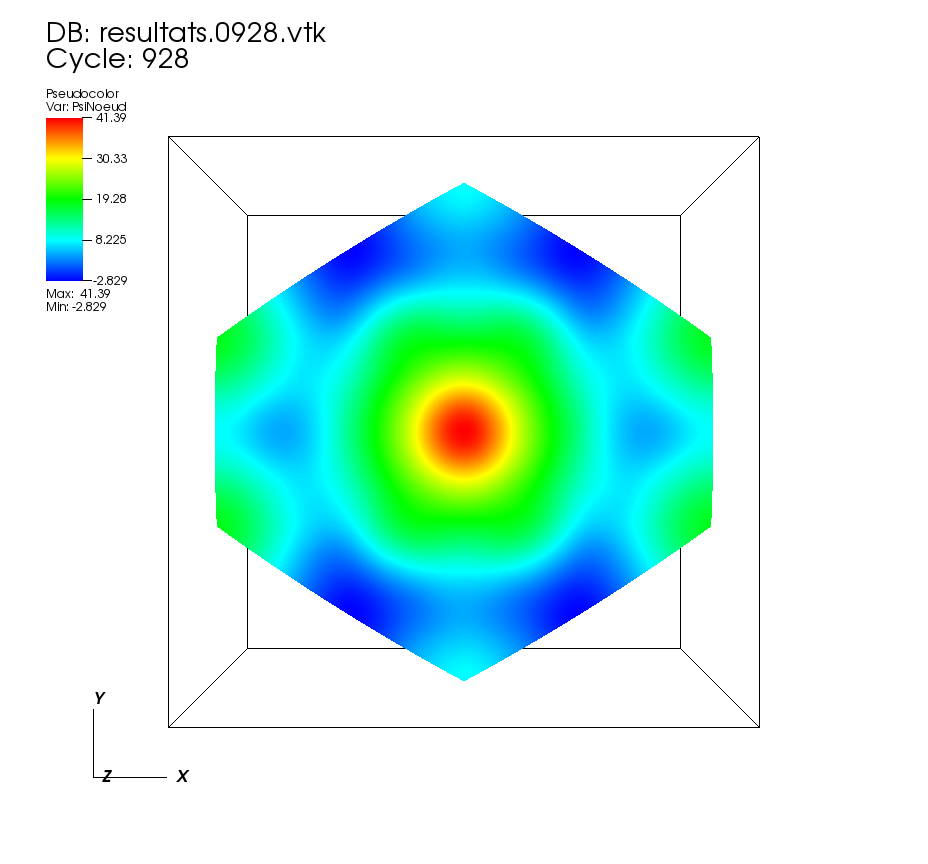
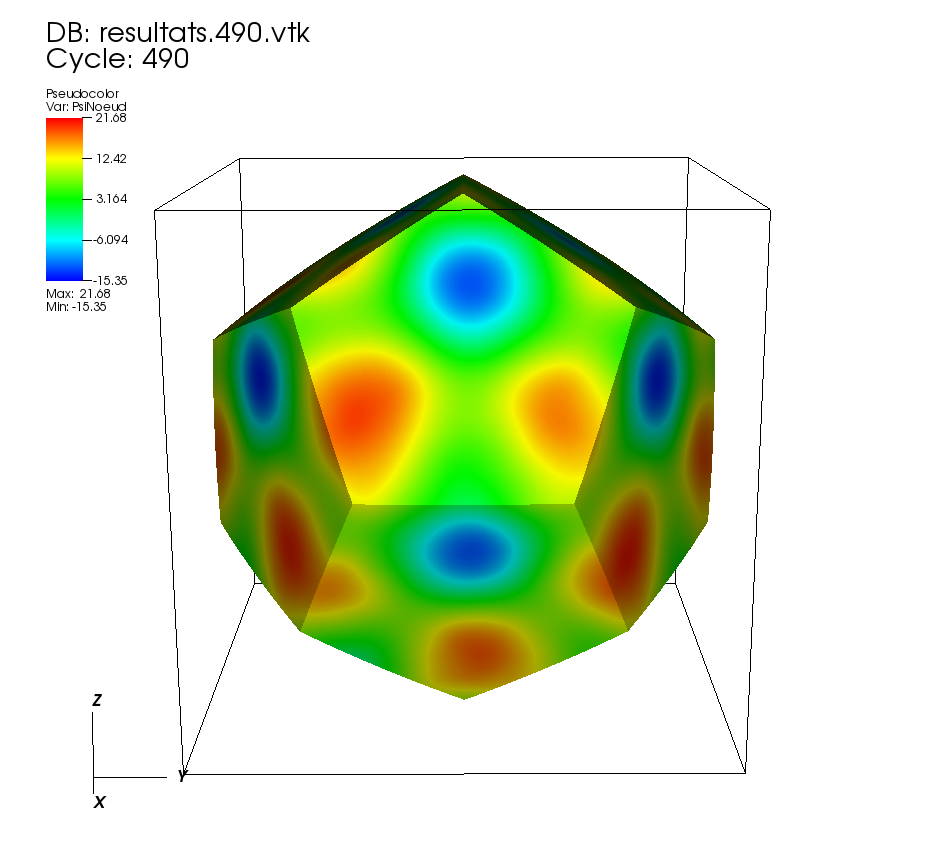
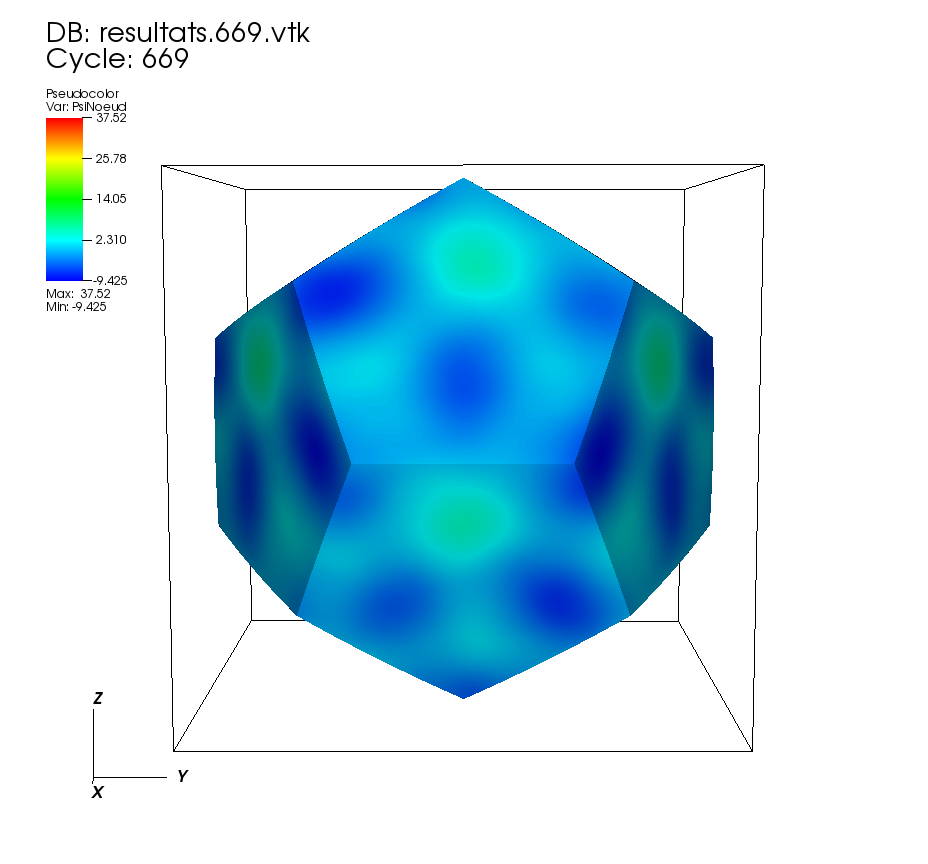
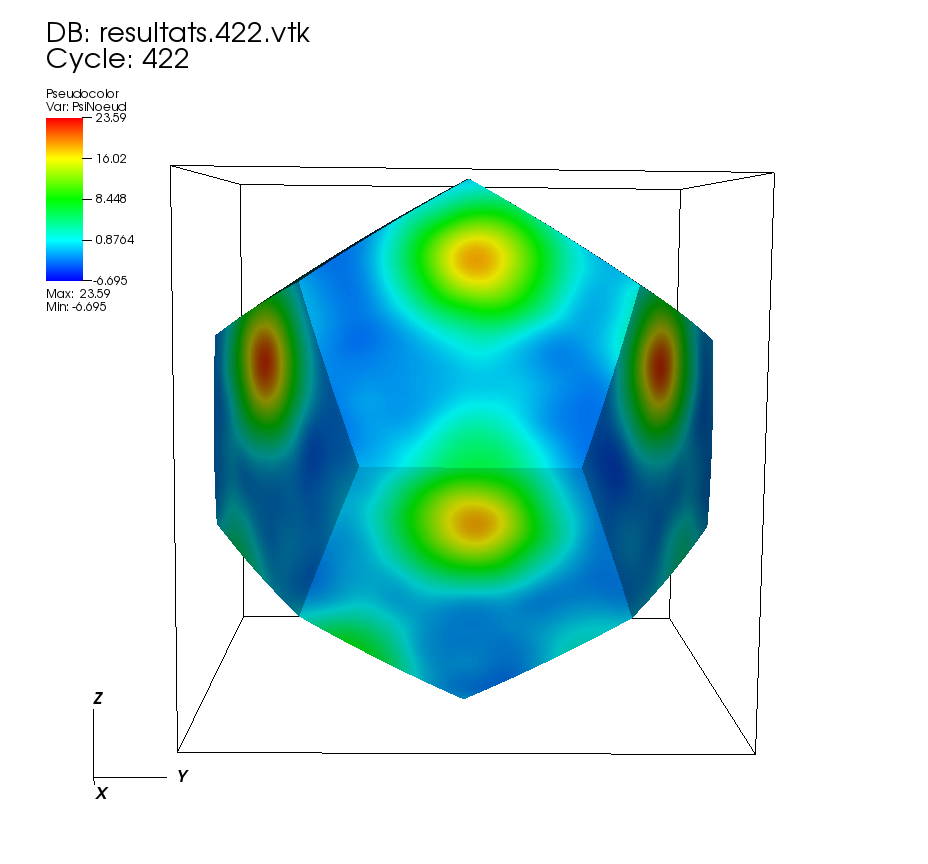
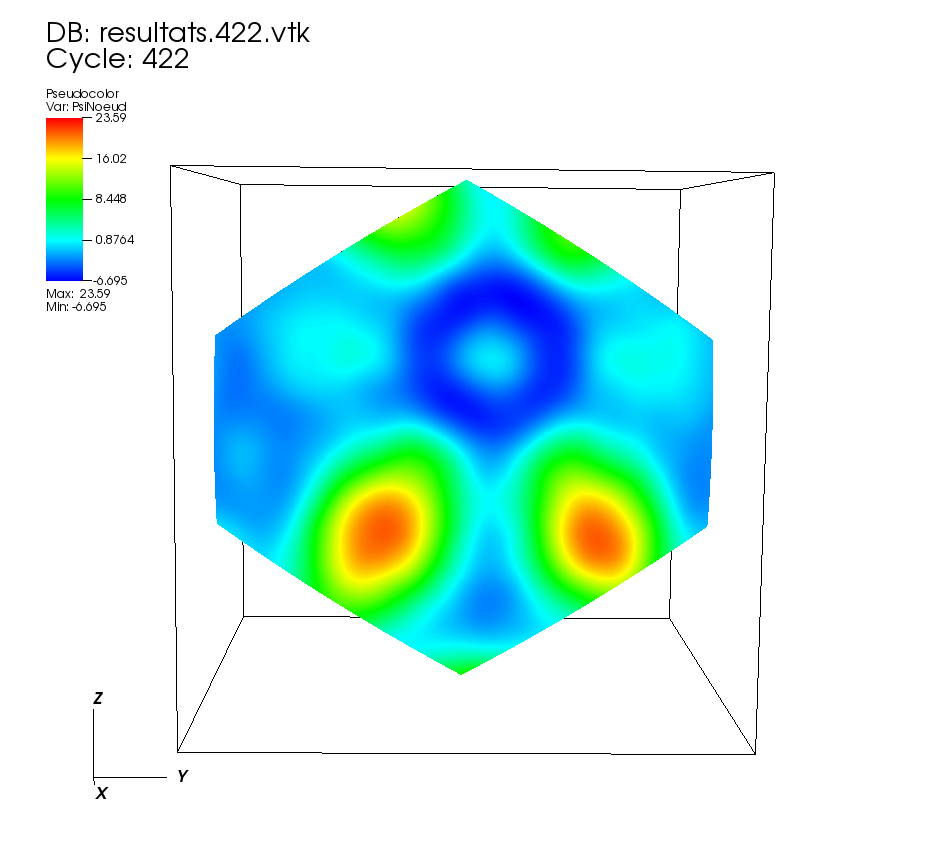
On some faces: • t=0 to t=5 •t=5 to t=10 On a cutting plane: • t=0 to t=5 •t=5 to t=10 On two cutting planes: •t=0 to 0.5 |