Navier-Stokes Cartesian
Download (login and password required)
Documentation doxygen (under development)
Description: NaSCar
(Navier-Stokes Cartesian)
is a research software, written in C and based on Petsc,
to model numerically a wide range a multiphysics problems. The
core is the incompressible Navier-Stokes equations discretized
in space on a Cartesian mesh using Finite Differences and a
temporal integration based on the Chorin and Temam scheme.
Several new approaches to deal with fluid-structure and
fluid-fluid interfaces have been developped including collison
models and high order level set methods together with high
order reinitialization. Elastic structures can be modeled in a
Lagrangian way, or using a fully coupled Eulerian approach
(with Mooney Rivlin model, see last figure).
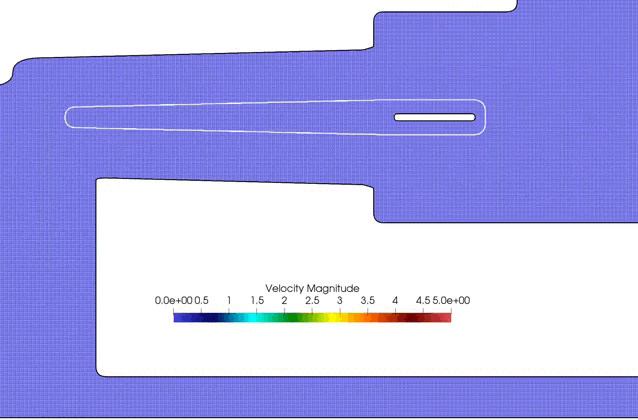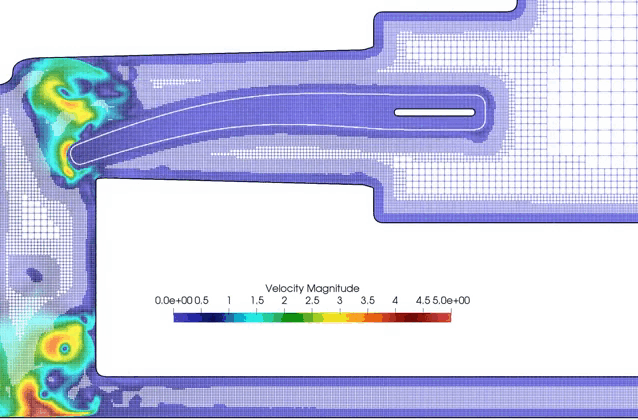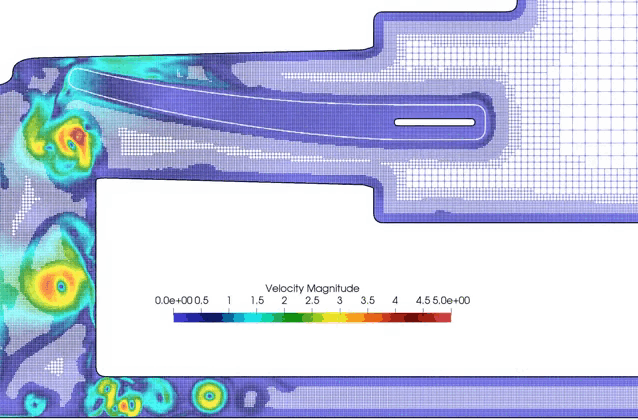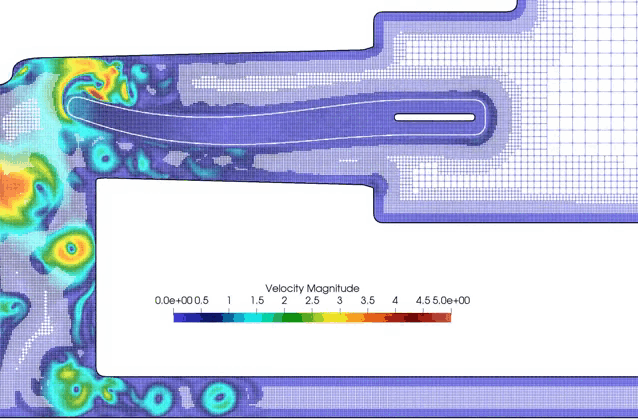
One specificy of the code is toward drag and drop simulation. Any obstacle can be loaded in a simple way (stl, obj, or B-splines user defined bodies), and the simulation can start directly without considering any costly meshing and adaptation steps.
Indeed, all the simulations below are run with the exact same code, with only different input files (*.DAT) defining the geoemtries and physical parameters.
The NaSCar solver will be soon distributed in Open Source.
List of the main fonctionalities
Libraries to generate obstacle profiles
- Import of discrete geometry and regular meshing of this geometry,
- Generation of 3D profiles by B-splines (fish, lines, ...),
- Masks and characteristic functions
Fluid/structure interaction libraries,
- Computation of forces and moments, Euler-quaternion angles,
- One-way: imposed deformation of obstacles and displacement by Newton's laws,
- Two-way: strongly implicit coupling, elastic beam structure, Eulerian elasticity
- Eulerian elasticity: Extrapolation of the backward characteristics
Librairies for structure/structure interaction,
- Lubrication and collision model for spherical and non-spherical obstacles (see TEST4)
Libraries to capture and track interfaces,
- Generation of a level set function from any geometry,
- Transport of the level set function (WENO5 and RK3 TVD),
- Reinitialiszation to the signed distance function (Eikonale with relaxation),
- Contour selection to ensure volume conservation
Libraries to solve the Navier-Stokes equations,
- Incremental projection method of the predictor-corrector type (order 2),
- Adams-Bashford - Crank-Nicholson, Semi-Lagrangian,
- Volume penalization (order 1),
- Immersed boundaries (order 2),
- Hybrid IPC method (order 2),
- Bifluid with surface tension: CSF and GFM methods (order 1), sharp method (order 2),
- LES Smagorinsky-Lilly turbulence model
One specificy of the code is toward drag and drop simulation. Any obstacle can be loaded in a simple way (stl, obj, or B-splines user defined bodies), and the simulation can start directly without considering any costly meshing and adaptation steps.
Indeed, all the simulations below are run with the exact same code, with only different input files (*.DAT) defining the geoemtries and physical parameters.
The NaSCar solver will be soon distributed in Open Source.
List of the main fonctionalities
Libraries to generate obstacle profiles
- Import of discrete geometry and regular meshing of this geometry,
- Generation of 3D profiles by B-splines (fish, lines, ...),
- Masks and characteristic functions
Fluid/structure interaction libraries,
- Computation of forces and moments, Euler-quaternion angles,
- One-way: imposed deformation of obstacles and displacement by Newton's laws,
- Two-way: strongly implicit coupling, elastic beam structure, Eulerian elasticity
- Eulerian elasticity: Extrapolation of the backward characteristics
Librairies for structure/structure interaction,
- Lubrication and collision model for spherical and non-spherical obstacles (see TEST4)
Libraries to capture and track interfaces,
- Generation of a level set function from any geometry,
- Transport of the level set function (WENO5 and RK3 TVD),
- Reinitialiszation to the signed distance function (Eikonale with relaxation),
- Contour selection to ensure volume conservation
Libraries to solve the Navier-Stokes equations,
- Incremental projection method of the predictor-corrector type (order 2),
- Adams-Bashford - Crank-Nicholson, Semi-Lagrangian,
- Volume penalization (order 1),
- Immersed boundaries (order 2),
- Hybrid IPC method (order 2),
- Bifluid with surface tension: CSF and GFM methods (order 1), sharp method (order 2),
- LES Smagorinsky-Lilly turbulence model
Examples of actual
simulations with NaSCar (the movies are built
with paraview)

Boat ride: the boat geometry is given by an obj file

Snake swimming: user defined body shape and swimming law

Dolphin jump: real dolphin shape from stp file with user defined swimming law

Fish swimming with collisions