Séminaire de Théorie Analytique des Nombres et Problèmes
Diophantiens
Indépendance linéaire d'une infinité de valeurs de la fonction zêta de Riemann aux entiers impairs.
Résumé
:
On introduit une série hypergéométrique permettant de construire des
combinaisons linéaires rationnelles de valeurs de la fonction zêta de
Riemann aux entiers impairs.
L'étude arithmétique et asymptotique de ces combinaisons permet d'appliquer
un critère d'indépendance linéaire dû à Y. Nesterenko et de prouver le
résultat suivant : la dimension de l'espace vectoriel engendré sur
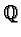par 1 et les n premières valeurs de la fonction zêta aux
entiers impairs croît au moins comme un multiple de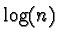 
.
Retour à la
page d'accueil.
stan@math.u-bordeaux.fr