Séminaire de Théorie Analytique des Nombres et Problèmes
Diophantiens
Le 14 juin 2001
Natarajan Saradha (Tata Institute of Fundamental Research)
Some extensions and refinements of a theorem of Sylvester.
Résumé
: An old result of Sylvester says that the greatest prime factor of the
product
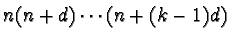exceeds k provided
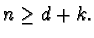Here
n,d,k denote positive integers with
gcd(n,d)=1. In this talk we give
some improvements of this result obtained recently and its application
to
the problem of perfect powers in arithmetic progression.
Retour à la
page d'accueil.
stan@math.u-bordeaux.fr