Soit ![]() .
Un élément du groupe fondamental
.
Un élément du groupe fondamental ![]() est une classe d'homotopie de lacets de base b. Rappelons que
deux lacets
est une classe d'homotopie de lacets de base b. Rappelons que
deux lacets
![]() sont homotopes s'il
existe une application continue
sont homotopes s'il
existe une application continue
![]() satisfaisant les propriétés
satisfaisant les propriétés
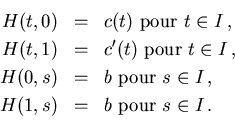
On peut alors faire opérer ![]() sur la fibre p-1(b)
d'un revêtement
sur la fibre p-1(b)
d'un revêtement
![]() ,
en associant à une
classe
,
en associant à une
classe
![]() et à un élément
et à un élément
![]() ,
l'élément
,
l'élément ![]() ,
où
,
où
![]() est un chemin dans E d'origine x relevant c
(noter que
est un chemin dans E d'origine x relevant c
(noter que
![]() ). Cet élément ne dépend pas
des choix effectués pour sa définition.
). Cet élément ne dépend pas
des choix effectués pour sa définition.