


Next: About this document ...
Up: No Title
Previous: Action du groupe fondamental
On a les résultats suivants.
Théorème 1
B possède un revêtement simplement connexe
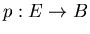 .
Ce revêtement est un revêtement universel de B et le
groupe G des automorphismes de E est isomorphe à
.
Ce revêtement est un revêtement universel de B et le
groupe G des automorphismes de E est isomorphe à
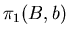 .
Si H est un sous-groupe de G,
.
Si H est un sous-groupe de G,
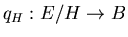 est un revêtement connexe de B, et
est un revêtement connexe de B, et
Théorème 1
Soit
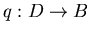 un revêtement de B.
un revêtement de B.
(i) Le groupe 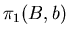 opère sur q-1(b) (voir
paragraphe précédent).
opère sur q-1(b) (voir
paragraphe précédent).
(ii) Pour que D soit connexe, il faut et il suffit que
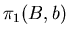 opère transitivement sur q-1(b). Dans ce cas,
si H est le stabilisateur d'un point
opère transitivement sur q-1(b). Dans ce cas,
si H est le stabilisateur d'un point
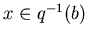 ,
alors
,
alors
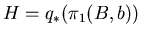 ,
et
,
et
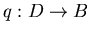 est isomorphe au
revêtement
est isomorphe au
revêtement
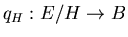 .
.
(iii) Le revêtement
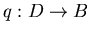 est
isomorphe à un revêtement associé au universel
est
isomorphe à un revêtement associé au universel
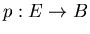 par cette opération de
par cette opération de 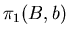 sur
q-1(b).
sur
q-1(b).
(iv) Pour qu'un revêtement
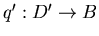 soit isomorphe au revêtement
soit isomorphe au revêtement
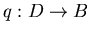 ,
il faut et
il suffit que les opérations de
,
il faut et
il suffit que les opérations de 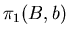 sur q-1(b) et
sur q'-1(b) soient isomorphes.
sur q-1(b) et
sur q'-1(b) soient isomorphes.



Next: About this document ...
Up: No Title
Previous: Action du groupe fondamental
1999-03-17