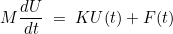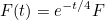Introduction   Curriculum Vitae   Publications   Realisations   Codes   Teaching

Seldon

Seldon is a C++ library for linear algebra (handling vectors, matrices, linear solvers, etc). Here, you can download updated versions of Seldon:

Latest release of Seldon

Additional resources with Seldon:

HTML Documentation
Matrices used for unit tests (folder test/matrix)

Montjoie

Montjoie is a finite element library for solving partial differential equations. It proposes an implementation for wave propagation phenomena. The meshes can be mixed : triangles/quadrilaterals in 2-D, tetrahedra/pyramids/prisms/hexahedra in 3-D. A reduced release of Montjoie can be downloaded here (with only manipulations of meshes)

Montjoie Mesh

Additional resources with Montjoie:

HTML Documentation

Time schemes

Here, you can download a basic implementation in Python of implicit schemes that can be used to solve linear Ordinary Differential Equations (ODEs) (as described in the paper padeSdirk.pdf)

quadrature.py
linear_scheme.py

A linear ode (with dense matrices) is considered in a basic example (class ExampleOde) :

where M and K are dense matrices, with the arbitrary choice

F is a given vector (constant). Padé schemes can be used to solve this linear ode by typing in Python (once linear_scheme.py and quadrature.py have been downloaded) :

        from numpy import *
        from linear_scheme import *
        
        # matrices and source vector
        M = rand(5, 5);
        K = 0.1*rand(5, 5);
        F = rand(5)
        
        # initial condition
        Y0 = rand(5)
        
        # ode to solve
        ex_ode = ExampleOde(M, K, F)
        
        # if you want to use a Pade scheme, you give the order you want
        # type help(PadeScheme) for a detailed help
        # here fourth-order Pade scheme will be construct
        ex_scheme = PadeScheme(4)
        
        # SolveOde returns the final solution at time t=2
        # of the linear ode M dy/dt = K y(t) + F(t)
        # M, K and F are detailed in ex_ode
        # 20 is the number of iterations
        # syntax : SolveOde(t0, tf, N, Y0, scheme, ode)
        # type help(SolveOde) for a detailed help
        Yf = SolveOde(0.0, 2.0, 20, Y0, ex_scheme, ex_ode);
        
        # you can also use LinearSdirk
        # type help(LinearSdirkScheme) for a detailed help
        # the first argument is the order, the second argument the number of extra-stages
        ex_scheme = LinearSdirkScheme(4, 1)
        
        # and solve the ode with LinearSdirk
        Yf = SolveOde(0.0, 2.0, 20, Y0, ex_scheme, ex_ode);
        
        # a last class has been implemented: LinearRkScheme
        # these schemes are explicit Runge-Kutta with optimized coefficients
        # to improve the CFL for wave equation discretized with HDG (Hybridizable Discontinuous Galerkin)
        # the first argument is the order, the second argument the number of extra-stages
        ex_scheme = LinearRkScheme(4, 1)
        
        # and solve the ode with an explicit scheme
        Yf = SolveOde(0.0, 2.0, 20, Y0, ex_scheme, ex_ode);