Transformation d'une serie temporelle

1. Transformation d'une série temporelle en utilisant la procedure Expand. Soit une série de test

    
      1990  6 129.9 
      1990  7 130.4 
      1990  8 131.6 
      1990  9 132.7 
      1990 10 133.5 
      1990 11 133.8 
      1990 12 133.8 
      1991  1 134.6 
      1991  2 134.8 
      1991  3 135.0 
      1991  4 135.2 
      1991  5 135.6 
      1991  6 136.0 
      1991  7 136.2 
      ;
   

   Calculer et tracer $BX(t)$, $B^2X(t)$, $FX(t)$, $F^2X(t)$, $\mbox{CMA}(3)X(t)$(Moyenne mobile centrée), $\log X(t)$.

2. Simulation d'une série temporelle deterministe
   1. Créer une série temporelle hypothétique définit pour $t\in \{1,2,\cdots,12*10\}$.
      
      $$\displaystyle x_t = \sin\left (\frac{2\pi}{1\times 12}t\righ... ...displaystyle y_t = x_t+5\sin\left (\frac{2\pi}{3.3}t\right )$$
      
      

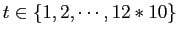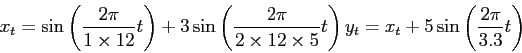
   2. tracer ces deux series de facon superposée.