Charles Deledalle's Résumé

Experience
- Research Scientist / Engineer -- Machine Learning
Research and Development Department, Brain Corporation, California, USA,
Since March 2020.
- Visiting professor at UCSD
ECE department (UC San Diego, California, USA),
From January, 2017 to Decembre 2019


- CNRS Research associate
IMB (Université Bordeaux, France),
From November, 2012 to Decembre 2018

- Postdoc position on risk estimation for inverse problems
CEREMADE laboratory at Université Paris Dauphine (Paris, France),
From November, 2011 to October 2012

- Sessional lecturer
Université Pierre et Marie Currie (Paris 6, France),
From October, 2008 to June, 2011

- Invited researcher on speckle denoising for high-resolution F-SAR images
German aerospace center - DLR (Oberpfaffenhofen, Germany),
From April, 2011 to May, 2011

- M.Sc Research internship
LTCI, département TSI (Telecom ParisTech, Paris, France),
Synthetic Aperture Radar denoising
From April, 2008 to September, 2008

- Research on text-independent Speaker Verification
EPITA Research and Development Laboratory (EPITA, Kremlin Bicêtre, France)
From January, 2005 to September, 2008
- Search Engine Opitimisation
AddedLifeValue (Düsseldorf, Deutschland)
Study of the Google policy, setting of Divorce.fr in 2nd rank in Google.fr
From April, 2007 to August, 2007
- Associated member with M2pi Ltd.
M2pi Ltd. (Paris, France)
Software development in C/C++, Java/JSP and Ruby on Rails
From 2002 to 2006
Education

- Phd student in signal and image processing
LTCI, département TSI (Telecom ParisTech, Paris, France),
Régularisation, extraction d'informations et interprétation en imagerie SAR multi-modalités
with Florence Tupin (Supervisor), Isabelle Bloch (Co-supervisor) and Loïc Denis (Collaborator).
From Octobre, 1st 2008 to Septembre, 30th 2011

- Master of Science degree in Sciences and Technologies
Université Pierre et Marie Currie (Paris 6, France)
Specialize in Artificial Intelligence and Decision Theory
Major in Information retrieval and Multimedia
Graduated with first class honours
From September, 2007 to Septembre, 2008

- Engineering degree of computer science
Ecole Pour l'Informatique et les Techniques Avancées (EPITA, Kremlin Bicêtre, France)
Major in Scientific calculus and Image processing
Graduated with first class honours
From September, 2005 to Septembre, 2008

- Exchange student at Utrecht university
Utrecht University (Utrecht, Netherlands)
Depatment of Computer Science
Section of Agent Technologies
From September, 2006 to January, 2007
- Post-secondary preparatory school in mathematics
Ecole Pour l'Informatique et les Techniques Avancées (EPITA, Kremlin Bicêtre, France)
From September, 2003 to June, 2005
- Baccalauréat scientifique
Lycée Notre-Dame (France)
Major in mathematics
Graduated with honours
June, 2003
PhD

- Subject:
Image denoising beyond additive Gaussian noise
Patch-based estimators and their application to SAR imagery
- Done at the signal and image processing department of the LTCI laboratory of Telecom ParisTech
with Florence Tupin (Supervisor) and Loïc Denis (Co-supervisor).
From October 1st, 2008 to September 30th, 2011
-
Defended on November 15, 2011. Jury members:
Jose Bioucas Dias Instituto de Telecomunicações Rapporteur Jean-François Giovannelli Univiversité Bordeaux 1 Examinateur Laure Blanc-Féraud CNRS -- Sophia Antipolis Présidente Jean-Michel Morel ENS Cachan Rapporteur Philippe Réfrégier Ecole centrale de Marseille Rapporteur Andreas Reigber German Aerospace Center, DLR Examinateur
Recent publications
Some of the publications below have appeared in an IEEE journal, Springer journal, Elsevier journal or conference record. By allowing you to download them, I am required to post the following copyright reminder: "This material is presented to ensure timely dissemination of scholarly and technical work. Copyright and all rights therein are retained by authors or by other copyright holders. All persons copying this information are expected to adhere to the terms and constraints invoked by each author's copyright. In most cases, these works may not be reposted without the explicit permission of the copyright holder."

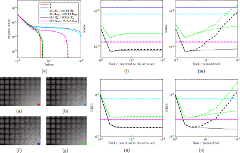
Shibin Parameswaran, Charles-Alban Deledalle, Loïc Denis, Truong Q. Nguyen IEEE Transactions on Image Processing, vol. 28, no. 2, pp. 687-698, 2019 (IEEE Xplore, recommended pdf, HAL, ArXiv) Presented at 5G and Beyond forum, May 2018, La Jolla, CA, USA (poster) Image restoration methods aim to recover the underlying clean image from corrupted observations. The Expected Patch Log-likelihood (EPLL) algorithm is a powerful image restoration method that uses a Gaussian mixture model (GMM) prior on the patches of natural images. Although it is very effective for restoring images, its high runtime complexity makes EPLL ill-suited for most practical applications. In this paper, we propose three approximations to the original EPLL algorithm. The resulting algorithm, which we call the fast-EPLL (FEPLL), attains a dramatic speed-up of two orders of magnitude over EPLL while incurring a negligible drop in the restored image quality (less than 0.5 dB). We demonstrate the efficacy and versatility of our algorithm on a number of inverse problems such as denoising, deblurring, super-resolution, inpainting and devignetting. To the best of our knowledge, FEPLL is the first algorithm that can competitively restore a 512x512 pixel image in under 0.5s for all the degradations mentioned above without specialized code optimizations such as CPU parallelization or GPU implementation. |
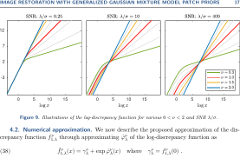
Charles-Alban Deledalle, Shibin Parameswaran, Truong Q. Nguyen SIAM Journal on Imaging Sciences, vol. 11, no. 4, pp. 2568-2609, 2018 (epubs SIAM, HAL, ArXiv) Presented at LIRMM Seminar, Jan 2019, Montpellier, France (slides) Patch priors have become an important component of image restoration. A powerful approach in this category of restoration algorithms is the popular Expected Patch Log-likelihood (EPLL) algorithm. EPLL uses a Gaussian mixture model (GMM) prior learned on clean image patches as a way to regularize degraded patches. In this paper, we show that a generalized Gaussian mixture model (GGMM) captures the underlying distribution of patches better than a GMM. Even though GGMM is a powerful prior to combine with EPLL, the non-Gaussianity of its components presents major challenges to be applied to a computationally intensive process of image restoration. Specifically, each patch has to undergo a patch classification step and a shrinkage step. These two steps can be efficiently solved with a GMM prior but are computationally impractical when using a GGMM prior. In this paper, we provide approximations and computational recipes for fast evaluation of these two steps, so that EPLL can embed a GGMM prior on an image with more than tens of thousands of patches. Our main contribution is to analyze the accuracy of our approximations based on thorough theoretical analysis. Our evaluations indicate that the GGMM prior is consistently a better fit for modeling image patch distribution and performs better on average in image denoising task. |
Jérémie Bigot, Charles Deledalle, Delphine Féral Journal of Machine Learning Research, vol. 18, no. 137, pp. 1-50, 2017 (JMLR, ArXiv) Presented at ISNPS'2018, June, Salerno, Italy (slides) We consider the problem of estimating a low-rank signal matrix from noisy measurements under the assumption that the distribution of the data matrix belongs to an exponential family. In this setting, we derive generalized Stein's unbiased risk estimation (SURE) formulas that hold for any spectral estimators which shrink or threshold the singular values of the data matrix. This leads to new data-driven shrinkage rules, whose optimality is discussed using tools from random matrix theory and through numerical experiments. Our approach is compared to recent results on asymptotically optimal shrinking rules for Gaussian noise. It also leads to new procedures for singular values shrinkage in matrix denoising for Poisson-distributed or Gamma-distributed measurements. |
[All] [Scholar Google]
Awards

|
UCSD ECE Best Lecturer Award. For my graduate classes on Machine Learning and Image Processing. |

|
IEEE GRSS 2016 Transaction Prize Paper Award for the paper "NL-SAR: a unified Non-Local framework for resolution-preserving (Pol)(In)SAR denoising", Authors: Charles-Alban Deledalle, Loïc Denis, Florence Tupin, Andreas Reigber and Marc Jäger. |

|
2013 CNRS Bonus for Scientific Excellence for my works on "Inference and consideration of complex and varied natural image models for restoration purposes" |

|
2011 PhD award in Signal, Image and Vision. Club EEA / GdR ISIS / GRETSI for the thesis "Image denoising beyond additive Gaussian noise - Patch-based estimators and their application to SAR imagery" |

|
Best student paper award IEEE ICIP 2010 for the paper "Poisson NL Means: Unsupervised Non Local Means for Poison Noise", Authors: Charles-Alban Deledalle, Loïc Denis and Florence Tupin. |
Seminars, invited speakers and workshops:
| Oct. 2019 | ECE Seminar, SDSU, California, 2019 | Host: C. Mi |
| Jan. 2019 | LIRMM Seminar, Université de Montpellier, France, 2019 | Host: N. Faraj |
| June 2017 | TII Seminar, Télécom ParisTech, France, 2017 | Host: F. Tupin |
| Feb. 2017 | UCSD ECE Seminar, San Diego, USA, 2017 | Host: T. Nguyen |
| Oct. 2016 | SPOC Seminar, Université de Bourgogne, Dijon, France, 2016 | Host: S. Vaiter |
| May 2016 | SIAM Conf. on Imaging Science, Albuquerque, USA | Host: C. Schönlieb & A. Langer |
| May 2016 | SAR Seminar, Télécom ParisTech, France, 2016 | Host: F. Tupin |
| July 2015 | Full-day tutorial at IGARSS, Milano, Italy, 2015 | |
| Aug. 2014 | Seminar SCIL, Université de Sherbrooke, Canada | Host: M. Descoteaux |
| July 2014 | Summerschool TUM/DLR, Ftan, Switzerland | Host: R. Bamler |
| May 2014 | SIAM Conference on Imaging Science, Hong-Kong | Host: R. Willett & R. Giryes |
| April 2014 | Seminar Cluster CPU/LaBEX COTE, Bordeeaux, France | Host: A.-L. Bué |
| March 2014 | Seminaires Patchs, Telecom ParisTech, France | Host: A. Almansa |
| March 2014 | Journée SIERRA, Saint-Etienne, France | Host: J. Debayle |
| Feb. 2014 | Salon Aquitec - Stand CNRS Parc des expositions de Bordeaux Lac | |
| Jan. 2014 | Seminar CESBIO, Toulouse, France | Host: Y. Kerr |
| Nov. 2013 | Journées Télédétection PEPS WAVE, Bordeaux, France | Host: L. Bombrun |
| Oct. 2013 | Atelier ForM@ter MDIS, Autrans, France | Host: M.-P. Doin |
| Sept. 2013 | Conférence GRETSI, Session Plénière, Brest, France | Host: GRETSI |
| March 2013 | Groupe de Travail Image, Bordeaux, France | Host: P. Coupé |
| Fév. 2013 | Salon Aquitec - Stand CNRS Parc des expositions de Bordeaux Lac | |
| Fév. 2013 | Séminaire TSI Télécom ParisTech | Hôte : I. Bloch |
| Déc. 2012 | GdR ISIS "Modèles de textures" Télécom ParisTech | Hôtes : J-F. Aujol & Y. Gousseau |
| Oct. 2012 | Journée FRUMAM Univ Aix-Marseilles | Hôte : F-X. Dupé & C. Melot |
| Juil. 2012 | Workshop ANR NatImages Nice | Hôte : J. Bobin |
| Mars 2012 | Séminaire LATP Univ. Aix-Marseilles | Hôte : F-X. Dupé |
| Mars 2012 | Séminaire I3S Univ. Nice Sofia-Antipolis | Hôte : L. Blanc-Féraud |
| Fév. 2012 | Séminaire LAGIS École Centrale de Lille | Hôte : P. Chainais |
| Fév. 2012 | Séminaire IMB/LaBRI/IMS Univ. Bordeaux 1 | Hôte : C. Dossal |
| Juin 2011 | Séminaire GREYC ENSICAEN, Caen | Hôte : L. Condat |
| Mai 2011 | Congrès SMAI Guidel, Bretagne | Hôtes : J. Delon & C. Louchet |
| Sept. 2010 | Séminaire Observatoire de Lyon Univ. Lyon 1 | Hôte : E. Thiébaut |
| Mai 2010 | Séminaire IETR Univ. Rennes 1 | Hôte : E. Pottier |
Last modified: Tue Mar 10 03:48:09 Europe/Berlin 2020