ARIMA(1,1,1) : Test stationnarité (ADF) et Identification avec minic scan esacf

1. Stationnarité par les tests de Augumented Dicker-Fuller.
   1. Etudier avec la même méthode la série simulé par 3.2.4 (avec rannor(1))

       
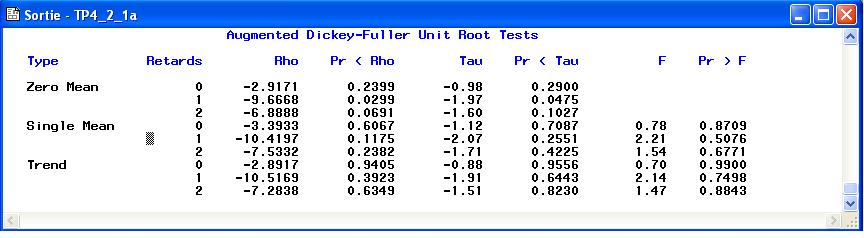
      title1 'Simulated ARIMA(1,1,1)';
      data a;
          u1=0; u2=0 ; a1 = 0;
          do i = -50 to 200;
             a = 0.2*rannor(1);
             u = (4.0/3)*u1 - (1.0/3)*u2 + a + (1.0/6)*a1;
             if i > 0 then output;         
          u2 = u1; u1 = u; a1 = a;
          end;
        run;
      

      Tester la staionnarité avec l'option stationarity=(DICKEY); Expliquer les resultats.

      Corrigé Tous les colonnes de Pr>F et Pr<Tau sont vraisemblable, donc on peut accepter hyppthèse M1 : (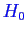 $H_0$ : le processus 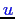$u$ possède une racine unitée, et la moyenne est zéro).

      

   2. Expliquer les resultats obtenus par la méthode

       
      identify var=u(1) nlag=12 minic scan esacf;run;+
      

      Corrigé la méthode minic propose BIC(2,0) mais la méthode scan considère que ARMA(1,1) est acceptable pour la processus u(1), parmi 7 modèles prosés on prévilège le plus simple.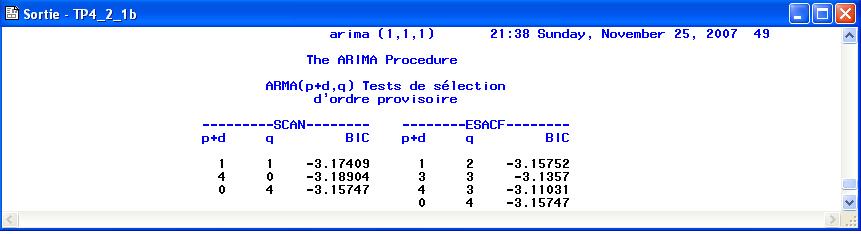

      
2. Les mêmes questions pour le processus simulés par 3.3.1.

   Corrigé

    
   title1 'Simulated ARIMA(1,1,1) avec derive';
   data a;
       u1=0; u2=0 ; a1 = 0;
       do i = -50 to 10000;
          a = 0.2*rannor(1);
          u = 0.1 + (4.0/3)*u1 - (1.0/3)*u2 + a + (1.0/6)*a1;
          if i > 0 then output;         u2 = u1; u1 = u; a1 = a;
       end;
     run;
   
   title1 'arima (1,1,1)';
   proc arima data=a;
      identify var=u stationarity=(DICKEY); run;
      /* on voit que il y a une racine unite le M3 est vraisemblable mais le modele M2
      n est pas vraisemblable, cad le processus u possede une racine, et il a une derive.
      avec une constante pour la difference premiere. Mais on ne peut pas accepter hypothese
      selon la quelle u possede qu une constante simple dans son modele.
      */
      identify var=u(1) minic scan esacf; run;
      /* avec un nombre de tirage 10000, on trouve un resultat minic BIC(1,1) */
      estimate p=1 q =1; run;
      /* avec ce modele, on voit que la residu est bruit blanc */
   quit;