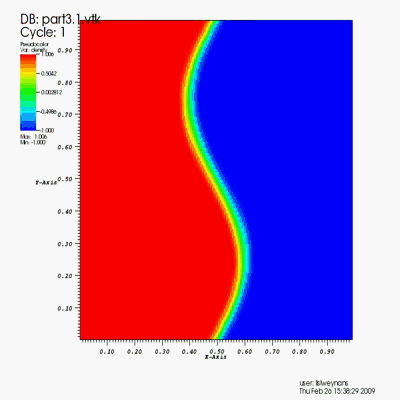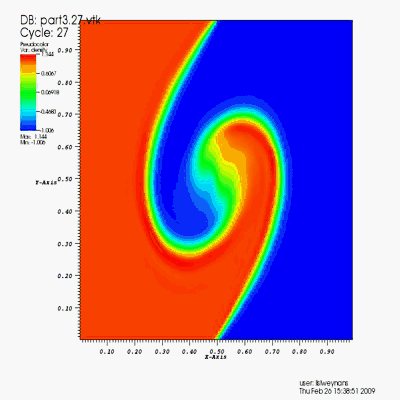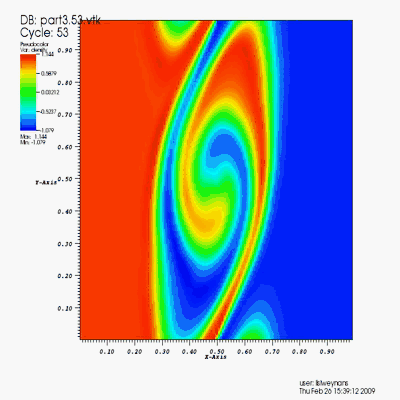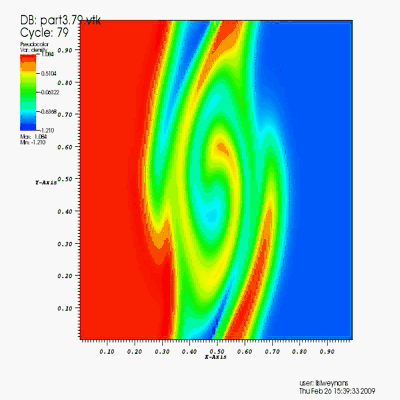
High Reynolds flows and their analysis
Participants: Charles-Henri Bruneau, Angelo Iollo, Iraj Mortazavi, Michel Bergmann, Lisl Weynans.
It is very exciting to model complex phenomena for high
Reynolds flows and to develop methods to compute the
corresponding approximate solutions, however a
well-understanding of the phenomena is necessary.
Classical graphic tools give us the possibility to
visualize some aspects of the solution at a given time and
to even see in some way their evolution. Nevertheless in
many situations it is not sufficient to understand the
mechanisms that create such a behavior or to find the real
properties of the flow. It is then necessary to carefully
analyze the flow, for instance the vortex dynamics or to
identify the coherent structures to better understand
their impact on the whole flow behavior. The various
numerical methods used or developed to approximate the
flows depend on the studied phenomenon. Our goal is to
compute the most reliable method for each situation.
The first method, which is affordable in 2D, consists in a
directly solving of the genuine Navier-Stokes equations in
primitive variables (velocity-pressure) on Cartesian
domains. The bodies, around which the flow has to be
computed are modeled using the penalization method (also
named Brinkman-Navier-Stokes equations). This is an
immersed boundary method in which the bodies are
considered as porous media with a very small intrinsic
permeability. This method is very easy to handle as it
consists only in adding a mass term U=K in the momentum
equations. The boundary conditions imposed on artificial
boundaries of the computational domains avoid any
reflections when vortices cross the boundary. To make the
approximation efficient enough in terms of CPU time, a
multi-grid solver with a cell by cell Gauss-Seidel
smoother is used.
The second type of methods is the vortex method. It is a
Lagrangian technique that has been proposed as an
alternative to more conventional grid-based methods. Its
main feature is that the inertial nonlinear term in the
flow equations is implicitly accounted for by the
transport of particles. The method thus avoids to a large
extent the classical stability/accuracy dilemma of
finite-difference or finite-volume methods. This has been
demonstrated in the context of computations for high
Reynolds number laminar flows and for turbulent flows at
moderate Reynolds numbers. This method has recently
enabled us to obtain new results concerning the
three-dimensional dynamics of cylinder wakes.
The third method is to develop reduced order models (ROM)
based on a Proper Orthogonal Decomposition (POD). The POD
consists in approximating a given flow field U(x; t) with
a decomposition where the basis functions are empirical in
the sense that they derive from an existing data base
given for instance by one of the methods above. Then the
approximation of Navier-Stokes equations for instance is
reduced to solving a low-order dynamical system that is
very cheap in terms of CPU time. Nevertheless the ROM can
only restitute what is contained in the basis. Our
challenge is to extend its application in order to make it
an actual prediction tool.
The fourth method is a finite volume method on cartesian
grids to simulate compressible Euler or Navier-Stokes
Flows in complex domains. An immersed boundary-like
technique is developed to take into account boundary
conditions around the obstacles with order two accuracy.
Exemples: Turbulence simulations | POD simulations | Aeronautic
simulations | Bio-locomotion
simulations | Stability
analysis | Compressible
flows

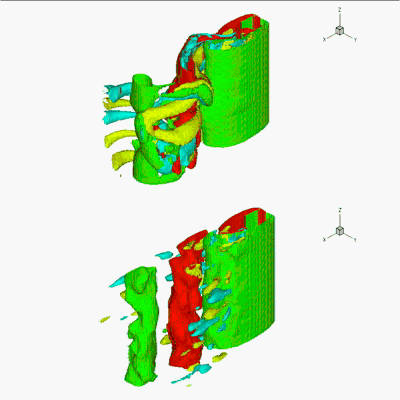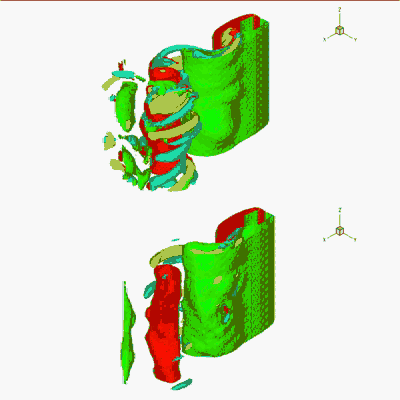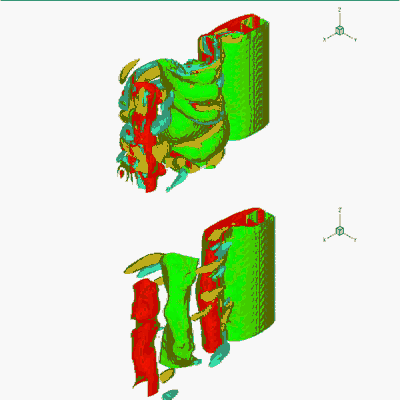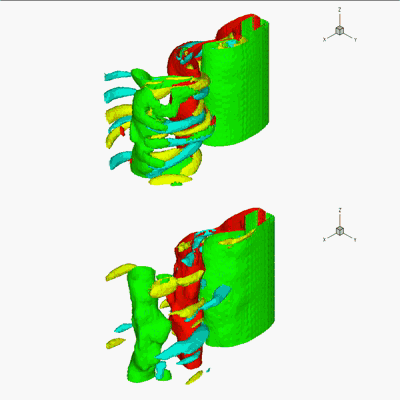
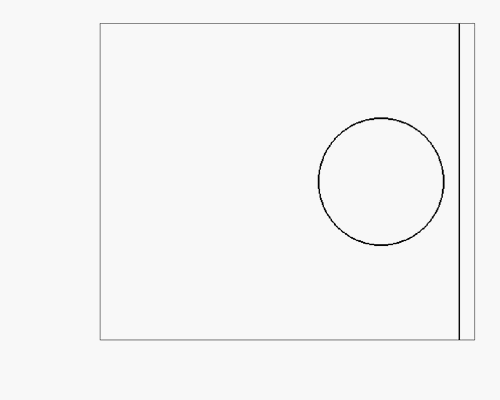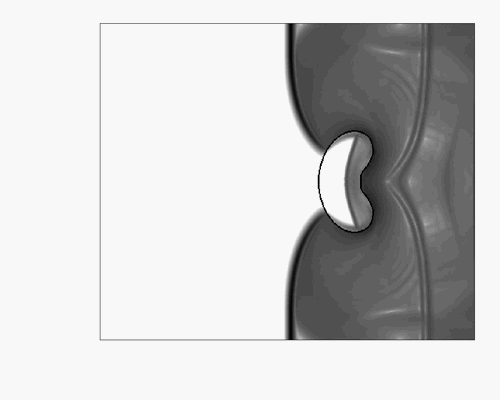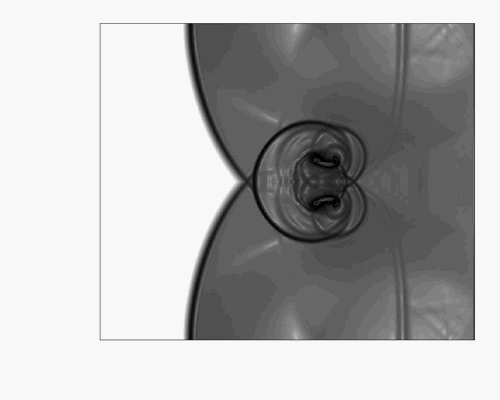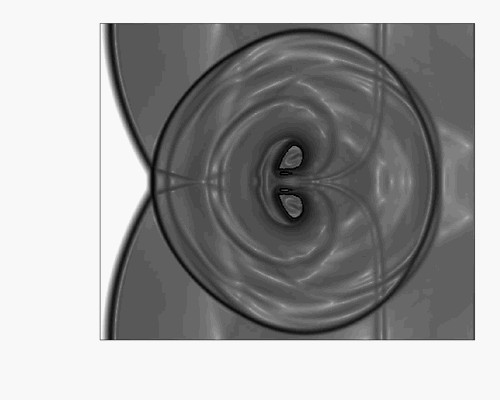
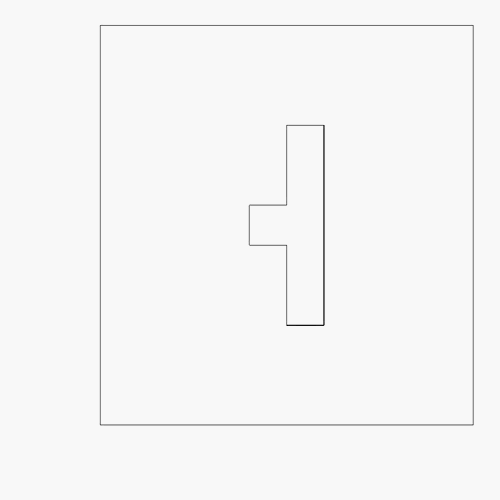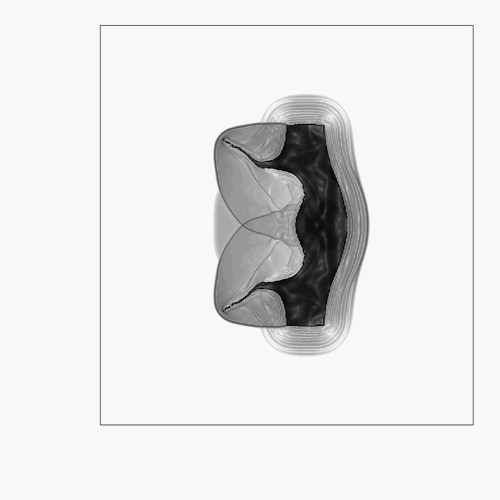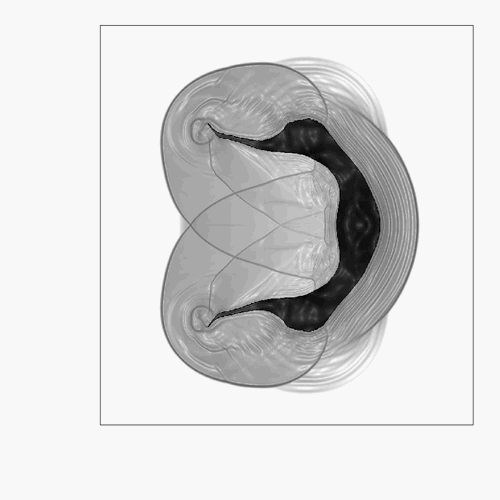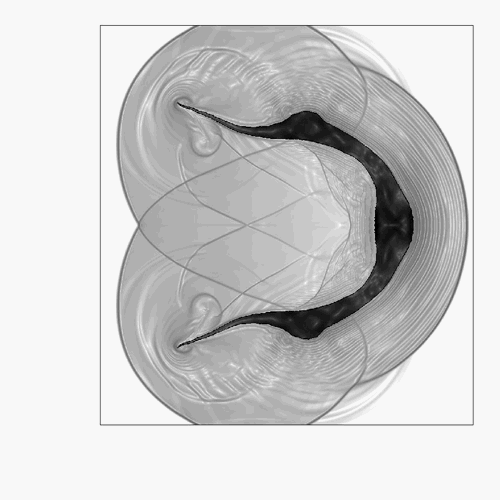
Turbulence simulation (Re=100 000).
The turbulence is generated by cylinders.
Numerical method: DNS (V-cycles multigrid method) + penalization.

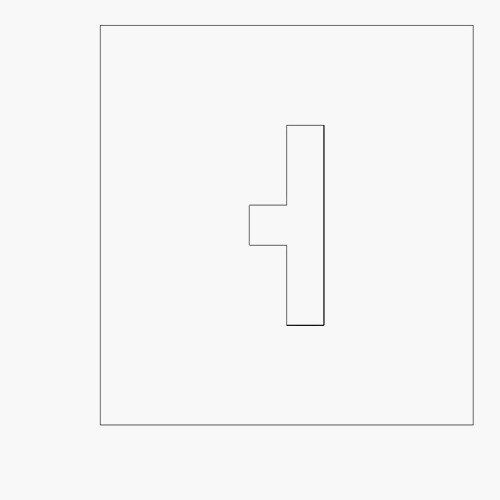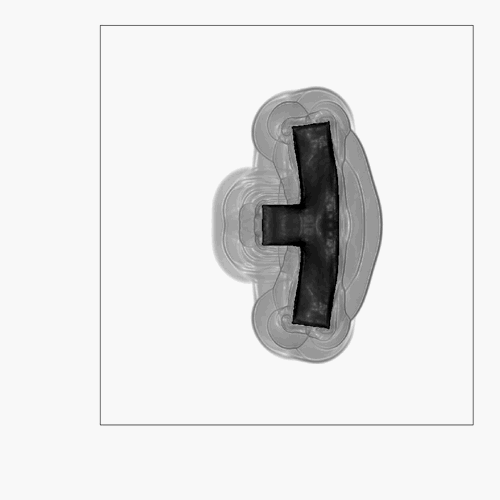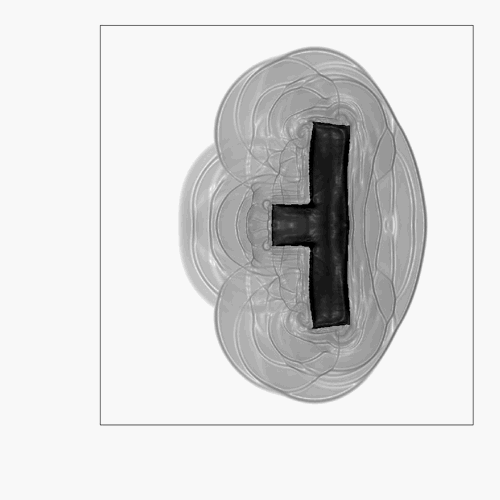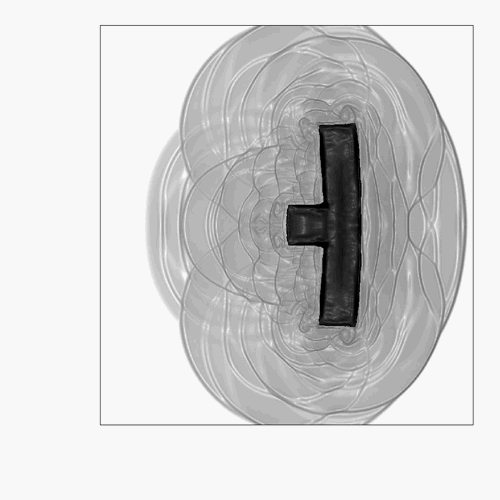
Windmill turbulence simulation (Re=1 000 000).
Numerical method: DNS + penalization + level set.
Comparison between DNS (top) and POD ROM (60 modes, bottom).
AERO solver was developped by B. Koobus and A. Dervieux (INRIA)
POD ROM = Reduced Order Model based on Proper Orthogonal Decompistion.

Numerical method: vortex method + penalization + level set.