Presentation of the INRIA MC2 team project

The aim of this project is to develop modelling tools for problems involving fluid mechanics in order to explain, to control, to simulate and possibly to predict some complex phenomena coming from physics, chemistry, biology or scientific engineering. The complexity may consist of the model itself, of the coupling phenomena, of the geometry or of non-standard applications. The challenges of the scientific team are to develop stable models and efficient adapted numerical methods in order to recover the main physical features of the considered phenomena. The models will be implemented into numerical codes for practical and industrial applications.

We are interested in both high and low Reynolds number flows, interface and control problems in physics and biology.

Our scientific approach may be described as follows. We first determine some reliable models and then we perform a mathematical analysis (including stability). We then develop the efficient numerical methods, which are implemented for specific applications.





FLUID MECHANICS

Interface problems and complex fluids


Collision.

Newtonian fluid flows simulations and their analysis



 
Turbulence. 

Flow control and shape optimization


Fish like swimming.

This concerns microfluidics, complex fluids (bifluid flows, miscible fluids). The challenges are to obtain reliable models that can be used by our partner Rhodia (for microfluidics)
 We want to develop numerical methods in order to address the complexity of high Reynolds flows. The challenges are to find scale factors for turbulent flow cascades, and to develop modern and reliable methods for computing flows in aeronautics in a realistic configuration.
 The challenges are the drag reduction of a ground vehicle, the reduction of turbomachinery noise emissions or the increase of lift-to-drag ratio in airplanes, the control of flow instabilities and the detection of embedded defects in materials.




MEDICINE

Image-based prediction of tumor growth







Theory and modeling for cancer biology

 

Biophysical modeling of anti-cancerous therapies



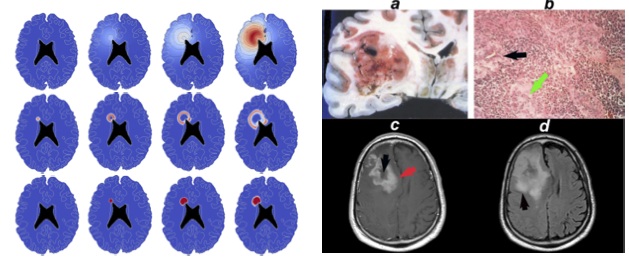
Based on clinical images of a given patient (CT scan or MRI), we develop simple spatial models of tumor growth (nonlinear partial differential equations) and numerical methods for resolution of the inverse problem (parameter estimation) and try to predict the future fate of a given tumor (growth, stabilization or regression) in order to give improve prognosis and therapeutic decision
 To gain biological understanding of complex phenomena, we develop theoretical mathematical models for various processes of cancer biology such as avascular and vascular tumor growth but also development of a cancer disease at the organism level, integrating the metastatic process, which represents the major cause of death in a cancer disease (90%). These models yield insights about various topics including anti-angiogenic therapies, metastatic dormancy or post-surgery metastatic acceleration
 Transdisciplinary project developing new mathematical models, numerical tools and experimental protocols to provide complete understanding of cell electropermeabilization from the cell to the tissue scale


The challenge is to produce patient-specific simulations starting from medical imaging for growth of metastasis to the lung of a distant tumor.


Members

Research Scientist

Faculty Member

  • Afaf Bouharguane
  • Charles-Henri Bruneau [ Pr, Université Bordeaux 1, HdR ]
  • Thierry Colin [ Team Leader, Pr, Institut Universitaire de France, HdR ]
  • Mathieu Colin [ MC, Université Bordeaux 1 ]
  • Angelo Iollo [ Pr, Université Bordeaux 1, HdR ]
  • Iraj Mortazavi [ MC, Université Bordeaux 1, HdR ]
  • Kevin Santugini [ MC, Université Bordeaux 1 ]
  • Lisl Weynans [ MC, Université Bordeaux 1 ]

PhD Student

  • Florian Bernard
  • François Cornélis
  • Alexia De Brauer 
  • Julien Jouganous
  • Manuel Latige
  • Guillaume Lefèvre
  • Michael Leguebe
  • Vivien Pianet
  • Hervé Ung
  • Xin Jin

Post-Doctoral Fellow

  • Julie Joie
  • Yong-Liang Xiong

Administrative Assistant

  • Anne-Laure Gautier

Associate members

  • Patrick Fischer [ MC, Université Bordeaux 1 ]
  • Khodor Khadra [ Visiting technical staff ]
  • Guy Métivier [ PR, Institut Universitaire de France, HdR ]
  • Mazen Saad [ PR, École Centrale Nantes, HdR ]

Invited Member

  • Patricio Andrés Cumsille Atala