Control and optimization

Participants: Charles-Henri Bruneau, Angelo Iollo, Iraj Mortazavi, Michel Bergmann.

Flow simulations, optimal design and flow control have been developed these last years in order to solve real industrial problems : vortex trapping cavities with CIRA (Centro Italiano Ricerche Aerospaziali), reduction of vortex induced vibrations on deep sea riser pipes with IFP (Institut Français du Pétrole), drag reduction of a ground vehicle with Renault or in-flight icing with Bombardier and Pratt-Wittney are some examples of possible applications of these researches. Presently the recent creation of the competitiveness cluster on aeronautics, space and embedded systems (AESE) based also in Aquitaine provides the ideal environment to extend our applied researches to the local industrial context. There are two main streams: the first need is to produce direct numerical simulations, the second one is to establish reliable optimization procedures. In the next subsections we will detail the tools we will base our work on, they can be divided into three points: to find the appropriate devices or actions to control the flow; to determine an effective system identification technique based on the trace of the solution on the boundary; to apply shape optimization and system identification tools to the solution of inverse problems found in object imaging and turbomachinery.

Control of flows
There are mainly two approaches: passive (using passive devices on some specific parts that modify the shear forces) or active (adding locally some energy to change the flow) control. The passive control consists mainly in adding geometrical devices to modify the flow. One idea is to put a porous material between some parts of an obstacle and the flow in order to modify the shear forces in the boundary layer. This approach may pose remarkable difficulties in terms of numerical simulation since it would be necessary, a priori, to solve two models: one for the fluid, one for the porous medium. However, by using the penalization method it becomes a feasible task. This approach has been now used in several contexts and in particular in the frame of a collaboration with IFP to reduce vortex induced vibrations.
Another technique we are interested in is to inject minimal amounts of polymers into hydrodynamic flows in order to stabilize the mechanisms which enhance hydrodynamic drag.
The active approach is addressed to conceive, implement and test automatic flow control and optimization aiming mainly at two applications : the control of unsteadiness and the control and optimization of coupled systems. Implementation of such ideas relies on several tools. The common challenges are infinite dimensional systems, Dirichlet boundary control, nonlinear tracking control, nonlinear partial state observation. The bottom-line to obtain industrially relevant control devices is the energy budget. The energy required by the actuators should be less than the energy savings resulting from the control application. In this sense our research team has gained a certain experience in testing several control strategies with a doctoral thesis (E. Creusé) devoted to increasing the lift on a dihedral plane. Indeed the extension of these techniques to real world problems may reveal itself very delicate and special care will be devoted to implement numerical methods which permit on-line computing of actual practical applications. For instance the method can be successful to reduce the drag forces around a ground vehicle and a coupling with passive control is under consideration to improve the efficiency of each control strategy. 

System identification
We remark that the problem of deriving an accurate estimation of the velocity field in an unsteady complex flow, starting from a limited number of measurements, is of great importance in many engineering applications. For instance, in the design of a feedback control, a knowledge of the velocity field is a fundamental element in deciding the appropriate actuator reaction to different flow conditions. In other applications it may be necessary or advisable to monitor the flow conditions in regions of space which are difficult to access or where probes cannot be fitted without causing interference problems.
The idea is to exploit ideas similar to those at the basis of the Kalman filter. The starting point is again a Galerkin representation of the velocity field in terms of empirical eigenfunctions. For a given flow, the POD modes can be computed once and for all based on Direct Numerical Simulation (DNS) or on highly resolved experimental velocity fields, such as those obtained by particle image velocimetry. An instantaneous velocity field can thus be reconstructed by estimating the coefficients ai(t) of its Galerkin representation. One simple approach to estimate the POD coefficients is to approximate the flow measurements in a least square sense.
A similar procedure is also used in the estimation based on gappy POD. However, these approaches encounter difficulties in giving accurate estimations when three-dimensional flows with complicated unsteady patterns are considered, or when a very limited number of sensors is available. Under these conditions, for instance, the least squares approach cited above (LSQ) rapidly becomes ill-conditioned. This simply reflects the fact that more and more different flow configurations correspond to the same set of measurements.
Our challenge is to propose an approach that combines a linear estimation of the coefficients ai(t) with an appropriate non-linear low-dimensional flow model, that can be readily implemented for real time applications.

Shape optimization and system identification tools applied to inverse problems found in object imaging and turbomachinery
We will consider two different objectives. The first is strictly linked to the level set methods that are developed for microfluidics. The main idea is to combine different technologies that are developed with our team: penalization methods, level sets, an optimization method that regardless of the model equation will be able to solve inverse or optimization problems in 2D or 3D. For this we have started a project that is detailed in the research program.
As for shape optimization in aeronautics, the aeroacoustic optimization problem of propeller blades is addressed by means of an inverse problem and its adjoint equations. This problem is divided into three subtasks:
i) formulation of an inverse problem for the design of propeller blades and determination of the design parameters
ii) derivation of an aeroacoustic model able to predict noise levels once the blade geometry and the flow field are given
iii) development of an optimization procedure in order to minimize the noise emission by controlling the design parameters.
The main challenge in this field is to move from simplified models to actual 3D model. The spirit is to complete the design performed with a simplified tool with a fully three dimensional inverse problem where the load distribution as well as the geometry of the leading edge are those provided by the meridional plane analysis. A 3D code will be based on the compressible Euler equations and an immersed boundary technique over a cartesian mesh. The code will be implicit and parallel, in the same spirit as what was done for the meridional plane. Further development include the extension of the 3D immersed boundary approach to time-dependent phenomena. This step will allow the designer to take into account noise sources that are typical of internal flows. The task will consist in including time dependent forcing on the inlet and/or outlet boundary under the form of Fourier modes and in computing the linearized response of the system. The optimization will then be based on a direct approach, i.e., an approach where the control is the geometry of the boundary. The computation of the gradient is performed by an adjoint method, which will be a simple "byproduct" of the implicit solver. The load distribution as well as the leading edge geometry obtained by the meridional plane approach will be considered as constraints of the optimization, by projection of the gradient on the constraint tangent plane. These challenges will be undertaken in collaboration with Politecnico di Torino and EC Lyon.

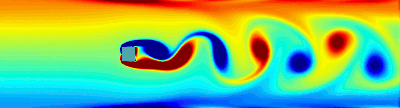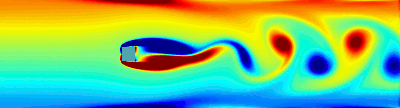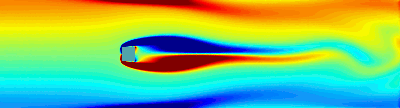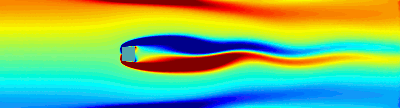
Examples: Drag minimization |  Lift maximization |  Thrust generation |  Shape optimization