Estimation des parametres par SAS

1. Ecrire le modèle MA(2) 1.4.2 sous forme canonique (telle que les racines du polynôme 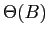$\Theta(B)$ ont modules strictement superieures à 1. Estimer les paramètres avec la méthode estimate du processus arima

2. Estimer les paramètres du modèle 2.1.3.

3. Estimer les paramètres du modèle 2.1.6.
4. . On considère maintenant le processus ARIMA(1,1,1) suivant
   
   $$(1-\frac23B)(1-B) X_t = \varepsilon _t + \frac56 \varepsilon _{t-1}   \mbox{o\\lq u}  \varepsilon \sim N(0,0.2^2)$$
   
   
   1. Est-ce que le modèle est sous la forme canonique ?

   2. Simuler ce processus.
   3. On suppose que les ordre (p,d,q) = (1,1,1) sont connus, identifier et estimer les parametres de ce processus. Expliquer chacun des resultats.