LICENCE
    Polycopiés de Licence. Les fichiers sont au format pdf ou PostScript compressé par gzip.


Intégration : Cours d'intégration, 1992 (111 pages, fichier pdf 1414461octets; fichier Postscript compressé par gzip 348914 octets disponible ici). Contenu:
  1. Espaces et fonctions mesurables, mesures
    1. Tribus
    2. Mesurabilité
      1. Espaces et fonctions mesurables
      2. Fonctions étagées
    3. Mesures
      1. Définition et propriétés générales, exemples
      2. Mesures positives, ensembles négligeables, complétion
      3. Mesures complexes, variation totale, absolue continuité
      4. Convergence en mesure
  2. Intégration abstraite
    1. Intégration des fonctions mesurables positives
      1. Intégration des fonctions étagées
      2. Intégration des fonctions mesurables positives
    2. Intégration des fonctions réelles et complexes
    3. Intégrales dépendant d'un paramètre
  3. Espaces Lp
    1. Espaces L1
    2. Inégalités de convexité
    3. Espaces Lp
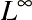
    4. Espaces L-infini
    5. Théorème de Radon-Nikodym, dualité entre espaces Lp
      1. Théorème de Radon-Nikodym
      2. Dualité
      3. Convergence faible
  4. Mesures de Radon et mesures de Borel
    1. Espaces topologiques localement compacts
    2. Mesures de Borel et mesures de Radon sur un espace localement compact
    3. Le mesure de Lebesgue
    4. Fonctions continues et fonctions mesurables sur un espace localement compact
    5. Le Théorème de représentation de Riesz
  5. Produit de mesures
    1. Classes monotones
    2. Produits finis d'espaces mesurables
    3. Produits finis d'espaces mesurés
    4. Le Théorème de Fubini
    5. Complétion des espaces produits
  6. Changement de variables
    1. Image d'une mesure par une application mesurable
      1. Définition et propriétés générales
      2. Propriétés particulières à la mesure de Lebesgue
    2. Le Théorème de changement de variables
    3. Intégration en coordonnées polaires
      1. Mesure invariante sur la sphère unité
      2. Intégration en coordonnées polaires
    4. Mesure naturelle sur une sous-variété différentiable
      1. Cas de sous-variétés paramétrées
      2. Cas général
      3. Un théorème d'intégration par tranches
  7. Convolution
    1. Convolution des fonctions mesurables
      1. Définition et premières propriétés
      2. Convolution dans les espaces Lp
    2. Régularisation des fonctions mesurables
    3. Convolution des mesures boréliennes
      1. Cas des mesures positives
      2. Cas général
    4. Convolution d'une mesure et d'une fonction
  8. Transformation de Fourier
    1. Transformation de Fourier des fonctions intégrables
      1. Définition, exemples
      2. Propriétés fondamentales
      3. Procédés de sommation
      4. Le théorème classique de réciprocité
    2. La transformation de Fourier sur l'espace de Schwarz
    3. La transformation de Fourier-Plancherel
Topologie : Cours de topologie, 2000-01 (127 pages, fichier pdf 1261898 octets; fichier Postscript compressé par gzip 529043 octets disponible ici). Contenu:
  1. Les nombres réels
    1. Une construction des réels
    2. Suites de nombres réels
  2. Espaces métriques
    1. Vocabulaire topologique
    2. Espaces métriques, définition et premières propriétés
    3. Exemples
    4. Continuité dans les espaces topologiques et métriques
      1. Suites dans un espace métrique
      2. Fonctions continues
      3. Continuité uniforme, isométries
      4. Limites
    5. Espaces connexes
      1. Connexité
      2. Connexité par arcs
    6. Produit d’espaces topologiques et d’espaces métriques
    7. Espaces métriques complets
      1. Suites de Cauchy, espaces métriques complets
      2. Exemples d’espaces métriques complets
      3. Théorèmes de prolongement
      4. Complétion d’un espace métrique
      5. Théorèmes du point fixe
    8. Espaces compacts
      1. Espaces topologiques compacts
      2. Espaces métriques compacts
      3. Espaces localement compacts
      4. Compactification d’un espace
      5. Applications aux espaces de fonctions continues
  3. Espaces vectoriels normés
    1. Espaces normés et espaces de Banach
    2. Exemples
    3. Séries et familles sommables dans un espace normé
      1. Séries dans un espace normé
      2. Familles sommables et absolument sommables
      3. Séries commutativement convergentes
      4. Les espaces lpI(E) et c0(E)
    4. Espaces d’applications linéaires et multilinéaires continues
      1. Applications multilinéaires et linéaires continues
      2. Hyperplans fermés et formes linéaires continues
      3. Les Théorèmes de Banach et de Banach-Steinhaus
      4. Le Théorème de Hahn-Banach
      5. Dual d’un espace normé
      6. Duaux des espaces lpI(E) et c0(E)
    5. Espaces normés de dimension finie
      1. Structure des espaces normés de dimension finie
      2. Séries et familles sommables dans les espaces normés de dimension finie
  4. Espaces de Hilbert
    1. Formes hermitiennes
      1. Généralités
      2. Formes hermitiennes positives
      3. Exemples de formes hermitiennes
    2. Espaces préhilbertiens et Hilbertiens
    3. Exemples
    4. Projection sur un sous-ensemble convexe
      1. Projection sur un convexe séparé et complet
      2. Projection sur un cône convexe séparé et complet
      3. Projection sur un sous-espace vectoriel séparé et complet
      4. Dual d’un espace de Hilbert
      5. Sous-espaces orthogonaux supplémentaires
    5. Sommes hilbertiennes et bases hilbertiennes
      1. Somme hilbertienne externe d’espaces de Hilbert
      2. Somme hilbertienne de sous-espaces orthogonaux
      3. Familles orthonormales et bases hilbertiennes
      4. Orthonormalisation, existence des bases hilbertiennes
      5. Exemples de bases hilbertiennes
  5. Annexe :
    1. Axiome du choix et Lemme de Zorn
      1. L’axiome du choix
      2. Ensembles ordonnés : définitions de base
      3. Théorème de Zermelo et Lemme de Zorn
      4. Applications de l’axiome du choix aux espaces vectoriels
    2. Cardinalité des ensembles
      1. Cardinalité
      2. Ensembles dénombrables
      3. Cardinalité des ensembles infinis
Calcul Différentiel : Cours de calcul différentiel, 2000-01 (95 pages, fichier pdf 1029451 octets; fichier Postscript compressé par gzip 476481 octets disponible ici). Contenu:
  1. Calcul différentiel
    1. Fonctions différentiables
    2. Théorème des accroissements finis et applications
      1. Le Théorème des accroissements finis
      2. Applications du Théorème des accroissements finis
    3. Théorèmes d’inversion locale et des fonctions implicites
      1. Le Théorème d’inversion locale
      2. Le Théorème des fonctions implicites
    4. Différentielles d’ordre supérieurs
      1. Différentielles secondes
      2. Différentielles d’ordres supérieurs
    5. Formule de Taylor, développements limités
      1. La formule de Taylor
      2. Développements limités
      3. Opérateurs différentiels
    6. Applications
      1. Maxima et minima relatifs
      2. Conjugaison
      3. Sous-variétés différentiables, extrema liés
  2. Équations différentielles
    1. Généralités
      1. Définitions
      2. Bouts des solutions maximales
      3. Cylindres de sécurité
    2. Solutions approchées,Méthode d’Euler
    3. Théorèmes d’existence et d’unicité généraux
      1. Le cas de dimension finie : le Théorème de Cauchy-Peano-Arzela
      2. Le cas localement lipschitzien
        1. Lemmes de Gronwall, Lemme fondamental
        2. Le Théorème de Cauchy-Lipschitz
        3. Solutions globales
        4. Dépendance par rapport aux conditions initiales et à un paramètre
    4. Le Théorème des bouts
    5. Équations différentielles linéaires
      1. Définitions, existence et unicité des solutions
      2. Résolution des équations différentielles linéaires d’ordre 1
        1. Cas où E est de dimension finie
      3. Résolution des équations différentielles linéaires d’ordre n
        1. Équation différentielles linéaires scalaires d’ordre n
      4. Équations différentielles linéaires à coefficients constants
        1. Cas où E est de dimension finie
        2. Cas des équations d’ordre n
      5. Stabilité des solutions des équations différentielles linéaires
    6. Éléments d’études qualitatives en dimension 1