EDP et Physique mathématique

Responsable de l’équipe : Laurent Michel

Séminaire EDP et physique mathématique

Responsables du séminaire : Responsables : Jean-Baptiste Burie, Franck Sueur

GdT EDP et Théorie Spectrale

Responsable du groupe de travail : Jean-François Bony

Quelques anciens membres : Alain Bachelot (Pr honoraire), Gilles Carbou (Pr, Pau), Rémi Carles (DR CNRS, Rennes), Eric Darrigrand (MCF, Rennes1), Thierry Daudé (MCF, Cergy), Jérémy Faupin (Pr, Metz), Dietrich Häfner (Pr, Grenoble), Bernard Hanouzet (Pr honoraire), Yavar Kian (MCF, Aix-Marseille), Frédéric Naud (Pr, Sorbonne Université), Jean-Philippe Nicolas (Pr, Brest), Djomba Sambou (MCF, Orléans),Jérémie Szeftel (DR CNRS, Paris 6)

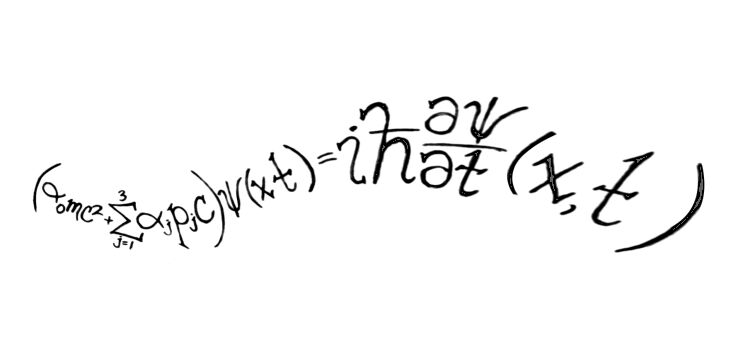
Les recherches de l’équipe portent sur de nombreux aspects de l’étude des EDP : lien avec l’analyse harmonique, analyse spectrale des EDP issues de la physique mathématique, équations nonlinéaires provenant en particulier de la mécanique des fluides, modèles cinétiques... Les applications concernent la mécanique des fluides (océanographie, interactions fluide-structures, fluides non newtoniens, plasmas, etc.), la mécanique quantique, la dynamique des populations, l’électromagnétisme, le ferromagnétisme, l’optique non linéaire, etc.

Thèmes

Analyse des EDP

Etude qualitative de solutions d’équations aux dérivées partielles linéaires et non linéaires :
– Description de singularités en mécanique des fluides
– Couches limites
– Singularités dans des domaines à coin
– Équations hyperboliques non linéaires 
– Existence et régularité de solutions 
– Existence et stabilité d’ondes solitaires 
– Comportement asymptotique des solutions
– Modèles cinétiques 
– Équation de Landau-Lifshitz-Gilbert 
– Équation de Hall-Magnétohydrodynamique 
– Équation de Maxwell-Bloch

Interaction fluide-structure :
– Dynamique de petits objets solides dans un fluide
– Interactions vagues structures
– Application à la cancerologie

Contrôle et Problèmes inverses :
– Contrôle pour les équations de Navier-Stokes,
– Equation des vagues
– Equation des ondes
– Inégalités de Carleman
– Problème inverse de diffusion, 
– Caractérisation électrique des cellules en biologie.

Physique Mathématique

Asymptotiques spectrales :
– Opérateurs non auto-adjoints 
– Limite semi-classique 
– Opérateurs de Schrödinger et de Dirac
– Répartition des valeurs propres et des résonances 
– Formules de trace 
– Fonction de décalage spectral 
– Opérateurs fibrés 
– Opérateurs magnétiques
– Perturbations singulières
– Problèmes de bords 
– Développements asymptotiques dans des domaines à bord singulier
– Métastabilité
– Processus de Markov
– Trous spectraux pour des processus stochastiques, applications aux modèles cinétiques
– Grandes déviations

Théorie de la diffusion classique et quantique :
–  Problèmes spectraux inverses
– Fonctions zêtas dynamiques
–  Equation des ondes
–  Systèmes dynamiques

Analyse spectrale et analyse microlocale de systèmes d’EDP :
– Systèmes hyperboliques
– Problème de transmission
– Opérateurs de Schrodinger matriciels et de Dirac

Analyse harmonique et EDP paraboliques : 
– Multiplicateurs spectraux 
– Transformées de Riesz sur les variétés 
– Contôle des équations d’évolution 
– Estimées des noyaux de la chaleur 
– Régularité maximale des équations non-autonomes
– Estimations de Strichartz
– Equations paraboliques en mécanique des fluides
– Problèmes à frontière libre
– Modèles de combustion

Modélisation et Analyse numérique

Dynamique de populations :
–  Modèles épidémiques 
–  Systèmes prédateurs proies
– Existence et stabilité d’ondes progressives
–  Évolution phénotypique 
–  Cancer et dynamique de population cellulaires 
–  Applications en biologie, écologie, médecine 

Modélisation, analyse et simulations en océanographie côtière :
– Modélisation
– Analyse théorique
– Analyse numérique

Modélisation, analyse et simulations en mécanique des fluides et physique des plasmas :
– Modèles fluides
– Modèles aux moments
– Modèles cinétiques pour les gaz complexes
– Perturbations dissipatives ou dispersives de systèmes hyperboliques,

Electromagnétisme :
– Ferromagnétisme 
– Effet Kerr 
– Interaction laser-plasma 
– Instabilités Brillouin 
– Supraconductivité

Rapport d’activité 2009-2014 : pdf