Quadrature rules in 1-D, 2-D and 3-D
For the integration on unit interval [0,1], Gauss quadrature rules are available, as well as Gauss-Lobatto and Gauss-Radau. The class Globatto contains integration points and weights, and the definition of Lagrange interpolation polynomials based on integration points. 2-D integration is possible on unit triangle and unit square, and 3-D integration can be achieved on unit tetrahedron, symmetric pyramid and unit hexahedron.
Basic use
// computation of integration rules on the unit interval
// basic Gaussian rules :
Vector<double> points, weights;
int r = 5;
// exact integration of Q_2r+1
ComputeGaussLegendre(points, weights, r);
// Gauss-Jacobi formulas for integration of \int f(x) (1-x)^alpha x^beta dx
double alpha = 2.0; beta = 1.0;
ComputeGaussJacobi(points, weights, r, alpha, beta);
// Gauss-Lobatto formulas :
// exact integration of Q_2r-1 (including extremities)
ComputeGaussLobatto(points, weights, r);
// Gauss-Jacobi-Lobatto :
ComputeGaussLobattoJacobi(points, weights, r, alpha, beta);
// for integration over the unit triangle (x, y >= 0, x+y <= 1)
// exact integration of P_p:
int p = 2*r;
VectR2 points2d;
// default rules are Dunavant rules
TriangleQuadrature::ConstructQuadrature(p, points2d, weights);
// several other rules are avaible :
// QUADRATURE_TENSOR : obtained with Duffy transformation and Gauss rules on the square
// QUADRATURE_MASS_LUMPED : mass-lumping rules (Mulder)
// QUADRATURE_QUASI_LUMPED : quasi mass-lumping rules (Imperiale)
TriangleQuadrature::ConstructQuadrature(p, points2d, weights, TriangleQuadrature::QUADRATURE_TENSOR);
// integration on unit square : basic tensorization
// 0 <= x, y <= 1
// exact integration of Q_p
QuadrangleQuadrature::ConstructQuadrature(p, points2d, weights);
// default rules are Gauss-Legendre rules, other rules :
// QUADRATURE_LOBATTO : Gauss-Lobatto rules
// QUADRATURE_GAUSS_SQUARED : change of variables to integrate exactly 1/sqrt(x)
// QUADRATURE_RADAU : Gauss-Radau rules (extremity 0 is a point of integration)
QuadrangleQuadrature::ConstructQuadrature(p, points2d, weights, Globatto<Real_wp>::QUADRATURE_LOBATTO);
// Jacobi-rules need to provide alpha and beta :
// QUADRATURE_JACOBI : Gauss-Jacobi rules
// QUADRATURE_RADAU_JACOBI : Gauss-Radau-Jacobi rules
// QUADRATURE_LOBATTO_JACOBI : Gauss-Lobatto-Jacobi rules
QuadrangleQuadrature::ConstructQuadrature(p, points2d, weights,
Globatto<Real_wp>::QUADRATURE_JACOBI, alpha, beta);
// integration over unit tetrahedron
// x, y, z >= 0 and x + y + z <= 1
VectR3 points3d;
// default rules provided in Solin book
TetrahedronQuadrature::ConstructQuadrature(p, points3d, weights);
// other rules :
// QUADRATURE_TENSOR : use of Duffy transformation and Gauss-rules on the cube
// QUADRATURE_MASS_LUMPED : mass-lumping rules (Mulder)
// QUADRATURE_QUASI_LUMPED : quasi mass-lumping rules (Imperiale)
TetrahedronQuadrature::ConstructQuadrature(p, points3d, weights,
TetrahedronQuadrature::QUADRATURE_TENSOR);
// integration over symmetric pyramid
// 0 <= z <= 1; -(1-z) <= x, y <= 1-z;
// points1d_z and weights1d_z are output arrays containing points and weights used along z-direction
Vector<double> points1d_z, weights1d_z;
PyramidQuadrature::ConstructQuadrature(r, points3d, weights, points1d_z, weights1d_z,
PyramidQuadrature::QUADRATURE_JACOBI2);
// QUADRATURE_JACOBI2 use Gauss-Jacobi rules with weight (1-z)^2
// QUADRATURE_JACOBI1 use Gauss-Jacobi rules with weight (1-z)
// QUADRATURE_GAUSS use Gauss-Legendre rules
// QUADRATURE_JACOBI2 should be the most accurate, other rules are interesting
// if there a singularity at the apex of the pyramid
// integration over unit cube is similar to the square :
HexahedronQuadrature::ConstructQuadrature(p, points3d, weights);
The class Globatto can also be used to compute Lagrangian interpolation functions based on quadrature points. The class SubdivGlobatto implements a regular subdivision of interval [0, 1], each sub-interval contains regular points or Gauss-Lobatto points.
Methods for Globatto :
| GetMemorySize | returns the memory used to store the object in bytes |
| GetOrder | returns the order of the integration rule |
| GetGeometryOrder | returns the order of the integration rule |
| GetNbPointsQuad | returns the number of quadrature points |
| ConstructQuadrature | computation of a quadrature rule |
| AffectPoints | changes the 1-D interpolation/quadrature points |
| AffectWeights | changes the 1-D interpolation/quadrature weights |
| Points | returns 1-D quadrature points |
| Weights | returns 1-D quadrature weights |
| EvaluatePhi | evaluates a single Lagrange interpolation polynomial |
| EvaluatePhiGrad | evaluates derivative of a Lagrange interpolation polynomial |
| GradPhi | returns derivatives of Lagrange interpolation polynomial at quadrature points |
| ComputeValuesPhiRef | computes Lagrange interpolation polynomials |
| ComputeGradPhi | computes derivatives of Lagrange interpolation polynomial at quadrature points |
Methods for SubdivGlobatto :
| Points | returns position of interpolation point i |
| Init | inits a regular subdivision of interval [0, 1] |
| InitPoints | inits a regular subdivision of interval [0, 1] and points for each subdivision |
| GetOrder | returns the number of interpolations points -1 |
| GetGeometryOrder | returns the number of interpolations points -1 |
| EvaluatePhi | evaluates a single Lagrange interpolation polynomial |
Methods of TriangleQuadrature :
| ConstructQuadrature | computes quadrature formulas for the unit triangle |
| GetTensorizedQuadratureRule | computes tensorized quadrature formulas for the unit triangle |
| CompleteTrianglePointsWithSymmetry | completes quadrature points and weights by exploiting symmetry |
Methods of QuadrangleQuadrature :
| ConstructQuadrature | computes quadrature formulas for the unit square |
| ConstructQuadrilateralNumbering | computes the numbering used in Montjoie for points in the unit square |
Methods of TetrahedronQuadrature :
| ConstructQuadrature | computes quadrature formulas for the unit tetrahedron |
| GetTensorizedQuadratureRule | computes tensorized quadrature formulas for the unit tetrahedron |
| CompleteTetrahedronPointsWithSymmetry | completes quadrature points and weights by exploiting symmetry |
Methods of PyramidQuadrature :
| ConstructQuadrature | computes quadrature formulas for the symmetry pyramid |
| ConstructPolynomialRule | computes quadrature formulas exact for polynomials |
Methods of HexahedronQuadrature :
| ConstructQuadrature | computes quadrature formulas for the unit cube |
| GetEdgeCube | fills the twelve edges of the unit cube |
| ConstructHexahedralNumbering | computes the numbering used in Montjoie for points in the unit cube |
Functions for quadrature rules :
| GetJacobiPolynomial | computes orthogonal Jacobi polynomials |
| EvaluateJacobiPolynomial | evaluates orthogonal Jacobi polynomials |
| SolveGauss | computes the roots of orthogonal polynomial |
| ComputeGaussLegendre | computes Gauss quadrature rule |
| ComputeGaussLobatto | computes Gauss-Lobatto quadrature rule |
| ComputeGaussJacobi | computes Gauss-Jacobi quadrature rule |
| ComputeGaussRadauJacobi | computes Gauss-Radau-Jacobi quadrature rule |
| ComputeGaussLobattoJacobi | computes Gauss-Lobatto-Jacobi quadrature rule |
| ComputeGaussChebyshev | computes Gauss-Chebyshev quadrature rule |
| ComputeGaussLogarithmic | computes Gauss quadrature rule with logarithmic weight |
| ComputeGaussLaguerre | computes Gauss-Laguerre quadrature rule |
| ComputeGaussHermite | computes Gauss-Hermite quadrature rule |
| ComputeGaussFormulas | computes Gauss-Lobatto or Gauss-Legendre quadrature rule |
| ComputeFourierCoef | computes coefficients for evaluating Legendre polynomials |
| ComputeLegendrePol_and_Derivative | evaluates Legendre polynomials and derivatives |
| ComputeGaussBlendedFormulas | computes blending of Gauss-Lobatto and Gauss-Legendre quadrature rule |
GetMemorySize
Syntax
size_t GetMemorySize() const;
This method returns the memory used by the object in bytes.
Example :
Globatto<Real_wp> lob; lob.ConstructQuadrature(3); // if you want to know the bytes used to store lob cout << "memory used by lob = " << lob.GetMemorySize() << endl;
Related topics :
GetNbPointsQuad
ConstructQuadrature
Location :
GetOrder, GetGeometryOrder
Syntax
int GetOrder() const; int GetGeometryOrder() const;
This method returns the order of quadrature. For example Gauss-Legendre quadrature rule of order r, will be exact for polynomials of degree 2r+1. Usually it is the order you specified when you called ConstructQuadrature.
Example :
Globatto<Real_wp> lob; lob.ConstructQuadrature(3); // GetOrder() should return 3 cout << "order = " << lob.GetOrder() << endl;
Related topics :
GetNbPointsQuad
ConstructQuadrature
Location :
GetNbPointsQuad
Syntax
int GetNbPointsQuad() const;
This method returns the number of quadrature points. The number of quadrature points is equal to order+1.
Example :
Globatto<Real_wp> lob; lob.ConstructQuadrature(5); // number of quadrature points : cout << "Number of quadrature points" << lob.GetNbPointsQuad() << endl;
Related topics :
Location :
ConstructQuadrature
Syntax
void ConstructQuadrature(int order); void ConstructQuadrature(int order, int type); void ConstructQuadrature(int order, int type, Real_wp a, Real_wp b);
This method computes a quadrature rule for an unit interval. The second argument is optional and specifies which rule will be constructed. If this argument is not present, Gauss-Legendre rule over [0,1] will be selected. The last arguments a and b are used if Gauss-Jacobi rules are constructed. With these rules, weights wi and points xi can be used to approximate the following integral:
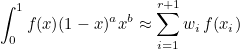
where f is a function and (1-x)a xb a given weight. The integration will be exact if f is a low-degree polynomial (below, we indicate the maximum degree depending on the chosen rule). The default values of a and b are equal to 0 (no weight). The following types are available. Gauss-Lobatto rules include extremities 0 and 1, whereas Gauss-Radau rules include the extremity 0.
- QUADRATURE_GAUSS (default) : Gauss-Legendre quadrature rules exact for polynomials of degree ≤ 2r+1
- QUADRATURE_LOBATTO : Gauss-Lobatto quadrature rules exact for polynomials of degree ≤ 2r-1
- QUADRATURE_RADAU : Gauss-Radau quadrature rules exact for polynomials of degree ≤ 2r
- QUADRATURE_JACOBI : Gauss-Jacobi quadrature rules exact for polynomials of degree ≤ 2r+1
- QUADRATURE_RADAU_JACOBI : Gauss-Radau-Jacobi quadrature rules exact for polynomials of degree ≤ 2r
- QUADRATURE_LOBATTO_JACOBI : Gauss-Lobatto-Jacobi quadrature rules exact for polynomials of degree ≤ 2r-1
- QUADRATURE_GAUSS_BLENDED : blending of Gauss-Lobatto rules and Gauss-Legendre rules
- QUADRATURE_GAUSS_SQUARED : Gauss-Legendre rules with a change of variable x = y2
Gauss-squared are based on a change of variable x = y2 such that the integral over the unit interval becomes
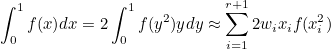
where xi and wi are Gauss-Legendre points
and weights. Therefore, the Gauss-squared points and weights are
equal to xi2 and 2 wi
xi. Such rules integrate exactly a singularity in
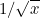 .
.
Blending of Gauss-Lobatto and Gauss-Legendre rules is explained by
Mark Ainsworth and Hafiz Abdul Wajid (Optimally Blended
Spectral-Finite Element Scheme for Wave Propagation and Non-Standard
Reduced Integration). The blending parameter τ is stored in the
static attribute of Globatto (Globatto<Real_wp>::blending_default). If
this attribute is not modified, τ will be chosen as
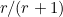 which is the optimal value for dispersion error (for wave equation).
which is the optimal value for dispersion error (for wave equation).
Example :
// 1-D integration with Gauss points Globatto<Real_wp> lob; int r = 3; lob.ConstructQuadrature(r); // 1-D integration with Gauss-Lobatto points lob.ConstructQuadrature(r, lob.QUADRATURE_LOBATTO); // if you want to integrate \int f (1-x)^a x^b Real_wp a = 1, b = 2; lob.ConstructQuadrature(r, lob.QUADRATURE_JACOBI, a, b);
Related topics :
Location :
AffectPoints
Syntax
void AffectPoints(const Vector<double>& points);
This method replaces quadrature points of the object by the points you provide. Quadrature weights are not modified by this fonction. The aim of this function is that you are able to use methods related to Lagrange interpolation polynomials based on the points you entered : Evaluate, EvaluatePhiGrad and ComputeValuesPhiRef.
Example :
// you define points for Lagrange interpolation polynomials Vector<double> points(4); points(0) = 0.0; points(1) = 0.3; points(2) = 0.7; points(3) = 1.0; // then you construct Lagrange interpolation polynomials Globatto<double> lob; lob.AffectPoints(points); // then you can evaluate basis functions based on these points Vector<double> phi; double x = 0.56; lob.ComputeValuesPhiRef(x, phi);
Related topics :
Location :
AffectWeights
Syntax
void AffectWeights(const Vector<double>& weights);
This method replaces quadrature weights of the object by the weights you provide.
Example :
// you define quadrature points and weights Vector<double> points(4), weights(4); points(0) = 0.0; points(1) = 0.3; points(2) = 0.7; points(3) = 1.0; weights(0) = 0.1; weights(1) = 0.4; weights(2) = 0.4; weights(3) = 0.1; // then you can store this formula in the object lob Globatto<double> lob; lob.AffectPoints(points); lob.AffectWeights(weights); // arrays are copied, you can clear the arguments if you want points.Clear(); weights.Clear(); // and use this quadrature rule Real_wp intF = 0; for (int i = 0; i < 4; i++) intF = f(lob.Points(i)) * lob.Weights(i);
Related topics :
Location :
Points, Weights
Syntax
double Points(int i) const; double Weights(int i) const; const Vector<double>& Points() const; const Vector<double>& Weights() const;
These methods returns the quadrature points or weights over the unit interval [0,1]. You can also get the vector containing all the points or all the weights.
Example :
// first you construct quadrature/interpolation points Globatto<Real_wp> lob; lob.ConstructQuadrature(4, lob.QUADRATURE_LOBATTO); // then you can select a single point/weight double x1 = lob.Points(1); double w1 = lob.Weights(1); // or retrieve all the points/weights Vector<double> points, weights; points = lob.Points(); weights = lob.Weights();
Location :
EvaluatePhi
Syntax
double EvaluatePhi(int i, const double& x);
This method evaluates a Lagrange interpolation polynomial at a given point. The interpolation points we consider are the quadrature points of the object, then the Lagrange interpolation polynomials can be written:
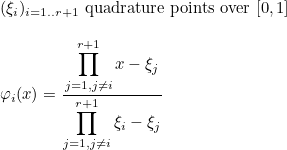
Example :
// first you construct quadrature/interpolation points Globatto<Real_wp> lob; lob.ConstructQuadrature(4, lob.QUADRATURE_LOBATTO); // then you can evaluate basis functions based on these points int i = 1; double x = 0.56; double val = lob.EvaluatePhi(i, x); // and derivatives double dval = lob.EvaluatePhiGrad(i, x);
Related topics :
ConstructQuadrature
EvaluatePhiGrad
Location :
EvaluatePhiGrad
Syntax
double EvaluatePhiGrad(int i, const double& x);
This method evaluates the derivative of a Lagrange interpolation polynomial at a given point. The interpolation points we consider are the quadrature points of the object, then the Lagrange interpolation polynomials can be written :
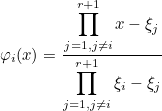
Example :
// first you construct quadrature/interpolation points Globatto<Real_wp> lob; lob.ConstructQuadrature(4, lob.QUADRATURE_LOBATTO); // then you can evaluate basis functions based on these points int i = 1; double x = 0.56; double val = lob.EvaluatePhi(i, x); // and derivatives double dval = lob.EvaluatePhiGrad(i, x);
Related topics :
Location :
GradPhi
Syntax
double GradPhi(int i, int j) const; const Matrix<double>& GradPhi() const;
This method returns the matrix A containing the derivatives of Lagrange interpolation polynomials at these same points.
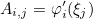
It can be also used to know an element of this matrix A.
Example :
// first you construct quadrature/interpolation points Globatto<Real_wp> lob; lob.ConstructQuadrature(4, lob.QUADRATURE_LOBATTO); // then you compute derivatives on the same interpolation points lob.ComputeGradPhi(); // and copy them for example Matrix<Real_wp> dGL_GL = lob.GradPhi(); // if you do not want to copy them, you can also to an element of the matrix // dphi_i'(xi_j) int i = 1, j = 2; dPhi_dxj = lob.GradPhi(i, j);
Related topics :
ComputeGradPhi
EvaluatePhiGrad
Location :
ComputeValuesPhiRef
Syntax
void ComputeValuesPhiRef(Real_wp x, VectReal_wp& phi);
This method evaluates the Lagrange interpolation polynomials at a given point. The interpolation points we consider are the quadrature points of the object, then the Lagrange interpolation polynomials can be written:
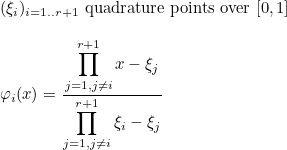
It should be more efficient to call this method (rather than EvaluatePhi) if all basis functions need to be evaluated.
Example :
// first you construct quadrature/interpolation points Globatto<Real_wp> lob; lob.ConstructQuadrature(4, lob.QUADRATURE_LOBATTO); // then you can evaluate basis functions based on these points VectReal_wp phi; Real_wp x = 0.56; lob.ComputeValuesPhiRef(x, phi); // values of basis functions are stored in the array phi
Related topics :
ConstructQuadrature
EvaluatePhiGrad
Location :
ComputeGradPhi
Syntax
void ComputeGradPhi();
This method computes the array containing the derivatives of Lagrange interpolation polynomials at these same points. You can retrieve these values with the method GradPhi.
Example :
// first you construct quadrature/interpolation points Globatto<Real_wp> lob; lob.ConstructQuadrature(4, lob.QUADRATURE_LOBATTO); // then you compute derivatives on the same interpolation points lob.ComputeGradPhi(); // and copy them for example Matrix<Real_wp> dGL_GL = lob.GradPhi();
Related topics :
Location :
Points
Syntax
Real_wp Points(int i) const;
This method returns an interpolation point stored in the object.
Example :
// first you initialize the object // the interval [0, 1] is subdivided in n subdivisions // on each subdivision, r+1 interpolation points are used SubdivGlobatto lob; int n = 3, r = 5; lob.Init(false, n, r); // number of interpolation points (in all the interval [0, 1] int nb_points = lob.GetOrder() + 1; // then you can write all these points for (int i = 0; i < nb_points; i++) cout << "Point : " << lob.Points(i) << endl;
Related topics :
Location :
Init
Syntax
void Init(bool regular, int n, int r); void Init(bool regular, int n, int type_quad);
This method initializes a regular subdivion of the interval [0, 1] (n subdivisions) with r+1 Gauss-Lobatto points on each subdivision. If regular is true, r+1 regular points are used instead of Gauss-Lobatto points. The last argument is optional and indicate the quadrature points to use (instead of Gauss-Lobatto points). The integer has to be chosen accordingly to the list presented in the function ConstructQuadrature.
Example :
// first you initialize the object // the interval [0, 1] is subdivided in n subdivisions // on each subdivision, r+1 interpolation points are used SubdivGlobatto lob; int n = 3, r = 5; lob.Init(false, n, r); // number of interpolation points (in all the interval [0, 1] int nb_points = lob.GetOrder() + 1; // then you can evaluate basis functions based on this set of points Real_wp x = 0.56; VectReal_wp phi(nb_points); for (int i = 0; i < nb_points; i++) phi(i) = lob.EvaluatePhi(i, x); // you can also choose other points than Gauss-Lobatto (e.g. Chebyshev points) lob.Init(false, n, r, Globatto<Real_wp>::TCHEBYSHEV);
Related topics :
Location :
InitPoints
Syntax
void InitPoints(n, Vector& points);
This method initializes a regular subdivion of the interval [0, 1] (n subdivisions) with given points on each subdivision.
Example :
// first you initialize the object // the interval [0, 1] is subdivided in n subdivisions // on each subdivision, the same points are used, they are provided by the user Vector<double> pts(4); pts(0) = 0.0; pts(1) = 0.2; pts(2) = 0.8; pts(3) = 1.0; SubdivGlobatto lob; lob.InitPoints(n, pts); // then you can evaluate basis functions based on this subdivision Real_wp x = 0.56; VectReal_wp phi(nb_points); for (int i = 0; i < nb_points; i++) phi(i) = lob.EvaluatePhi(i, x);
Related topics :
Location :
EvaluatePhi
Syntax
Real_wp EvaluatePhi(int i, const Real_wp& x);
This method evaluates a Lagrange interpolation polynomial at a given point.
Example :
// first you initialize the object // the interval [0, 1] is subdivided in n subdivisions // on each subdivision, r+1 interpolation points are used SubdivGlobatto lob; int n = 3, r = 5; lob.Init(false, n, r); // number of interpolation points (in all the interval [0, 1] int nb_points = lob.GetOrder() + 1; // then you can evaluate basis functions based on this set of points Real_wp x = 0.56; VectReal_wp phi(nb_points); for (int i = 0; i < nb_points; i++) phi(i) = lob.EvaluatePhi(i, x);
Related topics :
Location :
ConstructQuadrature
Syntax
void ConstructQuadrature(int p, VectR3& points, VectReal_wp& weights); void ConstructQuadrature(int p, VectR3& points, VectReal_wp& weights, int type_quad); void ConstructQuadrature(int p, VectR3& points, VectReal_wp& weights, int type_quad, Real_wp a, Real_wp b);
This static method computes the 3-D cubature points and associated weights. The constructed cubature formula can be used to integrate a function over the unit cube. This formula is based on a tensorization of 1-D quadrature points. The optional argument type_quad is the type of quadrature (see the method ConstructQuadrature of the class Globatto). The optional arguments a and b are the parameters for Gauss-Jacobi points.
Example :
// for Gauss-Legendre cubature rules VectR3 points; VectReal_wp weights; HexahedronQuadrature::ConstructQuadrature(5, points, weights); // you can compute the integral of a 3-D function Real_wp intF = 0; for (int i = 0; i < points.GetM(); i++) intF = f(points(i)) * weights(i); // you can use other 1-D quadrature rules to construct the 3-D rules HexahedronQuadrature::ConstructQuadrature(5, points, weights, Globatto<Real_wp>::QUADRATURE_RADAU);
Related topics :
Location :
GetEdgeCube
Syntax
void GetEdgeCube(Matrix<int>& hex_edge);
This static method fills the two edges of the unit cube with the numbering used by Montjoie.
Example :
Matrix<int> hex_edge; HexahedronQuadrature::GetEdgeCube(hex_edge); // two extremities of edge 5 for example : int n1 = hex_edge(5, 0), n2 = hex_edge(5, 1);
Location :
ConstructHexahedralNumbering
Syntax
void ConstructHexahedralNumbering(int r, Array3D<int>& NumNodes3D, Matrix<int>& CoordinateNodes);
This static method fills the numbering used for 3-D cubature points..
Example :
// for Gauss-Legendre cubature rules
VectR3 points; VectReal_wp weights;
int r = 5;
HexahedronQuadrature::ConstructQuadrature(r, points, weights);
// points are obtained by tensorization
// (i, j, k) => scalar n can be obtained
Array3D<int> NumNodes3D;
Matrix<int> CoordinateNodes;
HexahedronQuadrature::ConstructHexahedralNumbering(r, NumNodes3D, CoordinatesNodes);
// loop over each coordinate
for (int i = 0; i ≤ r; i++)
for (int j = 0; j ≤ r; j++)
for (int k = 0; k ≤ r; k++)
{
int n = NumNodes3D(i, j, k);
R3 pt = points(n);
// i, j and k are equal to CoordinateNodes(n, 0:2)
}
Location :
ConstructQuadrature
Syntax
void ConstructQuadrature(int p, VectR3& points, VectReal_wp& weights, VectReal_wp& points_z, VectReal_wp& weights_z, int type_quad);
This static method computes the 3-D cubature points and associated weights. The constructed cubature formula can be used to integrate a function over the symmetric pyramid. Some formulas are based on a tensorization of 1-D quadrature points over the unit cube, which then is transformed into the symmetric pyramid (with a Duffy transformation) to obtain points in the pyramid. The optional argument type_quad is the type of quadrature to use to choose between the following list :
- QUADRATURE_GAUSS : tensorized Gauss-Legendre rules in the three directions (x, y, z)
- QUADRATURE_JACOBI1 : tensorized Gauss-Legendre rules x, y and Gauss-Jacobi rules in z with a weight (1-z)
- QUADRATURE_JACOBI2 : tensorized Gauss-Legendre rules x, y and Gauss-Jacobi rules in z with a weight (1-z)2
- QUADRATURE_NON_PRODUCT : cubature rules that integrate exactly polynomials
If QUADRATURE_NON_PRODUCT is chosen, the method ConstructPolynomialRule is called. If QUADRATURE_JACOBI1 or QUADRATURE_JACOBI2 are chosen the function to integrate is assumed to be regular when transformed in the unit cube.
Example :
// for Gauss-Legendre cubature rules VectR3 points; VectReal_wp weights; VectReal_wp points_z, weights_z; PyramidQuadrature::ConstructQuadrature(5, points, weights, points_z, weights_z, PyramidQuadrature::QUADRATURE_JACOBI2); // you can compute the integral of a 3-D function over the symmetric pyramid Real_wp intF = 0; for (int i = 0; i < points.GetM(); i++) intF = f(points(i)) * weights(i);
Related topics :
Location :
ConstructPolynomialRule
Syntax
void ConstructPolynomialRule(int p, VectR3& points, VectReal_wp& weights);
This static method computes the 3-D cubature points and associated weights. The constructed cubature formula can be used to integrate a function over the symmetric pyramid. The formula will integrate exactly polynomials of degree less or equal to p.
Example :
// for polynomial rules // you specify the degree you want to integrate exactly int p = 6; VectR3 points; VectReal_wp weights; PyramidQuadrature::ConstructPolynomialRule(p, points, weights); // you can compute the integral of a 3-D function over the symmetric pyramid Real_wp intF = 0; for (int i = 0; i < points.GetM(); i++) intF = f(points(i)) * weights(i);
Related topics :
Location :
ConstructQuadrature
Syntax
void ConstructQuadrature(int p, VectR2& points, VectReal_wp& weights); void ConstructQuadrature(int p, VectR2& points, VectReal_wp& weights, int type_quad); void ConstructQuadrature(int p, VectR2& points, VectReal_wp& weights, int type_quad, Real_wp a, Real_wp b);
This static method computes the 2-D quadrature points and associated weights. The constructed quadrature formula can be used to integrate a function over the unit square. This formula is based on a tensorization of 1-D quadrature points. The optional argument type_quad is the type of quadrature (see the method ConstructQuadrature of the class Globatto). The optional arguments a and b are the parameters for Gauss-Jacobi points.
Example :
// for Gauss-Legendre quadrature rules VectR2 points; VectReal_wp weights; QuadrangleQuadrature::ConstructQuadrature(5, points, weights); // you can compute the integral of a 2-D function Real_wp intF = 0; for (int i = 0; i < points.GetM(); i++) intF = f(points(i)) * weights(i); // you can use other 1-D quadrature rules to construct the 2-D rules QuadrangleQuadrature::ConstructQuadrature(5, points, weights, Globatto<Real_wp>::QUADRATURE_RADAU);
Related topics :
Location :
ConstructQuadrilateralNumbering
Syntax
void ConstructQuadrilateralNumbering(int r, Matrix<int>& NumNodes2D, Matrix<int>& CoordinateNodes);
This static method fills the numbering used for 2-D quadrature points..
Example :
// for Gauss-Legendre quadrature rules
VectR3 points; VectReal_wp weights;
int r = 5;
QuadrangleQuadrature::ConstructQuadrature(r, points, weights);
// points are obtained by tensorization
// (i, j) => scalar n can be obtained
Matrix<int> NumNodes2D;
Matrix<int> CoordinateNodes;
QuadrangleQuadrature::ConstructHexahedralNumbering(r, NumNodes2D, CoordinatesNodes);
// loop over each coordinate
for (int i = 0; i ≤ r; i++)
for (int j = 0; j ≤ r; j++)
{
int n = NumNodes2D(i, j);
R2 pt = points(n);
// i, j are equal to CoordinateNodes(n, 0:1)
}
Location :
ConstructQuadrature
Syntax
void ConstructQuadrature(int p, VectR2& points, VectReal_wp& weights); void ConstructQuadrature(int p, VectR2& points, VectReal_wp& weights, int type_quad);
This static method computes the 2-D quadrature points and associated weights. The constructed quadrature formula can be used to integrate a function over the unit triangle. Some formulas are based on a tensorization of 1-D quadrature points over the unit triangle, which then is transformed into the unit triangle (with a Duffy transformation) to obtain points in the pyramid. The optional argument type_quad is the type of quadrature to use to choose between the following list :
- QUADRATURE_GAUSS (default) : symmetric rules that integrate polynomials of degree p
- QUADRATURE_TENSOR : tensorized Gauss-Legendre rules
- QUADRATURE_MASS_LUMPED : symmetric rules that achieve mass lumping
- QUADRATURE_QUASI_LUMPED : symmetric rules that achieve quasi mass lumping
Example :
// for symmetric rules that integrate exactly polynomials of degree <= p int p = 10; VectR2 points; VectReal_wp weights; TriangleQuadrature::ConstructQuadrature(p, points, weights); // you can compute the integral of a 2-D function over the unit triangle Real_wp intF = 0; for (int i = 0; i < points.GetM(); i++) intF = f(points(i)) * weights(i);
Location :
GetTensorizedQuadratureRule
Syntax
void GetTensorizedQuadratureRule(int r, VectR2& points, VectReal_wp& weights);
This static method computes the 2-D quadrature points and associated weights. The constructed quadrature formula can be used to integrate a function over the unit triangle. This formula is based on a tensorization of 1-D quadrature points over the unit triangle, which then is transformed into the unit triangle (with a Duffy transformation) to obtain points in the pyramid.
Example :
// for tensorized rules, you give the order r (r+1 Gauss points in each direction) // polynomials of degree 2r+1 should be integrated exactly int r = 5; VectR2 points; VectReal_wp weights; TriangleQuadrature::GetTensorizedQuadratureRule(p, points, weights); // you can compute the integral of a 2-D function over the unit triangle Real_wp intF = 0; for (int i = 0; i < points.GetM(); i++) intF = f(points(i)) * weights(i);
Location :
CompleteTrianglePointsWithSymmetry
Syntax
void CompleteTrianglePointsWithSymmetry(VectR2& points, VectReal_wp& weights, int nb_tuples, const IVect& size_tuple);
This static method completes quadrature points over the unit triangle by symmetry. This internal method should not be called in a regular use.
Location :
ConstructQuadrature
Syntax
void ConstructQuadrature(int p, VectR3& points, VectReal_wp& weights); void ConstructQuadrature(int p, VectR3& points, VectReal_wp& weights, int type_quad);
This static method computes the 3-D cubature points and associated weights. The constructed cubature formula can be used to integrate a function over the unit tetrahedron. Some formulas are based on a tensorization of 1-D quadrature points over the unit cube, which then is transformed into the unit tetrahedron (with a Duffy transformation) to obtain points in the tetrahedron. The optional argument type_quad is the type of quadrature to use to choose between the following list :
- QUADRATURE_GAUSS (default) : symmetric rules that integrate polynomials of degree p
- QUADRATURE_TENSOR : tensorized Gauss-Legendre rules
- QUADRATURE_MASS_LUMPED : symmetric rules that achieve mass lumping
- QUADRATURE_QUASI_LUMPED : symmetric rules that achieve quasi mass lumping
Example :
// for symmetric rules that integrate exactly polynomials of degree <= p int p = 10; VectR3 points; VectReal_wp weights; TetrahedronQuadrature::ConstructQuadrature(p, points, weights); // you can compute the integral of a 3-D function over the unit tetrahedron Real_wp intF = 0; for (int i = 0; i < points.GetM(); i++) intF = f(points(i)) * weights(i);
Location :
CompleteTetrahedronPointsWithSymmetry
Syntax
void CompleteTetrahedronPointsWithSymmetry(VectR3& points, VectReal_wp& weights, int nb_tuples, const IVect& size_tuple);
This static method completes quadrature points over the unit tetrahedron by symmetry. This internal method should not be called in a regular use.
Location :
GetJacobiPolynomial
Syntax
void GetJacobiPolynomial(Matrix<double>& ab, int n, double alpha, double beta);
This function computes the recurrence relations for orthogonal polynomial with a jacobi weight, i.e. it constructs polynomials Pn so that
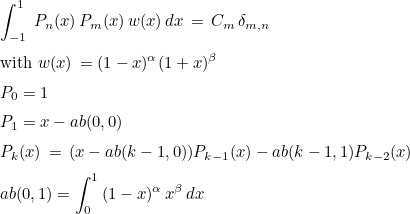
You have noticed that those polynomials are proportional with Jacobi polynomials but not identical. The polynomials constructed here are called monic Jacobi polynomials, since the coefficient of the term of highest degree is equal to 1.
Example :
// orthogonal polynomials with respect to (1-x)^2 (1+x) Matrix<double> ab; int n = 3; double alpha = 2.0, beta = 1.0; // we compute P_0, P_1, P_2, ..., P_n GetJacobiPolynomial(ab, n, alpha, beta); // then you can evaluate those polynomials at a point x double x = -0.5; Vector<double> Pn; // Pn(0) = P_1(x), Pn(1) = P_2(x), ... Pn(n-1) = P_n(x) EvaluateJacobiPolynomial(ab, n, x, Pn); // you can evaluate polynomials and their derivatives Vector<double> dPn; // dPn(0) = P'_1(x), dPn(1) = P'_2(x), ... dPn(n-1) = P'_n(x) EvaluateJacobiPolynomial(ab, n, x, Pn, dPn);
Location :
EvaluateJacobiPolynomial
Syntax
double EvaluateJacobiPolynomial(const Matrix<double>& ab, int m, double x); void EvaluateJacobiPolynomial(const Matrix<double>& ab, int n, double x, Vector<double>& Pn); void EvaluateJacobiPolynomial(const Matrix<double>& ab, int n, double x, Vector<double>& Pn, Vector<double>& dPn);
This function evaluates the polynomials constructed by the function GetJacobiPolynomial at a given point. If five arguments are provided, this will compute derivatives too and write them in the last argument.
Example :
// orthogonal polynomials with respect to (1-x)^2 (1+x) Matrix<double> ab; int n = 3; double alpha = 2.0, beta = 1.0; // we compute P_0, P_1, P_2, ..., P_n GetJacobiPolynomial(ab, n, alpha, beta); // then you can evaluate those polynomials at a point x double x = -0.5; Vector<double> Pn; // Pn(0) = P_1(x), Pn(1) = P_2(x), ... Pn(n-1) = P_n(x) EvaluateJacobiPolynomial(ab, n, x, Pn); // you can evaluate polynomials and their derivatives Vector<double> dPn; // dPn(0) = P'_1(x), dPn(1) = P'_2(x), ... dPn(n-1) = P'_n(x) EvaluateJacobiPolynomial(ab, n, x, Pn, dPn); // you can also ask the value of a single polynomial (P_2 here) Real_wp val = EvaluateJacobiPolynomial(ab, 2, x);
Location :
SolveGauss
Syntax
void SolveGauss(Vector<double>& x, Vector<double>& w, int n, double alpha, double beta, const Matrix<double>& ab);
This function computes the roots of the last orthogonal polynomial related to Jacobi weight. On output, w will contain quadrature weights (of the associated Gauss-Jacobi integration rule), and x the roots. Be careful because the roots are shifted, so that they belong to [0,1] instead of [-1,1] the interval where orthogonal polynomials are defined. Similarly, the quadrature weights are defined on the interval [0,1].
Example :
// orthogonal polynomials with respect to (1-x)^2 (1+x) on [-1,1] Matrix<double> ab; int n = 3; double alpha = 2.0, beta = 1.0; // we compute P_0, P_1, P_2, ..., P_n GetJacobiPolynomial(ab, n, alpha, beta); // then you can find roots of Pn, but they are shifted on interval [0,1] Vector<double> points, weights; SolveGauss(points, weights, n, alpha, beta, ab);
Location :
ComputeGaussLegendre
Syntax
void ComputeGaussLegendre(Vector<double>& x, Vector<double>& w, int n);
This function computes Gauss-Legendre quadrature formulas on [0,1]. You can use those formulas to compute an integral :
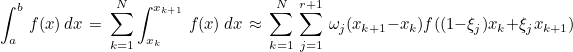
Example :
// you specify order
int r = 3;
// compute Gauss formulas
Vector<double> points, weights;
ComputeGaussLegendre(points, weights, r);
// and then compute the integral of 1/(1+x^2) between a and b
double a = -3, b = 2; int N = 10;
double xk, xkp1, h = (b-a)/N;
double eval_int = 0, evalf, x;
for (int k = 0; k < N; k++)
{
xk = a + h*k;
xkp1 = xk + h;
for (int j = 0; j <= r; j++)
{
x = (1-points(j))*xk + points(j)*xkp1;
evalf = 1.0/(1.0+x*x);
eval_int += weights(j)*h*evalf;
}
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussLobatto
Syntax
void ComputeGaussLobatto(Vector<double>& x, Vector<double>& w, int n);
This function computes Gauss-Lobatto quadrature formulas on [0,1]. You can use those formulas to compute an integral :
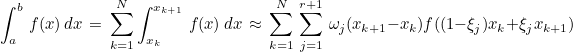
Gauss-Lobatto formulas include extremities 0 and 1, whereas Gauss formulas don't include those extremities but are more accurate than Gauss-Lobatto formulas.
Example :
// you specify order
int r = 3;
// compute Gauss-Lobatto formulas
Vector<double> points, weights;
ComputeGaussLobatto(points, weights, r);
// and then compute the integral of 1/(1+x^2) between a and b
double a = -3, b = 2; int N = 10;
double xk, xkp1, h = (b-a)/N;
double eval_int = 0, evalf, x;
for (int k = 0; k < N; k++)
{
xk = a + h*k;
xkp1 = xk + h;
for (int j = 0; j <= r; j++)
{
x = (1-points(j))*xk + points(j)*xkp1;
evalf = 1.0/(1.0+x*x);
eval_int += weights(j)*h*evalf;
}
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussJacobi
Syntax
void ComputeGaussJacobi(Vector<double>& x, Vector<double>& w, int n, double alpha, double beta);
This function computes Gauss-Jacobi quadrature formulas on [0,1]. You can use those formulas to compute a weighted integral :
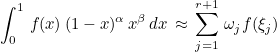
Example :
// you specify order
int r = 3;
// compute Gauss-Jacobi formulas
double alpha = 2.0, beta = 1.0;
Vector<double> points, weights;
ComputeGaussJacobi(points, weights, r, alpha, beta);
// and then compute the integral of (1-x)^2 x / (1+x^2) between 0 and 1
double eval_int = 0, x;
for (int j = 0; j <= r; j++)
{
x = points(j);
evalf = 1.0/(1.0+x*x);
eval_int += weights(j)*h*evalf;
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussRadauJacobi
Syntax
void ComputeGaussRadauJacobi(Vector<double>& x, Vector<double>& w, int n, double alpha, double beta, bool right_ext);
This function computes Gauss-Radau-Jacobi quadrature formulas on [0,1]. You can use those formulas to compute a weighted integral :
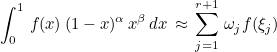
Gauss-Radau-Jacobi rules include an extremity (0 or 1) but are less accurate than Gauss-Jacobi rules.
Example :
// you specify order
int r = 3;
// compute Gauss-Radau-Jacobi formulas with the right extremity (1)
double alpha = 2.0, beta = 1.0;
Vector<double> points, weights;
ComputeGaussRadauJacobi(points, weights, r, alpha, beta, true);
// and then compute the integral of (1-x)^2 x / (1+x^2) between 0 and 1
double eval_int = 0, x;
for (int j = 0; j <= r; j++)
{
x = points(j);
evalf = 1.0/(1.0+x*x);
eval_int += weights(j)*h*evalf;
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussLobattoJacobi
Syntax
void ComputeGaussLobattoJacobi(Vector<double>& x, Vector<double>& w, int n, double alpha, double beta);
This function computes Gauss-Lobatto-Jacobi quadrature formulas on [0,1]. You can use those formulas to compute a weighted integral :
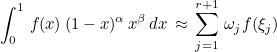
Gauss-Lobatto-Jacobi rules include the two extremities (0 and 1) but are less accurate than Gauss-Jacobi rules.
Example :
// you specify order
int r = 3;
// compute Gauss-Lobatto-Jacobi formulas
double alpha = 2.0, beta = 1.0;
Vector<double> points, weights;
ComputeGaussLobattoJacobi(points, weights, r, alpha, beta, true);
// and then compute the integral of (1-x)^2 x / (1+x^2) between 0 and 1
double eval_int = 0, x;
for (int j = 0; j <= r; j++)
{
x = points(j);
evalf = 1.0/(1.0+x*x);
eval_int += weights(j)*h*evalf;
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussChebyshev
Syntax
void ComputeGaussChebyshev(Vector<double>& x, Vector<double>& w, int n);
This function computes Gauss-Chebyshev quadrature formulas on [0,1]. You can use those formulas to compute a weighted integral :
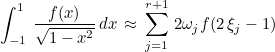
Example :
// you specify order
int r = 3;
// compute Gauss-Chebyshev formulas
Vector<double> points, weights;
ComputeGaussChebyshev(points, weights, r);
// and then compute the integral of (1-x)^2 x / sqrt(1-x^2) between -1 and 1
double eval_int = 0, x;
for (int j = 0; j <= r; j++)
{
x = 2.0*points(j)-1;
evalf = square(1.0-x)*x;
eval_int += 2.0*weights(j)*h*evalf;
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussLogarithmic
Syntax
void ComputeGaussLogarithmic(Vector<double>& x, Vector<double>& w, int n, double a);
This function computes Gauss-Logarithmic quadrature formulas on [0,1]. You can use those formulas to compute a weighted integral (with a logarithmic weight) :
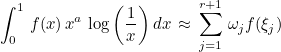
Example :
// you specify order
int r = 3;
// compute Gauss-Chebyshev formulas
double a = -0.5;
Vector<double> points, weights;
ComputeGaussLogarithmic(points, weights, r, a);
// and then compute the integral of (1-x)^2 x * x^a log(1/x) between 0 and 1
double eval_int = 0, x;
for (int j = 0; j <= r; j++)
{
x = points(j);
evalf = square(1.0-x)*x;
eval_int += weights(j)*h*evalf;
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussLaguerre
Syntax
void ComputeGaussLaguerre(Vector<double>& x, Vector<double>& w, int n, double a);
This function computes Gauss-Laguerre quadrature formulas on [0, +∞[. You can use those formulas to compute a weighted integral (with an exponential weight) :
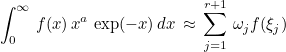
Example :
// you specify order
int r = 3;
// compute Gauss-Laguerre formulas
double a = -0.5;
Vector<double> points, weights;
ComputeGaussLaguerre(points, weights, r, a);
// and then compute the integral of (1-x)^2 x * x^a exp(-x) between 0 and 1
double eval_int = 0, x;
for (int j = 0; j <= r; j++)
{
x = points(j);
evalf = square(1.0-x)*x;
eval_int += weights(j)*h*evalf;
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussHermite
Syntax
void ComputeGaussHermite(Vector<double>& x, Vector<double>& w, int n, double a);
This function computes Gauss-Laguerre quadrature formulas on ]-∞,+∞[. You can use those formulas to compute a weighted integral (with an exponential weight) :
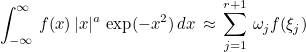
Example :
// you specify order
int r = 3;
// compute Gauss-Hermite formulas
double a = -0.5;
Vector<double> points, weights;
ComputeGaussHermite(points, weights, r, a);
// and then compute the integral of (1-x)^2 x * x^a exp(-x^2) in R
double eval_int = 0, x;
for (int j = 0; j <= r; j++)
{
x = points(j);
evalf = square(1.0-x)*x;
eval_int += weights(j)*h*evalf;
}
cout << "value of the integral " << eval_int;
Location :
ComputeGaussFormulas
Syntax
void ComputeGaussFormulas(int nb_points, Vector<double>& x, Vector<double>& w, bool lobatto);
This function computes Gauss-Legendre or Gauss-Lobatto rules (if lobatto is true) by using Newton's method to find the roots of Legendre polynomials (or their derivatives). This function is called by ComputeGaussLegendre and ComputeGaussLobatto, so it is better to call directly one of these functions.
Example :
// number of Gauss points to compute int n = 2; // Gauss-Legendre formulas will integrate exactly polynomials // of degree lower or equal to 2n-1 VectReal_wp points, weights; ComputeGaussFormulas(n, points, weights, false);
Location :
ComputeFourierCoef
Syntax
void ComputeFourierCoef(int nb_points, Real_wp& cz, VectReal_wp& cp, VectReal_wp& dcp, VectReal_wp& ddcp);
This function computes the Fourier coefficient of the Legendre
polynomials
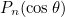 . Once this function is called, Legendre polynomials (and their
derivatives) can be evaluated for a given θ. This function is
only used by ComputeGaussFormulas, it should not be called directly.
. Once this function is called, Legendre polynomials (and their
derivatives) can be evaluated for a given θ. This function is
only used by ComputeGaussFormulas, it should not be called directly.
Example :
// degree of Legendre polynomial to evaluate (P_{n-1} will be evaluated)
int n = 3;
Real_wp cz;
VectReal_wp cp, dcp, ddcp;
ComputeFourierCoef(n, cz, cp, dcp, ddcp);
// Legendre polynomial P_{n-1} (cos teta), its derivative and second derivative
// are evaluated for a given value of teta
Real_wp teta = pi_wp/6;
Real_wp Pn, dPn, ddPn;
ComputeLegendrePol_and_Derivative(n, theta, cz, cp, dcp, ddcp, Pn, dPn, ddPn);
Location :
ComputeLegendrePol_and_Derivative
Syntax
void ComputeLegendrePol_and_Derivative(int nb_points, Real_wp teta, const Real_wp& cz, const VectReal_wp& cp, const VectReal_wp& dcp, const VectReal_wp& ddcp, Real_wp& Pn, Real_wp& dPn, Real_wp& ddPn);
This function evaluates a legendre polynomial for a given value of theta, assuming that ComputeFourierCoef has been called previously. This function is only used by ComputeGaussFormulas, it should not be called directly.
Example :
// degree of Legendre polynomial to evaluate (P_{n-1} will be evaluated)
int n = 3;
Real_wp cz;
VectReal_wp cp, dcp, ddcp;
ComputeFourierCoef(n, cz, cp, dcp, ddcp);
// Legendre polynomial P_{n-1} (cos teta), its derivative and second derivative
// are evaluated for a given value of teta
Real_wp teta = pi_wp/6;
Real_wp Pn, dPn, ddPn;
ComputeLegendrePol_and_Derivative(n, theta, cz, cp, dcp, ddcp, Pn, dPn, ddPn);
Location :
ComputeGaussBlendedFormulas
Syntax
void ComputeGaussBlendedFormulas(int nb_points, VectReal_wp& points, VectReal_wp& points, Real_wp tau);
This function evaluates a blending of Gauss and Gauss-Lobatto rules as defined by Mark Ainsworth.
Example :
int order = 4; // an interesting value of tau is r / (r+1) Real_wp tau = Real_wp(order)/(order+1); VectReal_wp points, weights; ComputeGaussBlendedFormulas(order+1, points, weights, tau);