How partial differential equations are specified in Montjoie
We describe here how equations are specified in Montjoie for 2-D and 3-D linear equations. We distinguish unknowns for which we can use H1 approximation (continuous finite elements), H(curl) approximation (so-called edge elements) or H(div) approximation (so-called facet elements). Moreover, you have to choose between a continuous formulation (with a possible mix of scalar and vectorial unknowns) and a Discontinuous Galerkin formulation (all the degrees of freedom are discontinuous for all unknowns). The choice between continuous or discontinous approximation has to be considered carefully. While discontinuous Galerkin formulations allow to obtain more reliable solutions with a control of spurious modes, these formulations induce less efficient computations (in terms of computational time and storage). H(curl) approximation is currently only used for Maxwell's equations.
In Montjoie, we consider that the unknowns are defined in all the computational domain and are solution of the same partial differential equation in this domain. Therefore, it is not "natural" to consider coupled problems with different partial differential equations in each part of the computational domain. In order to perform such operations, it is needed to introduce two objects EllipticProblem (or HyperbolicProblem for evolution problems), each object being devoted to the solution of a different set of partial differential equations. Such things are performed for fluid-structure problems and vibroacoustic problems, but there is no general class developed for coupled problems.
General formulation used for H1 approximation
When only scalar continuous finite elements are needed (to approximate Sobolev space H1), we are considering the following partial differential equations :
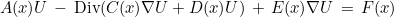
This form is quite general and can be used for a lot of problems. The unknown U can be scalar (i.e containing only one component) or vectorial (with several components). The tensors A(x), C(x), D(x) and E(x) can be constant or depending on space x, and on time t.
Variational formulation and how to specify a new set of equations
The variational formulation for continuous finite elements is the following one
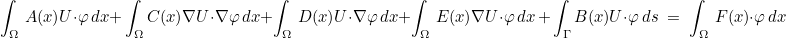
where operator B(x) is describing the boundary condition imposed on Γ (Dirichlet-to-Neumann operator). We can also consider more complicated boundary conditions (cf. the section devoted to Boundary conditions). If we have D=E* and if A and C are symmetric, the variational formulation is symmetric even if the numerical integration is not exact. If you to specify tensors A, C, D and E, it is needed to construct a class with the following prototype :
//! inheritance from GenericEquation
// use Real_wp if the equation needs to be solved with real numbers (instead of complex numbers)
class MyNewEquation
: public GenericEquation<Complex_wp>
{
public :
// number of unknowns = number of components for U
// use nb_unknowns_scal = nb_unknowns (except for DG formulation)
// nb_unknowns_vec greater than 0 if you want to add discontinuous unknowns (usually with a mixed formulation)
// nb_unknowns_hdg different from 0 for HDG (is equal to the number of components of Lagrange multipliers)
enum{nb_unknowns = 2, nb_components_en = 1, nb_components_hn = 1, nb_unknowns_scal = 2, nb_unknowns_vec = 0, nb_unknowns_hdg = 0};
static const bool FirstOrderFormulation = false;
static const bool DiscontinuousDiMatrix = false;
static const bool TensorStiffnessSymmetric = true;
// if you know that matrices are symmetric (global and/or elementary matrices)
inline static bool SymmetricGlobalMatrix() { return true; }
inline static bool SymmetricElementaryMatrix() { return true; }
// providing C in Cgrad_grad
template<class TypeEquation, class T0, class MatStiff>
static void GetGradGradTensor(const EllipticProblem<TypeEquation>& vars,
int i, int j, const GlobalGenericMatrix<T0>& nat_mat, int ref, MatStiff& Cgrad_grad);
// providing A in mass
template<class TypeEquation, class T0, class MatMass>
static void GetTensorMass(const EllipticProblem<TypeEquation>& vars,
int i, int j, const GlobalGenericMatrix<T0>& nat_mat, int ref, MatMass& mass);
// providing D and E in Dgrad_phi and Ephi_grad
template<class TypeEquation, class T0, class MatStiff>
static void GetGradPhiTensor(const EllipticProblem<TypeEquation>& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat, int ref, MatStiff& Dgrad_phi, MatStiff& Ephi_grad);
};
As you can see, you need to specify both the tensors A, C, D, and E. You can also provide products of these tensors with "vectors" by defining methods ApplyTensorMass,ApplyTensorStiffness, ApplyGradientUnknown and ApplyGradientFctTest. Since these functions are called a lot of times, it is important to optimize them by using precomputed arrays if needed, inlining them if they are placed in cxx files, and unrolling loops. The methods requiring products are actually used for matrix-vector product (if the matrix is not stored) whereas the methods requiring the tensors are used to compute the elementary matrices. As a result, if you are sure that you will only use direct solvers (usually more efficient especially in 2-D), you do not need to define the methods ApplyTensorMass,ApplyTensorStiffness, ApplyGradientUnknown and ApplyGradientFctTest. FirstOrderFormulation should be set to true if tensor C(x) is null (in which case you have only first-order derivatives in space). DiscontinuousDiMatrix and TensorStiffnessSymmetric are parameters used only for parallel execution, since continuous tensor D(x) and symmetric tensor C(x) are inducing lighter algorithms. For constant parameters (which are set once in the class, and are known at compilation) defined in the enum, we have the following convention :
- nb_unknowns : number of components (or unknowns) contained in U (e.g. 1 for Helmholtz equation, 2 for 2-D elastic equation, etc)
- type_element : type of finite element for the main mesh numbering (1 : scalar finite element, 2 : edge element, 3 : facet element). The default value is 1.
- nb_unknowns_en : number of components for the trace of u on surfaces
- nb_unknowns_hn : number of components for the trace of du/dn on surfaces
- nb_unknowns_scal : number of components which are continuous (usually equal to nb_unknowns)
- nb_unknowns_vec : number of components which are discontinuous, used for a mixed formulation
- nb_unknowns_hdg : number of components of the surface unknowns λ in HDG formulation
The integers nb_unknowns_scal and nb_unknowns_vec are used for unsteady problems, which are put into a first order problem through a mixed formulation. The constants nb_unknowns_en, nb_unknowns_hn are used when computing U and dU/dn on surfacic meshes (in order to write the correct number of components). The most important attributes are nb_unknowns and type_element. This last attribute is already set to 1 in the base class GenericEquation. So if you intend to use scalar finite elements for the main unknown, you do not need to redefine this attribute in the derived class.
GenericEquation
The class GenericEquation is the base class for all equations specified in Montjoie. This class is based on templates only (no virtual functions), such that only static methods are present. Details and explanations of methods in class GenericEquation are available below :
| ComputeDFjm1 | returns true if the inverse of the jacobian matrix DFi needs to be computed and stored |
| SymmetricGlobalMatrix | returns true if the global finite element matrix is symmetric |
| SymmetricElementaryMatrix | returns true if the elementary finite element matrix is symmetric |
| GetOtherElementType | returns the type of finite elements used to use for additional mesh numberings |
| ComputeMassMatrix | fills arrays needed to compute the elementary matrix |
| GetTensorMass | fills tensor A |
| ApplyTensorMass | Applies tensor A to a vector U |
| GetNeededDerivative | fills derivatives that need to be computed |
| GetGradGradTensor | fills tensor C |
| ApplyTensorStiffness | Applies tensor C to a matrix dU |
| GetGradPhiTensor | fills tensors D and E |
| ApplyGradientUnknown | Applies tensor E to a matrix dU |
| ApplyGradientFctTest | Applies tensor D to a vector U |
| GetNabc | Computes tensor appearing in DG formulations to treat boundary conditions |
| MltNabc | Applies tensor appearing in DG formulations to treat boundary conditions |
| GetPenalDG | Computes tensor appearing in DG formulations (penalty term) |
| MltPenalDG | Applies tensor appearing in DG formulations (penalty term) |
One you have defined a class for your equation, you add a branch for this new problem with the following code :
// you can derive from VarHarmonic
// but if your problem is close to another one (like Helmholtz or Maxwell)
// you could derive from this closer problem
template<class TypeEquation>
class MyNewProblem : public VarHarmonic<TypeEquation>
{
public :
// you can add attributes specific to the new equation
// usually the physical indices
VectReal_wp ref_lambda, ref_mu;
// you overload the methods you want
// for physical indices, usually we overload InitIndices and SetIndices
void InitIndices(int n);
int GetNbPhysicalIndices() const;
void SetIndices(int i, const Vector<string>& param);
// varying media (physical index that vary inside the element)
bool IsVaryingMedia(int i) const;
bool IsVaryingMedia(int m, int i) const;
void GetVaryingIndices(Vector<PhysicalVaryingMedia<Dimension, Complex_wp>* >& rho_complex, Vector<PhysicalVaryingMedia<Dimension, Real_wp>* >& rho_real,
IVect& num_ref, IVect& num_index, IVect& num_component, Vector<bool>& compute_grad,
Vector<bool>& compute_hess);
};
// then you create your specialized class EllipticProblem :
template<>
class EllipticProblem<MyNewEquation> : public MyNewProblem<TypeEquation>
{
public :
// elementary matrix
void ComputeElementaryMatrix(int i, IVect& num_dof, VirtualMatrix<Complex_wp>& mat_elem,
CondensationBlockSolver_Base<Complex_wp>&,
const GlobalGenericMatrix<Complex_wp>& nat_mat)
{
// you can use the "general" function (for scalar elements only)
Montjoie::ComputeElementaryMatrix(i, num_dof, mat_elem, nat_mat, *this, this->GetReferenceElementH1(i));
}
// numerical fluxes (for DG formulation)
void AddElementaryFluxesDG(VirtualMatrix<Complex_wp>& mat_sp,
const GlobalGenericMatrix<Complex_wp>& nat_mat,
int offset_row = 0, int offset_col = 0)
{
// general function
Montjoie::AddElementaryFluxesDG(mat_sp, nat_mat, *this, offset_row, offset_col);
}
};
Then in the executable file (.cc), you can use this new equation :
int main(int argc, char** argv)
{
InitMontjoie(argc, argv);
if (argc != 2)
{
cout << "Give a data file " << endl;
abort();
}
string input_file(argv[1]);
string type_element, type_equation;
getElement_Equation(file_name_data, type_element, type_equation);
EllipticProblem<MyNewEquation> vars;
vars.RunAll(input_file, type_element, type_equation);
}
Time-harmonic/Time-domain computations
The tensors A, C, D and E can depend on the space (variable x), but they may also involve time derivatives, for instance :
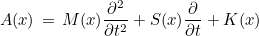
In time-harmonic domain, it would be transformed into :
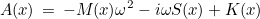
For time-harmonic computations, the tensors A(x), C(x), D(x) and E(x) are directly filled by using the pulsation (methods GetOmega(), GetSquareOmega() and GetMiomega()). For time-domain computations, we are only considering first and second-order derivatives in time. When the equations are only involving first derivatives (i.e. M(x) = 0), we say that the problem is of first-order. For implicit schemes, tensors C, D and E can contain derivatives in time, whereas explicit schemes are valid if only tensor A is involving derivatives in time. For implicit schemes, we need an intermediary object for the solution of a stationary-like problem when tensor A would be replaced by :
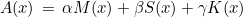
Coefficients α, β and γ are given by the time-scheme used. For example, for a Crank-Nicolson scheme (M(x) = 0), we would have
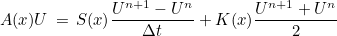
The linear system to solve involves only Un+1, so we would have to solve :
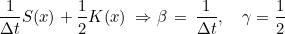
These coefficients α, β and γ are contained in object "GlobalGenericMatrix", through methods SetCoefMass/GetCoefMass (for α), SetCoefDamping/GetCoefDamping (for β) and SetCoefStiffness/GetCoefStiffness (for γ). For example, we show in the example below how to compute a matrix with different values of these coefficients.
// considering you have constructed an EllipticProblem object
void MyFunction(const EllipticProblem<TypeEquation>& var)
{
// then you declare a "GlobalGenericMatrix" object
GlobalGenericMatrix<Real_wp> nat_mat;
// you set coefficients contained in this object :
Real_wp dt = 0.01;
nat_mat.SetCoefMass(0);
nat_mat.SetCoefDamping(1.0/dt);
nat_mat.SetCoefStiffness(0.5);
// then you compute the finite element matrix with these coefficients
Matrix<Real_wp, General, ArrayRowSparse> A;
var.AddMatrixWithBC(A, nat_mat);
// matrix is computed, you can factorize it if you want
All_MatrixLU<Real_wp> mat_lu;
mat_lu.Factorize(A);
}
As a result, the specification of time-domain equations is containing the type of the associated stationary equation. There are also two other methods GetMassCoefficient/GetDampingCoefficient, which are used in discontinuous Galerkin methods for explicit schemes. Here an example of a new time-domain equation
class MyNewTimeEquation
{
public :
// associated stationary equation
typedef MyNewEquation TypeEquationStationary
// using real numbers
typedef Real_wp Complexe;
};
Unsteady problems are then derived with HyperbolicProblem class :
// usually it is derived from VarInstationary, but you could also
// derive from a closer class
template<class TypeEquation>
class MyNewTimeProblem : public VarInstationary<TypeEquation>
{
public :
// you may overload methods specific for this problem
// usually nothing to do if only the equation has changed
};
// and finally the HyperbolicProblem class :
template<>
class HyperbolicProblem<MyNewTimeEquation>
: public MyNewTimeProblem<MyNewTimeEquation>
{
// nothing to do
};
In the main file .cc, the object HyperbolicProblem is then used to launch the simulation.
General formulation used for Discontinuous Galerkin approximation
We are considering the same partial differential equations as for continuous approximation :
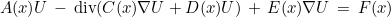
The variational formulation is classical :
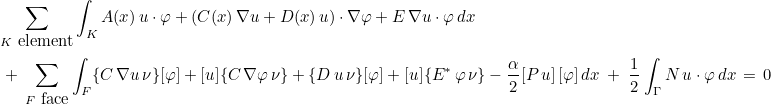
where ν is the normale outward from K- to K+, and we denote
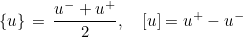
The tensor denoted P is a penalization matrix. For first-order problems (C = 0), if you set :
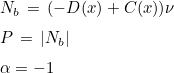
Then the obtained LDG formulation is the classical one with upwind fluxes. You can also choose simpler forms of P, for example :
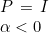
The specification of matrix P is done in methods GetPenalDG and MltPenalDG. When second-order formulation is chosen, matrix N will be equal to 0, and the boundary condition will be set will the same method as for continuous finite elements (through a DtN operator). When first-order formulation is set, the matrix N will contain the boundary condition operator. On each face of the boundary, u- is known and used in fluxes, while for u+, we are replacing the term :
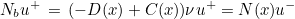
As a result, you have to exploit boundary conditions to express Nb u+ as a function of u-. Matrix N is given through methods MltNabc and GetNabc. Finally, we show the header of a class implementing the solution of a first-order problem with Discontinuous Galerkin method:
//! inheritance from GenericEquation
class MyNewEquation
: public GenericEquation<Complex_wp>
{
public :
enum{nb_unknowns = 2, nb_components_en = 1, nb_components_hn = 1, nb_unknowns_scal = 2, nb_unknowns_vec = 4};
static const bool FirstOrderFormulation = true;
static inline bool SymmetricGlobalMatrix() { return false; }
static inline bool SymmetricElementaryMatrix() { return false; }
// computation of V = A*U
template<class TypeEquation, class T0, class Vector1, class Vector2>
static void ApplyTensorMass(const EllipticProblem<TypeEquation>& var, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat, int ref, Vector1& U, Vector2& V);
// computation of V = E*dU
template<class TypeEquation, class T0, class Vector1, class Vector2>
static void ApplyGradientUnknown(const EllipticProblem<TypeEquation>& var, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat, int ref, Vector1& dU, Vector2& V);
// computation of dV = D*U
template<class TypeEquation, class T0, class Vector1, class Vector2>
static void ApplyGradientFctTest(const EllipticProblem<TypeEquation>& var, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat, int ref, Vector1& U, Vector2& dV);
// providing A in mass
template<class TypeEquation, class T0, class Matrix1>
static void GetTensorMass(const EllipticProblem<TypeEquation>& vars,
int i, int j, const GlobalGenericMatrix<T0>& nat_mat, int ref, Matrix1& mass);
// providing D and E in Dgrad_phi and Ephi_grad
template<class TypeEquation, classs T0, class MatStiff<
static void GetGradPhiTensor(const EllipticProblem<TypeEquation>& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat, int ref, MatStiff& Dgrad_phi, MatStiff& Ephi_grad);
// providing N in Nabc
template<class Matrix1, class GenericPb, class T0>
static void GetNabc(Matrix1& Nabc, const typename Dimension::R_N& normale,
int ref, int iquad, int k, const GlobalGenericMatrix<T0>& nat_mat, int ref_d,
const GenericPb& vars, const ElementReference<Dimension, 1>& Fb);
// computation of Un = N*Vn
template<class Vector1, class TypeEquation, class T0>
static void MltNabc(typename Dimension::R_N& normale, int ref,
const Vector1& Vn, Vector1& Un, int num_elem1, int k,
const GlobalGenericMatrix<T0>& nat_mat, int ref_d,
const EllipticProblem<TypeEquation>& vars, const ElementReference<Dimension, 1>& Fb);
// providing P in Nabc
templatel<class Matrix1, class GenericPb, class T0>
static void GetPenalDG(Matrix1& Nabc, const typename Dimension::R_N& normale,
int iquad, int k, const GlobalGenericMatrix<T0>& nat_mat, int ref,
const GenericPb& vars, const ElementReference<Dimension, >& Fb);
// computation of Un = P*Vn
template<class Vector1, class Vector2, class GenericPb, class T0>
static void MltPenalDG(const typename Dimension::R_N& normale, const Vector1& Vn, Vector2& Un,
int i, int k, const GlobalGenericMatrix<T0>& nat_mat, int ref,
const GenericPb& vars, const ElementReference<Dimension, 1>& Fb);
};
General formulation used for edge elements
Edge elements are used to approximate H(curl) finite element space. In Montjoie, they are only applied to Maxwell's equations (and variants). As a result, the variational formulation considered is quite simple
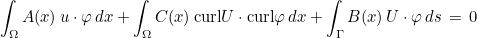
The associated pde is equal to :
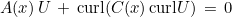
Boundary condition is set with a DtN operator (denoted B(x) here). If you want to see how to implement tensors A(x) and C(x), you can look at classes HarmonicMaxwellEquation_2D and HarmonicMaxwellEquation_3D.
ComputeDFjm1
Syntax
| static bool ComputeDFjm1() |
This method returns true if the jacobian matrices DFi will be computed and inverted. The inverse of jacobian matrices is needed to compute the gradient of basis functions. Unless, you have your own computation of elementary matrices (by using other variables), it is advised to not overload this method for your equation. The default values is true (returned by the class GenericEquation).
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
inline static bool ComputeDFjm1() { return false;}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
SymmetricGlobalMatrix
Syntax
| static bool SymmetricGlobalMatrix() |
This method returns true if the finite element matrix is symmetric. The default values is false (returned by the class GenericEquation). If you are sure that the finite element matrix obtained with the variational formulation is symmetric, you can overload this method to specify it. It will induce a gain of computation time and storage, since direct solvers exploit this property.
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
inline static bool SymmetricGlobalMatrix() { return true;}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
SymmetricElementaryMatrix
Syntax
| static bool SymmetricElementaryMatrix() |
This method returns true if the elementary finite element matrix is symmetric. The default values is false (returned by the class GenericEquation). If you are sure that the elementary finite element matrix obtained with the variational formulation is symmetric, you can overload this method to specify it. The elementary matrix involves only volume integrals (surface integrals are not included).
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
inline static bool SymmetricElementaryMatrix() { return true;}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
GetOtherElementType
Syntax
| static IVect GetOtherElementType() |
This method returns the list of finite element types for other mesh numberings. In Montjoie, we consider that there is a main mesh numbering (for most of equations, the degrees of freedom will be counted with this main mesh numbering. For some equations, other mesh numberings are needed. For the main mesh numbering the type of finite element is stored in the attribute type_element. It is equal to 1 for scalar finite elements, 2 for edge elements and 3 for facet elements. For other mesh numberings, the type of finite element is returned by the method GetOtherElementType.
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
// for instance H(div) space for the main unknown, H^1 and H(curl) space are needed for other unknowns
enum { type_element = 3};
inline static IVect GetOtherElementType() { IVect type(2); type(0) = 1; type(1) = 2; return type;}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
ComputeMassMatrix
Syntax
| static void ComputeMassMatrix(EllipticProblem& var, int i, const ElementReference_Dim& Fb) |
This method is aimed to compute quantities needed for the computation of elementary matrices. It can be interesting to precompute some quantities such that the computation of elementary matrices is faster. An example can be seen in the file src/Elliptic/Helmholtz/VarHelmholtz.cxx. Most of the time, this method does not need to be overloaded (empty method in the class GenericEquation).
Parameters
- var (inout)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- Fb (in)
- finite element object
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
GetTensorMass
Syntax
| static void GetTensorMass(const EllipticProblem& var, int i, int j, const GlobalGenericMatrix& nat_mat, int ref, Matrix&A) |
This method fills the tensor A (as introduced in the general formulation) for a given quadrature point of the mesh. This method will be called if you call the generic function ComputeElementaryMatrix to compute the elementary matrix of your equation.
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref (in)
- reference of the physical domain
- A (out)
- tensor A
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
// for instance if you want to solve
// -i omega rho u + dv/dx + dv/dy + \Delta u = 0
// u - i omega mu v + dv/dy - du/dx + d^2 v / dx^2 = 0
// mass tensor is equal to ([-i omega, 0], [1, - i omega])
template<class TypeEquation, class T0, class MatMass>
static void GetTensorMass(const EllipticProblem<TypeEquation<& vars,
int i, int j, const GlobalGenericMatrix<T0>& nat_mat,
int ref, MatMass& mass)
{
// mass does not need to be allocated (since it is a TinyMatrix
// assuming that rho and mu are stored in vars
Complex_wp m_iomega; vars.GetMiomega(m_iomega);
mass.Zero();
mass(0, 0) = m_iomega * vars.ref_rho(ref);
mass(1, 0) = 1.0;
mass(1, 1) = m_iomega * vars.ref_mu(ref);
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
ApplyTensorMass
Syntax
| static void ApplyTensorMass(const EllipticProblem& var, int i, int j, const GlobalGenericMatrix& nat_mat, int ref, const Vector&U, Vector&V) |
This method computes the product of the tensor A (as introduced in the general formulation) with a vector U for a given quadrature point of the mesh. This method will be called if you call the generic method MltAddFree to compute the matrix-vector product with the finite element matrix.
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref (in)
- reference of the physical domain
- U (in)
- input vector
- V (out)
- result V = A U
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
// for instance if you want to solve
// -i omega rho u + dv/dx + dv/dy + \Delta u = 0
// u - i omega mu v + dv/dy - du/dx + d^2 v / dx^2 = 0
// mass tensor is equal to ([-i omega, 0], [1, - i omega])
template<class TypeEquation, class T0, class MatMass>
static void GetTensorMass(const EllipticProblem<TypeEquation<& vars,
int i, int j, const GlobalGenericMatrix<T0>& nat_mat,
int ref, MatMass& mass)
{
// mass does not need to be allocated (since it is a TinyMatrix
// assuming that rho and mu are stored in vars
Complex_wp m_iomega; vars.GetMiomega(m_iomega);
mass.Zero();
mass(0, 0) = m_iomega * vars.ref_rho(ref);
mass(1, 0) = 1.0;
mass(1, 1) = m_iomega * vars.ref_mu(ref);
}
template<class TypeEquation, class T0, class Vector1>
static void ApplyTensorMass(const EllipticProblem<TypeEquation<& vars,
int i, int j, const GlobalGenericMatrix<T0>& nat_mat,
int ref, const Vector1& U, Vector1& V)
{
Complex_wp m_iomega; vars.GetMiomega(m_iomega);
// we compute V = A U
V(0) = m_iomega * vars.ref_rho(ref) * U(0);
V(1) = U(0) + m_iomega * vars.ref_mu(ref)*U(1);
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
GetNeededDerivative
Syntax
| static void GetNeededDerivative(const EllipticProblem& var, const GlobalGenericMatrix& nat_mat, Vector& unknown_to_derive, Vector& fct_test_to_derive) |
This method fills vectors unknown_to_derive and fct_test_to_derive. If unknown_to_derive(i) is true, it means that the gradient of unknown i is needed (in the variational formulation). If fct_test_to_derive(i) is true, it means that the gradient of the test function associated with unknown i is needed. This method will be called if you call the generic method MltAddFree to compute the matrix-vector product with the finite element matrix (and avoid unnecessary computation if some gradients are not needed).
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- nat_mat (in)
- mass, damping and stiffness coefficients
- unknown_to_derive (out)
- list of unknowns that need an evaluation of the gradient
- fct_test_to_derive (out)
- list of test functions that need an evaluation of the gradient
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
template<class TypeEquation, class T0, class Vector1>
static void GetNeededDerivative(const EllipticProblem<TypeEquation<& vars,
const GlobalGenericMatrix<T0>& nat_mat,
Vector1& unknown_to_derive, Vector1& fct_test_to_derive)
{
unknown_to_derive.Fill(true);
fct_test_to_derive.Fill(true);
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
GetGradGradTensor
Syntax
| static void GetGradGradTensor(const EllipticProblem& var, int i, int j, const GlobalGenericMatrix& nat_mat, int ref, Matrix&Cgrad) |
This method fills the tensor C (as introduced in the general formulation) for a given quadrature point of the mesh. This method will be called if you call the generic method ComputeElementaryMatrix to compute the elementary matrix of your equation. The term added to the finite element matrix is the following one :
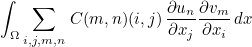
where un is the n-th component of the unknown U, and vm m-th component of the test-function V.
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref (in)
- reference of the physical domain
- Cgrad (out)
- tensor C evaluated at the quadrature point
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
template<class TypeEquation, class T0, class MatStiff>
static void GetGradGradTensor(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, MatStiff& Cgrad)
{
// for a laplacian (one unknown) :
Cgrad(0, 0)(0, 0) = nat_mat.GetCoefStiffness();
Cgrad(0, 0)(1, 1) = nat_mat.GetCoefStiffness();
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
ApplyTensorStiffness
Syntax
| static void ApplyTensorStiffness(const EllipticProblem& var, int i, int j, const GlobalGenericMatrix& nat_mat, int ref, const Matrix&U, Matrix&V) |
This method computes the result V = C U (where C is the tensor as introduced in the general formulation) for a given quadrature point of the mesh. This method will be called if you call the generic method MltAddFree to compute the matrix-vector product with the finite element matrix. The resulting matrix V is the following one :
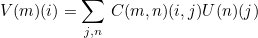
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref (in)
- reference of the physical domain
- U (in)
- input matrix U
- V (out)
- resulting matrix V
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
template<class TypeEquation, class T0, class MatStiff>
static void GetGradGradTensor(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, MatStiff& Cgrad)
{
// for a laplacian (one unknown) :
Cgrad(0, 0)(0, 0) = nat_mat.GetCoefStiffness();
Cgrad(0, 0)(1, 1) = nat_mat.GetCoefStiffness();
}
template<class TypeEquation, class T0, class Vector1>
static void ApplyTensorStiffness(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, const Vector1& U, Vector1& V)
{
V(0)(0) = nat_mat.GetCoefStiffness()*U(0)(0);
V(0)(1) = nat_mat.GetCoefStiffness()*U(0)(1);
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
GetGradPhiTensor
Syntax
| static void GetGradPhiTensor(const EllipticProblem& var, int i, int j, const GlobalGenericMatrix& nat_mat, int ref, Matrix&D, Matrix&E) |
This method fills the tensors D and E (as introduced in the general formulation) for a given quadrature point of the mesh. This method will be called if you call the generic method ComputeElementaryMatrix to compute the elementary matrix of your equation. The term added to the finite element matrix is the following one :
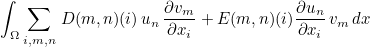
where un is the n-th component of the unknown U, and vm m-th component of the test-function V.
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref (in)
- reference of the physical domain
- D (out)
- tensor D evaluated at the quadrature point
- E (out)
- tensor E evaluated at the quadrature point
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
// for instance if you have the variational formulation
// -i omega \int rho u phi - v dphi/dx - v dphi/dy + du/dx dphi/dx + du/dy dphi/dy = 0
// u - i omega \int mu v psi - v dpsi/dy - du/dx psi - d v / dx dpsi/dx = 0
template<class TypeEquation, class T0, class MatStiff>
static void GetGradPhiTensor(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, MatStiff& D, MatStiff& E)
{
D(0, 1)(0) = -1.0; D(0, 1)(1) = -1.0;
D(1, 1)(1) = -1.0;
E(1, 0)(0) = -1.0;
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
ApplyGradientUnknown
Syntax
| static void ApplyGradientUnknown(const EllipticProblem& var, int i, int j, const GlobalGenericMatrix& nat_mat, int ref, const Matrix&U, Vector&V) |
This method computes the result V = E U (where E is the tensor as introduced in the general formulation) for a given quadrature point of the mesh. This method will be called if you call the generic method MltAddFree to compute the matrix-vector product with the finite element matrix. The resulting vector V is the following one :
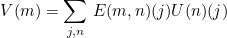
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref (in)
- reference of the physical domain
- U (in)
- input matrix U
- V (out)
- resulting vector V
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
// for instance if you have the variational formulation
// -i omega \int rho u phi - v dphi/dx - v dphi/dy + du/dx dphi/dx + du/dy dphi/dy = 0
// u - i omega \int mu v psi - v dpsi/dy - du/dx psi - d v / dx dpsi/dx = 0
template<class TypeEquation, class T0, class MatStiff>
static void GetGradPhiTensor(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, MatStiff& D, MatStiff& E)
{
D(0, 1)(0) = -1.0; D(0, 1)(1) = -1.0;
D(1, 1)(1) = -1.0;
E(1, 0)(0) = -1.0;
}
template<class TypeEquation, class T0, class MatStiff, class Vector1>
static void ApplyGradientUnknown(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, const MatStiff& U, Vector1& V)
{
V(1) = -U(0)(0);
}
template<class TypeEquation, class T0, class MatStiff, class Vector1>
static void ApplyGradientFctTest(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, const MatStiff& U, Vector1& V)
{
V(0)(0) = -U(1); V(0)(1) = -U(1);
V(1)(1) = -U(1);
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
ApplyGradientFctTest
Syntax
| static void ApplyGradientFctTest(const EllipticProblem& var, int i, int j, const GlobalGenericMatrix& nat_mat, int ref, const Vector&U, Matrix&V) |
This method computes the result V = D U (where D is the tensor as introduced in the general formulation) for a given quadrature point of the mesh. This method will be called if you call the generic method MltAddFree to compute the matrix-vector product with the finite element matrix. The resulting vector V is the following one :
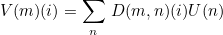
Parameters
- var (in)
- considered time-harmonic (or steady) problem
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref (in)
- reference of the physical domain
- U (in)
- input vector U
- V (out)
- resulting matrix V
Example :
class MyEquation : public GenericEquation<Complex_wp>
{
public :
// for instance if you have the variational formulation
// -i omega \int rho u phi - v dphi/dx - v dphi/dy + du/dx dphi/dx + du/dy dphi/dy = 0
// u - i omega \int mu v psi - v dpsi/dy - du/dx psi - d v / dx dpsi/dx = 0
template<class TypeEquation, class T0, class MatStiff>
static void GetGradPhiTensor(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, MatStiff& D, MatStiff& E)
{
D(0, 1)(0) = -1.0; D(0, 1)(1) = -1.0;
D(1, 1)(1) = -1.0;
E(1, 0)(0) = -1.0;
}
template<class TypeEquation, class T0, class MatStiff, class Vector1>
static void ApplyGradientUnknown(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, const MatStiff& U, Vector1& V)
{
V(1) = -U(0)(0);
}
template<class TypeEquation, class T0, class MatStiff, class Vector1>
static void ApplyGradientFctTest(const EllipticProblem<TypeEquation<& vars, int i, int j,
const GlobalGenericMatrix<T0>& nat_mat,
int ref, const MatStiff& U, Vector1& V)
{
V(0)(0) = -U(1); V(0)(1) = -U(1);
V(1)(1) = -U(1);
}
};
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
GetNabc
Syntax
| static void GetNabc( | Matrix& Nabc, const R_N& normale, int ref, int i, int j, const GlobalGenericMatrix& nat_mat, |
| int ref_d, const EllipticProblem& var, const ElementReference_Dim& Fb) |
This method fills the tensor N appearing in Discontinuous Galerkin formulations to treat boundary conditions. This method will be called if you call the generic function AddElementaryFluxesDG to compute the numerical fluxes of your equation. The term added to the finite element matrix is the following one :
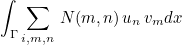
where un is the n-th component of the unknown U, and vm m-th component of the test-function V.
Parameters
- Nabc (out)
- tensor N evaluated at the quadrature point
- normale (in)
- outgoing normale
- ref (in)
- reference of the surface
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref_d (in)
- reference of the physical domain
- var (in)
- considered time-harmonic (or steady) problem
- Fb (in)
- finite element
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
MltNabc
Syntax
| static void MltNabc( | const R_N& normale, int ref, const Vector& u, Vector& v, int i, int j, const GlobalGenericMatrix& nat_mat, |
| int ref_d, const EllipticProblem& var, const ElementReference_Dim& Fb) |
This method computes the product v = N u where N is the tensor appearing in Discontinuous Galerkin formulations to treat boundary conditions.
Parameters
- normale (in)
- outgoing normale
- ref (in)
- reference of the surface
- u (in)
- input vector
- v (in)
- resulting vector v = N u
- i (in)
- element number
- j (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref_d (in)
- reference of the physical domain
- var (in)
- considered time-harmonic (or steady) problem
- Fb (in)
- finite element
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
GetPenalDG
Syntax
| static void GetPenalDG( | Matrix& P, const R_N& normale, int i, int j, int num_face, const GlobalGenericMatrix& nat_mat, |
| int ref_d, int ref_d2, const EllipticProblem& var, const ElementReference_Dim& Fb) |
This method fills the tensor P appearing in Discontinuous Galerkin formulations (Penality terms). This method will be called if you call the generic function AddElementaryFluxesDG to compute the numerical fluxes of your equation. The term added to the finite element matrix is the following one :
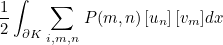
where un is the n-th component of the unknown U, and vm m-th component of the test-function V.
Parameters
- P (out)
- tensor P evaluated at the quadrature point
- normale (in)
- outgoing normale
- i (in)
- element number
- j (in)
- quadrature point number
- num_face (in)
- face number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref_d (in)
- reference of the physical domain
- ref_d2 (in)
- reference of the physical domain on adjacent element
- var (in)
- considered time-harmonic (or steady) problem
- Fb (in)
- finite element
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx
MltPenalDG
Syntax
| static void MltPenalDG( | const R_N& normale, const Vector& u, Vector& v, int i, int j, int num_face, const GlobalGenericMatrix& nat_mat, |
| int ref_d, int ref_d2, const EllipticProblem& var, const ElementReference_Dim& Fb) |
This method computes the product v = P u where P is the tensor appearing in Discontinuous Galerkin formulations to treat penalty terms.
Parameters
- normale (in)
- outgoing normale
- u (in)
- input vector
- v (in)
- resulting vector v = N u
- i (in)
- element number
- j (in)
- quadrature point number
- num_face (in)
- face number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref_d (in)
- reference of the physical domain
- ref_d2 (in)
- reference of the physical domain of the adjacent element
- var (in)
- considered time-harmonic (or steady) problem
- Fb (in)
- finite element
Location :
Harmonic/GenericEquation.hxx
Harmonic/GenericEquationInline.cxx