Time schemes
Several time schemes have been implemented, we distinguish explicit time-schemes from implicit time-schemes. You can use the implementation of time schemes provided by Montjoie for your own evolution problem. The model problem is the first-order evolution problem :
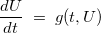
An example of use of time schemes for this equation is detailed below
class MyFunction
{
public :
void EvaluateFunction(const Real_wp& t, VectReal_wp& u, VectReal_wp& gU)
{
// you fill g(t, U) in vector gU
gU(0) = u(1);
gU(1) = -u(0);
}
};
// instance of MyFunction
MyFunction sys;
// for example we consider Runge-Kutta explicit scheme
RungeKutta_Iterator<Real_wp> RK;
// initialization of coefficients by giving the order
RK.SetOrder(4);
// initialization of the scheme by providing the first iterate and time step
Real_wp t0 = 0, dt = 0.01;
VectReal_wp U0(N);
U0.Fill(0);
RK.SetInitialCondition(t0, dt, U0, sys);
// then loop in times
for (int nt = 0; nt < nb_max_iterations; nt++)
{
// computation of U^n+1
// the result is present in RK.Y
RK.Advance(t, nt, sys);
}
// you can release memory used by the time scheme (intermediary vectors)
RK.Clear();
Time schemes for first-order evolution systems
| RungeKutta_Iterator | explicit Runge-Kutta schemes |
| Talezer_Iterator | explicit Tal-ezer schemes |
| AdamsBashforth_Moulton_Iterator | explicit Adams-Bashforth-Moulton schemes |
| TaylorSeries_Iterator | explicit scheme based on Taylor expansion |
| LowStorageRK_Iterator | explicit low-storage Runge-Kutta schemes |
| MultiStepButcher_Iterator | explicit multistep Butcher's schemes |
| OptimalModifiedEquation_Iterator | optimal modified equation schemes |
| SdirkScheme_Iterator | Singly-diagonally implicit Runge-Kutta schemes |
| SdirkScheme_Iterator | Singly-diagonally implicit Runge-Kutta schemes |
| LocalImperialeScheme_Iterator | local-time stepping with optimal modified equation approach (Imperiale's scheme) |
| LocalPipernoScheme_Iterator | local-time stepping with symplectic approach (Piperno's scheme) |
| ModifiedEquationSystemIterator | modified equation approach |
Time schemes for second-order evolution systems
| TetaScheme_Iterator | implicit theta-scheme |
| ModifiedEquationIterator | modified equation approach |
Functions related to unsteady simulations
| RunTimeScheme | completes time simulation of a first-order evolution system |
| RunFirstOrderScheme | completes time simulation of a first-order evolution system |
| RunSecondOrderScheme | completes time simulation of a second-order evolution system |
| ExtractSubMesh | extraction of a small mesh for the computation of the local time step |
| EvaluateCFL | evaluation of the global CFL number |
| ComputeLocalTimeStep | computation of the local CFL for each element of the mesh |
Functions related to unsteady simulations
| RunTimeScheme | completes time simulation of a first-order evolution system |
Public methods of VarInstationary
| GetNbDof | returns the size of the evolution system |
| GetNormeSolution | returns the L2 norm of the solution |
| WriteSnapshot | writes outputs (if needed) at a given time |
| FirstOrderScheme | returns true if the evolution system involves only first-order derivatives |
| ImplicitScheme | returns true if the selected scheme is implicit |
| SetTimeScheme | sets the time scheme to use |
| InitTimeIterations | initialisation beforing running time iterations |
| GetCflScheme | returns the coefficient involved in stability condition of the selected time scheme |
| ComputeStiffnessMatrix | computes stiffness matrix |
| ComputeMassMatrix | computes mass and damping matrix |
| GiveLevelTime | initialization of time levels for local time-stepping |
| SetLevel | sets level (which part of stiffness matrix will be involved) |
| GetNumberOfUnknowns | computes and returns the size of the evolution system |
| GetNbScalarUnknowns | returns the number of degrees of freedom for the scalar unknown |
| GetNbVectorialUnknowns | returns the number of degrees of freedom for the vectorial unknown |
| GetNbVectorialUnknownsPML | returns the number of degrees of freedom for the vectorial unknown and for PML elements |
| RunTimeIterations | runs time iterations |
| RunAll | runs complete simulation (from reading input file until writing snapshots at regular time intervals) |
| EvaluateFunction | evaluation of g(t,U) in the evolution system du/dt = g(t, U) |
| EvaluateDerivativeFunction | evaluation of time derivatives of g(t,U) in the evolution system du/dt = g(t, U) |
| ApplyOperatorKh | multiplication by stiffness matrix |
| ApplyOperatorDh | multiplication by scalar mass matrix |
| ApplyOperatorSh | multiplication by scalar damping matrix |
| ApplyOperatorShVectorial | multiplication by vectorial damping matrix |
| ApplyOperatorDhMinusdtSh | multiplication by matrix Dh - Δ t/2 Sh |
| SolveOperatorDhPlusdtSh | resolution by matrix Dh + Δ t/2 Sh |
| SolveOperatorDh | resolution by scalar mass matrix |
| SolveCholeskyDh | resolution of system L x = y or LT x = y where Dh = L LT |
| SolveOperatorDhPlusGammaKh | resolution by matrix Dh + γ Kh |
| ApplyOperatorRhScalar | multiplication by scalar stiffness matrix |
| ApplyOperatorRhVectorial | multiplication by vectorial stiffness matrix |
| ApplyOperatorBhMinusdtSh | multiplication by matrix Bh - Δ t/2 Sh |
| SolveOperatorBhPlusdtSh | resolution by matrix Bh + Δ t/2 Sh |
| SolveOperatorBh | resolution by vectorial mass matrix |
| SolveMassMatrix | resolution by mass matrix |
| Assemble | assembles global vector (for parallel computations) |
| SetInitialVector | computation of the initial condition |
| GiveIterate | method called in RunTimeScheme to provide an iterate |
| GiveVectorialIterate | method called in RunFirstOrderScheme to provide the vectorial iterate |
| GiveFinalIterate | method called in RunTimeScheme to provide the final iterate |
| GiveNumberIterations | method called in RunTimeScheme to provide the number of iterations |