Boundary conditions in Montjoie
The boundary conditions implemented in Montjoie are listed in the class BoundaryConditionEnum :
- LINE_DIRICHLET : Dirichlet condition
- LINE_NEUMANN : Neumann condition
- LINE_ABSORBING : absorbing boundary condition
- LINE_HIGH_CONDUCTIVITY : equivalent boundary condition for a highly conducting object
- LINE_IMPEDANCE : Robin boundary condition
- LINE_THIN_SLOT : equivalent boundary condition for a thin slot
- LINE_NEIGHBOR : this boundary is at the interface between two processors
- LINE_TRANSMISSION : transmission boundary conditions
- LINE_DTN : Dirichlet-to-Neumann operator
- LINE_SUPPORTED : Dirichlet condition concerning only some components of u
The boundary conditions are usually taken into account in the finite element matrix (through the variational formulation). Dirichlet and Supported boundary conditions are set by setting the concerned rows and columns to 0, with 1 on the diagonal. For inhomogenous Dirichlet, the columns are kept before erasing them so that the right hand side is modified. Periodic boundary conditions can be set by changing the numbers of degrees of freedom. Quasi-periodic boundary conditions are set either in the variational formulation or by modifying some rows of the finite element matrix.
The treatment of usual boundary conditions is performed in the class VarBoundaryCondition which is a base class of EllipticProblem.
Public attributes of VarBoundaryCondition
| NewColumnNumbers_Impedance | new column numbers when adding the surface integrals against basis functions |
| ProcColumnNumbers_Impedance | processor numbers (for columns) when adding the surface integrals against basis functions |
| NewRowNumbers_Impedance | new row numbers when adding the surface integrals against basis functions |
| ProcRowNumbers_Impedance | processor numbers (for rows) when adding the surface integrals against basis functions |
| take_into_account_curvature_for_abc | if true, the curvature is taken into account for absorbing boundary condition |
| grazing_abc | if true, the absorbing boundary condition is changed to handle mainly grazing waves |
| gamma_cla_coef | Parameter of the absorbing absorbing condition (for Helmholtz only) |
| theta_cla_coef | Parameter of the absorbing absorbing condition (for Helmholtz only) |
| zeta_cla_coef | Parameter of the absorbing absorbing condition (for Helmholtz only) |
Methods of VarBoundaryCondition
| GetInitialSymmetrization | returns true if the matrix can be symmetrized |
| GetBoundaryConditionId | returns the integer representing the boundary condition |
| GetNbDirichletDof | returns the number of dofs associated with Dirichlet condition |
| GetNbGlobalDirichletDof | returns the total number of dofs associated with Dirichlet condition (for all processors) |
| GetDirichletDofNumber | returns the dof number of the i-th dof associated with Dirichlet condition |
| IsDofDirichlet | returns true if the dof i is associated with a Dirichlet condition |
| GetIsDofDirichlet | returns the array containing informations about Dirichlet dofs |
| UseSymmetricDirichlet | returns true if rows and columns associated with Dirichlet dofs are removed |
| EnableSymmetricDirichlet | informs that rows and columns associated with Dirichlet dofs will be removed |
| GetCoefficientDirichlet | returns the coefficient used on the diagonal for Dirichlet dofs |
| SetCoefficientDirichlet | sets the coefficient used on the diagonal for Dirichlet dofs |
| SetDirichletDof | sets a degree of freedom as Dirichlet |
| GetNbSupportedComponents | returns the number of components to set to 0 for supported boundary condition |
| GetSupportedComponent | returns the component number of the i-th component to set to 0 for supported boundary condition |
| SetSupportedComponents | sets the component numbers for supported boundary condition |
| ImposeNullDirichletCondition | sets to 0 values associated with Dirichlet condition |
| GetHighConductivityOrder | returns the order for high-conductivity boundary condition |
| FindDofsOnReference | finds all the dofs associated with a reference (or a list of references) |
| TreatDirichletCondition | finds all the dofs associated with Dirichlet condition |
| SetDirichletDofs | provides a list of Dirichlet dofs |
| ResizeNbDof | changes the number of degrees of freedom of the problem |
| ComputeDirichletCoef | provides a coefficient that can be used for the diagonal for Dirichlet dofs |
| ApplyDirichletCondition | modification of the right hand side when inhomogeneous Dirichlet condition is specified |
| UpdateDirichletDofs | updates arrays for Dirichlet dofs after calls to SetDirichletDof |
| GetNbModes | returns the number of modes for computations on periodized meshes or cyclic meshes |
| GetNbModesSource | returns the number of modes for the computation of sources |
| GetModeNumber | returns the mode number of mode i |
| GetCurrentModeNumber | returns the mode number of the current solved mode |
| SetCurrentModeNumber | sets the mode number of the current solved mode |
| ModesNotStored | returns true if the modes are not stored (prevents from the use of fft but requires less memory) |
| ForceStorageModes | enables/disables the storage of modes |
| GetSymmetryType | returns the type of periodicity/symmetry for the computation of the solution (periodic in x, y, z and/or theta) |
| GetNbPeriodicDof | returns the number of degrees of freedom involved in periodic boundary conditions |
| GetPeriodicDof | returns the i-th periodic dof number |
| GetOriginalPeriodicDof | returns the corresponding number of the i-th periodic dof number |
| GetProcOriginalPeriodicDof | returns the corresponding number of the i-th periodic dof number |
| GetFormulationForPeriodicCondition | returns the formulation used to handle periodic boundary conditions |
| SetModesToCompute | sets the list of modes to be computed |
| PushBackMode | adds a mode at the end of the list of modes |
| GetNbPeriodicModesX | returns the number of modes (for x-periodicity) |
| GetNbPeriodicModesY | returns the number of modes (for y-periodicity) |
| GetNbPeriodicModesZ | returns the number of modes (for z-periodicity) |
| GetPeriodicNumberModes | retrieves the number of modes in x, y, z |
| GetPeriodicModes | retrieves the mode number (in x, y, z) from its global number |
| SetPeriodicCondition | modifies the finite element matrix to enforce periodic conditions |
| ApplyPeriodicCondition | modifies the right hand side because of periodic conditions |
| GetOrderAbsorbingCondition | returns the order of approximation for the absorbing boundary condition |
| GetNbEltPML | returns the number of elements contained in PML layers |
| GetNbGlobalEltPML | returns the global number of elements contained in PML layers (for all processors) |
| MltMuIntegrationByParts | multiplies a coefficient by mu (physical coefficient) |
| SetPhysicalIndexAtInfinity | updates the physical indexes at infinity |
| GetMaximumVelocityPML | returns the maximal velocity in PMLs |
| FindElementsInsidePML | finds elements that are contained in PMLs |
| EvaluateFunctionTauPML | evaluates the damping function of PML layers |
| GetDampingFactorPML | evaluates the damping factor of PML layers |
| GetDampingTauPML | evaluates the damping function of PML layers |
| AddMatrixImpedanceBoundary | adds to a given matrix surface integrals against basis functions |
| AddBoundaryConditionTerms | adds to the finite element matrix the terms due to boundary conditions |
| InitCyclicDomain | initializes the computation of modes for cyclic or periodic domains |
| ComputeQuasiPeriodicPhase | computes the phase for quasi-periodic conditions |
| AllocateTauPML | allocates arrays storing damping coefficients for PMLs |
| GetPeriodicDofNumbers | retrieves the dof numbers for periodic conditions |
| GetPeriodicPhase | retrieves the phase for quasi-periodic condition |
| GetParamCondition | gets parameters of a boundary condition |
| MltParamCondition | multiplies a coefficient by parameters of a boundary condition |
| GetImpedanceCoefficientABC | returns the coefficient to modify absorbing boundary condition |
| GetTauPML | returns the damping function of PMLs on a quadrature point |
| GetPrimitiveTauPML | returns the primitive of the damping function of PMLs on a quadrature point |
| SetBoundaryConditionMesh | sets a boundary condition for a given reference |
| AddPeriodicConditionMesh | links two references with a periodic condition |
| GetNewImpedanceABC | returns an object computing the impedance coefficient for absorbing boundary conditions |
| GetNewImpedanceGeneric | returns an object computing the impedance coefficient for Robin boundary conditions |
| GetNewImpedanceHighConductivity | returns an object computing the impedance coefficient for high conductivity boundary conditions |
Methods for ImpedanceFunction_Base
The class ImpedanceFunction_Base is the base class for all impedance classes (such as ImpedanceGeneric, ImpedanceABC or ImpedanceHighConductivity). These classes are used for impedance boundary conditions when the function AddMatrixImpedanceBoundary is called to add the corresponding terms to the finite element matrix.
| InvolveOnlyTangentialDofs | returns true if only tangential dofs (associated with the surface) are involved in surface integrals |
| SetCoefficient | sets the impedance coefficients (in the case of an uniform impedance) |
| GetCoefficient | returns the impedance coefficient at a given quadrature point |
| PresenceGradient | returns true if the boundary integrals involve the gradient of basis functions |
| EvaluateImpedancePhi | evaluates the impedance involved in surface integrals against basis functions |
| EvaluateImpedanceGrad | evaluates the impedance involved in surface integrals against gradient of basis functions |
| ApplyImpedancePhi_H1 | applies the impedance involved in surface integrals against scalar basis functions |
| ApplyImpedanceGrad | applies the impedance involved in surface integrals against gradient of scalar basis functions |
| ApplyImpedancePhi_Hcurl | applies the impedance involved in surface integrals against basis functions (edge elements) |
| ApplyImpedanceCurl | applies the impedance involved in surface integrals against the curl of basis functions (edge elements) |
| ApplyImpedancePhi_Hdiv | applies the impedance involved in surface integrals against basis functions (facet elements) |
| ApplyImpedanceDiv | applies the impedance involved in surface integrals against the divergence of basis functions (facet elements) |
Transparent conditions
The details of transparent conditions is detailed in the thesis of M. Duruflé. The cornerstone of this method is a representation integral of the field outside a surface. In the case of Maxwell's equations, these formulas (known as Stratton-Chu formulas) are equal to
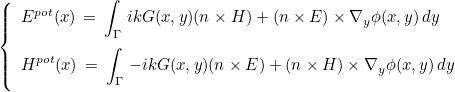
with the Green kernel and dyadic Green function :
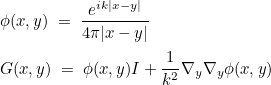
There are similar expression for Helmholtz equation. Transparent conditions are not implemented with other equations. Γ is an intermediary surface surrounding the scatterer and Σ the external boundary. The boundary condition is then set on Σ to :
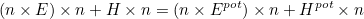
The linear system to solve is then equal to
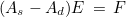
The matrix As is the finite element matrix with a first-order absorbing boundary condition (this matrix is sparse) whereas the matrix Ad is the matrix containing the integral equation terms (this matrix has an important dense block). The matrix As is factorized (or solved iteratively), and the transparent condition is solved iteratively on the following linear system
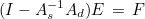
If the distance between Γ and Σ is large enough (one wavelength is fine), the number of iterations needed to solve this system is quite small. The treatment of transparent conditions is handled by the class TransparencySolver.
Public methods of TransparencySolver
| constructor of TransparencySolver | |
| UseTransparentCondition | returns true if a transparent condition is set |
| Solve | solves the linear system associated with the transparent condition |
| Init | initialisation and computation of arrays needed for the resolution of the linear system associated with the transparent condition |
| ComputeSolution | computes the solution of As x = y |
| ComputeGreenKernel | computation of Green kernel and dyadic Green function |
| ComputeSurfaceGammaAndAbsorbing | computes the quadrature points on the two surfaces |
| ComputeRightHandSide | computes the matrix-vector product Ad x |
| ComputeAndStoreEnPot | computes the integral representation of E x n (and H x n) on all quadrature points |
| GetSource | computes the source term (on a given quadrature point) for the transparent condition |
| ComputeIntegralRepresentation | computes the integral representation of E x n (and H x n) on a given point |
For Helmholtz and Maxwell's equations, it is also possible to compute the far field (through an integral over a surface). The computation of the far field (also known as radar cross section) is performed in class VarComputationRCS
Public methods of VarComputationRCS
| RcsToBeComputed | returns true if a radar cross section needs to be computed |
| GetNbAngles | returns the number of angles for which we want to know the far field |
| GetNbPointsOutside | returns the number of points for which we want to know the field |
| GetInterpolationMesh | returns the surface mesh used for the computation of the RCS |
| GetRcsType | returns the type of radar cross section (monostatic or bistatic) |
| GetOutsidePoint | returns the coordinates of the points where we want to know the field |
| SetOutsidePoints | sets the coordinates of the points where we want to know the field |
| SetTimeStep | sets the time step (for unsteady equations) |
| InitComputationRCS | initializes the object before computing RCS |
| ComputeIntegralRepresentation | computes the value of the field outside the computational domain with an integral representation |
| ComputeRCS | effective computation of the radar cross section |
Dirichlet Boundary condition (LINE_DIRICHLET)
Dirichlet boundary conditions can be homogeneous
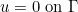
or inhomogeneous
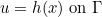
In the case of edge elements, Dirichlet condition is actually a perfectly conductor condition :
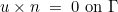
Dirichlet condition is set by setting to 0 the concerned rows and columns and putting 1 on the diagonal. This coefficient one can be changed for the computation of eigenvalues to avoid the pollution of the spectrum with eigenvalues equal to 1. For discontinuous Galerkin formulations, the Dirichlet condition is handled in the variational formulation.
Neumann boundary conditions are equal for the Laplace and Helmholtz equation
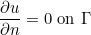
In the case of Maxwell's equations, it refers to :
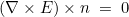
In the case of elastodynamics, it refers to :
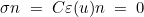
In the case of aeroacoustics, it refers to :
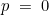
As you can see, this boundary condition depends on the considered equation, but usually is associated with the boundary condition that will cancel the boundary integral coming from the integration by parts.
Supported Boundary condition (LINE_SUPPORTED)
Supported boundary conditions consists of imposing a Dirichlet condition
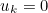
for only a subset of components k of the unknown u. The components are given after the word SUPPORTED, for instance ConditionReference = 1 2 SUPPORTED 0 3 in the datafile. For other components, a natural condition is imposed (no boundary terms like for Neumann condition).
Dirichlet to Neumann (LINE_DTN)
This condition is reserved for a future implementation of Dirichlet-to-Neumann operators in Montjoie
Transmission conditions (LINE_TRANSMISSION)
Transmission conditions are present for some models in Montjoie. The documentation will be updated later.
False boundary condition (LINE_NEIGHBOR)
LINE_NEIGHBOR is used for boundaries located at the interface between two processor. For such boundaries, no boundary condition is needed. However in Montjoie, since the face is isolated (no adjacent face in the current processor), a boundary condition is needed. That's why, such faces are affected with this false boundary condition.
Thin-slot models (LINE_THIN_SLOT)
Thin slot models are implemented in Montjoie for 2-D Helmholtz equation. The documentation will be updated later.
High-conductivity models (LINE_HIGH_CONDUCTIVITY)
High-conductivity models are implemented in Montjoie for Helmholtz and Maxwell's equations. The documentation will be updated later.
Robin boundary conditions (LINE_IMPEDANCE)
Robin boundary conditions consists of considering.
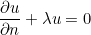
for scalar equations. The documentation will be updated later.
Absorbing boundary conditions (LINE_ABSORBING)
Absorbing boundary conditions are used to truncate the computational domain. For most of equations, only first-order absorbing boundary conditions are implemented. For Helmholtz equations, it consists of considering.
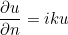
where k is the wave number.
NewColumnNumbers_Impedance, ProcColumnNumbers_Impedance
This attribute is an array used when adding boundary terms in the finite element matrix. You can modify the column numbers of the degrees of freedom such that the term.
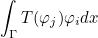
is added to the entry i, NewColumnNumbers_Impedance(j) of the matrix (instead of i, j). ProcColumnNumbers_Impedance is used in parallel to store the processor associated with the new number. If the processor is equal to the current processor, the column number is local, whereas it is global for a different processor.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// initializing an empty matrix;
int N = var.GetNbDof();
DistributedMatrix<Real_wp, General, ArrayRowSparse> A;
A.Reallocate(N, N);
// filling the new column numbers (here we place random numbers)
var.NewColumnNumbers_Impedance.Reallocate(N);
var.NewColumnNumbers_Impedance.FillRand();
// for parallel computation you can also set a different processor number
var.ProcColumnNumbers_Impedance.Reallocate(N);
var.ProcColumnNumbers_Impedance.Fill(0);
// then you can add the impedance term
GlobalGenericMatrix<Real_wp> nat_mat;
IVect ref(var.mesh.GetNbReferences()+1); ref.Zero(); ref(3) = 1;
var.AddMatrixImpedanceBoundary(1.0, ref, 1, nat_mat, A, 0, 0, imped, true, false, var);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
NewRowNumbers_Impedance, ProcRowNumbers_Impedance
This attribute is an array used when adding boundary terms in the finite element matrix. You can modify the row numbers of the degrees of freedom such that the term.
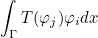
is added to the entry NewRowNumbers_Impedance(i), j of the matrix (instead of i, j). ProcRowNumbers_Impedance is used in parallel to store the processor associated with the new number. If the processor is equal to the current processor, the row number is local, whereas it is global for a different processor.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// initializing an empty matrix;
int N = var.GetNbDof();
DistributedMatrix<Real_wp, General, ArrayRowSparse> A;
A.Reallocate(N, N);
// filling the new row numbers (here we place random numbers)
var.NewRowNumbers_Impedance.Reallocate(N);
var.NewRowNumbers_Impedance.FillRand();
// for parallel computation you can also set a different processor number
var.ProcRowNumbers_Impedance.Reallocate(N);
var.ProcRowNumbers_Impedance.Fill(0);
// then you can add the impedance term
GlobalGenericMatrix<Real_wp> nat_mat;
IVect ref(var.mesh.GetNbReferences()+1); ref.Zero(); ref(3) = 1;
var.AddMatrixImpedanceBoundary(1.0, ref, 1, nat_mat, A, 0, 0, imped, false, true, var);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
take_into_account_curvature_for_abc
This attribute is a boolean. If it is set to true, the absorbing boundary condition will include the term due to the curvature (1/R term). This feature is only implemented for Helmholtz equation. It is usually modified by inserting a line ModifiedImpedance = CURVE in the data file.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
grazing_abc
This attribute is a boolean. If it is set to true, the absorbing boundary condition will be modified to handle correctly grazing waves. This feature is only implemented for Helmholtz equation. It is usually modified by inserting a line OrderAbsorbingBoundaryCondition = 1 GRAZING in the data file.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
gamma_cla_coef, theta_cla_coef, zeta_cla_coef
These attributes are doubles that are used to parametrize absorbing boundary conditions. This feature is only implemented for Helmholtz equation. It is usually modified by inserting a line OrderAbsorbingBoundaryCondition = 2 PARAMETERS 0.2 0.5 1.0 in the data file.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
GetInitialSymmetrization
This method returns true if the matrix (for a mixed formulation) can be symmetrized (with respect to boundary conditions). It does not mean that the matrix will be symmetrized when PerformFactorizationStep is called.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// the matrix can be symmetrized ?
bool init_sym = var.GetInitialSymmetrization();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
GetBoundaryConditionId
Syntax
| int GetBoundaryConditionId(IVect ref, int pos, VectString parameters, bool& periodic) |
This method returns the integer corresponding to the boundary condition given as a string (or a list of strings). Usually, only parameters(pos) is used to determine the boundary condition. For more complex boundary conditions, several parameters can be used (parameters(pos), parameters(pos+1), etc). The first argument is not used, the last argument is true if the boundary condition corresponds to a periodic (or quasi-periodic condition).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// boundary condition id (e.g. BoundaryConditionEnum::LINE_DIRICHLET) ?
IVect ref; int pos = 1; VectString parameters(pos+1);
parameters(pos) = "DIRICHLET"; bool periodic;
int id = var.GetBoundaryConditionId(ref, pos, parameters, periodic);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
GetNbDirichletDof
Syntax
| int GetNbDirichletDof() const |
This method returns the number of degrees of freedom associated with a Dirichlet condition (u = f). Only degrees of freedom of the current processor are counted.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of Dirichlet dofs for the current processor
nb_dir_dof = var.GetNbDirichletDof();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbGlobalDirichletDof
Syntax
| int GetNbGlobalDirichletDof() const |
This method returns the number of degrees of freedom associated with a Dirichlet condition (u = f). Degrees of freedom of all the processors are counted.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of Dirichlet dofs for the overall simulation (with all processors)
nb_dir_dof = var.GetNbGlobalDirichletDof();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetDirichletDofNumber
Syntax
| int GetDirichletDofNumber(int i ) const |
| const IVect& GetDirichletDofNumber() const |
This method returns the dof number of the i-th Dirichlet dof. In the second syntax, you can retrieve the array containing Dirichlet dofs.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of Dirichlet dofs for the current processor
nb_dir_dof = var.GetNbGlobalDirichletDof();
// loop over Dirichlet dofs
for (int i = 0; i < nb_dir_dof; i++)
{
// you can retrieve a single dof
int num_dof = var.GetDirichetDofNumber(i);
}
// or all the dofs
const IVect& dir_dof = var.GetDirichletDofNumber();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
IsDofDirichlet
Syntax
| bool IsDofDirichlet(int i ) const |
This method returns true if the degree of freedom i is associated with a Dirichlet condition (u = f).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// dof 32 is Dirichlet ?
bool dof_dir = var.IsDofDirichlet(32);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetIsDofDirichlet
Syntax
| const Vector<bool>& GetIsDofDirichlet() const |
This method returns the array containing booleans to know if a degree of freedom is Dirichlet or not.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// dof 32 is Dirichlet ?
bool dof_dir = var.IsDofDirichlet(32);
// if you want all the values at once
const VectBool& arr_dir = var.GetIsDofDirichlet();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
UseSymmetricDirichlet
Syntax
| bool UseSymmetricDirichlet() const |
This method returns true if rows and columns associated with Dirichlet dofs are removed (and a non-null coefficient is put on the diagonal). This treatment is already performed for symmetric matrices. If the method returns true, the treatment will also be performed for unsymmetric matrices. If the method returns false, only rows are erased for unsymmetric matrices.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// rows and columns are eliminated for Dirichlet ?
bool dir_sym = var.UseSymmetricDirichlet();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
EnableSymmetricDirichlet
Syntax
| bool EnableSymmetricDirichlet(bool sym = true) const |
If the argument sym is true, rows and columns associated with Dirichlet dofs are removed (and a non-null coefficient is put on the diagonal). This treatment is already performed for symmetric matrices, but will be also performed for unsymmetric matrices. The aim is to obtain a better conditioning of the finite element matrix. This feature is usually activated by inserting a line ForceDirichletSymmetry = YES in the datafile.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if we want to eliminate rows and columns for Dirichlet dofs
var.EnableSymmetricDirichlet();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetCoefficientDirichlet
Syntax
| Real_wp GetCoefficientDirichlet() const |
This method returns the coefficient set on the diagonal for Dirichlet dofs. Rows associated with Dirichlet dofs are removed, only a coefficient is kept on the diagonal.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// coefficient on diagonal for Dirichlet ?
Real_wp coef = var.GetCoefficientDirichlet();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
SetCoefficientDirichlet
Syntax
| void SetCoefficientDirichlet(Real_wp coef) const |
This method sets the coefficient set on the diagonal for Dirichlet dofs. Rows associated with Dirichlet dofs are removed, only a coefficient is kept on the diagonal. You can also modify this coefficient (initially equal to one) by inserting a line DirichletCoefMatrix = 2.0 in the datafile.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// modifying coefficient on diagonal for Dirichlet
var.SetCoefficientDirichlet(Real_wp(2));
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
SetDirichletDof
Syntax
| void SetDirichletDof(int n, bool b) const |
This method sets the n-th degree of freedom as a Dirichlet dof (if b is true). Once you have manually modified Dirichlet dofs, you need to call the method UpdateDirichletDofs to reconstruct the array storing the Dirichlet dofs.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// manually adding Dirichlet dofs (not recommended)
var.SetDirichletDof(3, true);
var.SetDirichletDof(12, true);
// you can also remove Dirichlet dofs
var.SetDirichletDof(11, false);
// once you finished, you call UpdateDirichletDofs
var.UpdateDirichletDofs();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbSupportedComponents
Syntax
| int GetNbSupportedComponents(int ref) const |
This method returns the number of components for the supported boundary condition for the considered reference.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of components for reference 1 ?
int nb_comp = var.GetNbSupportedComponents(1);
// loop over supported components
for (int k = 0; k < nb_comp; k++)
{
// displaying the list of components for the supported boundary condition for reference 1
cout << "component " << var.GetSupportedComponent(1, k) << endl;
}
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetSupportedComponent
Syntax
| int GetSupportedComponent(int ref , int k ) const |
This method returns a component number for the supported boundary condition. The supported boundary condition consists of imposing
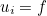
for integers i that corresponds to component numbers.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of components for reference 1 ?
int nb_comp = var.GetNbSupportedComponents(1);
// loop over supported components
for (int k = 0; k < nb_comp; k++)
{
int i = var.GetSupportedComponent(1, k);
// displaying the list of components for the supported boundary condition
cout << "component " << i << endl;
// we have u_i = f
}
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
SetSupportedComponents
Syntax
| void SetSupportedComponents(int ref , IVect num ) const |
This method sets the list of component numbers for the supported boundary condition. The supported boundary condition consists of imposing
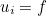
for integers i that corresponds to component numbers. Usually the components of the supported boundary condition are set in the data file.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// setting manually components for the supported boundary condition for reference 2
IVect num(2); num(0) = 2; num(1) = 5; int ref = 2;
var.SetSupportedComponents(ref, num);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
ImposeNullDirichletCondition
Syntax
| void ImposeNullDirichletCondition(Vector& u) const |
This method enforces an homogeneous Dirichlet condition
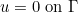
for the input vector u.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
VectReal_wp u(var.GetNbDof()); u.FillRand();
// setting u = 0 for Dirichlet dofs
var.ImposeNullDirichletCondition(u);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetHighConductivityOrder
Syntax
| int GetHighConductivityOrder() const |
This method returns the order of approximation for the high-conductivity boundary condition.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// order for high-conductivity boundary condition
int r_conduc = var.GetHighConductivityOrder();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
FindDofsOnReference
Syntax
| void FindDofsOnReference(const VarProblem& var, const IVect& ref_cond, int ref_target, IVect& Dofs) const |
This method retrieves the degrees of freedom associated with faces (edges in 2-D) such that the reference ref satisfies ref_cond(ref) = ref_target.
Parameters
- var (in)
- instance of VarProblem
- ref_cond (in)
- references i such that ref_cond(i) = ref_target are considered
- ref_target (in)
- target reference
- Dofs (out)
- list of degrees of freedom located on the selected referenced faces
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// degrees of freedom for reference 2 and 3 ?
IVect ref_cond(var.mesh.GetNbReferences()+1); ref_cond.Zero();
int ref_target = 1; ref_cond(2) = ref_target; ref_cond(3) = ref_target;
IVect Dofs;
var.FindDofsOnReference(var, ref_cond, ref_target, Dofs);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
TreatDirichletCondition
Syntax
| void TreatDirichletCondition() |
This method computes all the degrees of freedom located on Dirichlet boundaries. This method does not need to be called in a regular use, since it is already called by ComputeMeshAndFiniteElement.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
SetDirichletDofs
Syntax
| void SetDirichletDofs(int N, IVect dof_list) |
This method sets all the degrees of freedom considered as Dirichlet dofs (i.e. such that the equation u = f is imposed on these dofs). Previous Dirichlet dofs are removed and replaced by the provided list. After calling this method, you do not need to call UpdatedirichletDofs.
Parameters
- N (in)
- number of Dirichlet dofs
- dof_list (in)
- dof numbers
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// degrees of freedom for reference 2 and 3 ?
IVect ref_cond(var.mesh.GetNbReferences()+1); ref_cond.Zero();
int ref_target = 1; ref_cond(2) = ref_target; ref_cond(3) = ref_target;
IVect Dofs;
var.FindDofsOnReference(var, ref_cond, ref_target, Dofs);
// then you can choose to impose Dirichlet on these dofs (and remove previous Dirichlet dofs)
var.SetDirichletDofs(Dofs.GetM(), Dofs);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ResizeNbDof
Syntax
| void ResizeNbDof(int N) |
This method changes the number of degrees of freedom of the global problem. It is better to call that method other SetNbDof since IsDofDirichlet will work correctly.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// you want to add a new degree of freedom
int N = var.GetNbDof();
var.ResizeNbDof(N+1);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ComputeDirichletCoef
Syntax
| void ComputeDirichletCoef(VirtualMatrix& A) |
This method evaluates the largest eigenvalue of the input matrix A (by iterative power method) and returns twice this estimation. This value can then be used as Dirichlet coefficient (on the diagonal), such that eigenvalues due to Dirichlet condition will be outside the spectrum of interest.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// computing the matrix
GlobalGenericMatrix<Real_wp> nat_mat;
DistributedMatrix<Real_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixWithBC(A, nat_mat);
// coefficient for Dirichlet diagonal ?
Real_wp coef = var.ComputeDirichletCoef(A);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
UpdateDirichletDofs
Syntax
| void UpdateDirichletDofs() |
This method updates the arrays for Dirichlet dofs. It has to be called if Dirichlet dofs have been set manually with SetDirichletDof.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// manually adding Dirichlet dofs (not recommended)
var.SetDirichletDof(3, true);
var.SetDirichletDof(12, true);
// you can also remove Dirichlet dofs
var.SetDirichletDof(11, false);
// once you finished, you call UpdateDirichletDofs
var.UpdateDirichletDofs();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyDirichletCondition
Syntax
| void ApplyDirichletCondition(SeldonTranspose trans , FemMatrixFreeClass& , A, Vector& b , int k = 0) const |
This method modifies the right hand side because of inhomogeneous Dirichlet condition. To recover the symmetry of the matrix, rows and columns associated with Dirichlet dofs are removed. As a result, the right hand side must be modified to take into account inhomogeneous Dirichlet condition (u = f). On input, the right hand side b contains values of f on degrees of freedom. This method does not need to be called in a regular use, since ComputeSolution already calls it.
Parameters
- trans (in)
- Do we want to solve A x = b or the transpose system ?
- A (in)
- iterative finite element matrix
- b (inout)
- right hand side to modify
- k (optional)
- right hand side number
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetNbModes
Syntax
| int GetNbModes() const |
This method returns the number of modes to compute in order to recover the solution for a source that has no symmetry (only the computational domain has symmetry). For example, in case of cyclic domains, it is the number of Fourier modes. If the computational domain has no symmetry, it returns one.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of modes to compute the solution (for periodic/cyclic domains)
nb_modes = var.GetNbModes();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbModesSource
Syntax
| int GetNbModesSource() const |
This method returns the number of modes to compute in order to recover the solution for a source that has no symmetry (only the computational domain has symmetry). For example, in case of cyclic domains, it is the number of Fourier modes. If the computational domain has no symmetry, it returns one. The difference between GetNbModes and GetNbModesSource happens for axisymmetric computation. In that case, each mode is solved independently, and there is only "one mode" for the computation of the source, since we compute directly the decomposition of the source on the required mode.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of modes for the evaluation of the source
nb_modes = var.GetNbModesSource();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetModeNumber
Syntax
| int GetModeNumber(int i ) const |
This method returns the mode number of the i-th mode to compute. For instance, if we consider axisymmetric computations, where the solution is written as
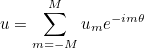
If all the modes (between -M and M) are involved, the first computed mode will be m=0, then m=1, then m=-1, etc. So the method GetModeNumber will return -1 for i = 2.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of modes for the evaluation of the source
nb_modes = var.GetNbModesSource();
// first mode to be computed
int m = var.GetModeNumber(0);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetCurrentModeNumber
Syntax
| int GetCurrentModeNumber() const |
This method returns the mode number of the current mode that is solved.
Example :
EllipticProblem<HelmholtzEquationAxi> var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// setting a mode number (value of m)
var.SetCurrentModeNumber(1);
// then you can retrieve this number
int m = var.GetCurrentModeNumber();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
SetCurrentModeNumber
Syntax
| void SetCurrentModeNumber(int m ) const |
This method sets the mode number of the current mode that will be solved.
Example :
EllipticProblem<HelmholtzEquationAxi> var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// setting a mode number (value of m)
var.SetCurrentModeNumber(1);
// then you can retrieve this number
int m = var.GetCurrentModeNumber();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
ModesNotStored
Syntax
| bool ModesNotStored() const |
This method returns true if the modes are not stored. When the modes are not stored, the final solution is modified at each computation. If the modes are stored, fft can be used to obtain quickly the final solution. This functionality is turned on/off by inserting a line StorageModes = YES in the data file.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// modes will be stored ?
bool store_modes = var.ModesNotStored();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
ForceStorageModes
Syntax
| bool ForceStorageModes(bool store = true) |
This method enables (or disables) the storage of modes. When the modes are not stored, the final solution is modified at each computation. If the modes are stored, fft can be used to obtain quickly the final solution. This functionality is usually turned on/off by inserting a line StorageModes = YES in the data file.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to force the storage of modes
var.ForceStorageModes(true);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetSymmetryType
Syntax
| int GetSymmetryType() |
This method returns the type of symmetry that will be used for the computation of the solution. It can be equal to
- NO_SYMMETRY : no symmetry is present (default case) : only one mode is computed
- PERIODIC_THETA : cyclic domain (only a section is meshed)
- PERIODIC_X : periodic domain in x (only a cell is meshed)
- PERIODIC_Y : periodic domain in y (only a cell is meshed)
- PERIODIC_Z : periodic domain in z (only a cell is meshed)
- PERIODIC_XY : periodic domain in x and y (only a cell is meshed)
- PERIODIC_XZ : periodic domain in x and z(only a cell is meshed)
- PERIODIC_YZ : periodic domain in y and z (only a cell is meshed)
- PERIODIC_XYZ : periodic domain in x, y and z (only a cell is meshed)
- PERIODIC_ZTHETA : periodic domain in z and theta (only a cell is meshed)
The periodic conditions are set when inserting a line ConditionReference = 1 2 CYCLIC in the data file.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// type of periodicity in the mesh ?
int sym = var.GetSymmetryType();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbPeriodicDof
Syntax
| int GetNbPeriodicDof() |
This method returns the number of degrees of freedom that are labelled periodic. For these degrees of freedom, the following equation
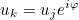
replaces the variational formulation. This replacement is performed only for a strong formulation of quasi-periodic conditions (UseSameDofsForPeriodicCondition = NO in the data file).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of dofs where quasi-periodic condition is applied
int nb_dof_per = var.GetNbPeriodicDof();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetPeriodicDof
Syntax
| int GetPeriodicDof(int i) |
This method returns the number k of the i-th periodic dof. For these degrees of freedom, the following equation
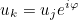
replaces the variational formulation. This replacement is performed only for a strong formulation of quasi-periodic conditions (UseSameDofsForPeriodicCondition = NO in the data file).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of dofs where quasi-periodic condition is applied
int nb_dof_per = var.GetNbPeriodicDof();
// loop over periodic dofs
for (int i = 0; i < nb_dof_per; i++)
{
// number of the periodic dof
int k = var.GetPeriodicDof(i);
// number of the original dof
int j = var.GetOriginalPeriodicDof(i);
// we have an equation u_k = u_j * e^{i phase}
}
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetOriginalPeriodicDof
Syntax
| int GetOriginalPeriodicDof(int i) |
This method returns the number j of the original degree of freedom associated with the i-th periodic dof. For periodic degrees of freedom, the following equation
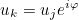
replaces the variational formulation. This replacement is performed only for a strong formulation of quasi-periodic conditions (UseSameDofsForPeriodicCondition = NO in the data file).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of dofs where quasi-periodic condition is applied
int nb_dof_per = var.GetNbPeriodicDof();
// loop over periodic dofs
for (int i = 0; i < nb_dof_per; i++)
{
// number of the periodic dof
int k = var.GetPeriodicDof(i);
// number of the original dof
int j = var.GetOriginalPeriodicDof(i);
// we have an equation u_k = u_j * e^{i phase}
}
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetProcOriginalPeriodicDof
Syntax
| int GetProcOriginalPeriodicDof(int i) |
This method returns the processor owning the original degree of freedom associated with the i-th periodic dof. For periodic degrees of freedom, the following equation
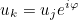
replaces the variational formulation. This replacement is performed only for a strong formulation of quasi-periodic conditions (UseSameDofsForPeriodicCondition = NO in the data file).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of dofs where quasi-periodic condition is applied
int nb_dof_per = var.GetNbPeriodicDof();
// loop over periodic dofs
for (int i = 0; i < nb_dof_per; i++)
{
// number of the periodic dof
int k = var.GetPeriodicDof(i);
// number of the original dof
int j = var.GetOriginalPeriodicDof(i);
// processor that owns this dof
int proc = var.GetProcOriginalPeriodicDof(i);
// we have an equation u_k = u_j * e^{i phase}
}
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetFormulationForPeriodicCondition
Syntax
| int GetFormulationForPeriodicCondition() |
This method returns the formulation used to handle quasi-periodic conditions. The method is chosen by inserting a line UseSameDofsForPeriodicCondition = NO in the data file. It can be equal to :
- SAME_PERIODIC_DOFS : the original and periodic dof have the same number. This formulation is perfect for periodic conditions, but quasi-periodic conditions cannot be handled.
- STRONG_PERIODIC : the original and periodic dof have different numbers, an equation uk = uj ei φ is imposed strongly.
- WEAK_PERIODIC : the quasi-periodic condition is enforced weakly (with surface integrals).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of dofs where quasi-periodic condition is applied
int nb_dof_per = var.GetNbPeriodicDof();
// formulation
int form = var.GetFormulationForPeriodicCondition();
// can be equal to MeshNumbering_Base<Real_wp>::STRONG_PERIODIC
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
SetModesToCompute
Syntax
| void SetModesToCompute(IVect num ) |
This method sets the list of modes that need to be solved for the computation of the solution.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// setting manually the list of modes
IVect num(2); num(0) = 1; num(1) = 3;
var.SetModesToCompute(num);
// GetModeNumber(0) will return 1
int m0 = var.GetModeNumber(0);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
PushBackMode
Syntax
| void PushBackMode(int n ) |
This method pushes a mode number at the end of the list of modes that need to be solved for the computation of the solution.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// setting manually the list of modes
IVect num(2); num(0) = 1; num(1) = 3;
var.SetModesToCompute(num);
// adding another mode
var.PushBackMode(5);
// GetModeNumber(2) will return 5
int m = var.GetModeNumber(2);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbPeriodicModesX
Syntax
| int GetNbPeriodicModesX() const |
This method returns the number of cells in x-direction (for periodicity in x).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of periodic modes in x-direction
int nx = var.GetNbPeriodicModesX();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbPeriodicModesY
Syntax
| int GetNbPeriodicModesY() const |
This method returns the number of cells in y-direction (for periodicity in y).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of periodic modes in y-direction
int ny = var.GetNbPeriodicModesY();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbPeriodicModesZ
Syntax
| int GetNbPeriodicModesZ() const |
This method returns the number of cells in z-direction (for periodicity in z).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of periodic modes in z-direction
int nz = var.GetNbPeriodicModesZ();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetPeriodicNumberModes
Syntax
| void GetPeriodicNumberModes(int& nx , int& ny , int& nz, bool& teta_sym ) const |
This method fills the number of modes in x, y and z-direction. It also sets teta_sym to true if there a cyclic boundary condition.
Parameters
- nx (out)
- number of modes in x-direction
- ny (out)
- number of modes in y-direction
- nz (out)
- number of modes in z-direction
- teta_sym (out)
- true if there is a cyclic computation
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of periodic modes in x, y and z-direction
int nx, ny, nz; bool teta_sym;
var.GetPeriodicNumberModes(nx, ny, nz, teta_sym);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetPeriodicModes
Syntax
| void GetPeriodicModes(int n , int& ix , int& iy , int& iz, bool& teta_sym ) const |
| void GetPeriodicModes(int n , Complex_wp& kx , Complex_wp& ky , Complex& kz) const |
This method fills the mode number in x, y and z-direction from the global mode number. It also sets teta_sym to true if there a cyclic boundary condition. In the second syntax, it sets the phase (in x, y and z). The phase in x is equal to
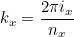
Parameters
- n (in)
- global mode number
- ix (out)
- mode number in x-direction
- iy (out)
- mode number in y-direction
- iz (out)
- mode number in z-direction
- teta_sym (out)
- true if there is a cyclic computation
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// for a given mode number
int n = 23;
// decomposition in x, y, and z
int ix, iy, iz;
var.GetPeriodicModes(n, ix, iy, iz, teta_sym);
// phase (2 pi / ix)
Complex_wp kx, ky, kz;
var.GetPeriodicModes(n, kx, ky, kz);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
SetPeriodicCondition
Syntax
| void SetPeriodicCondition(Matrix& A ) |
This method applies periodic (or quasi-periodic) conditions to a given matrix. This treatment is relevant only for a strong formulation of periodic boundary conditions, where equations
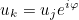
replaces the variational formulation for periodic degrees of freedom. In regular use, this method does not need to be called, since periodic boundary conditions are applied when AddMatrixWithBC is called.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyPeriodicCondition
Syntax
| void ApplyPeriodicCondition(Vector& x ) |
This method applies periodic (or quasi-periodic) conditions to the right hand side. This treatment is relevant only for a strong formulation of periodic boundary conditions, where equations
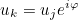
replaces the variational formulation for periodic degrees of freedom. In regular use, this method does not need to be called, since periodic boundary conditions are applied when ComputeSolution is called.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetOrderAbsorbingCondition
Syntax
| int GetOrderAbsorbingCondition() const |
This method returns the order of approximation for absorbing boundary conditions. For Helmholtz equations, it can be equal to 1 or 2. For other equations, only first-order absorbing boundary conditions are implemented.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// order for ABCs ?
int r_abc = var.GetOrderAbsorbingCondition();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbEltPML
Syntax
| int GetNbEltPML() const |
This method returns the number of elements inside the PMLs.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of elements in PMLs (for current processor)
int n_pml = var.GetNbEltPML();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetNbGlobalEltPML
Syntax
| int GetNbGlobalEltPML() const |
This method returns the global number of elements inside the PMLs. For a parallel computation, the method returns the sum of the number of elements (for all processors).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// number of elements in PMLs (for all processors)
int n_pml = var.GetNbGlobalEltPML();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
MltMuIntegrationByParts
Syntax
| void MltMuIntegrationByParts(int ref, int ne , int num_loc , int k, Real_wp& coef) const |
This method multiplies the coefficient by mu, which is a coefficient that appears in the boundary term when an integration by parts is performed. For instance, for Helmholtz equation, we have the term
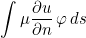
Parameters
- ref (in)
- reference of the physical domain
- ne (in)
- element number
- num_loc (in)
- local face number
- k (in)
- quadrature point number
- mu (inout)
- coefficient that will be multiplied by mu
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// for a given element
int ne = 14;
int ref = var.mesh.Element(ne).GetReference();
// local face of the element
int num_loc = 1, k = 14;
Real_wp coef(1);
// we want to compute coef = coef * mu
var.MltMuIntegrationByParts(ref, ne, num_loc, k, coef);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
GetMaximumVelocityPML
Syntax
| Real_wp GetMaximumVelocityPML() const |
This method returns the maximum velocity in PMLs.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// maximal velocity in PMLs ?
Real_wp vmax = var.GetMaximumVelocityPML();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
SetPhysicalIndexAtInfinity
Syntax
| void SetPhysicalIndexAtInfinity(const VectBool& RefUsed ) const |
This method computes the physical index (rho and mu for Helmholtz equation) at infinity. This method is already called by ComputeMeshAndFiniteElement and does not need to be called in regular use.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonicInline.cxx
FindElementsInsidePML
Syntax
| void FindElementsInsidePML() |
This method finds all the elements inside PMLs and marks them as PML elements. This method is already called by ComputeMeshAndFiniteElement and does not need to be called in regular use.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
EvaluateFunctionTauPML
Syntax
| void EvaluateFunctionTauPML(Real_wp dx , Real_wp sig , Real_wp a , Real_wp& zeta , Real_wp& zeta_p ) |
This method evaluates the damping function of the PML (usually a parabole).
Parameters
- dx (in)
- distance to the interface between the physical domain and PMLs
- sig (in)
- coefficient (damping is multiplied by this coefficient)
- a (in)
- thickness of the PML
- zeta (out)
- damping function
- zeta_p (out)
- primitive of zeta
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// damping function for a given distance ?
Real_wp zeta, zeta_p, thickness = 1.0;
var.EvaluateFunctionTauPML(dx, 1.0, thickness, zeta, zeta_p);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetDampingFactorPML
Syntax
| void GetDampingFactorPML(Mesh& mesh , int num_pml , int type_pml , R_N point , R_N& zeta , R_N& x_tilde ) |
This method evaluates the point after the complex variable change :
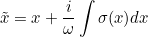
that appears in PML layers. It computes also, the coefficient
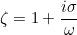
that appears for derivatives with respect to x (y or z). zeta is a vector because it contains this factor for each coordinate x, y (and z in 3-D).
Parameters
- mesh (in)
- input mesh
- num_pml (in)
- PML number
- type_pml (in)
- type of PML
- point (in)
- point where zeta is computed
- zeta (out)
- damping factor
- x_tilde (out)
- point after complex change variable
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// damping factor on a given point
int ne = 12;
int num_pml = var.Element(ne).GetNumberPML();
int type_pml = var.Element(ne).GetTypePML();
R2 point(0.8, 2.4);
R2_Complex_wp zeta, x_tilde;
var.GetDampingFactorPML(var.mesh, num_pml, type_pml, point, zeta, x_tilde);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetDampingTauPML
Syntax
| void GetDampingTauPML(Mesh& mesh , int num_pml , int type_pml , R_N point , R_N& tau , R_N& tau_p ) |
This method evaluates the damping coefficient of the PML (in the three coordinates) and its primitive.
Parameters
- mesh (in)
- input mesh
- num_pml (in)
- PML number
- type_pml (in)
- type of PML
- point (in)
- point where zeta is computed
- tau (out)
- damping coefficient
- tau_p (out)
- primitive of damping coefficient
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// damping factor on a given point
int ne = 12;
int num_pml = var.Element(ne).GetNumberPML();
int type_pml = var.Element(ne).GetTypePML();
R2 point(0.8, 2.4);
R2_Complex_wp tau, tau_p;
var.GetDampingTauPML(var.mesh, num_pml, type_pml, point, tau, tau_p);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
AddMatrixImpedanceBoundary
Syntax
| void AddMatrixImpedanceBoundary( | Real_wp alpha, IVect ref_cond , int ref_target , GlobalGenericMatrix nat_mat , |
| Matrix& mat_sp , int offset_row , int offset_col, ImpedanceFunction_Base& impedance, | |
| bool change_cols, bool change_rows, VarProblem& var) |
This method adds a boundary integral :
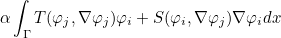
to a sparse matrix. The local operators T and S are defined through the object impedance. The surface Γ over which the integral is computed consists of the facs such that the reference ref satisfy ref_cond(ref) = ref_target.
Parameters
- alpha (in)
- coefficient
- ref_cond (in)
- Surface gamma is selected such that ref_cond(ref) = ref_target
- ref_target (in)
- reference target
- nat_mat (in)
- mass, damping and stiffness coefficients
- mat_sp (inout)
- sparse matrix that will be modified
- offset_row (in)
- offset for row numbers
- offset_col (in)
- offset for column numbers
- impedance (in)
- class defining impedance operators T and S
- change_cols (in)
- column numbers are modified with NewColumnNumbers_Impedance
- change_rows (in)
- rows numbers are modified with NewRowNumbers_Impedance
- var(in)
- instance of VarProblem
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// definition of impedance coefficients
ImpedanceFunction_Base<Real_wp, Dimension2> impedance;
impedance.SetCoefficient(Real_wp(2), Real_wp(-1)); // case of constant scalar impedance
// i.e. T(phi, \nabla phi) = coef phi, S(phi, \nabla phi) = coef \nabla phi P
// P is the tangential projector to take into account only surface gradient
// initializing a sparse matrix
DistributedMatrix<Real_wp, Symmetric, ArrayRowSymSparse> mat_sp;
int N = var.GetNbDof(); mat_sp.Reallocate(N, N);
// selecting the surfaces of integration
IVect ref_cond(var.mesh.GetNbReferences()+1); ref_cond.Zero();
int ref_target = 1; ref_cond(2) = ref_target;
// calling the method to add the integral terms to the matrix
GlobalGenericMatrix<Real_wp> nat_mat;
var.AddMatrixImpedanceBoundary(Real_wp(1), ref_cond, ref_target, nat_mat,
mat_sp, 0, 0, impedance, false, false, var);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
AddBoundaryConditionTerms
Syntax
| void AddBoundaryConditionTerms( | Matrix& A, GlobalGenericMatrix nat_mat , int offset_row = 0, int offset_col = 0) |
This method adds to the matrix the terms due to boundary conditions. On regular use, this method does not need to be called, since it is already called by AddMatrixWithBC.
Parameters
- A (inout)
- sparse matrix that will be modified
- nat_mat (in)
- mass, damping and stiffness coefficients
- offset_row (optional)
- offset for row numbers
- offset_col (optional)
- offset for column numbers
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
InitCyclicDomain
Syntax
| void InitCyclicDomain() |
This method initializes the computation of modes for cyclic or periodic domains. In regular use, this method does not need to be called since it is already called by ComputeMeshAndFiniteElement.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ComputeQuasiPeriodicPhase
Syntax
| void ComputeQuasiPeriodicPhase |
This method computes the phase for quasi-periodic conditions.
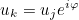
If you switch to another mode (for periodic/cyclic domains), this method needs to be called such that the quasi-periodic condition corresponds to the desired mode.
// The definition of the problem is constructed via EllipticProblem class
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE"); // name of the equation, it can be used to use an equivalent formulation of the same equation
ReadInputFile(input_file, var); // parameters of the ini file are read
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO"); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// once var is constructed, you can call AddMatrixWithBC
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to set coefficients alpha, beta and gamma
// By default, alpha = beta = gamma = 1
Matrix<Real_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixWithBC(A, nat_mat);
// but you can change them
Real_wp alpha = 2.0, beta = 0.5, gamma = 0.25;
nat_mat.SetCoefMass(alpha);
nat_mat.SetCoefDamping(beta);
nat_mat.SetCoefStiffness(gamma);
// matrix is added, so you need to clear it if you do not want to keep
// previous non-zero entries
A.Clear();
var.AddMatrixWithBC(A, nat_mat);
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Real_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
delete Ah;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
AllocateTauPML
Syntax
| void AllocateTauPML() |
This method allocates the arrays that will store damping terms for PMLs. In regular use, this method does not need to be called since it is already called by ComputeMassMatrix.
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetPeriodicDofNumbers
Syntax
| void GetPeriodicDofNumbers(int i , int& k , int& j , int n = 0) const |
This method retrieves the dofs numbers j, k of the periodic condition
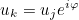
for the i-th periodic dof.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// loops over periodic dofs
for (int i = 0; i < var.GetNbPeriodicDof(); i++)
{
// integers j and k such that u_k = u_j * phase
int j, k;
var.GetPeriodicDofNumbers(i, k, j);
}
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetPeriodicPhase
Syntax
| void GetPeriodicPhase(int i , Complex_wp& phase ) const |
This method retrieves the phase for the quasi-periodic condition
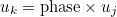
for the i-th periodic dof.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// loops over periodic dofs
for (int i = 0; i < var.GetNbPeriodicDof(); i++)
{
// integers j and k such that u_k = u_j * phase
int j, k;
var.GetPeriodicDofNumbers(i, k, j);
// phase
Complex_wp phase;
var.GetPeriodicPhase(i, phase);
}
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
MltParamCondition
Syntax
| void MltParamCondition(int ref, int k, T& coef) const |
This method multiplies a coefficient by the parameter given at a boundary condition.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// reference of the physical surface
int ref = 2;
// then if you want to retrieve parameter 1 associated with this reference
// for instance if the data file contains ConditionReference = 2 IMPEDANCE 4.0 2.5
// parameter 0 is 4.0 and parameter 1 is 2.5
Real_wp coef(1);
var.MltParamCondition(2, 1, coef);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetImpedanceCoefficientABC
Syntax
| Complexe GetImpedanceCoefficientABC() const |
This method returns the coefficient to modify the absorbing boundary condition. This coefficient is usually set by inserting a line ModifiedImpedance = 1.02 in the data file.
EllipticProblem<HelmholtzEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// coefficient to modify impedance for abc
Complex_wp coef = var.GetImpedanceCoefficientABC();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetTauPML
Syntax
| R_N GetTauPML(int num_elem , int k ) const |
| Complexe GetTauPML(int num_elem , int k , int num_coor ) const |
This method returns the value of the damping function for a quadrature point. This result is a vector because it contains the damping for each coordinate x, y (and z in 3-D). In the second syntax, we return the damping for a given coordinate.
Parameters
- num_elem (in)
- element number
- k (in)
- quadrature point number
- num_coor (in)
- coordinate number
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// damping function on a given point
R2 tau; int num_elem = 12, k = 2;
tau = var.GetTauPML(num_elem, k);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetPrimitiveTauPML
Syntax
| Complexe GetPrimitiveTauPML(int num_elem , int k , int num_coor ) const |
This method returns the value of the primitive of the damping function for a quadrature point.
Parameters
- num_elem (in)
- element number
- k (in)
- quadrature point number
- num_coor (in)
- coordinate number
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// damping function on a given point
Real_wp tau_y; int num_elem = 12, k = 2, num_coor = 1;
tau_y = var.GetTauPML(num_elem, k, num_coor);
// primitive as well :
Real_wp tau_yp = var.GetPrimitiveTauPML(num_elem, k, num_coor);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetParamCondition
Syntax
| Complexe GetParamCondition(int ref, int k) const |
| Vector<VectComplexe>& GetParamCondition() const |
This method retrieves a single parameter associated with a reference number. You can also retrieves all parameters for all references.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// reference of the physical surface
int ref = 2;
// then if you want to retrieve parameter 1 associated with this reference
// for instance if the data file contains ConditionReference = 2 IMPEDANCE 4.0 2.5
// parameter 0 is 4.0 and parameter 1 is 2.5
Real_wp coef = var.GetParamCondition(2, 1);
// if you want to get all parameters
Vector<VectReral_wp> >& all_param = var.GetParamCondition();
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
SetBoundaryConditionMesh
Syntax
| void SetBoundaryConditionMesh(int ref, int type) const |
This method sets a boundary condition for a given reference. Usually the boundary conditions are given by inserting a line ConditionReference = 1 DIRICHLET in the data file.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// if you want to set a boundary condition (not present in the data file)
var.SetBoundaryConditionMesh(1, BoundaryConditionEnum::LINE_NEUMANN);
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
AddPeriodicConditionMesh
Syntax
| void AddPeriodicConditionMesh(TinyVector<int, 2> ref, int type) const |
This method sets a periodic boundary condition between two references. Usually the boundary conditions are given by inserting a line ConditionReference = 1 2 PERIODICITY in the data file.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// if you want to set a periodic boundary condition (not present in the data file)
var.AddPeriodicConditionMesh(TinyVector<int, 2>(2, 3), BoundaryConditionEnum::PERIODIC_CTE);
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetNewImpedanceABC
Syntax
| ImpedanceFunction_Base* GetNewImpedanceABC(Complexe x) const |
This method constructs an impedance object for absorbing boundary conditions. The argument given as parameters is used to retrieve an object dealing complex or real numbers.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for absorbing boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceABC();
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetNewImpedanceGeneric
Syntax
| ImpedanceFunction_Base* GetNewImpedanceGeneric(Complexe x) const |
This method constructs an impedance object for absorbing boundary conditions. The argument given as parameters is used to retrieve an object dealing complex or real numbers.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for Robin boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceGeneric();
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetNewImpedanceHighConductivity
Syntax
| ImpedanceFunction_Base* GetNewImpedanceHighConductivity(Complexe x) const |
This method constructs an impedance object for high conductivity boundary conditions. The argument given as parameters is used to retrieve an object dealing complex or real numbers.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for high conductivity boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceHighConductivity();
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
InvolveOnlyTangentialDofs
Syntax
| bool InvolveOnlyTangentialDofs() const |
This method returns true if the boundary integrals are non-null only for degrees of freedom associated with the surface. Usually, it is the case. It can be false, for instance if the integral involves 3-D gradient of basis functions (and not surface gradients).
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for Robin boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceGeneric();
bool only_tgt_dofs = imped->InvolveOnlyTangentialDofs();
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
PresenceGradient
Syntax
| bool PresenceGradient() const |
This method returns true if the boundary integrals involve gradient (or curl/div) of basis functions. The aim is to save computational time when no gradients are needed.
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for Robin boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceGeneric();
bool presence_grad = imped->PresenceGradient();
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
SetCoefficient
Syntax
| bool SetCoefficient(Complexe a, Complexe b) |
This method sets the coefficients for the impedance. For scalar finite elements, these coefficients appear in the following term
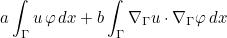
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for Robin boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceGeneric();
// setting coefficients a and b in the expression a \int_\Gamma u \varphi dx + b \int_\Gamma \nabla_\Gamma u \cdot \nabla_\Gamma \varphi \, dx
Real_wp a = 2.0, b = 3.0;
imped->SetCoefficient(a, b);
// initializing a sparse matrix
DistributedMatrix<Real_wp, Symmetric, ArrayRowSymSparse> mat_sp;
int N = var.GetNbDof(); mat_sp.Reallocate(N, N);
// selecting the surfaces of integration
IVect ref_cond(var.mesh.GetNbReferences()+1); ref_cond.Zero();
int ref_target = 1; ref_cond(2) = ref_target;
// calling the method to add the integral terms to the matrix
GlobalGenericMatrix<Real_wp> nat_mat;
var.AddMatrixImpedanceBoundary(Real_wp(1), ref_cond, ref_target, nat_mat,
mat_sp, 0, 0, *imped, false, false, var);
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
GetCoefficient
Syntax
| bool GetCoefficient( | int i, int num_elem, int num_loc, int k, int ref_domain, int ref |
| SetPoints pts, SetMatrices mat) |
This method returns the impedance coefficient at a given quadrature point.
Parameters
- i (in)
- face number
- num_elem (in)
- element number
- num_loc (in)
- local face number
- k (in)
- quadrature point number
- ref_domain (in)
- reference for the physical domain
- ref (in)
- reference for the surface
- pts (in)
- quadrature points
- mat (in)
- jacobian matrices
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for Robin boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceGeneric();
int i = 2; // edge number
int num_elem = var.mesh.BoundaryRef(i).numElement(0);
int num_loc = var.mesh.Element(num_elem).GetPositionBoundary(i);
int ref_domain = var.mesh.Element(num_elem).GetReference();
int ref = var.mesh.BoundaryRef(i).GetReference();
VectR2 s;
mesh.GetVerticesElement(num_elem, s);
const ElementReference_Dim<Dimension2>& Fb = var.GetReferenceElement(num_elem);
SetPoints<Dimension2> pts; SetMatrices<Dimension2> mat;
Fb.FjElemQuadrature(s, pts, mesh, num_elem);
Fb.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
Fb.FjSurfaceElem(s, pts, mesh, num_elem, num_loc);
Fb.DFjSurfaceElem(s, pts, mat, mesh, num_elem, num_loc);
// evaluation of impedance
int k = 2; // local quadrature point number
GlobalGenericMatrix<Real_wp> nat_mat;
imped->EvaluateImpedancePhi(i, num_elem, i, num_loc, k, nat_mat, ref_domain, pts, mat);
// then if you want to get the coefficient
Real_wp coef = imped->GetCoefficient(i, num_elem, num_loc, k, ref_domain, ref, pts, mat);
bool presence_grad = imped->PresenceGradient();
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
EvaluateImpedancePhi
Syntax
| void EvaluateImpedancePhi( | int i, int num_elem, int num_edge, int num_loc, int k, GlobalGenericMatrix nat_mat, int ref_domain, |
| SetPoints pts, SetMatrices mat) |
This method evaluates the impedance for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called, such that the user can compute impedance coefficients (or operators). Then, the method ApplyImpedancePhi_H1 is called to apply the impedance against basis functions.
Parameters
- i (in)
- face number
- num_elem (in)
- element number
- num_edge (in)
- equal to i
- num_loc (in)
- local face number
- k (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref_domain (in)
- reference for the physical domain
- pts (in)
- quadrature points
- mat (in)
- jacobian matrices
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for Robin boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceGeneric();
int i = 2; // edge number
int num_elem = var.mesh.BoundaryRef(i).numElement(0);
int num_loc = var.mesh.Element(num_elem).GetPositionBoundary(i);
int ref_domain = var.mesh.Element(num_elem).GetReference();
int ref = var.mesh.BoundaryRef(i).GetReference();
VectR2 s;
mesh.GetVerticesElement(num_elem, s);
const ElementReference_Dim<Dimension2>& Fb = var.GetReferenceElement(num_elem);
SetPoints<Dimension2> pts; SetMatrices<Dimension2> mat;
Fb.FjElemQuadrature(s, pts, mesh, num_elem);
Fb.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
Fb.FjSurfaceElem(s, pts, mesh, num_elem, num_loc);
Fb.DFjSurfaceElem(s, pts, mat, mesh, num_elem, num_loc);
// evaluation of impedance
int k = 2; // local quadrature point number
GlobalGenericMatrix<Real_wp> nat_mat;
imped->EvaluateImpedancePhi(i, num_elem, i, num_loc, k, nat_mat, ref_domain, pts, mat);
// then if you want to get the coefficient
Real_wp coef = imped->GetCoefficient(i, num_elem, num_loc, k, ref_domain, ref, pts, mat);
bool presence_grad = imped->PresenceGradient();
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
EvaluateImpedanceGrad
Syntax
| void EvaluateImpedanceGrad( | int i, int num_elem, int num_edge, int num_loc, int k, GlobalGenericMatrix nat_mat, int ref_domain, |
| SetPoints pts, SetMatrices mat) |
This method evaluates the impedance (for gradients) for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called, such that the user can compute impedance coefficients (or operators). Then, the method ApplyImpedanceGrad is called to apply the impedance against gradient of basis functions.
Parameters
- i (in)
- face number
- num_elem (in)
- element number
- num_edge (in)
- equal to i
- num_loc (in)
- local face number
- k (in)
- quadrature point number
- nat_mat (in)
- mass, damping and stiffness coefficients
- ref_domain (in)
- reference for the physical domain
- pts (in)
- quadrature points
- mat (in)
- jacobian matrices
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// impedance for Robin boundary condition
ImpedanceFunction_Base<Real_wp, Dimension2>* imped = var.GetNewImpedanceGeneric();
int i = 2; // edge number
int num_elem = var.mesh.BoundaryRef(i).numElement(0);
int num_loc = var.mesh.Element(num_elem).GetPositionBoundary(i);
int ref_domain = var.mesh.Element(num_elem).GetReference();
int ref = var.mesh.BoundaryRef(i).GetReference();
VectR2 s;
mesh.GetVerticesElement(num_elem, s);
const ElementReference_Dim<Dimension2>& Fb = var.GetReferenceElement(num_elem);
SetPoints<Dimension2> pts; SetMatrices<Dimension2> mat;
Fb.FjElemQuadrature(s, pts, mesh, num_elem);
Fb.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
Fb.FjSurfaceElem(s, pts, mesh, num_elem, num_loc);
Fb.DFjSurfaceElem(s, pts, mat, mesh, num_elem, num_loc);
// evaluation of impedance
int k = 2; // local quadrature point number
GlobalGenericMatrix<Real_wp> nat_mat;
imped->EvaluateImpedancePhi(i, num_elem, i, num_loc, k, nat_mat, ref_domain, pts, mat);
// then if you want to get the coefficient
Real_wp coef = imped->GetCoefficient(i, num_elem, num_loc, k, ref_domain, ref, pts, mat);
bool presence_grad = imped->PresenceGradient();
// for gradient
imped->EvaluateImpedanceGrad(i, num_elem, i, num_loc, k, nat_mat, ref_domain, pts, mat);
// once used, delete the object
delete imped;
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyImpedancePhi_H1
Syntax
| void ApplyImpedancePhi_H1( | int m, int k, int offset, TinyVector phi, R2 grad_phi, Vector f_phi) |
This method applies the impedance for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called for the computation of the boundary integral.
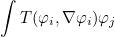
where T is the impedance operator, i the row index and j the column index. This method can be overloaded to define your own impedance operator. This method involves only scalar basis functions (unknown number m is approximated with H1 Sobolev space).
Parameters
- m (in)
- unknown number (for rows)
- j (in)
- quadrature point number
- offset (in)
- offset for the unknown m
- phi (in)
- value of basis function (row)
- grad_phi (in)
- gradient of basis function (row)
- f_phi (in)
- result vector T(phi, grad_phi)
// for your own impedance operator
class MyOperator : public ImpedanceFunction_Base<Real_wp, Dimension2>
{
void ApplyImpedancePhi_H1(int m, int j, int offset, const TinyVector<Real_wp, 1>& phi,
const R2& grad_phi, Vector<T>& f_phi)
{
// for a diagonal operator :
Real_wp coef = 4.5; // impedance coefficient
f_phi(offset) = coef*phi(0);
}
};
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyImpedanceGrad
Syntax
| void ApplyImpedanceGrad( | int m, int k, int offset, TinyVector phi, R2 grad_phi, Vector f_phi) |
This method applies the impedance for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called for the computation of the boundary integral.
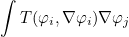
where T is the impedance operator, i the row index and j the column index. This method can be overloaded to define your own impedance operator. This method involves only scalar basis functions (unknown number m is approximated with H1 Sobolev space).
Parameters
- m (in)
- unknown number (for rows)
- j (in)
- quadrature point number
- offset (in)
- offset for the unknown m
- phi (in)
- value of basis function (row)
- grad_phi (in)
- gradient of basis function (row)
- f_phi (in)
- result vector T(phi, grad_phi)
// for your own impedance operator
class MyOperator : public ImpedanceFunction_Base<Real_wp, Dimension2>
{
void ApplyImpedancePhi_H1(int m, int j, int offset, const TinyVector<Real_wp, 1>& phi,
const R2& grad_phi, Vector<T>& f_phi)
{
// for a diagonal operator :
f_phi.Zero();
Real_wp coef = 4.5; // impedance coefficient
f_phi(offset) = coef*phi(0);
}
void ApplyImpedanceGrad(int m, int j, int offset, const TinyVector<Real_wp, 1>& phi,
const R2& grad_phi, Vector<T>& f_phi)
{
// if no gradient term, you can fill with zeros
f_phi.Zero();
}
};
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyImpedancePhi_Hcurl
Syntax
| void ApplyImpedancePhi_Hcurl( | int m, int k, int offset, TinyVector phi, TinyVector curl_phi, Vector f_phi) |
This method applies the impedance for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called for the computation of the boundary integral.
where T is the impedance operator, i the row index and j the column index. This method can be overloaded to define your own impedance operator. This method involves only vectorial basis functions (unknown number m is approximated with H(curl) Sobolev space).
Parameters
- m (in)
- unknown number (for rows)
- j (in)
- quadrature point number
- offset (in)
- offset for the unknown m
- phi (in)
- value of basis function (row)
- curl_phi (in)
- curl of basis function (row)
- f_phi (in)
- result vector T(phi, grad_phi)
// for your own impedance operator
class MyOperator : public ImpedanceFunction_Base<Real_wp, Dimension2>
{
void ApplyImpedancePhi_Hcurl(int m, int j, int offset, const TinyVector<Real_wp, 2>& phi,
const TinyVector<Real_wp, 1>& curl_phi, Vector<T>& f_phi)
{
// for a diagonal operator :
Real_wp coef = 4.5; // impedance coefficient
f_phi(offset) = coef*phi(0);
f_phi(offset+1) = coef*phi(1);
}
};
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyImpedanceCurl
Syntax
| void ApplyImpedanceCurl( | int m, int k, int offset, TinyVector phi, TinyVector curl_phi, Vector f_phi) |
This method applies the impedance for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called for the computation of the boundary integral.
where T is the impedance operator, i the row index and j the column index. This method can be overloaded to define your own impedance operator. This method involves only vectorial basis functions (unknown number m is approximated with H(curl) Sobolev space).
Parameters
- m (in)
- unknown number (for rows)
- j (in)
- quadrature point number
- offset (in)
- offset for the unknown m
- phi (in)
- value of basis function (row)
- curl_phi (in)
- curl of basis function (row)
- f_phi (in)
- result vector T(phi, grad_phi)
// for your own impedance operator
class MyOperator : public ImpedanceFunction_Base<Real_wp, Dimension2>
{
void ApplyImpedancePhi_Hcurl(int m, int j, int offset, const TinyVector<Real_wp, 2>& phi,
const TinyVector<Real_wp, 1>& curl_phi, Vector<T>& f_phi)
{
// for a diagonal operator :
f_phi.Zero();
Real_wp coef = 4.5; // impedance coefficient
f_phi(offset) = coef*phi(0);
f_phi(offset+1) = coef*phi(1);
}
void ApplyImpedanceCurl(int m, int j, int offset, const TinyVector<Real_wp, 2>& phi,
const TinyVector<Real_wp, 1>& curl_phi, Vector<T>& f_phi)
{
// if no gradient term, you can fill with zeros
f_phi.Zero();
}
};
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyImpedancePhi_Hdiv
Syntax
| void ApplyImpedancePhi_Hdiv( | int m, int k, int offset, TinyVector phi, TinyVector div_phi, Vector f_phi) |
This method applies the impedance for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called for the computation of the boundary integral.
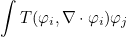
where T is the impedance operator, i the row index and j the column index. This method can be overloaded to define your own impedance operator. This method involves only vectorial basis functions (unknown number m is approximated with H(div) Sobolev space).
Parameters
- m (in)
- unknown number (for rows)
- j (in)
- quadrature point number
- offset (in)
- offset for the unknown m
- phi (in)
- value of basis function (row)
- div_phi (in)
- divergence of basis function (row)
- f_phi (in)
- result vector T(phi, grad_phi)
// for your own impedance operator
class MyOperator : public ImpedanceFunction_Base<Real_wp, Dimension2>
{
void ApplyImpedancePhi_Hdiv(int m, int j, int offset, const TinyVector<Real_wp, 2>& phi,
const TinyVector<Real_wp, 1>& div_phi, Vector<T>& f_phi)
{
// for a diagonal operator :
Real_wp coef = 4.5; // impedance coefficient
f_phi(offset) = coef*phi(0);
f_phi(offset+1) = coef*phi(1);
}
};
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
ApplyImpedanceDiv
Syntax
| void ApplyImpedanceCurl( | int m, int k, int offset, TinyVector phi, TinyVector div_phi, Vector f_phi) |
This method applies the impedance for a given quadrature point. In the method AddMatrixImpedanceBoundary, this method is called for the computation of the boundary integral.
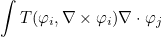
where T is the impedance operator, i the row index and j the column index. This method can be overloaded to define your own impedance operator. This method involves only vectorial basis functions (unknown number m is approximated with H(div) Sobolev space).
Parameters
- m (in)
- unknown number (for rows)
- j (in)
- quadrature point number
- offset (in)
- offset for the unknown m
- phi (in)
- value of basis function (row)
- div_phi (in)
- divergence of basis function (row)
- f_phi (in)
- result vector T(phi, grad_phi)
// for your own impedance operator
class MyOperator : public ImpedanceFunction_Base<Real_wp, Dimension2>
{
void ApplyImpedancePhi_Hdiv(int m, int j, int offset, const TinyVector<Real_wp, 2>& phi,
const TinyVector<Real_wp, 1>& div_phi, Vector<T>& f_phi)
{
// for a diagonal operator :
f_phi.Zero();
Real_wp coef = 4.5; // impedance coefficient
f_phi(offset) = coef*phi(0);
f_phi(offset+1) = coef*phi(1);
}
void ApplyImpedanceDiv(int m, int j, int offset, const TinyVector<Real_wp, 2>& phi,
const TinyVector<Real_wp, 1>& div_phi, Vector<T>& f_phi)
{
// if no gradient term, you can fill with zeros
f_phi.Zero();
}
};
Location :
Harmonic/BoundaryConditionHarmonic.hxx
Harmonic/BoundaryConditionHarmonic.cxx
Constructor for TransparencySolver
Syntax
| TransparencySolver( | EllipticProblem& var, All_LinearSolver& solver) |
The constructor takes the considered problem to solve as argument. If you do not have an EllipticProblem instance, but rather a VarProblem_Base instance (if you are writing in a generic function), you can call GetNewTransparentSolver that will construct an object TransparencySolver and return a pointer of type TransparencySolver_Base.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b (with only first-order ABC)
VectComplex_wp x = b; solver->ComputeSolution(x);
// then you construct your transparent solver
TransparencySolver<HelmholtzEquation<Dimension2> > solver_transp(var, *solver);
ReadInputFile("test.ini", solver_transp);
// and you can iterate on the solution to obtain the exact solution
if (solver_transp.UseTransparentCondition())
{
solver_transp.Init();
VectComplex_wp source_rhs(x);
solver_transp.Solve(x, source_rhs);
}
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
UseTransparentCondition
Syntax
| bool UseTransparentCondition() const |
This method returns true if a transparent condition has been set.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b (with only first-order ABC)
VectComplex_wp x = b; solver->ComputeSolution(x);
// then you construct your transparent solver
TransparencySolver<HelmholtzEquation<Dimension2> > solver_transp(var, *solver);
ReadInputFile("test.ini", solver_transp);
// and you can iterate on the solution to obtain the exact solution
if (solver_transp.UseTransparentCondition())
{
solver_transp.Init();
VectComplex_wp source_rhs(x);
solver_transp.Solve(x, source_rhs);
}
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
Solve
Syntax
| void Solve(Vector& x_sol, Vector& b_src) const |
This method fills the vector x_sol to contain the solution with a transparent condition. The input vector b_src contains the solution with a first-order absorbing boundary condition.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b (with only first-order ABC)
VectComplex_wp x = b; solver->ComputeSolution(x);
// then you construct your transparent solver
TransparencySolver<HelmholtzEquation<Dimension2> > solver_transp(var, *solver);
ReadInputFile("test.ini", solver_transp);
// and you can iterate on the solution to obtain the exact solution
if (solver_transp.UseTransparentCondition())
{
solver_transp.Init();
VectComplex_wp source_rhs(x);
solver_transp.Solve(x, source_rhs);
}
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
Init
Syntax
| void Init() |
This method initializes the computation of the transparent condition. It will compute quadrature points and weights for the two surfaces (absorbing surface and intermediary surface).
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b (with only first-order ABC)
VectComplex_wp x = b; solver->ComputeSolution(x);
// then you construct your transparent solver
TransparencySolver<HelmholtzEquation<Dimension2> > solver_transp(var, *solver);
ReadInputFile("test.ini", solver_transp);
// and you can iterate on the solution to obtain the exact solution
if (solver_transp.UseTransparentCondition())
{
solver_transp.Init();
VectComplex_wp source_rhs(x);
solver_transp.Solve(x, source_rhs);
}
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeSolution
Syntax
| void ComputeSolution(Vector& rhs, Vector& sol) |
This method computes the solution of the sparse finite element matrix As sol = rhs.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// then you construct your transparent solver
TransparencySolver<HelmholtzEquation<Dimension2> > solver_transp(var, *solver);
ReadInputFile("test.ini", solver_transp);
// we solve the linear system A_s x = b (with only first-order ABC)
VectComplex_wp x = b; solver_transp.ComputeSolution(b, x);
// and you can iterate on the solution to obtain the exact solution
if (solver_transp.UseTransparentCondition())
{
solver_transp.Init();
VectComplex_wp source_rhs(x);
solver_transp.Solve(x, source_rhs);
}
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeGreenKernel
Syntax
| void ComputeGreenKernel(const R3& x, const R3& y, const Real_wpp& k, Complex_wp& phi, R3_Complex_wp& grad_phi, Matrix3_3sym_Complex_wp& hessian_phi) |
| void ComputeGreenKernel(const R3& x, const R3& y, const Real_wpp& k, Complex_wp& phi, R3_Complex_wp& grad_phi) |
This static method computes the Green kernel (for wave equation), its gradient (with respect to y) and hessian matrix. You can also compute only the kernel and its gradient. This Green's kernel is equal to
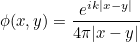
Parameters
- x (in)
- point
- y (in)
- point
- k (in)
- wave number
- phi (out)
- Green's kernel phi(x, y)
- grad_phi (out)
- gradient of Green's kernel
- hessian_phi (out, optional)
- hessian of Green's kernel
int main()
{
// you choose two points
R3 x(0.1, 0.5, 0.3), y(0.2, 2.0, 0.8);
// a wave number
Real_wp k = 0.3;
// Green's kernel and gradient for these values
Complex_wp phi;
R3_Complex_wp grad_phi; Matrix3_3sym_Complex_wp hessian_phi;
TransparencySolver_Base::ComputeGreenKernel(x, y, k, phi, grad_phi, hessian_phi);
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeSurfaceGammaAndAbsorbing
Syntax
| void ComputeSurfaceGammaAndAbsorbing(int ref_abc, int ref_gamma, IVect& offset_abc_proc) |
This internal method computes the quadrature points for the intermediary surface (denoted Gamma) and for the absorbing surface (denoted sigma). ref_abc is the boundary condition associated with the absorbing surface (usually equal to BoundaryConditionEnum::LINE_ABSORBING. ref_gamma is the body number for the intermediary surface (all references such that the body number is equal to ref_gamma will belong to this intermediary surface). The output argument offset_abc_proc stores the offsets for quadrature points of the absorbing surface. On regular use, this methods does not need to be called, since the method Init will call it automatically.
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeRightHandSide
Syntax
| void ComputeRightHandSide(const VectComplex_wp& x_sol, VectComplex_wp& g_source) |
This internal method computes the matrix-vector product g_source = Ad x_sol where Ad is introduced in the section devoted to transparent conditions. On regular use, this method does not need to be called, since the method Solve will call it automatically.
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeIntegralRepresentation
Syntax
| void ComputeIntegralRepresentation( | const VectComplex_wp& trace_En, const VectComplex_wp& trace_Hn, const MeshInterpolation& mesh_gamma, |
| const R_N& x, const R_N& n, TinyVector& En, TinyVector& Hn) |
This method computes the value of E x n and H x n on a given point from values on the quadrature points of the intermediary surface Gamma (by using an integral representation). On regular use, this method does not need to be called, since the method Solve will call it automatically. This method is virtual such that it is overloaded for each equation where it is implemented.
Parameters
- trace_En (in)
- values of E x n on quadrature points of Gamma
- trace_Hn (in)
- values of H x n on quadrature points of Gamma
- mesh_gamma (in)
- surface mesh Gamma
- x (in)
- point where E x n will be evaluated
- n (in)
- outgoing normale associated with the point x
- En (out)
- evaluation of E x n at x (with the given normale)
- Hn (out)
- evaluation of H x n at x (with the given normale)
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeAndStoreEnPot
Syntax
| void ComputeAndStoreEnPot(const VectComplex_wp& trace_En, const VectComplex_wp& trace_Hn, const R_N& x, const R_N& n, Vector& En, Vector& Hn, int k) |
This method computes the value of E x n and H x n on a given point from values on the quadrature points of the intermediary surface Gamma (by using an integral representation). On regular use, this method does not need to be called, since the method Solve will call it automatically. This method is virtual such that it is overloaded for each equation where it is implemented. This method actually calls ComputeIntegralRepresentation and inserts the results on the global vectors En and Hn .
Parameters
- trace_En (in)
- values of E x n on quadrature points of Gamma
- trace_Hn (in)
- values of H x n on quadrature points of Gamma
- x (in)
- point where E x n will be evaluated
- n (in)
- outgoing normale associated with the point x
- EnStore (inout)
- evaluation of E x n for all points of Sigma
- HnStore (out)
- evaluation of H x n for all points of Sigma
- k (out)
- number of the point x (it corresponds to the position where E x n and H x n will be inserted in EnStore and HnStore)
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
GetSource
Syntax
| void GetSource( | const VectComplex_wp& trace_En, const VectComplex_wp& trace_Hn, int n, Real_wp k, |
| const R_N& ptX, const R_N& normaleX, Vector& g_source, int k_loc) |
This method computes the source term g, that appears in the matrix Ad. This matrix will be equal to
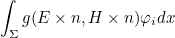
On regular use, this method does not need to be called, since the method Solve will call it automatically. This method is virtual such that it is overloaded for each equation where it is implemented.
Parameters
- trace_En (in)
- values of E x n on quadrature points of Sigma
- trace_Hn (in)
- values of H x n on quadrature points of Sigma
- n (in)
- global point number where g needs to be evaluated
- k (in)
- wave number at infinity
- ptX (in)
- point where g needs to be evaluated
- normaleX (out)
- outgoing normale associated with ptX
- g_source (inout)
- source term that will be modified for the considered quadrature point
- j (in)
- local quadrature point
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
RcsToBeComputed
Syntax
| bool RcsToBeComputed() |
This method will return true if the computation of a radar cross section is asked by the user.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
if (var_rcs.RcsToBeComputed())
cout << "RCS has to be computed" << endl;
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
GetNbAngles
Syntax
| int GetNbAngles() |
This method returns the number of angles required for the radar cross section. This number is usually set by inserting a line AngleRCS = 0.0 180.0 181 in the data file.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
if (var_rcs.RcsToBeComputed())
cout << "Number of angles for the RCS = " << var_rcs.GetNbAngles() << endl;
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
GetNbPointsOutside
Syntax
| int GetNbPointsOutside() |
This method returns the number of points outside the computational domain for which the user wants to evaluate the solution. For these points, the field will be computed with an integral representation. This number is usually set by inserting a line SismoOutsidePoints = pts.txt diffrac.dat total.dat 0.1 in the data file.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
if (var_rcs.RcsToBeComputed())
cout << "Number of points outside = " << var_rcs.GetNbPointsOutside() << endl;
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
GetRcsType
Syntax
| int GetRcsType() |
This method returns the type of radar cross section to be computed. This type is usually set by inserting a line ParametersRCS = YES 1 AUTO BISTATIC in the data file. The integer can be equal to VarComputationRCS_Base<Dimension>::MONOSTATIC_RCS or VarComputationRCS_Base<Dimension>::BISTATIC_RCS.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
if (var_rcs.RcsToBeComputed())
if (var_rcs.GetRcsType() == var_rcs.MONOSTATIC_RCS)
cout << "computation of a monostatic radar cross section" << endl;
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
GetOutsidePoint
Syntax
| const VectR_N& GetOutsidePoint() |
| const R_N& GetOutsidePoint(int i) |
This method returns the points outside the computational domain for which the user wants to evaluate the solution. For these points, the field will be computed with an integral representation. These points are usually set by inserting a line SismoOutsidePoints = pts.txt diffrac.dat total.dat 0.1 in the data file.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
// to retrieve all the points outside the computational domain
const VectR2& pts_outside = var_rcs.GetOutsidePoint();
// to retrieve a single point
int num_pt = 2;
const R2& pt = var_rcs.GetOutsidePoint(num_pt);
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
SetOutsidePoints
Syntax
| void SetOutsidePoints(const VectR_N& pts) |
This method sets the points outside the computational domain for which the user wants to evaluate the solution. For these points, the field will be computed with an integral representation. These points are usually set by inserting a line SismoOutsidePoints = pts.txt diffrac.dat total.dat 0.1 in the data file.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
// if you want to change the list of outside points
VectR2 pts(2);
pts(0).Init(5.0, 2.0);
pts(1).Init(8.0, 1.0);
var_rcs.SetOutsidePoints(pts);
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
GetInterpolationMesh
Syntax
| MeshInterpolationFEM& GetInterpolationMesh() |
This method returns the mesh of the surface used to compute the radar cross section. This mesh contains quadrature points and normales.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
var_rcs.InitComputationRCS(); // actually useless, since already called above in ConstructAll
const MeshInterpolationFEM<Dimension2>& surf_mesh = var_rcs.GetInterpolationMesh();
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
SetTimeStep
Syntax
| void SetTimeStep(Real_wp dt) |
This method sets the time step used for unsteady simulations.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
var_rcs.SetTimeStep(0.1);
var_rcs.InitComputationRCS();
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
InitComputationRCS
Syntax
| void InitComputationRCS(bool assemble = false) |
This method initializes the computation of the radar cross section. It mainly computes the quadrature points and normales for the surface used to compute the integrals.
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
var_rcs.InitComputationRCS(); // actually useless, since already called above in ConstructAll
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeRCS
Syntax
| void ComputeRCS(VectComplex_wp x_sol) |
This method computes the radar cross section for the solution given as argument. The results are written in the file given in the datafile (FileRCS = Rcs.dat).
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
var_rcs.InitComputationRCS(); // actually useless, since already called above in ConstructAll
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b (with only first-order ABC)
VectComplex_wp x = b; solver->ComputeSolution(x);
// computation of the radar cross section for this solution
var_rcs.ComputeRCS(x);
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx
ComputeIntegralRepresentation
Syntax
| void ComputeIntegralRepresentation( | const VectComplex_wp& trace_En, const VectComplex_wp& trace_Hn, |
| const MeshInterpolationFEM& mesh, R_N ptX, VectComplex_wp& u) |
This method computes the solution on a point outside the computational domain with an integral representation.
Parameters
- trace_En (in)
- values of E x n on quadrature points on the surface of integration
- trace_Hn (in)
- values of H x n on quadrature points on the surface of integration
- mesh (in)
- mesh of the surface
- ptX (in)
- point where the solution needs to be evaluated
- u (out)
- result
int main()
{
EllipticProblem<HelmholtzEquation<Dimension2> > var;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "HELMHOLTZ", solver);
// an object VarComputationRCS is contained in var :
VarComputationRCS<HelmholtzEquation<Dimension2> >& var_rcs = var.output_rcs_param;
var_rcs.InitComputationRCS(); // actually useless, since already called above in ConstructAll
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b (with only first-order ABC)
VectComplex_wp x = b; solver->ComputeSolution(x);
// computation of E x n and H x n on the surface of integration
VectComplex_wp traceEn, traceHn;
var.ComputeEnHnOnBoundary(var_rcs.GetInterpolationMesh(), x, traceEn, traceHn, false);
// if you want to know the solution on a point outside the computational domain
R2 ptX(3.0, 0.8); VectComplex_wp u(1);
var_rcs.ComputeIntegralRepresentation(traceEn, traceHn, var_rcs.GetInterpolationMesh(), ptX, u);
}
Location :
Harmonic/TransparencyCondition.hxx
Harmonic/TransparencyCondition.cxx