Finite element classes
In order to use finite element classes, you can include MontjoieFiniteElement.hxx or Montjoie.hxx. In Montjoie, there are three families of finite elements implemented :
- scalar finite elements : they can be used to approximate H1 space. The basis functions are scalar. This is the most common type of finite elements in the literature. For triangles/tetrahedra, it corresponds to the
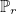 polynomial space, whereas for quadrangles/hexahedra, it corresponds to the
polynomial space, whereas for quadrangles/hexahedra, it corresponds to the
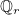 polynomial space.
polynomial space.
- edge elements : they can be used to approximate H(curl) space. The basis functions are vectorial (with three components in 3-D). These elements are also known as Nédélec's elements in the literature.
- facet elements : they can be used to approximate H(div) space. The basis functions are vectorial (with three components in 3-D). These elements are also known as Raviart-Thomas elements in the literature.
In Montjoie, we can use a discontinuous formulation in conjunction with a finite element class. The discontinuity is ensured when the mesh is numbered (see class MeshNumbering, and function SetFormulationDG).
General structure
Finite elements in Montjoie are based on a reference element (usually denoted
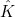 ). This reference element is for example the unit square [0, 1]2 for quadrilaterals. The transformation Fi transforms the reference element
). This reference element is for example the unit square [0, 1]2 for quadrilaterals. The transformation Fi transforms the reference element
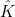 to the real element Ki where i is the element number. The basis functions in the real element
to the real element Ki where i is the element number. The basis functions in the real element
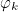 are constructed from basis functions
are constructed from basis functions
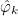 on the reference element with the relation (for scalar finite elements)
on the reference element with the relation (for scalar finite elements)
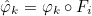
In the page devoted to the transformation Fi, reference elements and transformations Fi are detailed.
A finite element object consists of :
- Geometrical shape functions, which are used for transformation Fi
(especially when the element is curved) :
where Ai are nodal points of the element
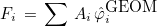
- Quadrature formulas (points and weights of integration) for volume and boundary integrals.
- Basis functions and their derivatives (gradient or curl). The
approximate solution is then searched as :
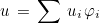
You can associate a different order for each of this feature, i.e. an order for approximation of the geometry, an order for integration, and an order of approximation. Usually, all these orders are equal but it may be interesting to specify different orders.
For finite element classes, we define the following operators
- Operator Ch stores the values of basis functions on quadrature points :
where
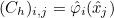
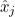 are quadrature points on the reference element
are quadrature points on the reference element
- Operator Rh stores the gradient of basis functions on quadrature points :
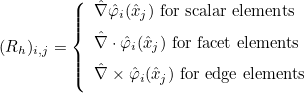
- Operator Sh stores the values of basis functions on quadrature points of a face :
where
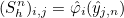
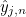 are quadrature points on the face n (edge in 2-D) of the reference element
are quadrature points on the face n (edge in 2-D) of the reference element
We also define the mass matrix as the following matrix
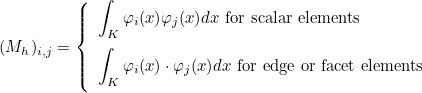
Basic Use
#include "FiniteElement/MontjoieFiniteElement.hxx"
int main(int argc, char** argv)
{
InitMontjoie(argc, argv);
// declaration of a nodal tetrahedron
TetrahedronClassical Fb;
// you construct the finite element
int r = 4;
Fb.ConstructFiniteElement(r);
// then you can use any method of this finite element
int nb_pts_quad = Fb.GetNbPointsQuadratureInside();
int nb_dof = Fb.GetNbDof();
Vector<double> feval(nb_pts_quad);
// integration against basis functions
// contrib_i = \int exp(-r^2)* varphi_i
for (int i = 0; i < nb_pts_quad; i++)
feval(i) = Fb.WeightsND(i)*exp(-DotProd(Fb.PointsND(i), Fb.PointsND(i)));
Vector<double> contrib(nb_dof);
Fb.ComputeIntegralRef(feval, contrib);
// computation of \hat{\varphi}_i(x) for all i :
Vector<double> phi;
R3 x(0.4, 0.5, 0.01);
Fb.ComputeValuesPhiRef(x, phi);
// and gradient
VectR3 grad_phi;
Fb.ComputeGradientPhiRef(x, grad_phi);
return FinalizeMontjoie();
}
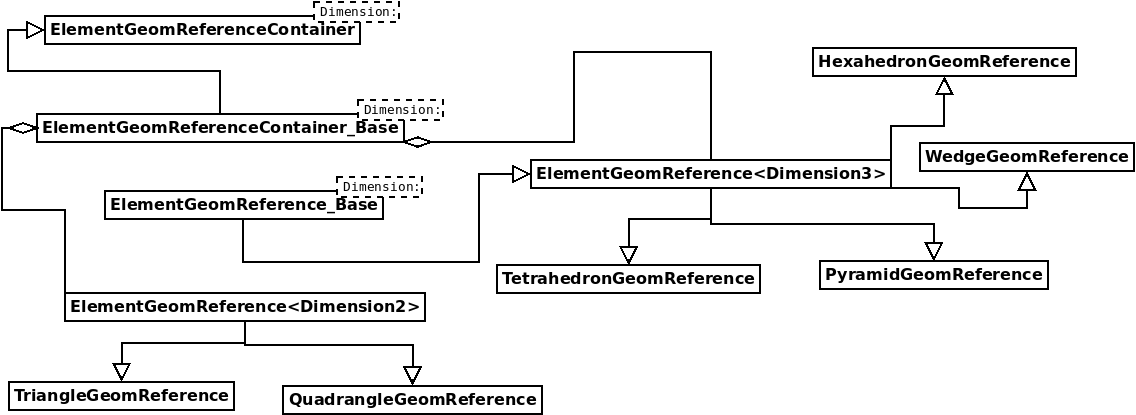
Geometric finite elements
For the definition of shape functions, the classes TriangleGeomReference, QuadrangleGeomReference (in 2-D), TetrahedronReference, PyramidGeomReference, WedgeGeomReference, HexahedronGeomReference have been written. They are used in the Mesh class in order to handle curved elements. Below, we represent the inheritance diagram of these classes:
These classes can be used by including only MontjoieMesh.hxx. We show an example of use of these classes below :
TriangleGeomReference tri;
// constructing the shape functions at a given order
int order = 4;
tri.ConstructFiniteElement(order);
// then you can evalue shape functions on a point
R2 point(0.2, 0.3); VectReal_wp phi;
tri.ComputeValuesPhiNodalRef(point, phi);
// and gradients :
VectR2 grad_phi;
tri.ComputeGradientPhiNodalRef(point, phi);
// you can also compute Fi for all the nodal points
Mesh<Dimension2> mesh;
mesh.SetGeometryOrder(order); mesh.Read("test.msh");
int num_elem = 13; VectR2 s;
mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension2> PointsElem;
tri.FjElemNodal(s, PointsElem, mesh, num_elem);
Intermediary classes such as ElementGeomReference or ElementGeomReference_Base are abstract classes and should not be instantiated. The class ElementGeomReferenceContainer is an interface class to call methods of the leaf class (e.g. TriangleGeomReference, QuadrangleGeomReference) and is used by finite element classes.
Finite element classes
The main classes to consider are TriangleReference, QuadrangleReference (in 2-D) and TetrahedronReference, PyramidReference, WedgeReference and HexahedronReference (in 3-D). These template classes are depending on an integer (named type). If type is equal to 1, we consider that the leaf class will be a scalar finite element (to approximate H1 space), whereas if it is equal to 2, the leaf class will implement an edge element (to approximate H(curl) space). If the type is equal to 3, the leaf class will implement a facet element (to approximate H(div) space). Leaf classes (such as TriangleClassical, QuadrangleLobatto, TetrahedronClassical, etc) that are used in practice will derive from those classes (i.e. TriangleReference, QuadrangleReference, etc). In the diagrams below, we show the hierarchy of classe in 2-D :
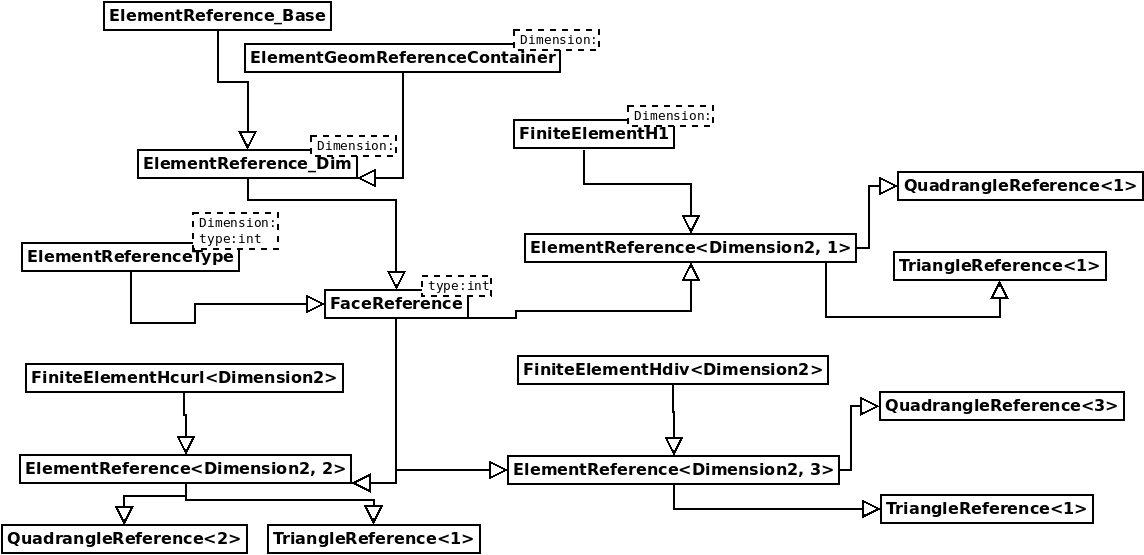
and similarly in 3-D :
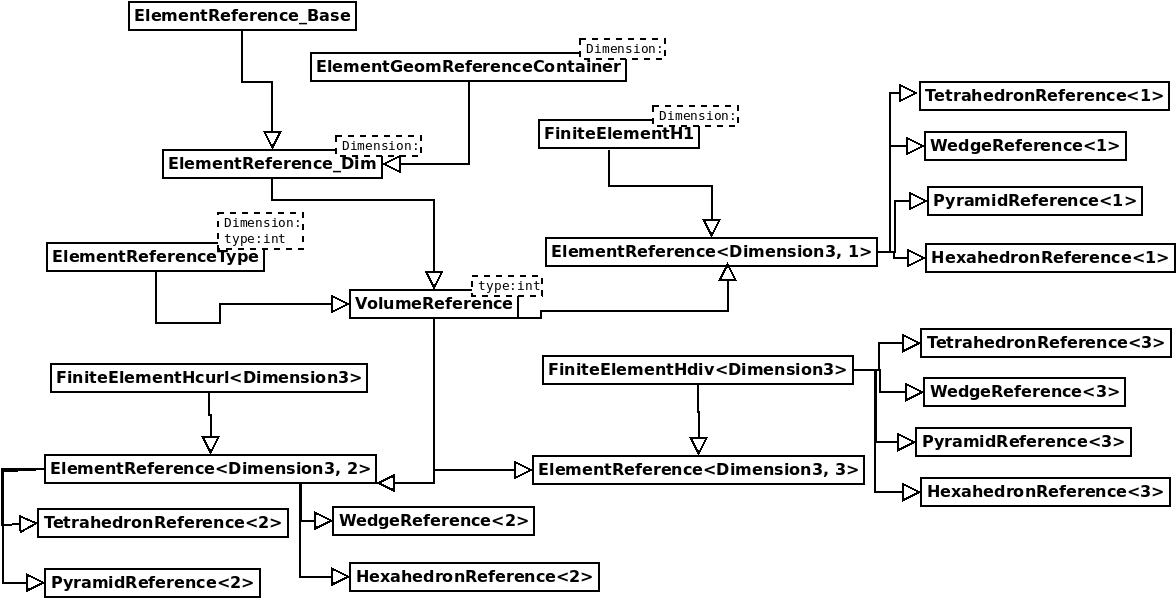
Intermediary classes such as ElementReference_Base, ElementReference, FaceReference, VolumeReference or FiniteElementH1 are abstract classes and should not be instantiated.
How to create a new finite element
Scalar finite elements
For the definition of a new finite element, you have to derive the class TriangleReference<1> (if your finite element is adapted to triangular elements) or QuadrangleReference<1> (for quadrilaterals) or TetrahedronReference<1> (for tetrahedra) or PyramidReference<1> (for pyramids) or WedgeReference<1> (for triangular prisms) or HexahedronReference<1> (for hexahedra). For example if you want to write a new tetrahedral finite element, you can write :
// replace TetrahedronReference by PyramidReference, WedgeReference or HexahedronReference
// for a pyramidal, prismatic or hexahedral element
class MyFiniteElement : public TetrahedronReference<1>
{
public :
// number of dofs on each edge, triangle, tetrahedron, etc ?
void ConstructNumberMap(NumberMap& map, int dg) const;
// main method used to construct the finite element object
// r : order of approximation for basis functions
// rgeom : order of approximation for geometry (shape functions)
// rquad : order of quadrature
// if rgeom is equal to 0 (and similarly rquad equal to 0)
// we are considering that rgeom = r, and rquad = r
// if type_quad is equal to -1, we use the default quadrature
// formulas (probably Gauss formulas)
// rsurf_tri, rsurf_quad : orders for boundary integrals
// type_surf_tri, type_surf_quad : type of integration for triangles and quadrangles
void ConstructFiniteElement(int r, int rgeom = 0, int rquad = 0, int type_quad = -1,
int rsurf_tri = 0, int rsurf_quad = 0, int type_surf_tri = -1,
int type_surf_quad = -1, int gauss_z = -1);
// computation of phi_i(x) for a given point x
// the values phi_i(x) have to be placed in the array phi
void ComputeValuesPhiRef(const R3& x, VectReal_wp& phi) const;
// computation of \nabla phi_i(x) for a given point x
void ComputeGradientPhiRef(const R3& x, VectR3& grad_phi) const;
};
// for 2-D finite elements : TriangleReference or QuadrangleReference
class MyFiniteElement2D : public TriangleReference<1>
{
public :
void ConstructFiniteElement(int r, int rgeom = 0, int rquad = 0, int type_quad = -1,
int rsurf = 0, int type_surf = -1);
void ComputeValuesPhiRef(const R2& x, VectReal_wp& phi) const;
void ComputeGradientPhiRef(const R2& x, VectR2& grad_phi) const;
};
Once you defined your finite element, you may want to link it with the class EllipticProblem in order to use your new finite element to solve a standard equation (such as Helmholtz equation). This procedure is detailed in the page describing the class VarFiniteElement.
Edge finite elements
For the definition of a new edge finite element, the minimal class to write is close to the scalar case :
// replace TetrahedronReference by PyramidReference, WedgeReference or HexahedronReference
// for a pyramidal, prismatic or hexahedral element
class MyFiniteElement : public TetrahedronReference<2>
{
public :
// main method used to construct the finite element object
// r : order of approximation for basis functions
// rgeom : order of approximation for geometry (shape functions)
// rquad : order of quadrature
// if rgeom is equal to 0 (and similarly rquad equal to 0)
// we are considering that rgeom = r, and rquad = r
// if type_quad is equal to -1, we use the default quadrature
// formulas (probably Gauss formulas)
void ConstructFiniteElement(int r, int rgeom = 0, int rquad = 0, int type_quad = -1,
int rsurf_tri = 0, int rsurf_quad = 0, int type_surf_tri = -1,
int type_surf_quad = -1, int gauss_z = -1);
// computation of phi_i(x) for a given point x
// the values phi_i(x) have to be placed in the array phi
void ComputeValuesPhiRef(const R3& x, VectR3& phi) const;
// computation of curl phi_i(x) for a given point x
void ComputeCurlPhiRef(const R3& x, VectR3& curl_phi) const;
};
// for 2-D finite elements : TriangleReference or QuadrangleReference
class MyFiniteElement2D : public TriangleReference<2>
{
public :
void ConstructFiniteElement(int r, int rgeom = 0, int rquad = 0, int type_quad = -1,
int rsurf = 0, int type_surf = -1);
void ComputeValuesPhiRef(const R2& x, VectR2& phi) const;
void ComputeGradientPhiRef(const R2& x, VectReal_wp& curl_phi) const;
};
If you want to link your new class with the class EllipticProblem in order to use your new finite element to solve a standard equation (such as Maxwell's equation), take a look at the class VarFiniteElement.
Facet finite elements
For the definition of a new facet finite element, the minimal class to write is close to the scalar case :
// replace TetrahedronReference by PyramidReference, WedgeReference or HexahedronReference
// for a pyramidal, prismatic or hexahedral element
class MyFiniteElement : public TetrahedronReference<3>
{
public :
// main method used to construct the finite element object
// r : order of approximation for basis functions
// rgeom : order of approximation for geometry (shape functions)
// rquad : order of quadrature
// if rgeom is equal to 0 (and similarly rquad equal to 0)
// we are considering that rgeom = r, and rquad = r
// if type_quad is equal to -1, we use the default quadrature
// formulas (probably Gauss formulas)
void ConstructFiniteElement(int r, int rgeom = 0, int rquad = 0, int type_quad = -1,
int rsurf_tri = 0, int rsurf_quad = 0, int type_surf_tri = -1,
int type_surf_quad = -1, int gauss_z = -1);
// computation of phi_i(x) for a given point x
// the values phi_i(x) have to be placed in the array phi
void ComputeValuesPhiRef(const R3& x, VectR3& phi) const;
// computation of div phi_i(x) for a given point x
void ComputeCurlPhiRef(const R3& x, VectReal_wp& div_phi) const;
};
// for 2-D finite elements : TriangleReference or QuadrangleReference
class MyFiniteElement2D : public TriangleReference<3>
{
public :
void ConstructFiniteElement(int r, int rgeom = 0, int rquad = 0, int type_quad = -1,
int rsurf = 0, int type_surf = -1);
void ComputeValuesPhiRef(const R2& x, VectR2& phi) const;
void ComputeGradientPhiRef(const R2& x, VectReal_wp& curl_phi) const;
};
If you want to link your new class with the class EllipticProblem in order to use your new finite element to solve a standard equation (such as Helmholtz equation), take a look at the class VarFiniteElement.
Methods of ElementGeomReference_Base
The class ElementGeomReference_Base is the base class for geometric finite elements (that define shape functions used for curved elements).
| GetGeometryOrder | returns the order of shape functions |
| NormaleLoc | returns the outward normale to a face of the reference element |
| PointsNodal1D | returns nodal points on the unit interval |
| PointsNodalND | returns coordinates of a nodal point |
| WeightsNodalND | returns weight of a nodal point |
| PointsDof1D | returns dof points on the unit interval |
| Points1D | returns quadrature points on the unit interval |
| Weights1D | returns quadrature weights on the unit interval |
| GetHybridType | returns the hybrid type of the element |
| GetNbVertices | returns the number of vertices of the element |
| GetNbEdges | returns the number of edges of the element |
| GetNbBoundaries | returns the number of faces of the element |
| SetAxisymmetricGeometry | informs that the geometry is the section of an axisymmetric domain |
| GetSurfaceFiniteElement | returns the finite element for a face of the element |
| SetMesh | initialization of the finite element with a mesh |
| GetNormale | returns the outward normale on the real element from the inverse of the jacobian matrix |
| FjCurvePhi | computes Fi(x) and fills shape functions |
| DFjCurvePhi | computes DFi(x) and fills shape functions |
| GetMemorySize | returns the size used by the object in bytes |
| GetCenterReferenceElement | returns the center of the reference element |
| ConstructFiniteElement | constructs the finite element at a given order |
| GetNewNodalInterpolation | returns a new projector class |
| Fj | computes the image of a given point by the transformation Fi |
| FjLinear | computes the image of a given point by the transformation Fi for straight elements |
| DFj | computes the jacobian matrix DFi for a given point |
| DFjLinear | computes the jacobian matrix DFi for a given point for straight elements |
| GetMinimalSize | returns the minimal length of edges of the element |
| OutsideReferenceElement | returns true if the given point is outside the reference element |
| GetDistanceToBoundary | returns the distance of a given point to the boundary of the reference element (negative if the point is outside) |
| ProjectPointOnBoundary | projects points on the boundary of the reference element |
| ComputeCoefJacobian | computes coefficients appearing in the expression of the jacobian |
| FjElem | Computes images of dof, nodal and quadrature points by the transformation Fi |
| FjElemNodal | Computes images of nodal points by the transformation Fi |
| FjElemQuadrature | Computes images of quadrature points by the transformation Fi |
| FjElemDof | Computes images of dof points by the transformation Fi |
| DFjElem | Computes jacobian matrices DFi for dof, nodal and quadrature points |
| DFjElemNodal | Computes jacobian matrices DFi for nodal points |
| DFjElemQuadrature | Computes jacobian matrices DFi for quadrature points |
| DFjElemDof | Computes jacobian matrices DFi for dof points |
| ComputeValuesNodalPhi1D | computes values of 1-D shape functions on a given point |
| ComputeValuesPhiNodalRef | computes nodal shape functions on the reference element for a given point |
| ComputeGradientPhiNodalRef | computes gradient of nodal shape functions on the reference element for a given point |
| ComputeCoefficientTransformation | computes coefficients needed to evaluate transformation Fi quickly |
| ComputeNodalGradientRef | computes gradient on nodal points of a function from its values on nodal points |
| ComputeNodalGradient | computes gradient on nodal points of a function from its values on nodal points |
Methods of ElementGeomReferenceContainer_Base
The class ElementGeomReferenceContainer_Base is an interface class to call methods of the geometric finite element directly from any finite element class. The methods below can be called by any finite element class (type derived from ElementReference).
| QuadratureEqualNodal | returns true if quadrature points coincide with nodal points |
| DofEqualNodal | returns true if dof points coincide with nodal points |
| DofEqualQuadrature | returns true if dof points coincide with quadrature points |
| GetGeometryOrder | returns the order of shape functions |
| SetGeometryOrder | sets the order of shape functions |
| GetGeometricElement | gives access to the geometric element |
| NormaleLoc | returns the outward normale to a face of the reference element |
| PointsNodal1D | returns nodal points on the unit interval |
| PointsDof1D | returns dof points on the unit interval |
| Points1D | returns quadrature points on the unit interval |
| Weights1D | returns quadrature weights on the unit interval |
| GetHybridType | returns the hybrid type of the element |
| GetNbVertices | returns the number of vertices of the element |
| GetNbEdges | returns the number of edges of the element |
| GetNbBoundaries | returns the number of faces of the element |
| GetNewNodalInterpolation | returns a new projector class |
| SetMesh | initialization of the finite element with a mesh |
| Fj | computes the image of a given point by the transformation Fi |
| FjLinear | computes the image of a given point by the transformation Fi for straight elements |
| DFj | computes the jacobian matrix DFi for a given point |
| DFjLinear | computes the jacobian matrix DFi for a given point for straight elements |
| GetMinimalSize | returns the minimal length of edges of the element |
| OutsideReferenceElement | returns true if the given point is outside the reference element |
| GetDistanceToBoundary | returns the distance of a given point to the boundary of the reference element (negative if the point is outside) |
| ProjectPointOnBoundary | projects points on the boundary of the reference element |
| ComputeCoefJacobian | computes coefficients appearing in the expression of the jacobian |
| FjElem | Computes images of dof, nodal and quadrature points by the transformation Fi |
| FjElemNodal | Computes images of nodal points by the transformation Fi |
| FjElemQuadrature | Computes images of quadrature points by the transformation Fi |
| FjElemDof | Computes images of dof points by the transformation Fi |
| DFjElem | Computes jacobian matrices DFi for dof, nodal and quadrature points |
| DFjElemNodal | Computes jacobian matrices DFi for nodal points |
| DFjElemQuadrature | Computes jacobian matrices DFi for quadrature points |
| DFjElemDof | Computes jacobian matrices DFi for dof points |
| ComputeValuesNodalPhi1D | computes values of 1-D shape functions on a given point |
| ComputeValuesPhiNodalRef | computes nodal shape functions on the reference element for a given point |
| ComputeGradientPhiNodalRef | computes gradient of nodal shape functions on the reference element for a given point |
| ComputeNodalGradientRef | computes gradient on nodal points of a function from its values on nodal points |
| ComputeNodalGradient | computes gradient on nodal points of a function from its values on nodal points |
Methods of ElementGeomReferenceContainer (inherited from ElementGeomReferenceContainer_Base)
The class ElementGeomReferenceContainer is an interface class to call methods of the geometric finite element directly from any finite element class. The methods below can be called by any finite element class (type derived from ElementReference).
| PointsQuadInsideND | returns the quadrature points associated with volume integrals |
| GetNbPointsNodalElt | returns the number of nodal points in the element |
| GetNbNodalBoundary | returns the number of nodal points on a face of the element |
| GetNumNodes2D/GetNumNodes3D | returns the number of a node from its position (i, j, k) on the reference element |
| GetCoordinateNodes2D/GetCoordinateNodes3D | returns the position (i, j, k) of a node on the reference element |
| PointsNodalBoundary | returns coordinates of a nodal point of a face |
| PointsNodalND | returns coordinates of a nodal point |
| GetNodalNumber | returns the number of a node from its local number on a face of the reference element |
| GetNodalShapeFunctions1D | returns the object Globatto defining the shape functions for the unit interval |
| PointsND | returns coordinates of a quadrature point |
| WeightsND | returns the weight associated with a quadrature point |
| PointsQuadND | returns inside quadrature points + boundary quadrature points |
| PointsDofBoundary | returns dof points of a face |
| PointsQuadratureBoundary | returns a quadrature point of a face |
| WeightsQuadratureBoundary | returns a quadrature weight of a face |
| GetNbPointsDof | returns the number of dof points on the element |
| PointsDofND | returns coordinates of a dof point |
| GetNbPointsQuadrature | returns the number of quadrature points in the element |
| GetNbQuadBoundary | returns the number of quadrature points on a face of the element |
| GetLocalCoordOnBoundary | returns coordinates of a point on the reference element from its local coordinates on the face |
Methods of ElementReference_Base
The class ElementReference_Base is the base class for finite element classes. This class regroups methods that does not depend on the dimension. The methods below can be called by any finite element class (type derived from ElementReference).
| LumpedMassMatrix | returns true if the mass matrix is lumped |
| MassLumpingOrthogonalElement | returns true if the mass matrix is lumped for an orthogonal element (e.g. parallelepiped) |
| DiagonalMassMatrix | returns true if the mass matrix is diagonal |
| DiscontinuousElement | returns true if the finite element can be used only with a discontinuous Galerkin formulation |
| UsePiolaTransform | returns true if the Piola transform is used (for vectorial elements) |
| SetPiolaTransform | enables/disables the use of Piola transform |
| OptimizedComputationMassMatrix | returns true if there is a method implementing an optimized computation of the mass matrix |
| OptimizedComputationElementaryMatrix | returns true if there is a method implementing an optimized computation of the elementary matrix |
| SparseMassMatrix | returns true if the mass matrix is sparse |
| LinearSparseMassMatrix | returns true if the mass matrix for straight elements is sparse |
| UseQuadraturePointsForSh | returns true if the product with matrix Sh is using the value of u on quadrature points |
| UseQuadraturePointsForRh | returns true if the product with matrix Rh is using the value of u on quadrature points |
| UseQuadratureFreeSh | returns true if matrix Sh is evaluated without quadrature |
| GetMaximalOrderRestriction | returns the maximal order used to store the restricttion matrix |
| GetOrder | returns the order of basis functions |
| GetQuadratureOrder | returns the order of quadrature formulas |
| GetNbDof | returns the number of degrees of freedom |
| GetNbPointsQuadratureInside | returns the number of quadrature points used for volume integrals |
| GetNbPointsQuadBoundaries | returns the number of quadrature points used for surface integrals |
| GetNbPointsUsedForSh | returns the number of points used for evaluation of Sh |
| GetNbDofBoundaries | returns the number of dofs not associated with the interior |
| GetNbPointsDofInside | returns the number of dof points inside the element |
| GetNbPointsDofSurface | returns the number of dof points on a boundary of the element |
| GetPointDofNumber | returns the number of a dof point on a boundary of the element |
| GetQuadNumber | returns the number of a quadrature point from its local number on a face of the reference element |
| GetQuadNumbersBoundary | returns the numbers of quadrature points from local numbers on a face of the reference element |
| GetOffsetSh | returns offset for quadrature points on a face of the element |
| SetQuadNumbersBoundary | sets the numbers of quadrature points from local numbers on a face of the reference element |
| SetDofNumbersBoundary | sets the numbers of dof points from local numbers on a face of the reference element |
| GetTypeIntegrationEdge | returns the type of quadrature formula used for the unit interval |
| GetTypeIntegrationTriangle | returns the type of quadrature formula used for the unit triangle |
| GetTypeIntegrationQuadrangle | returns the type of quadrature formula used for the unit square |
| IsTangentialDof | returns true if the i-th dof is associated with a boundary of the element |
| WeightsND | returns the weight associated with a quadrature point |
| WeightsDofND | returns the weight associated with a dof point |
| GetFluxWeight | returns the half-weights associated with a boundary of the element |
| ComputeGaussIntegralSurfaceRef | computes integral over a boundary of the element of a function against basis functions with Gauss formulas |
| ApplyRhQuadratureTranspose | computation of the gradient (or curl) of the solution on quadrature points from values of the solution on quadrature points |
| ApplyRhQuadrature | transpose operation of ApplyRhQuadratureTranspose |
| ApplyRhBoundaryTranspose | computation of the gradient of the solution on quadrature points of the boundary |
| ApplyRhBoundary | transpose operation of ApplyRhBoundaryTranspose |
| ApplyShTranspose | computation of the value of the solution on quadrature points of a given face |
| ApplySh | transpose operation of ApplyShTranspose |
| ApplyShQuadratureTranspose | computation of the values of the solution on quadrature points of a given face from values of the solution on quadrature points |
| ApplyShQuadrature | transpose operation of ApplyShQuadratureTranspose |
| ApplyNablaShTranspose | computation of the gradient of the solution on quadrature points of a face |
| ApplyNablaSh | transpose operation of ApplyNablaShTranspose |
| ApplyNablaShQuadratureTranspose | computation of the gradient of the solution on quadrature points of a face from values of the solution on quadrature points |
| ApplyNablaShQuadrature | transpose operation of ApplyNablaShQuadratureTranspose |
| GetMemorySize | returns the size used by the object in bytes |
| SolveMassMatrix | overwrites x by solution of M y = x, where M is the mass matrix on reference element |
| SolveCholesky | overwrites x by solution of L y = x or LT y = x, where M = L LT is the mass matrix on reference element |
| MltMassMatrix | computes matrix-vector product y = M x, where M is the mass matrix on reference element |
| ComputeMassMatrix | computes the mass matrix for straight elements |
| IntegrateMassMatrix | computes the mass matrix for curved elements |
| PickNearDofs | retrieves dofs which are close to a given dof |
| ConstructNumberMap | completes numbering scheme |
| ApplyChTranspose | computation of the value of the solution on quadrature points |
| ApplyCh | transpose operation of ApplyChTranspose |
| ComputeProjectionDofRef | computes components of the solution u from values on points (usually related to degrees of freedom) |
| ComputeProjectionSurfaceDofRef | computes surface components of the solution u from values on points |
| ComputeIntegralRef | computes integral of a function against basis functions |
| ComputeIntegralSurfaceRef | computes integral over a boundary of the element of a function against basis functions |
Methods of ElementReference (inherited from ElementReference_Base, FiniteElementH1 and ElementGeomReferenceContainer)
In the table below, we list the methods of class ElementReference. This class is the base class for finite element and depends on the dimension and the type of finite element. For sake of simplicity, we have adjoined the methods from intermediary classes (ElementReference_Dim, ElementReferenceType and FaceReference/VolumeReference).
| GetTriangularSurfaceFiniteElement | returns the finite element class for a triangular face |
| GetQuadrangularSurfaceFiniteElement | returns the finite element class for a quadrilateral face |
| GetValuePhiOnQuadraturePoint | computes values of basis functions on a quadrature point |
| GetGradientPhiOnQuadraturePoint | computes gradient of basis functions on a quadrature point |
| GetCurlPhiOnQuadraturePoint | computes curl of basis functions on a quadrature point |
| GetDivPhiOnQuadraturePoint | computes divergence of basis functions on a quadrature point |
| GetValueSinglePhiQuadrature | computes values of a single basis function on all quadrature points |
| GetGradientSinglePhiQuadrature | computes values and gradients of a single basis function on all quadrature points |
| ComputeValuesPhiRef | computes basis functions on the reference element for a given point |
| ComputeGradientPhiRef | computes gradient of basis functions on the reference element for a given point |
| ComputeCurlPhiRef | computes curl of basis functions on the reference element for a given point |
| ComputeDivPhiRef | computes divergence of basis functions on the reference element for a given point |
| SetVariableOrder | initialization of projection on elements of different orders |
| ComputeValuesPhiQuadratureRef | computes basis functions associated with quadrature points on the reference element for a given point |
| FjSurfaceElem | Computes images of quadrature points of a face by the transformation Fi |
| DFjSurfaceElem | Computes jacobian matrices, normales and surface elements for quadrature points of a face |
| FjSurfaceElemDof | Computes images of dof points of a face by the transformation Fi |
| DFjSurfaceElemDof | Computes jacobian matrices, normales and surface elements for dof points of a face |
| GetLocalNumber | returns the number of a dof from its local number on a face of the reference element |
| GetNbDofBoundary | returns the number of dofs associated with a face of the element |
| PointsQuadInsideND | returns the quadrature points associated with volume integrals |
| GetSurfaceFiniteElement | returns the finite element for a face of the element |
| ProjectQuadratureToDofRef | projects a field on finite element basis from its values on quadrature points |
| ComputeLocalProlongationLowOrder | computes a local prolongation operator by considering a subdivided first-order mesh |
| ComputeNodalValuesRef | computes values on nodal points of the solution |
| ComputeProjectionPointsSurf | computes the projection from given points to another points (for a surface of the element) |
| ConstructFiniteElement | constructs the finite element class |
| ComputeVariableInterpolation | provides a list of orders for the finite element to compute interpolation |
| ComputeTriangularInterpolationProjectorOrder | computation of projection for triangular faces on elements of different orders |
| ComputeQuadrangularInterpolationProjectorOrder | computation of projection for quadrilateral faces on elements of different orders |
| ComputeIntegralGradientRef | computes integral of a function against gradient of basis functions |
| ComputeIntegralCurlRef | computes integral of a function against curl of basis functions |
| ComputeIntegralDivRef | computes integral of a function against divergence of basis functions |
| ComputeIntegralSurfaceGradientRef | computes integral over a boundary of the element of a function against gradient of basis functions |
| ComputeIntegralSurfaceCurlRef | computes integral over a boundary of the element of a function against curl of basis functions |
| ComputeIntegralSurfaceDivRef | computes integral over a boundary of the element of a function against divergence of basis functions |
| ComputeValueBoundaryRef | computes values of a solution on nodal points of a boundary, knowing only components of the solution on degrees of freedom |
| ComputeGradientBoundaryRef | computes gradient of a solution on nodal points of a boundary, knowing only components of the solution on degrees of freedom |
| ComputeCurlBoundaryRef | computes curl of a solution on nodal points of a boundary, knowing only components of the solution on degrees of freedom |
| ComputeDivBoundaryRef | computes divergence of a solution on nodal points of a boundary, knowing only components of the solution on degrees of freedom |
| ApplyRhTranspose | computation of the gradient (or curl) of the solution on quadrature points |
| ApplyRh | transpose operation of ApplyRhTranspose |
| ApplyRhSplit | splits the results of ApplyRh in several vectors |
| ApplyRhQuadratureSplit | splits the results of ApplyRhQuadrature in several vectors |
| ApplyConstantRh | matrix vector product y = R x, where R = ∫ ∇ φj φi |
| ApplyConstantRhTranspose | matrix vector product y = RT x, where R = ∫ ∇ φj φi |
| ApplyConstantRhSplit | matrix vector product y = R x, the result is split into several vectors |
| AddConstantMassMatrix | adds the mass matrix to a given matrix |
| AddVariableMassMatrix | adds the mass matrix with a variable weight function to a given matrix |
| AddConstantElemMatrix | adds an elementary matrix (with uniform weight) matrix to a given matrix |
| AddVariableElemMatrix | adds an elementary matrix with variable coefficients to a given matrix |
| AddConstantStiffnessMatrix | adds the stiffness matrix to a given matrix |
| AddVariableStiffnessMatrix | adds the stiffness matrix with a variable weight function to a given matrix |
| FindH1RotationTri | computes new dof numbers after a rotation of a triangular face (scalar elements) |
| FindHcurlRotationTri | computes new dof numbers after a rotation of a triangular face (edge elements) |
| FindHcurlRotationQuad | computes new dof numbers after a rotation of a quadrangular face (edge elements) |
| FindHdivRotationTri | computes new dof numbers after a rotation of a triangular face (facet elements) |
| FindHdivRotationQuad | computes new dof numbers after a rotation of a quadrangular face (facet elements) |
Methods of ElementGeomReference (inherited from ElementGeomReference_Base)
The class ElementGeomReference is the base class for geometric finite elements (such as TriangleGeomReference, QuadrangleGeomReference).
| PointsQuadInsideND | returns the quadrature points associated with volume integrals |
| GetNbPointsNodalElt | returns the number of nodal points in the element |
| GetNbNodalBoundary | returns the number of nodal points on a face of the element |
| GetNumNodes2D/GetNumNodes3D | returns the number of a node from its position (i, j, k) on the reference element |
| GetCoordinateNodes2D/GetCoordinateNodes3D | returns the position (i, j, k) of a node on the reference element |
| PointsNodalBoundary | returns coordinates of a nodal point of a face |
| GetNodalNumber | returns the number of a node from its local number on a face of the reference element |
| PointsND | returns coordinates of a quadrature point |
| PointsQuadND | returns inside quadrature points + boundary quadrature points |
| WeightsND | returns weight of a quadrature point |
| PointsDofBoundary | returns dof points of a face |
| PointsQuadratureBoundary | returns a quadrature point of a face |
| WeightsQuadratureBoundary | returns a quadrature weight of a face |
| GetNbPointsDof | returns the number of dof points on the element |
| PointsDofND | returns coordinates of a dof point |
| GetNbPointsQuadrature | returns the number of quadrature points in the element |
| GetNbQuadBoundary | returns the number of quadrature points on a face of the element |
| GetLocalCoordOnBoundary | returns coordinates of a point on the reference element from its local coordinates on the face |
| GetCurvatureNodal | computes curvatures for 2-D elements |
| GetBoundingBox | computes a polyhedron bounding the element |
| IsAffineTransformation | returns true if the transformation Fi is affine |
| IsLocalFaceQuadrilateral | returns true if a face of the reference element is a quadrilateral |
| TangenteLocX/TangenteLocY | returns tangent vectors of a face of the reference element |
| GetTangentialVector | returns a 3-D tangential vector of a face from its components on the 2-D square/triangle |
| TransposeTangentialVector | returns the 2-D vector (on the square/triangle) from the 3-D tangential vector of a face |
Methods for the classes FiniteElementH1, FiniteElementHcurl or FiniteElementHdiv
These classes link the computations on the reference element with computations on the real element. Methods listed previously (in ElementReference or ElementReference_Base) apply to the reference element (except ComputeNodalGradient), their names end often with Ref. The methods listed below apply to the real element. They call methods of the reference element, and apply the Piola transform to obtain the result on the real element.
| ComputeValuesPhi | computes values of basis functions on a given point |
| ComputeValuesGradientPhi | computes gradient (or curl) of basis functions on a given point |
| GetCurlFromGradient | computes the curl from gradient for edge elements |
| ComputeValuesPhiBoundary | computes the values of basis functions on quadrature points of the face of an element |
| ComputeValuesGradientPhiBoundary | computes the gradient of basis functions on quadrature points of the face of an element |
| ComputeNodalValues | computes values of solution on nodal points from its components on degrees of freedom |
| ComputeQuadratureValues | computes values of solution on quadrature points from its components on degrees of freedom |
| ComputeProjectionDof | computes components of a function on the basis functions |
| ComputeProjectionSurfaceDof | computes components of a function on the basis functions (only on a face of the element) |
| ComputeIntegral | computes the integral of a function against basis functions |
| ComputeIntegralGradient | computes the integral of a function against gradient (or curl) of basis functions |
| ComputeGaussIntegralSurface | computes the surface integral of a function against basis functions with Gauss formulas |
| ComputeIntegralSurface | computes the surface integral of a function against basis functions |
| ComputeIntegralSurfaceGradient | computes the surface integral of a function against gradient (or curl) of basis functions |
| ComputeValueBoundary | computes the values of the solution on nodal points of a face from its components on degrees of freedom |
| ComputeGradientBoundary | computes the gradient (or curl) of the solution on nodal points of a face from its components on degrees of freedom |
| ComputeValueNodalBoundary | extracts values of the solution on nodal points of a face from values on all the nodal points |
| ComputeLocalProlongation | computes prolongation operator between low order and high order finite elements |
| ApplyRotationCyclic | applies rotation to vector-valued solution for cyclic domain (only for edge elements) |
| ApplyInverseRotationCyclic | applies inverse rotation to vector-valued solution for cyclic domain (only for edge elements) |
GetGeometryOrder
Syntax
| int GetGeometryOrder() const |
This method returns the order of approximation r used for the geometric finite element.
Example :
TriangleGeomReference tri; int order = 4; tri.ConstructFiniteElement(order); // should give r = 4 int r = tri.GetGeometryOrder();
Related topics :
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
NormaleLoc
Syntax
| R_N NormaleLoc(int num_loc) const |
This method returns the outward normale for the face num_loc of the reference element. For example, for the unit cube, the outward normale is (-1, 0, 0) if num_loc is equal to 0.
Example :
TriangleGeomReference tri; int order = 4; tri.ConstructFiniteElement(order); // outward normale for an edge of the triangle ? R2 normale = tri.NormaleLoc(1); // 3-D case : PyramidGeomReference pyr; pyr.ConstructFiniteElement(order); R3 n = pyr.NormaleLoc(2);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
PointsNodal1D
Syntax
| Real_wp PointsNodal1D(int i) const |
| const VectReal_wp& PointsNodal1D() const |
This method returns the 1-D nodal points on the unit interval [0, 1] used by the finite element. In the first syntax, you can retrieve a single nodal point. Most of the times, these nodal points should coincide with Gauss-Lobatto points.
Example :
TriangleGeomReference tri; int order = 4; tri.ConstructFiniteElement(order); // a single nodal point int i = 2; Real_wp x = tri.PointsNodal1D(i); // or all 1-D nodal points const VectReal_wp& xvec = tri.PointsNodal1D();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
PointsNodalND
Syntax
| R_N PointsNodalND(int i) const |
| const VectR_N& PointsNodalND() const |
This method returns the nodal points on the reference element used by the finite element. In the first syntax, you can retrieve a single nodal point.
Example :
TriangleGeomReference tri; int order = 4; tri.ConstructFiniteElement(order); // a single nodal point of the unit triangle int i = 5; R2 x = tri.PointsNodalND(i); // or all nodal points const VectR2& xvec = tri.PointsNodalND(); // for 3-D elements : PyramidGeomReference pyr; pyr.ConstructFiniteElement(order); const VectR3& pts = pyr.PointsNodalND();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
WeightsNodalND
Syntax
| Real_wp WeightsNodalND(int i) const |
| const VectReal_wp& WeightsNodalND() const |
This method returns the weight associated with nodal points of the reference element. In the first syntax, you can retrieve a single weight. This method is relevant only for quadrilaterals and hexahedra for which nodal points coincide with quadrature points.
Example :
QuadrangleGeomReference quad; int order = 4; quad.ConstructFiniteElement(order); // a single nodal point of the unit square int i = 5; R2 x = quad.PointsNodalND(i); Real_wp w = quad.WeightsNodalND(i); // and weight // or all nodal points const VectR2& xvec = quad.PointsNodalND(); const VectReal_wp& weights = quad.WeightsNodalND(); // and weights
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
PointsDof1D
Syntax
| Real_wp PointsDof1D(int i) const |
| const VectReal_wp& PointsDof1D() const |
This method returns the 1-D points on the unit interval [0, 1] associated with the degrees of freedom (dof). In the first syntax, you can retrieve a single dof point. The degrees of freedoms on the edges will be spaced following these dof points.
Example :
TriangleClassical tri; int order = 4; tri.ConstructFiniteElement(order); // a single dof point (on unit interval) int i = 2; Real_wp x = tri.PointsDof1D(i); // or all 1-D dof points const VectReal_wp& xvec = tri.PointsDof1D();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
Points1D
Syntax
| Real_wp Points1D(int i) const |
| const VectReal_wp& Points1D() const |
This method returns the 1-D integration points on the unit interval [0, 1]. In the first syntax, you can retrieve a single integration point. For quadrilaterals and hexahedra, quadrature points of the reference element will be generated by a tensorization of these 1-D points.
Example :
QuadrangleGauss quad; int order = 4; quad.ConstructFiniteElement(order); // a single integration point (on unit interval) int i = 2; Real_wp x = quad.Points1D(i); // or all 1-D integration points const VectReal_wp& xvec = quad.Points1D();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
Weights1D
Syntax
| Real_wp Weights1D(int i) const |
| const VectReal_wp& Weights1D() const |
This method returns the 1-D integration weights on the unit interval [0, 1]. In the first syntax, you can retrieve a single integration weight. For quadrilaterals and hexahedra, quadrature points and weights of the reference element will be generated by a tensorization of these 1-D points and weights.
Example :
QuadrangleGauss quad; int order = 4; quad.ConstructFiniteElement(order); // a single integration weight (on unit interval) int i = 2; Real_wp x = quad.Weights1D(i); // or all 1-D integration weights const VectReal_wp& xvec = quad.Weights1D();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
GetHybridType
Syntax
| int GetHybridType() const |
This method returns 0 if the element is a triangle and 1 if the element is a quadrangle. In 3-D, it returns 0 for a tetrahedron, 1 for a pyramid, 2 for a wedge and 3 for an hexahedron.
Example :
QuadrangleGauss quad; int order = 4; quad.ConstructFiniteElement(order); // should return 1 here (quad) int type = quad.GetHybridType();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
GetNbVertices
Syntax
| int GetNbVertices() const |
This method returns the number of vertices of the reference element (for example 4 for the unit square).
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // should return 5 here (a pyramid has 5 vertices) int nb_vertices = pyr.GetNbVertices();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
GetNbEdges
Syntax
| int GetNbEdges() const |
This method returns the number of edges of the reference element (for example 4 for the unit square).
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // should return 8 here (a pyramid has 8 edges) int nb_edges = pyr.GetNbEdges();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
GetNbBoundaries
Syntax
| int GetNbBoundaries() const |
This method returns the number of edges of the reference element in 2-D, and the number of faces in 3-D.
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // should return 5 here (a pyramid has 5 faces) int nb_edges = pyr.GetNbBoundaries(); TriangleClassical tri; tri.ConstructFiniteElement(order); nb_vertices = tri.GetNbBoundaries(); // 3 edges
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
SetAxisymmetricGeometry
Syntax
| void SetAxisymmetricGeometry() |
This method informs that the 2-D mesh is actually a section of an axisymmetric domain. This information is relevant for the computation of the curvatures, since there is a curvature due to the rotation of the section.
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); pyr.SetAxisymmetricGeometry();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
GetSurfaceFiniteElement
Syntax
| const Element& GetSurfaceFiniteElement(int num_loc) |
This method returns the 1-D finite element that corresponds to the restriction of 2-D basis functions on an edge of the element. For a 3-D element, it will return the 2-D finite element that corresponds to the restriction of the 3-D finite element on a face. num_loc is the local edge number (local face number in 3-D).
Example :
WedgeGeomReference wed; wed.ConstructFiniteElement(3); // face 0 is a quadrangle => we get a quadrilateral finite element const ElementGeomReference<Dimension2>& quad = wed.GetSurfaceFiniteElement(0); PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // face 1 is a triangle, it should return a triangular finite element const ElementReference<Dimension2, 1>& tri = pyr.GetSurfaceFiniteElement(1);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
SetMesh
Syntax
| void SetMesh(const Mesh& mesh) |
This method takes the mesh that will be used to compute transformation Fi. Usually, this method has to be called after ConstructFiniteElement in order to initialize arrays needed for the transformation Fi (for curved elements).
Example :
// starting with a curved mesh
Mesh<Dimension3> mesh;
mesh.SetGeometryOrder(2);
mesh.Read("test.msh");
WedgeClassical wed;
wed.ConstructFiniteElement(3);
wed.SetMesh(mesh);
// then you can compute transformation Fi
SetPoints<Dimension3> pts;
VectR3 s; int num_elem = 40;
mesh.GetVerticesElement(num_elem, s);
wed.FjElem(s, pts, mesh, num_elem);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
GetNormale
Syntax
| void GetNormale(const MatrixN_N& dfi_m1, R_N& normale, Real_wp& dsi, int num_loc) |
This method computes the outgoing normale ni to the real element Ki from the inverse of the jacobian matrix DFi and the normale
 on the reference element. The used formula is the following one
on the reference element. The used formula is the following one
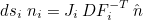
where Ji is the determinant of DFi and dsi the surface element (used for boundary integrals).
Parameters
- dfi_m1 (in)
- matrix DFi-1
- normale (out)
- outgoing normale to the selected face
- dsi (out)
- surface element to use for a boundary integral on the selected face
- num_loc (in)
- local face number (edge number in 2-D)
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // then jacobian matrix on a single point of a face Matrix3_3 dfjm1; wed.DFj(s, pts, R3(0.4, 0.7, 0.0), dfjm1, mesh, num_elem); GetInverse(dfjm1); // from this jacobian matrix, you can deduce the outgoing normale associated with this point // and surface element R3 normale; Real_wp dsj; wed.GetNormale(dfjm1, normale, dsj, 0); cout << "Normale = " << normale;
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
FjCurvePhi
Syntax
| void FjCurvePhi(const SetPoints& PointsElem, const R_N& pt_loc, R_N& pt_glob, VectReal_wp& phi) |
This method computes pt_glob = Fi(pt_loc) for a curved element. It also computes the shape functions φk involved in the computation. For curved elements the transformation Fi is given as
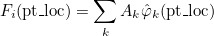
The points Ak are provided in the object PointsElem whereas the coefficients φk are stored in the output array phi.
Parameters
- PointsElem (in)
- object storing nodal points Ak of the element
- pt_loc (in)
- local point on the reference element
- pt_glob (out)
- point on the real element
- phi (out)
- shape functions evaluated at pt_loc
Example :
WedgeGeomReference wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // we compute res = Fi(pt_loc) and shape functions phi_i(pt_loc) R3 pt_loc(0.2, 0.5, 0.1); VectReal_wp phi; R3 res; wed.FjCurvePhi(pts, pt_loc, res, phi); SetMatrices<Dimension3> mat; wed.DFjElemNodal(s, pts, mat, mesh, num_elem); // then we can reuse the shape function to compute jacobian matrix Matrix3_3 dfj; wed.DFjCurvePhi(mat, pt_loc, dfj, phi);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
DFjCurvePhi
Syntax
| void DFjCurvePhi(const SetMatrices& MatricesElem, const R_N& pt_loc, MatrixN_N& dfj, const VectReal_wp& phi) |
This method computes pt_glob = DFi(pt_loc) for a curved element, from the shape functions φk (already computed by the method FjCurvePhi). The computation is performed with the relation
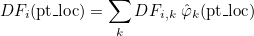
The matrices DFi, k are provided in the object MatricesElem whereas the coefficients φk are given in the array phi.
Parameters
- MatricesElem (in)
- object storing jacobian matrices DFi, k on nodal points
- pt_loc (in)
- local point on the reference element
- dfj (out)
- jacobian matrix DFi at pt_loc
- phi (in)
- shape functions evaluated at pt_loc
Example :
WedgeGeomReference wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // we compute res = Fi(pt_loc) and shape functions phi_i(pt_loc) R3 pt_loc(0.2, 0.5, 0.1); VectReal_wp phi; R3 res; wed.FjCurvePhi(pts, pt_loc, res, phi); SetMatrices<Dimension3> mat; wed.DFjElemNodal(s, pts, mat, mesh, num_elem); // then we can reuse the shape function to compute jacobian matrix Matrix3_3 dfj; wed.DFjCurvePhi(mat, pt_loc, dfj, phi);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
GetMemorySize
Syntax
| size_t GetMemorySize() const |
This method returns the size used by the finite element in bytes.
Example :
TriangleClassical tri; tri.ConstructFiniteElement(5); cout << "Size = " << tri.GetMemorySize() << endl;
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
GetCenterReferenceElement
Syntax
| R_N GetCenterReferenceElement() const |
This method returns the center of the reference element (e.g. (0.5, 0.5) for the unit square).
Example :
TriangleGeomReference tri; tri.ConstructFiniteElement(5); cout << "Center of unit triangle = " << tri.GetCenterReferenceElement() << endl;
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ConstructFiniteElement
Syntax
| void ConstructFiniteElement(int order) |
This method constructs a finite element at a given order.
Example :
TriangleGeomReference tri; tri.ConstructFiniteElement(5); // then you can for example compute values of shape functions on a point R2 pt_loc(0.2, 0.3); VectReal_wp phi; tri.ComputeValuesPhiNodalRef(pt_loc, phi);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ConstructFiniteElement
Syntax
| void ConstructFiniteElement(int order, int rgeom, int rquad, int type_quad, int r_edge, int type_int_edge) |
| void ConstructFiniteElement(int order, int rgeom, int rquad, int type_quad, int r_tri, int r_quad, int type_int_tri, int type_int_quad, int gauss_z) |
This method constructs a finite element at a given order. Only the first argument is needed, other arguments are optional. The first syntax is defined for 2-D finite elements, whereas the second syntax applies for 3-D finite elements.
Parameters
- order (in)
- order of approximation for the finite element space
- rgeom (optional)
- order of approximation for shape functions (geometry)
- rquad (optional)
- order for quadrature rules
- type_quad (optional)
- type of integration rule to use
- r_edge (optional)
- order for integration over edges (in 2-D)
- type_int_edge (optional)
- type of integration over edges (in 2-D)
- r_tri (optional)
- order for integration over triangles (in 3-D)
- type_int_tri (optional)
- type of integration over triangles (in 3-D)
- r_quad (optional)
- order for integration over quadrangles (in 3-D)
- type_int_quad (optional)
- type of integration over quadrangles (in 3-D)
- gauss_z (optional)
- type of integration to use in z-coordinate (for pyramids only)
Example :
TriangleClassical tri; tri.ConstructFiniteElement(5); // you can specify optional parameters tri.ConstructFiniteElement(3, 2, 4); // P3 element, second order for geometry, and fourth order for integration
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
GetNewNodalInterpolation
Syntax
| FiniteElementProjector* GetNewNodalInterpolation() const |
This method returns a new projector (class that derives from FiniteElementProjector) that can be used to compute the interpolation from nodal points to other points.
Example :
TriangleGeomReference tri; tri.ConstructFiniteElement(5); // we create the object with GetNewNodalInterpolation FiniteElementProjector* proj; proj = tri.GetNewNodalInterpolation(); // then we can compute the projector with Init VectR2 other_points(3); other_points(0).Init(0.2, 0.2); // etc proj->Init(tri, other_points); // ProjectScalar to compute the projection of a field from nodal points to the other points VectReal_wp u_nodal(tri.GetNbPointsNodalElt()); u_nodal.FillRand(); VectReal_wp u_other(other_points.GetM()); proj->ProjectScalar(u_nodal, u_other);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
Fj
Syntax
| void Fj(const VectR_N& s, const SetPoints& PointsElem, const R_N& pt_loc, R_N& pt_glob, const Mesh& mesh, int num_elem) |
This method computes pt_glob = Fi(pt_loc).
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object storing nodal points of the element
- pt_loc (in)
- local point on the reference element
- pt_glob (out)
- point on the real element
- mesh (in)
- input mesh
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh; HexahedronLobatto hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); hex.FjElemNodal(s, pts, mesh, num_elem); // we compute res = Fi(pt_loc) R3 pt_loc(0.2, 0.5, 0.1); R3 res; hex.Fj(s, pts, pt_loc, res, mesh, num_elem);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
DFj
Syntax
| void DFj(const VectR_N& s, const SetPoints& PointsElem, const R_N& pt_loc, MatrixN_N& dfj, const Mesh& mesh, int num_elem) |
This method computes the jacobian matrix DFi(pt_loc).
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object storing nodal points of the element
- pt_loc (in)
- local point on the reference element
- dfj (out)
- jacobian matrix evaluated at pt_loc
- mesh (in)
- input mesh
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh; HexahedronLobatto hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); hex.FjElemNodal(s, pts, mesh, num_elem); // we compute res = Fi(pt_loc) R3 pt_loc(0.2, 0.5, 0.1); R3 res; hex.Fj(s, pts, pt_loc, res, mesh, num_elem); // and jacobian matrix dfj = DFi(pt_loc) Matrix3_3 dfj; hex.DFj(s, pts, pt_loc, dfj, mesh, num_elem);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
FjLinear
Syntax
| void FjLinear(const VectR_N& s, const R_N& pt_loc, R_N& pt_glob) |
This method computes pt_glob = Fi(pt_loc) assuming that the element is not curved. The transformation Fi is linear for triangles/tetrahedra (but bilinear for quadrilaterals).
Parameters
- s (in)
- vertices of the element
- pt_loc (in)
- local point on the reference element
- pt_glob (out)
- point on the real element
Example :
Mesh<Dimension3> mesh; HexahedronLobatto hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // vertices of the element VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); // we compute res = Fi(pt_loc) (if the element is straight) R3 pt_loc(0.2, 0.5, 0.1); R3 res; hex.FjLinear(s, pt_loc, res);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
DFjLinear
Syntax
| void DFjLinear(const VectR_N& s, const R_N& pt_loc, MatrixN_N& dfj) |
This method computes the jacobian matrix DFi(pt_loc) assuming that the element is not curved. The transformation Fi is linear for triangles/tetrahedra (but bilinear for quadrilaterals).
Parameters
- s (in)
- vertices of the element
- pt_loc (in)
- local point on the reference element
- dfj (out)
- jacobian matrix evaluated at pt_loc
Example :
Mesh<Dimension3> mesh; HexahedronLobatto hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // vertices of the element VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); // we compute res = Fi(pt_loc) for a straight element R3 pt_loc(0.2, 0.5, 0.1); R3 res; hex.FjLinear(s, pt_loc, res); // and jacobian matrix dfj = DFi(pt_loc) Matrix3_3 dfj; hex.DFjLinear(s, pt_loc, dfj);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
GetMinimalSize
Syntax
| Real_wp GetMinimalSize(const VectR_N& s) const |
This method computes the minimal length of edges of the element. It takes the list of vertices as argument.
Example :
Mesh<Dimension3> mesh; HexahedronGeomReference hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // vertices of the element VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); // minimal size of element Real_wp h = hex.GetMinimalSize(s);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
OutsideReferenceElement
Syntax
| bool OutsideReferenceElement(const VectR_N& s, const R_N& pt_loc, const Real_wp& epsilon) const |
This method returns true if the point pt_loc is outside the reference element. The parameter epsilon is a threshold such that a point slightly outside from the reference element will be considered inside it.
Example :
Mesh<Dimension3> mesh; HexahedronGeomReference hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // vertices of the element VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); // pt_loc is outside the reference element ? R3 pt_loc(-1e-12, 0.1, 0.05); bool outside = hex.OutsideReferenceElement(s, pt_loc, 1e-10); if (outside) cout << "The point is outside the reference element" << endl;
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
GetDistanceToBoundary
Syntax
| Real_wp GetDistanceToBoundary(const R_N& pt_loc) const |
| Real_wp GetDistanceToBoundary(const R_N& pt_loc, int num_loc) const |
This method returns the distance of the point pt_loc to the boundary of the reference element. If the point is outside the reference element, it will return a negative distance. In the second syntax, the method returns the distance to a specific boundary of the element. For this syntax, the returned distance is always positive.
Example :
Mesh<Dimension3> mesh; HexahedronGeomReference hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // distance of pt_loc to the boundary of unit cube ? R3 pt_loc(0.001, 0.1, 0.05); Real_wp dist = hex.GetDistanceToBoundary(pt_loc); // should return 0.001 // distance to the face 1 of unit cube (i.e. y = 0) dist = hex.GetDistanceToBoundary(pt_loc, 1); // should return 0.1
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ProjectPointOnBoundary
Syntax
| void ProjectPointOnBoundary(R_N& pt_loc) const |
This method projects the point pt_loc to the boundary of the reference element if the point is outside the reference element. If the point is inside the reference element, the point is not modified.
Example :
Mesh<Dimension3> mesh; HexahedronGeomReference hex; hex.ConstructFiniteElement(3); hex.SetMesh(mesh); // projection of pt_loc to the boundary of unit cube R3 pt_loc(-0.001, 0.1, 0.05); hex.ProjectPointOnBoundary(pt_loc); // pt_loc should be equal to (0, 0.1, 0.05)
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ComputeCoefJacobian
Syntax
| void ComputeCoefJacobian(const VectR_N& s, VectReal_wp& coef) const |
This method computes the coefficients of the polynomial describing the determinant of jacobian matrix. It is implemented only for the tetrahedron, pyramid and wedge. This determinant can be written for straight elements as:
- Tetrahedron : det(DFi) = c0
- Pyramid : det(DFi) = c0 + c1 x + c2 y + 2 c3 x y
- Wedge : det(DFi) = c0 + c1 x(1-y) + c2 y + c3 z + c4 x(1-y)z + c5 y z + c6 z2
For pyramids, x, y, z are the coordinates on the unit cube (and not on the symmetric pyramid).
Example :
Mesh<Dimension3> mesh; PyramidGeomReference pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // vertices of the element VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); // polynomial coefficients of J_i = det(DF_i) VectReal_wp coef; pyr.ComputeCoefJacobian(s, coef);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
FjElem
Syntax
| void FjElem(const VectR_N& s, SetPoints& PointsElem, const Mesh& mesh, int num_elem) |
This method computes the transformation Fi(x) for all the predefined points (i.e. nodal, quadrature and dof points) of the element. The computed points are stored in the object PointsElem. If you need to compute only quadrature points (resp. nodal points or dof points) you can call FjElemQuadrature (resp. FjElemNodal or FjElemDof), it will be more efficient. If two of more sets of points are needed, it is better to call FjElem that will compute all the points.
Parameters
- s (in)
- vertices of the element
- PointsElem (out)
- object that will store the computed points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for all points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElem(s, pts, mesh, num_elem); // if you want to retrieve a nodal point R3 pt_glob = pts.GetPointNodal(4); // or a quadrature point pt_glob = pts.GetPointQuadrature(11); // or a dof point pt_glob = pts.GetPointDof(7);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
FjElemNodal
Syntax
| void FjElemNodal(const VectR_N& s, SetPoints& PointsElem, const Mesh& mesh, int num_elem) |
This method computes the transformation Fi(x) for all the nodal points of the element. The computed points are stored in the object PointsElem.
Parameters
- s (in)
- vertices of the element
- PointsElem (out)
- object that will store the computed nodal points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // if you want to retrieve a nodal point R3 pt_glob = pts.GetPointNodal(4);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
FjElemQuadrature
Syntax
| void FjElemQuadrature(const VectR_N& s, SetPoints& PointsElem, const Mesh& mesh, int num_elem) |
This method computes the transformation Fi(x) for all the quadrature points of the element. The computed points are stored in the object PointsElem.
Parameters
- s (in)
- vertices of the element
- PointsElem (out)
- object that will store the computed quadrature points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // if you want to retrieve a quadrature point R3 pt_glob = pts.GetPointQuadrature(4);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
FjElemDof
Syntax
| void FjElemDof(const VectR_N& s, SetPoints& PointsElem, const Mesh& mesh, int num_elem) |
This method computes the transformation Fi(x) for all the dof points of the element. Dof points are the points associated with the degrees of freedom. These points are used when a field needs to be projected on the basis functions. The computed points are stored in the object PointsElem.
Parameters
- s (in)
- vertices of the element
- PointsElem (out)
- object that will store the computed dof points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for dof points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemDof(s, pts, mesh, num_elem); // if you want to retrieve a dof point R3 pt_glob = pts.GetPointDof(4);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
DFjElem
Syntax
| void DFjElem(const VectR_N& s, const SetPoints& PointsElem, SetMatrices& MatricesElem, const Mesh& mesh, int num_elem) |
This method computes the jacobian matrix of the transformation Fi for all the predefined points (i.e. nodal, quadrature and dof points) of the element. The computed matrices are stored in the object MatricesElem.
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object containing the nodal points
- MatricesElem (out)
- object that will store the computed matrices
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // then you can compute jacobian matrices for all points SetMatrices<Dimension3> mat; wed.DFjElem(s, pts, mat, mesh, num_elem); // if you want to retrieve the jacobian matrix on a nodal point Matrix3_3 dfj = mat.GetPointNodal(4); // or on a quadrature point dfj = mat.GetPointQuadrature(11); // or on a dof point dfj = mat.GetPointDof(7);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
DFjElemNodal
Syntax
| void DFjElemNodal(const VectR_N& s, const SetPoints& PointsElem, SetMatrices& MatricesElem, const Mesh& mesh, int num_elem) |
This method computes the jacobian matrix of the transformation Fi for all the nodal points of the element. The computed matrices are stored in the object MatricesElem.
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object containing the nodal points
- MatricesElem (out)
- object that will store the computed matrices on nodal points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // then you can compute jacobian matrices for nodal points SetMatrices<Dimension3> mat; wed.DFjElemNodal(s, pts, mat, mesh, num_elem); // if you want to retrieve the jacobian matrix on a nodal point Matrix3_3 dfj = mat.GetPointNodal(4);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
DFjElemQuadrature
Syntax
| void DFjElemQuadrature(const VectR_N& s, const SetPoints& PointsElem, SetMatrices& MatricesElem, const Mesh& mesh, int num_elem) |
This method computes the jacobian matrix of the transformation Fi for all the quadrature points of the element. The computed matrices are stored in the object MatricesElem.
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object containing the nodal points
- MatricesElem (out)
- object that will store the computed matrices on quadrature points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // then you can compute jacobian matrices for quadrature points SetMatrices<Dimension3> mat; wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // if you want to retrieve the jacobian matrix on a quadrature point Matrix3_3 dfj = mat.GetPointQuadrature(4);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
DFjElemDof
Syntax
| void DFjElemDof(const VectR_N& s, const SetPoints& PointsElem, SetMatrices& MatricesElem, const Mesh& mesh, int num_elem) |
This method computes the jacobian matrix of the transformation Fi for all the dof points of the element. The computed matrices are stored in the object MatricesElem.
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object containing the nodal points
- MatricesElem (out)
- object that will store the computed matrices on dof points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // then you can compute jacobian matrices for dof points SetMatrices<Dimension3> mat; wed.DFjElemDof(s, pts, mat, mesh, num_elem); // if you want to retrieve the jacobian matrix on a dof point Matrix3_3 dfj = mat.GetPointDof(4);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ComputeValuesNodalPhi1D
Syntax
| void ComputeValuesNodalPhi1D(const Real_wp& x, const VectReal_wp& phi) |
This method computes the 1-D shape functions (on the unit interval) for a given point. These shape functions are Lagrange polynomial given as.
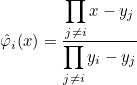
where yi are nodal points on the unit interval (usually Gauss-Lobatto points).
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // if you want to compute phi_i for a given point // where phi_i are 1-D shape functions Real_wp x(0.23); VectReal_wp phi; wed.ComputeValuesNodalPhi1D(x, phi);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ComputeValuesPhiNodalRef
Syntax
| void ComputeValuesPhiNodalRef(const R_N& pt, const VectReal_wp& phi) |
This method computes the shape functions (on the reference element) for a given point. These shape functions are interpolatory functions based on nodal points, they satisfy:
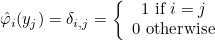
where yi are nodal points on the reference element.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // if you want to compute phi_i for a given point // where phi_i are shape functions R3 x(0.23, 0.3, 0.1); VectReal_wp phi; pyr.ComputeValuesPhiNodalRef(x, phi);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ComputeGradientPhiNodalRef
Syntax
| void ComputeGradientPhiNodalRef(const R_N& pt, const VectR_N& grad_phi) |
This method computes the gradient of shape functions (on the reference element) for a given point. These shape functions are interpolatory functions based on nodal points, they satisfy:
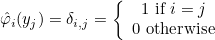
where yi are nodal points on the reference element.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // if you want to compute phi_i for a given point // where phi_i are shape functions R3 x(0.23, 0.3, 0.1); VectReal_wp phi; wed.ComputeValuesPhiNodalRef(x, phi); // and gradients : VectR3 grad_phi; pyr.ComputeGradientPhiNodalRef(x, grad_phi);
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ComputeCoefficientTransformation
Syntax
| void ComputeCoefficientTransformation() |
This method computes the coefficients needed to evaluate the transformation Fi on predefined points. Usually, it is not needed to call this function since it is already called in ConstructFiniteElement.
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ComputeNodalGradientRef
Syntax
| void ComputeNodalGradientRef(const Vector& u, VectR_N& grad_u) const |
This method computes the gradient of a field u (defined on the reference element). On input, the vector u stores the values of the field on nodal points:
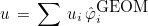
where
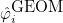 are shape functions based on nodal points. On output the vector grad_u stores the values of ∇ u on nodal points:
are shape functions based on nodal points. On output the vector grad_u stores the values of ∇ u on nodal points:
The computations are made on the reference element. If you need to compute a gradient on the real element, you can call ComputeNodalGradient. The method works for real-valued vectors or complex-valued vectors.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // defining a field on the reference element VectReal_wp u(pyr.GetNbPointsNodalElt()); u.FillRand(); // u(i) is the value of u on the nodal point i // computing its gradient VectR3 grad_u; pyr.ComputeNodalGradientRef(u, grad_u); // grad_u(i) is the gradient of u on the nodal point i
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
ComputeNodalGradient
Syntax
| void ComputeNodalGradient(const SetMatrices& MatricesElem, const Vector& u, VectR_N& grad_u) const |
This method computes the gradient of a field u (defined on the real element). On input, the vector u stores the values of the field on nodal points:
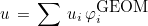
where
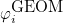 are shape functions based on nodal points. On output the vector grad_u stores the values of ∇ u on nodal points:
are shape functions based on nodal points. On output the vector grad_u stores the values of ∇ u on nodal points:
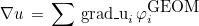
The computations are made on the real element. That is the reason why jacobian matrices are needed in MatricesElem. The method works for real-valued vectors or complex-valued vectors.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // then you can compute jacobian matrices for nodal points SetMatrices<Dimension3> mat; wed.DFjElemNodal(s, pts, mat, mesh, num_elem); // defining a field on the real element VectReal_wp u(pyr.GetNbPointsNodalElt()); u.FillRand(); // u(i) is the value of u on the nodal point i // computing its gradient VectR3 grad_u; pyr.ComputeNodalGradient(mat, u, grad_u); // grad_u(i) is the gradient of u on the nodal point i
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReference.cxx
QuadratureEqualNodal
Syntax
| bool QuadratureEqualNodal() const |
This method returns true if the quadrature points coincide with nodal points.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); // nodal points = quadrature points ? if (pyr.QuadratureEqualNodal()) cout << "Quadrature points are equal to nodal points" << endl;
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
DofEqualNodal
Syntax
| bool DofEqualNodal() const |
This method returns true if the dof points coincide with nodal points.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); // nodal points = dof points ? if (pyr.DofEqualNodal()) cout << "Dof points are equal to nodal points" << endl;
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
DofEqualQuadrature
Syntax
| bool DofEqualQuadrature() const |
This method returns true if the dof points coincide with quadrature points.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); // dof points = quadrature points ? if (pyr.DofEqualQuadrature()) cout << "Quadrature points are equal to dof points" << endl;
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
SetGeometryOrder
Syntax
| void SetGeometryOrder(int order) |
This method modifies the geometry order stored in the geometric element. On a regular use, this method should not be called since the geometry order is set when ConstructFiniteElement is called.
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
GetGeometricElement
Syntax
| const ElementGeomReference& GetGeometricElement() const |
This method returns the geometric element stored in the finite element class. The geometric element is an object used to store shape functions and compute transformation Fi.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); // to retrieve the geometric element : const ElementGeomReference<Dimension3>& elt = pyr.GetGeometricElement();
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
SetPointsDof1D
Syntax
| void SetPointsDof1D(const VectReal_wp& pts) |
This method sets the 1-D dof points stored in the geometric element. This method does not need to be called in a regular use.
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
SetPoints1D
Syntax
| void SetPoints1D(const VectReal_wp& pts) |
This method sets the 1-D quadrature points stored in the geometric element. This method does not need to be called in a regular use.
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
SetWeights1D
Syntax
| void SetWeights1D(const VectReal_wp& poids) |
This method sets the 1-D quadrature weights stored in the geometric element. This method does not need to be called in a regular use.
Location :
FiniteElement/ElementGeomReference.hxx
FiniteElement/ElementGeomReferenceInline.cxx
LumpedMassMatrix
Syntax
| bool LumpedMassMatrix() const |
This method returns true if the finite element class achieves mass lumping. For instance, it is achieved by using Gauss-Lobatto points both for degrees of freedom and quadrature. For scalar finite elements, it will induce a diagonal mass matrix. For vectorial finite elements (such as edge elements), the mass matrix will be block-diagonal with small blocks.
Example :
HexahedronLobatto hex; hex.ConstructFiniteElement(3); // should return true here bool lumping = hex.LumpedMassMatrix();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
MassLumpingOrthogonalElement
Syntax
| bool MassLumpingOrthogonalElement() const |
This method returns true if the finite element class achieves mass lumping when the elements are orthogonal (i.e. the jacobian matrix DFi is uniform and diagonal). For hexahedra, orthogonal elements are rectangular parallelepipeds. If the mesh contains only orthogonal elements, the mass matrix will be diagonal.
Example :
HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // should return true here // mass lumping for orthogonal elements, but not for any element bool lumping = hex.MassLumpingOrthogonalElement();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
DiagonalMassMatrix
Syntax
| bool DiagonalMassMatrix() const |
This method returns true if the finite element class achieves mass lumping and that the mass matrix is diagonal. Usually it will be the case only for scalar elements. For vectorial elements, the mass lumping will induce a block-diagonal mass matrix.
Example :
HexahedronHcurlLobatto hex; hex.ConstructFiniteElement(3); // should return false here (mass lumping, but block-diagonal mass matrix) bool diag_mass = hex.DiagonalMassMatrix();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
DiscontinuousElement
Syntax
| bool DiscontinuousElement() const |
This method returns true if the finite element class can only be used with a discontinuous Galerkin formulation. For exemple, the class QuadrangleDgGauss constructs basis functions that are interpolatory polynomials based on Gauss-Legendre points, that do not include extremities. As a result, these basis functions cannot be used to construct a continuous approximation of a field.
Example :
HexahedronDgGauss hex; hex.ConstructFiniteElement(3); // should return true here bool dg_only = hex.DiscontinuousElement();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
UsePiolaTransform
Syntax
| bool UsePiolaTransform() const |
This method returns true if the finite element class will use Piola transform. This transform is relevant only for vectorial elements. For edge elements, we have the relation
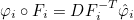
Thanks to this Piola transform, the basis functions can be used to approximate H(curl) space. If Piola transform is not used, we will have the relation
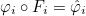
and the finite element can be used only with a discontinuous Galerkin formulation. By default, the Piola transform is used.
Example :
HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // should return true here bool piola = hex.UsePiolaTransform();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
SetPiolaTransform
Syntax
| void SetPiolaTransform(bool piola) const |
This method enables or disables the use of the Piola transform. This transform is explained in the method UsePiolaTransform. In regular use, this method does not need to be called.
Example :
HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // if you want to disable the use of Piola transform hex.SetPiolaTransform(false);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
Syntax
| bool OptimizedComputationMassMatrix() const |
This method returns true if the finite element class implements an optimized computation of the mass matrix. The naive algorithm has a complexity of O(r6) in 2-D and O(r9) in 3-D. Usually, it is the case of finite elements with tensorized basis functions. For these elements, the optimized algorithm will usually have a complexity in O(r5) in 2-D and O(r7) in 3-D.
Example :
HexahedronHierarchic hex; hex.ConstructFiniteElement(3); // should return true bool opt_mass = hex.OptimizedComputationMassMatrix();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
Syntax
| bool OptimizedComputationElementaryMatrix() const |
This method returns true if the finite element class implements an optimized computation of the elementary finite element matrices. The naive algorithm has a complexity of O(r6) in 2-D and O(r9) in 3-D. Usually, it is the case of finite elements with tensorized basis functions. For these elements, the optimized algorithm will usually have a complexity in O(r5) in 2-D and O(r7) in 3-D.
Example :
HexahedronHierarchic hex; hex.ConstructFiniteElement(3); // should return true bool opt_mass = hex.OptimizedComputationElementaryMatrix();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
SparseMassMatrix
Syntax
| bool SparseMassMatrix() const |
This method returns true if the elementary mass matrix is sparse. This is the case if there is a mass lumping (total or partial).
Example :
WedgeLobatto wed; // here partial mass lumping in z only wed.ConstructFiniteElement(3); // should return true bool sparse_mass = wed.SparseMassMatrix();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
LinearSparseMassMatrix
Syntax
| bool LinearSparseMassMatrix() const |
This method returns true if the elementary mass matrix is sparse for straight elements. This is the case if there is a total or partial orthogonality between basis functions.
Example :
WedgeHierarchic wed; wed.ConstructFiniteElement(3); // should return true bool sparse_mass = wed.LinearSparseMassMatrix();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
UseQuadraturePointsForSh
Syntax
| bool UseQuadraturePointsForSh() const |
This method returns true if it is more efficient to compute the matrix-vector with operator Sh with values on quadrature points. In that case, the methods ApplyShQuadrature, ApplyShQuadratureTranspose should be preferred over ApplySh, ApplyShTranspose.
Example :
HexahedronDgGauss hex; hex.ConstructFiniteElement(3); // is it better to compute Y = Sh X with values on quadrature points ? bool answer = hex.UseQuadraturePointsForSh();
Related topics:
ApplyShQuadrature, ApplyShQuadratureTranspose
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
UseQuadraturePointsForRh
Syntax
| bool UseQuadraturePointsForRh() const |
This method returns true if it is more efficient to compute the matrix-vector with operator Rh with values on quadrature points. In that case, the methods ApplyRhQuadrature, ApplyRhQuadratureTranspose should be preferred over ApplyRh, ApplyRhTranspose.
Example :
HexahedronDgGauss hex; hex.ConstructFiniteElement(3); // is it better to compute Y = Rh X with values on quadrature points ? bool answer = hex.UseQuadraturePointsForRh();
Related topics:
ApplyRhQuadrature, ApplyRhQuadratureTranspose
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
UseQuadratureFreeSh
Syntax
| bool UseQuadratureFreeSh() const |
This method returns true if the operator Sh is evaluated without quadrature points. This is possible only for affine faces (such as triangles or rectangles).
Example :
HexahedronDgGauss hex; hex.ConstructFiniteElement(3); // Sh without quadrature points ? bool answer = hex.UseQuadratureFreeRh();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetMaximalOrderRestriction
Syntax
| int GetMaximalOrderRestriction() const |
This method returns the maximal advised order rrmax to store the prolongation/restriction operator. If r is greater than rrmax, it is advised to not store this operator. The prolongation operator is the operator that prolongates a finite element solution to a higher order approximation, usually by interpolation:
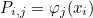
where φj are basis functions of the coarse order, and xi interpolation points of the fine order. The restriction operator is the transpose of the prolongation operator P.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); // we retrieve rmax int rmax = pyr.GetMaximalOrderRestriction(); if (pyr.GetOrder() <= rmax) cout << "It is better to store the restriction operator" << endl;
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetOrder
Syntax
| int GetOrder() const |
This method returns the order of approximation for the constructed element.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(3); // should return 3 int r = pyr.GetOrder();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetQuadratureOrder
Syntax
| int GetQuadratureOrder() const |
This method returns the order of integration for the constructed element.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3, 2, 4); // should return 4 int r = hex.GetQuadratureOrder();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetNbDof
Syntax
| int GetNbDof() const |
This method returns the number of degrees of freedom for the constructed element.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // should return 4^3 = 64 dofs int nb_dof = hex.GetNbDof();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetNbPointsQuadratureInside
Syntax
| int GetNbPointsQuadratureInside() const |
This method returns the number of integration points used for volume integrals. Volume integrals can be evaluated as
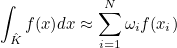
The method returns the integer N.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // should return 4^3 = 64 quadrature points for 3-D integrals int nb_quad = hex.GetNbPointsQuadratureInside();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetNbPointsQuadBoundaries, GetNbPointsUsedForSh
Syntax
| int GetNbPointsQuadBoundaries() const |
| int GetNbPointsUsedForSh() const |
This method returns the number of integration points used for surface integrals. Surface integrals can be evaluated as
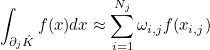
where j stands for the face number. The method returns the sum of integers Nj.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // should return 4^2 x 6 = 96 points for surface integrals int nb_quad_surf = hex.GetNbPointsQuadBoundaries();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetNbDofBoundaries
Syntax
| int GetNbDofBoundaries() const |
This method returns the number of degrees of freedom associated with the vertices and edges of the element (in 2-D), vertices, edges and faces of the element (in 3-D).
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // should return 4^3 - 2^3 = 56 dofs on the boundary of the element (8 interior dofs) int nb_dof_bord = hex.GetNbDofBoundaries();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetNbPointsDofInside
Syntax
| int GetNbPointsDofInside() const |
This method returns the number of points used to project a field on the degrees of freedom.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // we want to project a function to the finite element space (on the reference element) int nb_pts = hex.GetNbPointsDofInside(); // number of points where the function will be evaluated // evaluation of the function f = exp(-|| x ||) on dof points VectReal_wp feval(nb_pts); for (int i = 0; i < nb_pts; i++) feval(i) = exp(-Norm2(hex.PointsDofND(i))); // projection on basis functions VectReal_wp u; hex.ComputeProjectionDofRef(feval, u); // u = \sum u_i phi_i is an approximation of f
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetNbPointsDofSurface
Syntax
| int GetNbPointsDofSurface(int num_loc) const |
This method returns the number of points used to project a surface field on the degrees of freedom of the surface finite element (trace of the finite element on a face (edge in 2-D) of the element).
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // we want to project a surface function to the surface finite element space int num_loc = 2; // local number of the face int nb_pts = hex.GetNbPointsDofSurface(num_loc); // number of points where the function will be evaluated // evaluation of the function f = exp(-|| x ||) on dof points VectReal_wp feval(nb_pts); for (int i = 0; i < nb_pts; i++) feval(i) = exp(-Norm2(hex.PointsDofND(hex.GetPointDofNumber(num_loc, i)))); // projection on basis functions of surface finite element VectReal_wp u; hex.ComputeProjectionSurfaceDofRef(feval, u, num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetPointDofNumber
Syntax
| int GetPointDofNumber(int num_loc, int i) const |
This method returns the point dof number of the i-th surface dof.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // we want to project a surface function to the surface finite element space int num_loc = 2; // local number of the face int nb_pts = hex.GetNbPointsDofSurface(num_loc); // number of points where the function will be evaluated // evaluation of the function f = exp(-|| x ||) on dof points VectReal_wp feval(nb_pts); // here num = hex.GetPointDofNumber(num_loc, i) is the point dof number // PointsDofND(num) will be the i-th dof point located on the face num_loc for (int i = 0; i < nb_pts; i++) feval(i) = exp(-Norm2(hex.PointsDofND(hex.GetPointDofNumber(num_loc, i)))); // projection on basis functions of surface finite element VectReal_wp u; hex.ComputeProjectionSurfaceDofRef(feval, u, num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetQuadNumber
Syntax
| int GetQuadNumber(int num_loc, int i) const |
This method returns the quadrature point number of the i-th quadrature point of the face num_loc.
Example :
HexahedronGauss hex;
hex.ConstructFiniteElement(3);
// we want to compute a surface integral \int_{\partial_j \hat{K}} f(x) \hat{\varphi}_i(x) dx
int num_loc = 2;
int nb_quad = hex.GetNbQuadBoundary(num_loc);
// evaluation of the function f = exp(-|| x ||) on quadrature points
VectReal_wp feval(nb_quad);
// here num = hex.GetQuadNumber(num_loc, i) is the quadrature point number
// PointsND(num) will be the coordinates of this point
for (int i = 0; i < nb_quad; i++)
feval(i) = exp(-Norm2(hex.PointsND(hex.GetQuadNumber(num_loc, i))))
*hex.WeightsQuadratureBoundary(i, num_loc);
// computation of the surface integral
VectReal_wp u;
hex.ComputeIntegralSurfaceRef(feval, u, num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetQuadNumbersBoundary
Syntax
| const Vector<IVect>& GetQuadNumbersBoundary() const |
This method returns the quadrature point numbers of the faces (edges in 2-D) of an element.
Example :
HexahedronGauss hex;
hex.ConstructFiniteElement(3);
// we want to compute a surface integral \int_{\partial_j \hat{K}} f(x) \hat{\varphi}_i(x) dx
int num_loc = 2;
int nb_quad = hex.GetNbQuadBoundary(num_loc);
// evaluation of the function f = exp(-|| x ||) on quadrature points
VectReal_wp feval(nb_quad);
// quadrature point numbers for all the faces
const Vector<IVect>& num_quad = hex.GetQuadNumbersBoundary();
for (int i = 0; i < nb_quad; i++)
feval(i) = exp(-Norm2(hex.PointsND(num_quad(num_loc)(i))))
*hex.WeightsQuadratureBoundary(i, num_loc);
// computation of the surface integral
VectReal_wp u;
hex.ComputeIntegralSurfaceRef(feval, u, num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetOffsetSh
Syntax
| int GetOffsetSh(int num_loc) const |
This method returns the offset for quadrature point numbers for the face num_loc. Surface integrals can be evaluated as
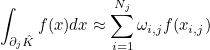
where j stands for the face number. The method returns the sum of integers Nj from j = 0 until j=num_loc-1.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // incremented number of quadrature points until face num_loc int num_loc = 2; int offset_quad = hex.GetOffsetSh(num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
SetQuadNumbersBoundary
Syntax
| void SetQuadNumbersBoundary(const Vector<IVect>& num) |
This method sets the quadrature point numbers (as returned by GetQuadNumber) of the faces (edges in 2-D) of the element. This method should not be used in a regular use, since these numbers are already constructed by ConstructFiniteElement.
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
SetDofNumbersBoundary
Syntax
| void SetDofNumbersBoundary(const Vector<IVect>& num) |
This method sets the dof point numbers of the faces (edges in 2-D) of the element. This method should not be used in a regular use, since these numbers are already constructed by ConstructFiniteElement.
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetTypeIntegrationEdge
Syntax
| int GetTypeIntegrationEdge() const |
This method returns the type of integration used for the unit interval [0, 1], as expected in the method ConstructQuadrature of the class Globatto. For 2-D elements, this is the integration rule used for the evaluation of boundary integrals.
Example :
QuadrangleLobatto quad; quad.ConstructFiniteElement(3); // type of integration for edges int type_quad = quad.GetTypeIntegrationEdge(); if (type_quad == Globatto<Real_wp>::QUADRATURE_LOBATTO) cout << "Using Gauss-Lobatto points" << endl;
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetTypeIntegrationTriangle
Syntax
| int GetTypeIntegrationTriangle() const |
This method returns the type of integration used for the unit triangle, as expected in the method ConstructQuadrature of the class TriangleQuadrature. For 3-D elements, this is the integration rule used for the evaluation of boundary integrals. This method is not relevant for 2-D elements.
Example :
TetrahedronClassical tet; tet.ConstructFiniteElement(3); // type of integration for triangular faces int type_tri = tet.GetTypeIntegrationTriangle(); if (type_quad == TriangleQuadrature::QUADRATURE_GAUSS) cout << "Using Dunavant's points" << endl;
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
GetTypeIntegrationQuadrangle
Syntax
| int GetTypeIntegrationQuadrangle() const |
This method returns the type of integration used for the unit square, as expected in the method ConstructQuadrature of the class QuadrangleQuadrature. For 3-D elements, this is the integration rule used for the evaluation of boundary integrals. This method is not relevant for 2-D elements.
Example :
WedgeClassical wed; wed.ConstructFiniteElement(3); // type of integration for quadrangular faces int type_quad = wed.GetTypeIntegrationQuadrangle(); if (type_quad == Globatto<Real_wp>::QUADRATURE_GAUSS) cout << "Using Gauss points" << endl;
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
IsTangentialDof
Syntax
| bool IsTangentialDof(int j, int num_loc) const |
This method returns true if the j-th dof belongs to the face (edge in 2-D) num_loc. A dof associated with an edge of the face will also be considered a dof of the face in this method. We say tangential dofs, because for edge elements the dofs on the face are dofs that will contribute to the tangential trace of a field. Basis functions associated with other dofs may will have a null tangential trace on the face. For facet elements, dofs of the face will contribute to the normal trace of the field.
Example :
HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // is dof 11 a dof of the face num_loc ? int num_loc = 2; bool dof_on_face = hex.IsTangentialDof(11, num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
WeightsND
Syntax
| Real_wp WeightsND(int i) const |
| const VectReal_wp& WeightsND() const |
This method returns a single integration weight or all the weights. These weights can be used for volume integrals.
Example :
HexahedronGauss hex;
hex.ConstructFiniteElement(3);
// number of quadrature points for a volume integral
int nb_quad = hex.GetNbPointsQuadratureInside();
// integration against basis functions (you need to multiply with the weights)
// contrib(i) = \int_{\hat{K}} exp(-r^2)* varphi_i
for (int i = 0; i < nb_quad; i++)
feval(i) = hex.WeightsND(i)*exp(-DotProd(hex.PointsND(i), hex.PointsND(i)));
Vector<double> contrib;
hex.ComputeIntegralRef(feval, contrib);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
WeightsDofND
Syntax
| Real_wp WeightsDofND(int i) const |
| const VectReal_wp& WeightsDofND() const |
This method returns a single integration weight or all the weights. These weights are the weights associated with dof points. They are relevant only if dof points (used by ComputeProjectionDofRef) can be used as integration points.
Example :
HexahedronGauss hex;
hex.ConstructFiniteElement(3);
// number of dof points
int nb_quad = hex.GetNbPointsDofInside();
// integration of a function res = \int_{\hat{K}} f(x) dx where f = exp(-||x||^2)
// we use dof points instead of quadrature points
Real_wp res = 0;
for (int i = 0; i < nb_quad; i++)
res += hex.WeightsDofND(i)*exp(-DotProd(hex.PointsDofND(i), hex.PointsDofND(i)));
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
WeightsDofND
Syntax
| const VectReal_wp& GetFluxWeight(int num_loc) const |
This method returns the half-weights to use for a boundary integral over the face num_loc. Half-weights are returned instead of weights because numerical fluxes for discontinuous Galerkin formulation usually involves terms 1/2 (u1 + u2) or 1/2 (u1 - u2). Hence the factor 1/2 is already integrated in the returned array.
Example :
HexahedronGauss hex;
hex.ConstructFiniteElement(3);
// weights divided by two
int num_loc = 2;
const VectReal_wp& poids = hex.GetFluxWeight(num_loc);
// integration of a function res = 1/2 \int_{\partial_j \hat{K}} f(x) dx where f = exp(-||x||^2)
Real_wp res = 0;
for (int i = 0; i < poids.GetM(); i++)
{
int num = hex.GetQuadNumber(num_loc, i);
res += poids(i)*exp(-DotProd(hex.PointsND(num), hex.PointsND(num)));
}
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBaseInline.cxx
ComputeGaussIntegralSurfaceRef
Syntax
| void ComputeGaussIntegralSurfaceRef(const Vector& feval, Vector& res, int num_loc) const |
This method computes a boundary integral with basis functions. The integration is performed with accurate integration (like Gauss points instead of Gauss-Lobatto points). The resulting vector res is equal to
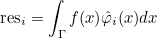
where Γ is a face (edge in 2-D) of the reference element, f a given function and φi basis functions of the finite element class. Since weights are included in input vector feval, the resulting vector is equal to
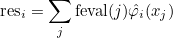
where xj are Gauss quadrature points of the local face num_loc. The vectors feval and res can be either real-valued or complex-valued.
Parameters
- feval (in)
- Evaluation of f on Gauss points (multiplied by integration weights)
- res (out)
- resulting vector
- num_loc (in)
- local number of the face Γ
Example :
QuadrangleLobatto quad;
int order = 4;
quad.ConstructFiniteElement(order);
// Evaluating Gauss formula
Globatto<Real_wp> gauss;
gauss.ConstructQuadrature(order);
// evaluating f on quadrature points of the edge
int num_loc = 1; R2 point;
for (int i = 0; i <= order; i++)
{
// position of the integration point on the edge
quad.GetLocalCoordOnBoundary(num_loc, gauss.Points(i), point);
feval(i) = exp(-Dot(point, point)) * gauss.Weights(i);
}
// then integration against basis functions
VectReal_wp res;
quad.ComputeGaussIntegralSurfaceRef(feval, res, num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyRhQuadrature
Syntax
| void ApplyRhQuadrature(const Vector& feval, Vector& res) const |
This method computes an integral with gradient of basis functions associated with quadrature points. The resulting vector res is equal to
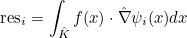
where f is a given function and ψi are basis functions associated with quadrature points. The gradient is replaced by a curl for edge elements, and a divergence for facet elements. This method is relevant only if the quadrature points can be associated with basis functions, therefore this method is available only if UseQuadraturePointsForRh returns true. Since weights are included in input vector feval, the resulting vector is equal to
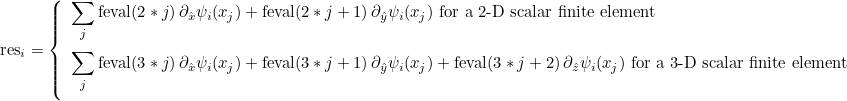
where xj are quadrature points of the reference element. For edge and facet elements, the divergence and curl are involved:
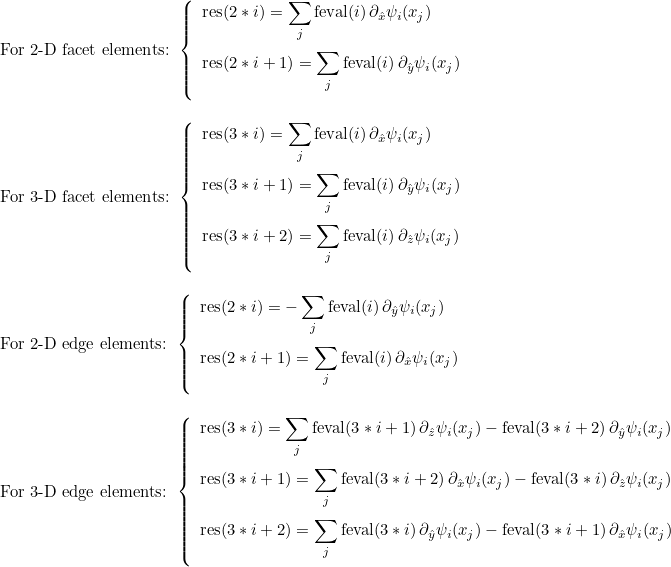
If the method UseQuadraturePointsForRh returns true, it means that the method ApplyRh consists of a call to ApplyRhQuadrature followed by a call to ApplyCh. So it can be interesting to call ApplyRhQuadrature and regroup with mass terms before calling AppyCh.
Parameters
- feval (in)
- Evaluation of f on quadrature points (multiplied by integration weights)
- res (inout)
- resulting vector (allocated on input)
Example :
HexahedronHcurlFirstFamily hex;
int order = 4;
hex.ConstructFiniteElement(order);
// function to evaluate f = (-y^2, z^2, x*y)
VectReal_wp feval(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
Real_wp x = hex.PointsND(i)(0), y = hex.PointsND(i)(1), z = hex.PointsND(i)(2);
Real_wp poids = hex.WeightsND(i);
feval(3*i) = -y*y*poids; feval(3*i+1) = z*z*poids; feval(3*i+2) = x*y*poids;
}
// integration against curl of basis functions (based on quadrature points)
VectReal_wp res(3*hex.GetNbPointsQuadratureInside());
hex.ApplyRhQuadrature(feval, res);
// then if you want to have the integral against true basis functions => ApplyCh
VectReal_wp res_final(hex.GetNbDof());
hex.ApplyCh(res, res_final);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyRhQuadratureTranspose
Syntax
| void ApplyRhQuadratureTranspose(const Vector& uquad, Vector& res) const |
This method is the transpose operation of ApplyRhQuadrature. It computes the gradient of a field on quadrature points
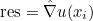
where u is a given field and xi quadrature points. The gradient is replaced by a curl for edge elements, and a divergence for facet elements. This method is relevant only if the quadrature points can be associated with basis functions, therefore this method is available only if UseQuadraturePointsForRh returns true. The values of the field u are known only on quadrature points (stored in the input vector uquad). The resulting vector is equal to

where ψi are basis functions associated with quadrature points of the reference element. If the method UseQuadraturePointsForRh returns true, it means that the method ApplyRhTranspose consists of a call to ApplyChTranspose followed by a call to ApplyRhQuadratureTranspose. So it can be interesting to call ApplyRhQuadratureTranspose if you have already computed the values on quadrature points with AppyChTranspose.
Parameters
- uquad (in)
- values of u on quadrature points
- res (inout)
- resulting vector (allocated on input)
Example :
HexahedronHcurlFirstFamily hex; int order = 4; hex.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(hex.GetNbDof()); u.FillRand(); // we compute the values of u on quadrature points VectReal_wp uquad(3*hex.GetNbPointsQuadratureInside()); hex.ApplyChTranspose(u, uquad); // then we compute the curl VectReal_wp curl_u(3*hex.GetNbPointsQuadratureInside()); hex.ApplyRhQuadratureTranspose(uquad, curl_u);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyRhBoundaryTranspose
Syntax
| void ApplyRhBoundaryTranspose(const Vector& u, Vector& res) const |
This method computes the gradient of a field on quadrature points located on the boundary. These quadrature points are not quadrature points associated with the face, but indeed volume quadrature points (as returned by PointsND that lie on the boundary of the element. In ApplyRh, the gradient is computed for all quadrature points. The method is implemented only for QuadrangleLobatto and HexahedronLobatto.
Parameters
- u (in)
- field u
- res (inout)
- resulting vector (allocated on input)
Example :
HexahedronLobatto hex; int order = 4; hex.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(hex.GetNbDof()); u.FillRand(); // we want to know values of grad(u) only for quadrature points on the boundary of the unit cube : VectReal_wp grad_u(3*hex.GetNbDofBoundaries()); hex.ApplyRhBoundaryTranspose(u, grad_u);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyRhBoundary
Syntax
| void ApplyRhBoundary(const Vector& feval, Vector& res) const |
This method is the transpose operator of ApplyRhBoundaryTranspose. It consists of computing the integral of a function f against the gradient of basis functions, assuming that the function to integrate is non-nul only for quadrature points located on the boundary. This method is implemented only for QuadrangleLobatto and HexahedronLobatto.
Parameters
- feval (in)
- evaluation of f on quadrature points of the boundary (multiplied by weights)
- res (inout)
- resulting vector (allocated on input)
Example :
HexahedronLobatto hex; int order = 4; hex.ConstructFiniteElement(order); // we start from a function to integrate (null for quadrature points strictly inside the reference element VectReal_wp feval(3*hex.GetNbDofBoundaries()); feval.RillRand(); // then integration against gradient of basis functions VectReal_wp res(hex.GetNbDof()); hex.ApplyRhBoundary(feval, res);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyShTranspose
Syntax
| void ApplyShTranspose(int num_loc, const Vector& u, Vector& res, int order) const |
This method computes the values of a field on quadrature points associated with the face num_loc:
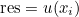
where xi are quadrature points of the face num_loc. The resulting vector is equal to
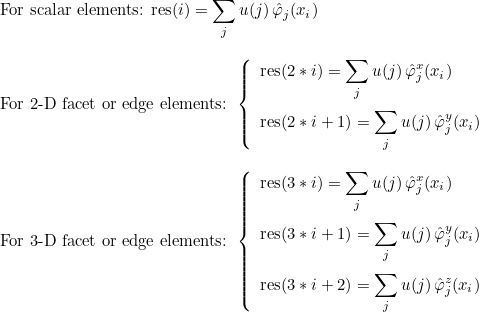
where φj are basis functions. If the optional parameter order is provided, there is an additional projection to compute the values on quadrature points of the face for the required order.
Parameters
- num_loc (in)
- local number of the face
- u (in)
- field u
- res (inout)
- resulting vector (allocated on input)
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(pyr.GetNbDof()); u.FillRand(); // we want to know values of u for quadrature points of a face int num_loc = 3; VectReal_wp uface(pyr.GetNbQuadBoundary(num_loc)); pyr.ApplyShTranspose(num_loc, u, uface);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplySh
Syntax
| void ApplySh(Real_wp alpha, int num_loc, const Vector& feval, Vector& res, int order) const |
This method is the transpose operation of ApplyShTranspose. It adds to the vector res the boundary integral against basis functions:
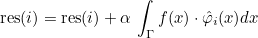
where f is a given function and φi are basis functions. Since weights are included in input vector feval, the resulting vector is equal to
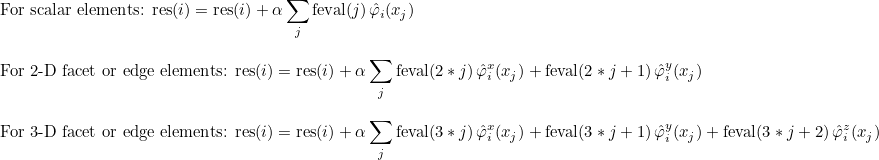
If the optional parameter order is provided, there is an additional projection to interpolate feval from the quadrature points of the face for the given order.
Parameters
- alpha (in)
- coefficient
- num_loc (in)
- local number of the face
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < feval.GetM(); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
feval(i) = exp(-Dot(pt3D, pt3D));
feval(i) *= pyr.WeightsQuadratureBoundary(i, num_loc);
}
VectReal_wp res(pyr.GetNbDof());
res.Zero();
// we want to add the integral against basis functions
// the integral is made over a face
pyr.ApplySh(Real_wp(1), num_loc, feval, res);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyShQuadratureTranspose
Syntax
| void ApplyShQuadratureTranspose(int num_loc, const Vector& u, Vector& res, int order) const |
This method computes the values of a field on quadrature points associated with the face num_loc:
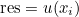
where xi are quadrature points of the face num_loc. The resulting vector is equal to
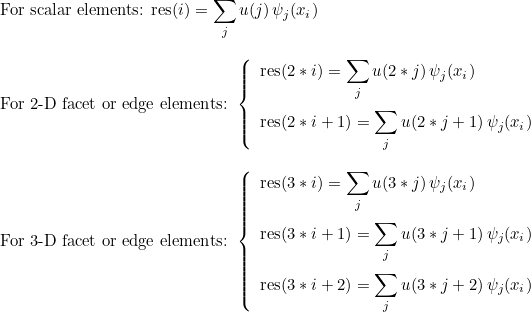
where ψj are basis functions associated with the quadrature points of the reference element. If the optional parameter order is provided, there is an additional projection to compute the values on quadrature points of the face for the required order. If the method UseQuadraturePointsForSh returns true, this method can be used and is of interest if you have already computed the values of u on the quadrature points.
Parameters
- num_loc (in)
- local number of the face
- u (in)
- values of u on quadrature points of the reference element
- res (inout)
- resulting vector (allocated on input)
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(pyr.GetNbDof()); u.FillRand(); // computation on quadrature points VectReal_wp uquad(pyr.GetNbPointsQuadratureInside()); pyr.ApplyChTranspose(u, uquad); // we want to know values of u for quadrature points of a face int num_loc = 3; VectReal_wp uface(pyr.GetNbQuadBoundary(num_loc)); pyr.ApplyShQuadratureTranspose(num_loc, uquad, uface);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyShQuadrature
Syntax
| void ApplyShQuadrature(Real_wp alpha, int num_loc, const Vector& feval, Vector& res, int order) const |
This method is the transpose operation of ApplyShQuadratureTranspose. It adds to the vector res the boundary integral against basis functions associated with the quadrature points:
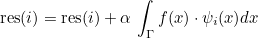
where f is a given function and ψi are basis functions associated with quadrature points. Since weights are included in input vector feval, the resulting vector is equal to
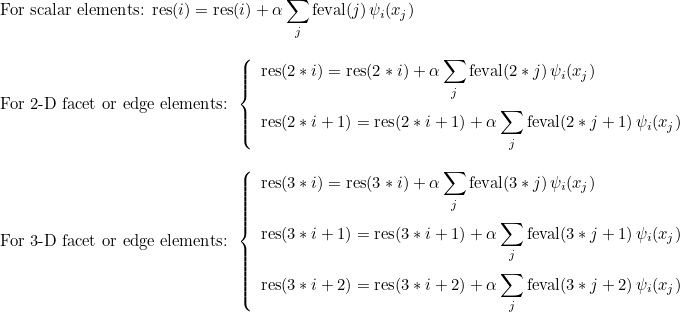
If the optional parameter order is provided, there is an additional projection to interpolate feval from the quadrature points of the face for the given order. If the method UseQuadraturePointsForSh returns true, this method should be used instead of ApplySh.
Parameters
- alpha (in)
- coefficient
- num_loc (in)
- local number of the face
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < feval.GetM(); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
feval(i) = exp(-Dot(pt3D, pt3D));
feval(i) *= pyr.WeightsQuadratureBoundary(i, num_loc);
}
VectReal_wp res(pyr.GetNbPointsQuadratureInside());
res.Zero();
// we want to add the integral against basis functions of quadrature points
// the integral is made over a face
pyr.ApplyShQuadrature(Real_wp(1), num_loc, feval, res);
// then if you want to obtain contributions for the true basis functions => ApplyCh
VectReal_wp contrib(pyr.GetNbDof());
pyr.ApplyCh(res, contrib);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyNablaShTranspose
Syntax
| void ApplyNablaShTranspose(int num_loc, const Vector& u, Vector& res, int order) const |
This method computes the gradient of a field on quadrature points associated with the face num_loc:
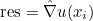
where xi are quadrature points of the face num_loc. The gradient is replaced by the curl for edge elements and by the divergence for facet elements. The resulting vector is equal to
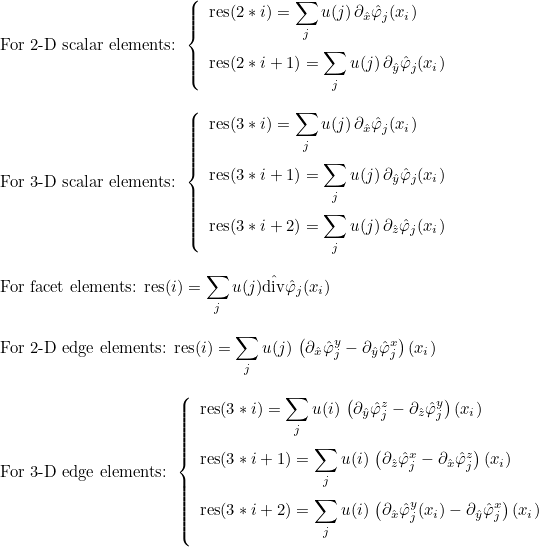
where φj are basis functions. If the optional parameter order is provided, there is an additional projection to compute the values on quadrature points of the face for the required order.
Parameters
- num_loc (in)
- local number of the face
- u (in)
- field u
- res (inout)
- resulting vector (allocated on input)
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(pyr.GetNbDof()); u.FillRand(); // we want to know gradient of u for quadrature points of a face int num_loc = 3; VectReal_wp uface(3*pyr.GetNbQuadBoundary(num_loc)); pyr.ApplyNablaShTranspose(num_loc, u, uface);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyNablaSh
Syntax
| void ApplyNablaSh(Real_wp alpha, int num_loc, const Vector& feval, Vector& res, int order) const |
This method is the transpose operation of ApplyNablaShTranspose. It adds to the vector res the boundary integral against gradient of basis functions:
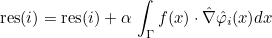
where f is a given function and φi are basis functions. The gradient is replaced by the curl for edge elements and by the divergence for facet elements. Since weights are included in input vector feval, the resulting vector is equal to
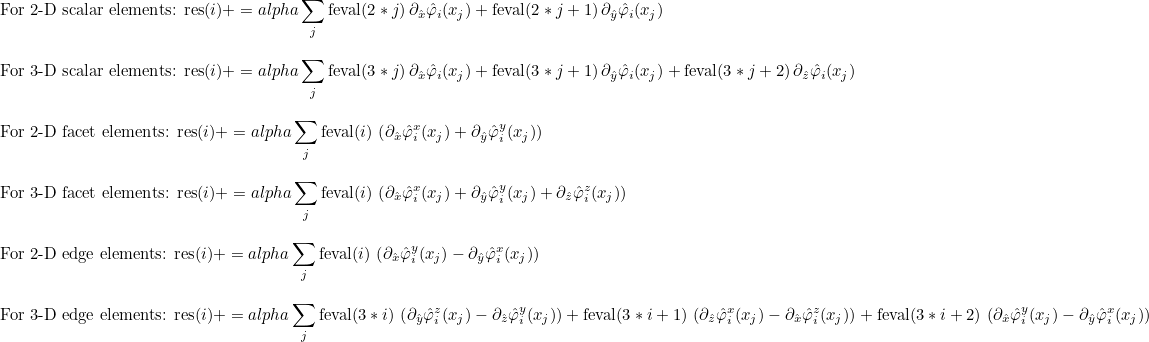
If the optional parameter order is provided, there is an additional projection to interpolate feval from the quadrature points of the face for the given order.
Parameters
- alpha (in)
- coefficient
- num_loc (in)
- local number of the face
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(3*pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < pyr.GetNbQuadBoundary(num_loc); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
feval(3*i) = exp(-Dot(pt3D, pt3D));
feval(3*i) *= pyr.WeightsQuadratureBoundary(i, num_loc);
feval(3*i+1) = exp(-Dot(pt3D, pt3D)*0.4);
feval(3*i+1) *= pyr.WeightsQuadratureBoundary(i, num_loc);
feval(3*i+2) = exp(-Dot(pt3D, pt3D)*0.8);
feval(3*i+2) *= pyr.WeightsQuadratureBoundary(i, num_loc);
}
VectReal_wp res(pyr.GetNbDof());
res.Zero();
// we want to add the integral against gradient of basis functions
// the integral is made over a face
pyr.ApplyNablaSh(Real_wp(1), num_loc, feval, res);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyNablaShQuadratureTranspose
Syntax
| void ApplyNablaShQuadratureTranspose(int num_loc, const Vector& uquad, Vector& res, int order) const |
This method computes the gradient of a field on quadrature points associated with the face num_loc:
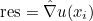
where xi are quadrature points of the face num_loc. The gradient is replaced by the curl for edge elements and by the divergence for facet elements. The resulting vector is equal to

where ψj are basis functions associated with the quadrature points of the reference element. If the optional parameter order is provided, there is an additional projection to compute the values on quadrature points of the face for the required order. If the method UseQuadraturePointsForSh returns true, this method can be used and is of interest if you have already computed the values of u on the quadrature points.
Parameters
- num_loc (in)
- local number of the face
- uquad (in)
- values of u on quadrature points of the reference element
- res (inout)
- resulting vector (allocated on input)
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(pyr.GetNbDof()); u.FillRand(); // computation on quadrature points VectReal_wp uquad(pyr.GetNbPointsQuadratureInside()); pyr.ApplyChTranspose(u, uquad); // we want to know gradient of u for quadrature points of a face int num_loc = 3; VectReal_wp grad_uface(3*pyr.GetNbQuadBoundary(num_loc)); pyr.ApplyNablaShQuadratureTranspose(num_loc, uquad, grad_uface);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyNablaShQuadrature
Syntax
| void ApplyNablaShQuadrature(Real_wp alpha, int num_loc, const Vector& feval, Vector& res, int order) const |
This method is the transpose operation of ApplyNablaShQuadratureTranspose. It adds to the vector res the boundary integral against basis functions associated with the quadrature points:
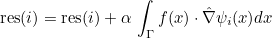
where f is a given function and ψi are basis functions associated with quadrature points. The gradient is replaced by a curl for edge elements, and a divergence for facet elements. This method is relevant only if the quadrature points can be associated with basis functions, therefore this method is available only if UseQuadraturePointsForSh returns true. Since weights are included in input vector feval, the resulting vector is equal to

If the optional parameter order is provided, there is an additional projection to interpolate feval from the quadrature points of the face for the given order. If the method UseQuadraturePointsForSh returns true, this method should be used instead of ApplyNablaSh.
Parameters
- alpha (in)
- coefficient
- num_loc (in)
- local number of the face
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- order (optional)
- order for quadrature points of the face
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(3*pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < feval.GetM(); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
feval(3*i) = exp(-Dot(pt3D, pt3D));
feval(3*i) *= pyr.WeightsQuadratureBoundary(i, num_loc);
feval(3*i+1) = exp(-Dot(pt3D, pt3D)*0.4);
feval(3*i+1) *= pyr.WeightsQuadratureBoundary(i, num_loc);
feval(3*i+2) = exp(-Dot(pt3D, pt3D)*0.8);
feval(3*i+2) *= pyr.WeightsQuadratureBoundary(i, num_loc);
}
VectReal_wp res(pyr.GetNbPointsQuadratureInside());
res.Zero();
// we want to add the integral against gradient of basis functions of quadrature points
// the integral is made over a face
pyr.ApplyNablaShQuadrature(Real_wp(1), num_loc, feval, res);
// then if you want to obtain contributions for the true basis functions => ApplyCh
VectReal_wp contrib(pyr.GetNbDof());
pyr.ApplyCh(res, contrib);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
SolveMassMatrix
Syntax
| void SolveMassMatrix(Vector& x) const |
This method replaces the vector x by the solution y of the linear system
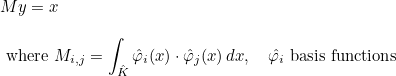
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// starting from an initial vector x
VectReal_wp x(pyr.GetNbDof()); x.FillRand();
// we want to replace x by M^{-1} x where M is the mass matrix on the reference element
pyr.SolveMassMatrix(x);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
SolveCholesky
Syntax
| void SolveCholesky(const SeldonTranspose& trans, Vector& x) const |
This method replaces the vector x by L-1x or L-T x where L is the Cholesky factor of the mass matrix M (defined in the method SolveMassMatrix). Since M is symmetric positive definite, it admits the following Cholesky decomposition:
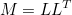
where L is a triangular matrix.
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// starting from an initial vector x
VectReal_wp x(pyr.GetNbDof()); x.FillRand();
// we want to replace x by L^{-1} x
pyr.SolveCholesky(SeldonNoTrans, x);
// then L^{-T} x
pyr.SolveCholesky(SeldonTrans, x);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
MltMassMatrix
Syntax
| void MltMassMatrix(Vector& x) const |
This method replaces the vector x by M x where M is the mass matrix (defined in the method SolveMassMatrix).
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // starting from an initial vector x VectReal_wp x(pyr.GetNbDof()); x.FillRand(); // we want to replace x by M x pyr.MltMassMatrix(x);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ComputeMassMatrix
Syntax
| void ComputeMassMatrix(Matrix& M, VectReal_wp& coef) const |
This method computes the mass matrix (on the real element) from the polynomial coefficients of the jacobian (as computed by ComputeCoefJacobian). It can be called only if the method LinearSparseMassMatrix returns true and for a non-curved element. It is the case for instance for classes PyramidDgOrtho or WedgeDgOrtho.
Example :
PyramidDgOrtho pyr; int order = 4; pyr.ConstructFiniteElement(order); // we compute the coefficients of jacobian for the desired element Mesh<Dimension3> mesh; VectR3 s; int num_elem = 42; mesh.GetVerticesElement(num_elem, s); VectReal_wp coef; pyr.ComputeCoefJacobian(s, coef); // we want to compute the mass matrix for this element Matrix<Real_wp, Symmetric, RowSymPacked> M; pyr.ComputeMassMatrix(M, coef); // then you can convert it to a sparse matrix if you want Matrix<Real_wp, Symmetric, ArrayRowSymSparse> Ms; ConvertToSparse(M, Ms, 1e-12);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
IntegrateMassMatrix
Syntax
| void IntegrateMassMatrix(Matrix& M, VectReal_wp& coef) const |
This method computes the mass matrix (on the real element) from the values of the weighted jacobian (jacobian multiplied by the integration weight) on quadrature points. It can be called only if the method OptimizedComputationMassMatrix returns true.
Example :
WedgeDgClassical wed; int order = 4; wed.ConstructFiniteElement(order); // we compute the values of weighted jacobian for the desired element Mesh<Dimension3> mesh; VectR3 s; int num_elem = 42; mesh.GetVerticesElement(num_elem, s); SetPoints<Dimension3> PointsElem; SetMatrices<Dimension3> MatricesElem; wed.FjElemNodal(s, PointsElem, mesh, num_elem); wed.DFjElemQuadrature(s, PointsElem, MatricesElem, mesh, num_elem); int Nquad = wed.GetNbPointsQuadratureInside(); VectReal_wp val_jacob(Nquad); for (int i = 0; i < Nquad; i++) val_jacob(i) = Det(MatricesElement.GetPointQuadrature(i))*wed.WeightsND(i); // we want to compute the mass matrix for this element Matrix<Real_wp, Symmetric, RowSymPacked> M; pyr.IntegrateMassMatrix(M, val_jacob); // then you can convert it to a sparse matrix if you want Matrix<Real_wp, Symmetric, ArrayRowSymSparse> Ms; ConvertToSparse(M, Ms, 1e-12);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
PickNearDofs
Syntax
| void PickNearDofs(int num_dof, VectBool& DofUsed, IVect& ListeDof, int nb_dof) const |
This method fills the array ListeDof with dof numbers that are "close" to the degree of freedom num_dof. It is meaningful for nodal finite elements for which a degree of freedom is associated with a point.
Parameters
- num_dof (in)
- dof number
- DofUsed (in)
- If DofUsed(i) is false, the dof i can be used to fill the array ListeDof
- ListeDof (out)
- list of dofs close to the degree of freedom num_dof
- nb_dof (in)
- number of degrees of freedom to pick close to the dof num_dof
Example :
TetrahedronClassical tet; int order = 4; tet.ConstructFiniteElement(order); int num_dof = 11; VectBool DofUsed(tet.GetNbDof()); DofUsed.Fill(false); // retrieving 3 dofs close to the dof 11 IVect close_dof; int nb_dof = 3; tet.PickNearDofs(num_dof, DofUsed, close_dof, nb_dof); // we update the array DofUsed for (int i = 0; i < close_dof.GetM(); i++) DofUsed(close_dof(i)) = true; // retrieving 5 dofs close to the dof 15 // but we do not select dofs already selected previously (thanks to array DofUsed) tet.PickNearDofs(15, DofUsed, close_dof, 5);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ConstructNumberMap
Syntax
| void ConstructNumberMap(NumberMap& number_map, int dg_formulation) const |
This method fills the object number_map with the number of dofs per vertex, edge, triangle, etc. In the second argument, we put the type of formulation (continuous, discontinuous or hdg) that will be used.
Example :
TetrahedronClassical tet; int order = 4; tet.ConstructFiniteElement(order); Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); // choose between CONTINUOUS, DISCONTINUOUS or HDG mesh_num.ConstructNumberMap(mesh_num.number_map, ElementReference_Base::CONTINUOUS); // then you can number the mesh mesh_num.NumberMesh();
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyChTranspose
Syntax
| void ApplyChTranspose(const Vector& u, Vector& u_quad) const |
This method is the transpose operation of ApplyCh. It computes the values of a field on quadrature points

where u is a given field and xi quadrature points. The resulting vector is equal to
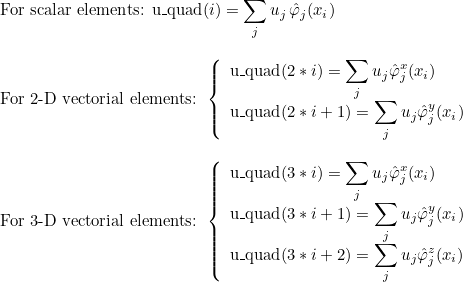
where
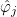 are basis functions of the reference element.
are basis functions of the reference element.
Parameters
- u (in)
- components of the field on degrees of freedom
- u_quad (inout)
- resulting vector (allocated on input)
Example :
HexahedronHcurlFirstFamily hex; int order = 4; hex.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(hex.GetNbDof()); u.FillRand(); // we compute the values of u on quadrature points VectReal_wp uquad(3*hex.GetNbPointsQuadratureInside()); hex.ApplyChTranspose(u, uquad);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ApplyCh
Syntax
| void ApplyCh(const Vector& feval, Vector& res) const |
This method is the transpose operation of ApplyChTranspose. It computes the integral against basis functions
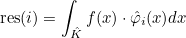
where f is a given function and φi are basis functions. The resulting vector is equal to
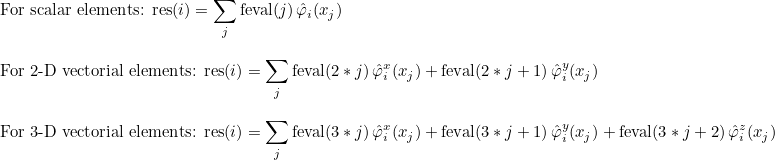
Parameters
- feval (in)
- Evaluation of f on quadrature points (multiplied by weights)
- res (inout)
- resulting vector (allocated on input)
Example :
HexahedronHcurlFirstFamily hex;
int order = 4;
hex.ConstructFiniteElement(order);
// function to evaluate f = (-y^2, z^2, x*y)
VectReal_wp feval(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
Real_wp x = hex.PointsND(i)(0), y = hex.PointsND(i)(1), z = hex.PointsND(i)(2);
Real_wp poids = hex.WeightsND(i);
feval(3*i) = -y*y*poids; feval(3*i+1) = z*z*poids; feval(3*i+2) = x*y*poids;
}
// integration against basis functions
VectReal_wp res(hex.GetNbDof());
hex.ApplyCh(feval, res);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ComputeProjectionDofRef
Syntax
| void ComputeProjectionDofRef(const Vector& feval, Vector& contrib) const |
This method projects a given function f in the finite element space. For nodal finite element, the projection will be trivial (contrib = feval). The projection is given as
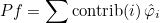
where φi are basis functions. f and Pf will be close for dof points (they coincide for some finite elements).
Parameters
- feval (in)
- Evaluation of f on dof points
- contrib (inout)
- resulting vector (allocated on input)
Example :
HexahedronHcurlFirstFamily hex;
int order = 4;
hex.ConstructFiniteElement(order);
// function to evaluate f = (-y^2, z^2, x*y) on dof points
VectReal_wp feval(3*hex.GetNbPointsDof());
for (int i = 0; i < hex.GetNbPointsDof(); i++)
{
Real_wp x = hex.PointsDofND(i)(0), y = hex.PointsDofND(i)(1), z = hex.PointsDofND(i)(2);
feval(3*i) = -y*y; feval(3*i+1) = z*z; feval(3*i+2) = x*y;
}
// projection on basis functions
VectReal_wp contrib(hex.GetNbDof());
hex.ComputeProjectionDofRef(feval, contrib);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ComputeProjectionSurfaceDofRef
Syntax
| void ComputeProjectionSurfaceDofRef(const Vector& feval, Vector& contrib, int num_loc) const |
This method projects a given function f on the boundary finite element space.
Parameters
- feval (in)
- Evaluation of f on dof points of the selected boundary
- contrib (inout)
- resulting vector (allocated on input)
- num_loc (in)
- boundary number
Example :
HexahedronHcurlFirstFamily hex;
int order = 4;
hex.ConstructFiniteElement(order);
int num_loc = 2;
// function to evaluate f = (-y^2, z^2, x*y) on dof points of the boundary
const VectR2& pts = hex.PointsDofBoundary(num_loc);
VectReal_wp feval(3*pts.GetM());
for (int i = 0; i < pts.GetM(); i++)
{
R3 point;
hex.GetLocalCoordOnBoundary(num_loc, pts(i), point);
Real_wp x = point(0), y = point(1), z = point(2);
feval(3*i) = -y*y; feval(3*i+1) = z*z; feval(3*i+2) = x*y;
}
// projection on basis functions of the boundary
VectReal_wp contrib(hex.GetNbDofBoundary(num_loc));
hex.ComputeProjectionSurfaceDofRef(feval, contrib);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ComputeIntegralRef
Syntax
| void ComputeIntegralRef(const Vector& feval, Vector& res) const |
This method is actually equivalent to the method ApplyCh. It computes the integral against basis functions
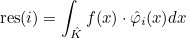
where f is a given function and φi are basis functions. The resulting vector is equal to
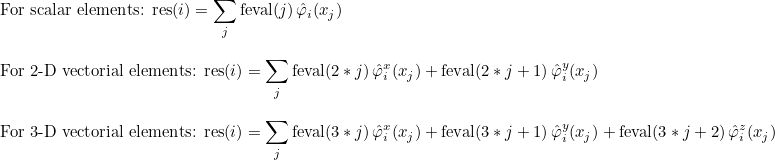
Parameters
- feval (in)
- Evaluation of f on quadrature points (multiplied by weights)
- res (inout)
- resulting vector (allocated on input)
Example :
HexahedronHcurlFirstFamily hex;
int order = 4;
hex.ConstructFiniteElement(order);
// function to evaluate f = (-y^2, z^2, x*y)
VectReal_wp feval(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
Real_wp x = hex.PointsND(i)(0), y = hex.PointsND(i)(1), z = hex.PointsND(i)(2);
Real_wp poids = hex.WeightsND(i);
feval(3*i) = -y*y*poids; feval(3*i+1) = z*z*poids; feval(3*i+2) = x*y*poids;
}
// integration against basis functions
VectReal_wp res(hex.GetNbDof());
hex.ComputeIntegralRef(feval, res);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
ComputeIntegralSurfaceRef
Syntax
| void ComputeIntegralSurfaceRef(const Vector& feval, Vector& res, int num_loc) const |
This method is similar to the method ApplySh. It computes the boundary integral against basis functions:
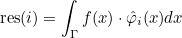
where f is a given function and φi are basis functions. Since weights are included in input vector feval, the resulting vector is equal to
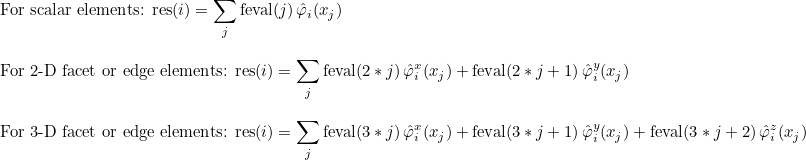
Parameters
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- num_loc (in)
- local number of the face
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < feval.GetM(); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
feval(i) = exp(-Dot(pt3D, pt3D));
feval(i) *= pyr.WeightsQuadratureBoundary(i, num_loc);
}
VectReal_wp res(pyr.GetNbDof());
// we want to compute the integral against basis functions
// the integral is made over a face
pyr.ComputeIntegralSurfaceRef(feval, res, num_loc);
Location :
FiniteElement/ElementReferenceBase.hxx
FiniteElement/ElementReferenceBase.cxx
GetValuePhiOnQuadraturePoint
Syntax
| void GetValuePhiOnQuadraturePoint(int k, Vector& phi) const |
This method computes the values of all basis functions on the k-th quadrature point (on the reference element) :
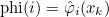
Parameters
- k (in)
- quadrature point number
- phi (out)
- values of basis functions
For scalar finite elements, the type of phi is VectReal_wp whereas it is VectR2 (VectR3 in 3-D) for vectorial finite elements
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we want to know phi_i(x_k) int k = 12; VectReal_wp phi; // use VectR2 or VectR3 for vectorial finite elements pyr.GetValuePhiOnQuadraturePoint(k, phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
GetGradientPhiOnQuadraturePoint
Syntax
| void GetGradientPhiOnQuadraturePoint(int k, Vector& grad_phi) const |
This method computes the gradient of all basis functions on the k-th quadrature point (on the reference element) :
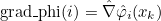
This method is available only for scalar finite elements. For edge elements, you can call GetCurlPhiOnQuadraturePoint. For facet elements, you can call GetDivPhiOnQuadraturePoint.
Parameters
- k (in)
- quadrature point number
- grad_phi (out)
- gradient of basis functions
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we want to know \nabla phi_i(x_k) int k = 12; VectR3 grad_phi; pyr.GetGradientPhiOnQuadraturePoint(k, grad_phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
GetCurlPhiOnQuadraturePoint
Syntax
| void GetGradientPhiOnQuadraturePoint(int k, Vector& curl_phi) const |
This method computes the curl of all basis functions on the k-th quadrature point (on the reference element) :
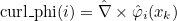
This method is available only for edge elements. For scalar elements, you can call GetGradientPhiOnQuadraturePoint. For facet elements, you can call GetDivPhiOnQuadraturePoint.
Parameters
- k (in)
- quadrature point number
- curl_phi (out)
- curl of basis functions
Example :
HexahedronHcurlFirstFamily hex; int order = 4; hex.ConstructFiniteElement(order); // we want to know curl(phi)_i(x_k) int k = 12; VectR3 curl_phi; hex.GetCurlPhiOnQuadraturePoint(k, curl_phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
GetDivPhiOnQuadraturePoint
Syntax
| void GetDivPhiOnQuadraturePoint(int k, VectReal_wp& div_phi) const |
This method computes the divergence of all basis functions on the k-th quadrature point (on the reference element) :
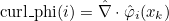
This method is available only for facet elements. For scalar elements, you can call GetGradientPhiOnQuadraturePoint. For edge elements, you can call GetCurlPhiOnQuadraturePoint.
Parameters
- k (in)
- quadrature point number
- div_phi (out)
- divergence of basis functions
Example :
HexahedronHdivFirstFamily hex; int order = 4; hex.ConstructFiniteElement(order); // we want to know div(phi)_i(x_k) int k = 12; VectReal_wp div_phi; hex.GetDivPhiOnQuadraturePoint(k, div_phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
GetValueSinglePhiQuadrature
Syntax
| void GetValueSinglePhiQuadrature(int i, VectReal_wp& phi) const |
This method computes the values of a single basis function on all the quadrature points (on the reference element) :
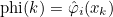
where xk are quadrature points on the reference element. This method is available only for scalar finite elements.
Parameters
- i (in)
- dof number
- phi (out)
- values of the selected basis function on quadrature points
Example :
HexahedronGauss hex; int order = 4; hex.ConstructFiniteElement(order); // we want to know phi_i(x_k) int i = 8; VectReal_wp phi; hex.GetValueSinglePhiQuadrature(i, phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
GetGradientSinglePhiQuadrature
Syntax
| void GetGradientSinglePhiQuadrature(int i, VectReal_wp& phi, VectR_N& grad_phi) const |
This method computes the values (ant its gradients) of a single basis function on all the quadrature points (on the reference element) :
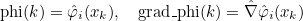
where xk are quadrature points on the reference element. This method is available only for scalar finite elements.
Parameters
- i (in)
- dof number
- phi (out)
- values of the selected basis function on quadrature points
- grad_phi (out)
- gradient of the selected basis function on quadrature points
Example :
HexahedronGauss hex; int order = 4; hex.ConstructFiniteElement(order); // we want to know phi_i(x_k) and \nabla phi_i(x_k) int i = 8; VectReal_wp phi; VectR3 grad_phi; hex.GetGradientSinglePhiQuadrature(i, phi, grad_phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
ComputeValuesPhiRef
Syntax
| void ComputeValuesPhiRef(const R_N& x, Vector& phi) const |
This method computes the values of all basis functions for the given point x :
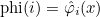
Parameters
- x (in)
- point where basis functions are evaluated
- phi (out)
- values of basis functions
For scalar finite elements, the type of phi is VectReal_wp whereas it is VectR2 (VectR3 in 3-D) for vectorial finite elements
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we want to know phi_i(x) R3 x(0.2, 0.3, 0.4); VectReal_wp phi; // use VectR2 or VectR3 for vectorial finite elements pyr.ComputeValuesPhiRef(x, phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
ComputeGradientPhiRef
Syntax
| void ComputeGradientPhiRef(const R_N& x, VectR_N& grad_phi) const |
This method computes the gradient of all basis functions for the given point x :
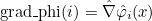
Parameters
- x (in)
- point where basis functions are evaluated
- grad_phi (out)
- gradient of basis functions
This method is available only for scalar finite elements. For edge elements, you can call ComputeCurlPhiRef. For facet elements, you can call ComputeDivPhiRef.
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we want to know grad(phi)_i(x) R3 x(0.2, 0.3, 0.4); VectR3 grad_phi; pyr.ComputeGradientPhiRef(x, grad_phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
ComputeCurlPhiRef
Syntax
| void ComputeCurlPhiRef(const R_N& x, Vector& curl_phi) const |
This method computes the curl of all basis functions for the given point x :
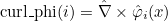
Parameters
- x (in)
- point where basis functions are evaluated
- curl_phi (out)
- curl of basis functions
This method is available only for edge elements. For scalar elements, you can call ComputeGradientPhiRef. For facet elements, you can call ComputeDivPhiRef.
Example :
HexahedronHcurlFirstFamily hex; int order = 4; hex.ConstructFiniteElement(order); // we want to know curl(phi)_i(x) R3 x(0.2, 0.3, 0.4); VectR3 curl_phi; hex.ComputeCurlPhiRef(x, curl_phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
ComputeDivPhiRef
Syntax
| void ComputeDivPhiRef(const R_N& x, VectReal_wp& div_phi) const |
This method computes the divergence of all basis functions for the given point x :
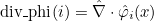
Parameters
- x (in)
- point where basis functions are evaluated
- div_phi (out)
- divergence of basis functions
This method is available only for facet elements. For scalar elements, you can call ComputeGradientPhiRef. For edge elements, you can call ComputeCurlPhiRef.
Example :
HexahedronHdivFirstFamily hex; int order = 4; hex.ConstructFiniteElement(order); // we want to know div(phi)_i(x) R3 x(0.2, 0.3, 0.4); VectR3 div_phi; hex.ComputeDivPhiRef(x, div_phi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
SetVariableOrder
Syntax
| void SetVariableOrder(const Mesh& mesh, const MeshNumbering& mesh_num) |
This method provides the mesh numbering to the finite element class such that interpolation needed for variable order is computed if needed. This method is useless is you have a fixed order for all the elements of the mesh.
Parameters
- mesh (in)
- working mesh
- mesh_num (in)
- working mesh numbering
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); HexahedronHdivFirstFamily hex; int order = 4; hex.ConstructFiniteElement(order); mesh_num.NumberMesh(); // if you want to compute interpolation operators for variable order : hex.SetVariableOrder(mesh, mesh_num);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
ComputeValuesPhiQuadratureRef
Syntax
| void ComputeValuesPhiQuadratureRef(const R_N& x, Vector& phi) const |
This method computes the values of all basis functions (associated with quadrature points) for the given point x :
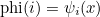
Parameters
- x (in)
- point where basis functions are evaluated
- phi (out)
- values of basis functions associated with quadrature points
This method is meaningful if quadrature points can be used to construct basis functions (mainly for quad/hexahedral elements).
Example :
HexahedronGauss hex; int order = 4; hex.ConstructFiniteElement(order); // we want to know psi_i(x) R3 x(0.2, 0.3, 0.4); VectReal_wp psi; hex.ComputeValuesPhiQuadratureRef(x, psi);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
FjSurfaceElem
Syntax
| void FjSurfaceElem( | const VectR_N& s, SetPoints& res, |
| Mesh& mesh, int num_elem, int num_loc) const |
This method fills the object res with quadrature points of the boundary num_loc of element num_elem. This method should be called after a call to FjElem or FjElemQuadrature.
Parameters
- s (in)
- vertices of the element
- res (out)
- object that will store the computed quadrature points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
- num_loc (in)
- local edge (face in 3-D) number
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
HexahedronGauss hex;
int order = 4;
hex.ConstructFiniteElement(order);
hex.SetMesh(mesh);
// computing quadrature points on a given element
int num_elem = 30;
VectR3 s; mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> PointsElem;
hex.FjElemQuadrature(s, PointsElem, mesh, num_elem);
// then we extract points on a boundary of the element
int num_loc = 2;
hex.FjElemSurface(s, PointsElem, mesh, num_elem, num_loc);
// if you need to have coordinates of a single point :
R3 pt = PointsElem.GetPointQuadratureBoundary(3);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
DFjSurfaceElem
Syntax
| void DFjSurfaceElem( | const VectR_N& s, const SetPoints& PointsElem, SetMatrices& res, |
| const Mesh& mesh, int num_elem, int num_loc) const |
This method fills the object res with jacobian matrices, normales, surface element and curvatures for the quadrature points of the boundary num_loc of element num_elem. This method should be called after a call to DFjElem or DFjElemQuadrature. In 3-D, the curvatures are correctly computed if the boundary belongs to a curved surface (if the mesh file is curved, or if you provide a predefined curve in TypeCurve). In 2-D, the second curvature k2 is null except if you called the method SetAxisymmetricGeometry (called for axisymmetric problems).
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object that stores the computed quadrature points
- res (out)
- object that will store the computed jacobians on quadrature points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
- num_loc (in)
- local edge (face in 3-D) number
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
HexahedronGauss hex;
int order = 4;
hex.ConstructFiniteElement(order);
hex.SetMesh(mesh);
// computing quadrature points on a given element
int num_elem = 30;
VectR3 s; mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> PointsElem;
hex.FjElemQuadrature(s, PointsElem, mesh, num_elem);
// and jacobian matrices
SetMatrices<Dimension3> MatricesElem;
hex.DFjElemQuadrature(s, PointsElem, MatricesElem, mesh, num_elem);
// then we extract jacobian matrices on quadrature points of a boundary of the element
int num_loc = 2;
hex.DFjElemSurface(s, PointsElem, MatricesElem, mesh, num_elem, num_loc);
// you can access to the jacobian matrix, outgoing normale, surface element or curvatures
int num_point = 3;
Matrix3_3 dfj = MatricesElem.GetPointQuadratureBoundary(num_point);
R3 normale = MatricesElem.GetNormaleQuadratureBoundary(num_point);
Real_wp ds = MatricesElem.GetDsQuadratureBoundary(num_point);
// two curvatures k1 and k2
Real_wp k1 = MatricesElem.GetK1QuadratureBoundary(num_point);
Real_wp k2 = MatricesElem.GetK2QuadratureBoundary(num_point);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
FjSurfaceElemDof
Syntax
| void FjSurfaceElemDof( | const VectR_N& s, SetPoints& res, |
| Mesh& mesh, int num_elem, int num_loc) const |
This method fills the object res with dof points of the boundary num_loc of element num_elem. This method should be called after a call to FjElem or FjElemDof.
Parameters
- s (in)
- vertices of the element
- res (out)
- object that will store the computed dof points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
- num_loc (in)
- local edge (face in 3-D) number
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
HexahedronGauss hex;
int order = 4;
hex.ConstructFiniteElement(order);
hex.SetMesh(mesh);
// computing dof points on a given element
int num_elem = 30;
VectR3 s; mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> PointsElem;
hex.FjElemDof(s, PointsElem, mesh, num_elem);
// then we extract dof points on a boundary of the element
int num_loc = 2;
hex.FjElemSurfaceDof(s, PointsElem, mesh, num_elem, num_loc);
// if you need to have coordinates of a single point :
R3 pt = PointsElem.GetPointDofBoundary(3);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
DFjSurfaceElemDof
Syntax
| void DFjSurfaceElemDof( | const VectR_N& s, const SetPoints& PointsElem, SetMatrices& res, |
| const Mesh& mesh, int num_elem, int num_loc) const |
This method fills the object res with jacobian matrices for the dof points of the boundary num_loc of element num_elem. This method should be called after a call to DFjElem or DFjElemDof.
Parameters
- s (in)
- vertices of the element
- PointsElem (in)
- object that stores the computed dof points
- res (out)
- object that will store the computed jacobians on dof points
- mesh (in)
- mesh that contains the considered element
- num_elem (in)
- element number
- num_loc (in)
- local edge (face in 3-D) number
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
HexahedronGauss hex;
int order = 4;
hex.ConstructFiniteElement(order);
hex.SetMesh(mesh);
// computing dof points on a given element
int num_elem = 30;
VectR3 s; mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> PointsElem;
hex.FjElemDof(s, PointsElem, mesh, num_elem);
// and jacobian matrices
SetMatrices<Dimension3> MatricesElem;
hex.DFjElemDof(s, PointsElem, MatricesElem, mesh, num_elem);
// then we extract jacobian matrices on dof points of a boundary of the element
int num_loc = 2;
hex.DFjElemSurfaceDof(s, PointsElem, MatricesElem, mesh, num_elem, num_loc);
// you can access to the jacobian matrix
int num_point = 3;
Matrix3_3 dfj = MatricesElem.GetPointDofBoundary(num_point);
Location :
FiniteElement/ElementReference.hxx
FiniteElement/ElementReference.cxx
PointsQuadInsideND
Syntax
| VectR_N PointsQuadInsideND(int N) const |
This method returns the quadrature points on the reference element. The parameter N is the number of quadrature points to extract.
Example :
TriangleGeomReference tri; int order = 4; tri.ConstructFiniteElement(order); // we want to retrieve the first four quadrature points VectR2 xvec = tri.PointsQuadInsideND(4);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
PointsQuadInsideND
Syntax
| VectR_N PointsQuadInsideND() const |
This method returns the quadrature points on the reference element. The parameter N is the number of quadrature points to extract.
Example :
TriangleClassical tri; int order = 4; tri.ConstructFiniteElement(order); // we want to retrieve the quadrature points for integrals over the triangle VectR2 pts = tri.PointsQuadInsideND();
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
GetNbPointsNodalElt
Syntax
| int GetNbPointsNodalElt() const |
This method returns the number of nodal points of the reference element.
Example :
TriangleGeomReference tri; int order = 4; tri.ConstructFiniteElement(order); // how many nodal points on the triangle ? int N = tri.GetNbPointsNodalElt();
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetNbNodalBoundary
Syntax
| int GetNbNodalBoundary(int num_loc) const |
This method returns the number of nodal points located on the face (edge in 2-D) num_loc.
Example :
PyramidGeomReference pyr; int order = 4; pyr.ConstructFiniteElement(order); // how many nodal points on a face of the pyramid int nb_nodes_quad = pyr.GetNbNodalBoundary(0); // first face is a quad int nb_nodes_tri = pyr.GetNbNodalBoundary(1); // other faces are triangles
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetNumNodes2D, GetNumNodes3D
Syntax
| int GetNumNodes2D(int i, int j) const |
| const Matrix<int>& GetNumNodes2D() const |
| const Matrix<int>& GetCoordinateNodes2D() const |
| int GetNumNodes3D(int i, int j, int k) const |
| const Array3D<int>& GetNumNodes3D() const |
| const Matrix<int>& GetCoordinateNodes3D() const |
The method GetNumNodes2D returns the node number from its position (i, j) in 2-D. If no argument is provided, it returns directly the matrix containing the node numbers. The method GetNumNodes3D is available in 3-D only and returns the node number from its position (i, j, k). The method GetCoordinateNodes2D (GetCoordinateNodes3D in 3-D) returns the reciprocal array, to know the position (i, j) of a node from its number.
Example :
int order = 4; TriangleGeomReference tri; tri.ConstructFiniteElement(order); int node12 = tri.GetNumNodes2D(1, 2); // to get all the numbers : const Matrix<int>& node_num = tri.GetNumNodes2D(); // position of node 13 : int i = tri.GetCoordinateNodes2D()(13, 0); int j = tri.GetCoordinateNodes2D()(13, 1); // 3-D example HexahedronGeomReference hex; hex.ConstructFiniteElement(order); int node102 = hex.GetNumNodes3D(1, 0, 2); const Array3D<int>& node_hex = hex.GetNumNodes3D(); // position of node 13 : i = hex.GetCoordinateNodes3D()(13, 0); j = hex.GetCoordinateNodes3D()(13, 1); int k = hex.GetCoordinateNodes3D()(13, 2);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
PointsNodalBoundary
Syntax
| Real_wp PointsNodalBoundary(int i, int num_loc) const |
This method returns the i-th nodal point of the boundary num_loc. This point is a 1-D nodal point (2-D point in 3-D) and not a point on the reference element. To obtain the point on the reference element, you can call GetLocalCoordOnBoundary.
Example :
int order = 4; TriangleGeomReference tri; tri.ConstructFiniteElement(order); int num_loc = 1; Real_wp x = tri.PointsNodalBoundary(2, num_loc); // 1-D nodal point // to get coordinates in the reference element R2 point; tri.GetLocalCoordOnBoundary(num_loc, x, point); // 3-D example HexahedronGeomReference hex; hex.ConstructFiniteElement(order); R2 pt2D = hex.PointsNodalBoundary(2, num_loc); // to get coordinates in the reference element R3 point3D; hex.GetLocalCoordOnBoundary(num_loc, pt2D, point3D);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetNodalNumber
Syntax
| int GetNodalNumber(int num_loc, int i) const |
This method returns the i-th nodal point number of the boundary num_loc.
Example :
int order = 4; TriangleGeomReference tri; tri.ConstructFiniteElement(order); int num_loc = 1; int i = 3; int n = tri.GetNodalNumber(num_loc, i); // to get coordinates in the reference element R2 point = tri.PointsNodalND(n); // 3-D example HexahedronGeomReference hex; hex.ConstructFiniteElement(order); n = hex.GetNodalNumber(num_loc, i); // to get coordinates in the reference element R3 point3D = hex.PointsNodalND(n);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
PointsND
Syntax
| R_N PointsND(int i) const |
| const VectR_N& PointsND() const |
This method returns the i-th quadrature point of the reference element. In the second syntax, you can retrieve all the quadrature points.
Example :
int order = 4; TriangleClassical tri; tri.ConstructFiniteElement(order); // a single quadrature point R2 pt = tri.PointsND(3); // or all the quadrature points const VectR2& all_pts = tri.PointsND(); // 3-D example HexahedronGauss hex; hex.ConstructFiniteElement(order); // a single quadrature point R3 point = hex.PointsND(3); // or all the quadrature points const VectR3& all_pts_3d = hex.PointsND();
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
PointsQuadND
Syntax
| VectR_N PointsQuadND() const |
This method returns the quadrature points of the reference element. The difference with PointsND is that the quadrature points of the boundaries are placed after quadrature points for volume integrals even though some quadrature points may coincide (for instance with Gauss-Lobatto points). As a result, the returned array can contain duplicate points, whereas PointsND should return an array without duplicates.
Example :
int order = 4; TriangleClassical tri; tri.ConstructFiniteElement(order); // all the quadrature points (interior and boundaries after) VectR2 all_pts = tri.PointsQuadND(); // 3-D example HexahedronLobatto hex; hex.ConstructFiniteElement(order); VectR3 all_pts3d = hex.PointsQuadND();
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
PointsDofBoundary
Syntax
| const VectR_Nm1& PointsDofBoundary(int num_loc) const |
This method returns the dof points of the boundary num_loc. These dof points are 1-D coordinates for 2-D finite elements and 2-D points for 3-D finite elements. They can be used to compute the projection on trace finite element. To obtain the coordinates on the reference element, the method GetLocalCoordOnBoundary can be used.
Example :
int order = 4; TriangleClassical tri; tri.ConstructFiniteElement(order); // dof points for an edge const VectReal_wp& dof_pts1d = tri.PointsDofBoundary(0); // 3-D example PyramidClassical pyr; pyr.ConstructFiniteElement(order); // dof points for a face const VectR2& dof_pts2d = pyr.PointsDofBoundary(0);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
PointsQuadratureBoundary
Syntax
| const VectR_Nm1& PointsQuadratureBoundary(int num_loc) const |
| const R_Nm1& PointsQuadratureBoundary(int k, int num_loc) const |
This method returns the quadrature points of the boundary num_loc. These quadrature points are 1-D coordinates for 2-D finite elements and 2-D points for 3-D finite elements. To obtain the coordinates on the reference element, the method GetLocalCoordOnBoundary can be used. In the second syntax, you can retrieve a single quadrature point.
Example :
int order = 4; TriangleClassical tri; tri.ConstructFiniteElement(order); // quadrature points for an edge int num_loc = 1; const VectReal_wp& quad_pts1d = tri.PointsQuadratureBoundary(num_loc); // single point int k = 3; Real_wp x = tri.PointsQuadratureBoundary(k, num_loc); // 3-D example PyramidClassical pyr; pyr.ConstructFiniteElement(order); // quadrature points for a face const VectR2& quad_pts2d = pyr.PointsQuadratureBoundary(num_loc); // single point R2 pt = pyr.PointsQuadratureBoundary(k, num_loc);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
WeightsQuadratureBoundary
Syntax
| const VectReal_wp& WeightsQuadratureBoundary(int num_loc) const |
| const Real_wp& WeightsQuadratureBoundary(int k, int num_loc) const |
This method returns the quadrature weights of the boundary num_loc. These quadrature weights can be used for 1-D integrals over unit interval for 2-D finite elements.For 3-D finite elements, they can be used for an integral over the unit square (if the face num_loc is a quadrilateral) or the unit triangle (if the face num_loc is a triangle). In the second syntax, you can retrieve a single quadrature weight.
Example :
int order = 4; TriangleClassical tri; tri.ConstructFiniteElement(order); // quadrature weights for unit interval int num_loc = 1; const VectReal_wp& quad_weights1d = tri.WeightsQuadratureBoundary(num_loc); // single weight int k = 3; Real_wp w = tri.WeightsQuadratureBoundary(k, num_loc); // 3-D example PyramidClassical pyr; pyr.ConstructFiniteElement(order); // quadrature weights for unit triangle (face 1 is a triangle) const VectReal_wp& quad_wts2d = pyr.WeightsQuadratureBoundary(num_loc); // single weight w = pyr.WeightsQuadratureBoundary(k, num_loc);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetNbPointsDof
Syntax
| int GetNbPointsDof() const |
This method returns the number of dof points (interior + boundary). These dof points are points associated with degrees of freedom, and are used to project a function in the finite element basis (boundary dof points can be used to project on the surface finite element).
Example :
int order = 4; TriangleClassical tri; tri.ConstructFiniteElement(order); // total number of dof points int N = tri.GetNbPointsDof();
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
PointsDofND
Syntax
| const VectR_N& PointsDofND() const |
| const R_N& PointsDofND(int i) const |
This method returns the coordinates of the i-th dof point. You can also retrieve all the dof points. These dof points are points associated with degrees of freedom, and are used to project a function in the finite element basis.
Example :
int order = 4; TriangleClassical tri; tri.ConstructFiniteElement(order); // evaluation of a function on dof points VectReal_wp feval(tri.GetNbPointsDofInside()); for (int i = 0; i < tri.GetNbPointsDofInside(); i++) feval(i) = exp(-Norm(tri.PointsDofND(i))); // then projection on finite element basis VectReal_wp u; tri.ComputeProjectionDofRef(feval, u); // you can also retrieve all the dof points const VectR2& pts = tri.PointsDofND();
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetNbPointsQuadrature
Syntax
| int GetNbPointsQuadrature() const |
This method returns the number of integration points used for volume or surface integrals. The points can be accessed with the method PointsND, and weights with the method WeightsND.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // should return 4^3 (3-D) + 6*4^2 (for faces) = 160 int nb_quad = hex.GetNbPointsQuadrature(); // hex.GetNbPointsQuadratureInside() will return 64 (points for 3-D integrals only)
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetNbQuadBoundary
Syntax
| int GetNbQuadBoundary(int num_loc) const |
This method returns the number of integration points used for surface integral over the face (edge in 2-D) num_loc.
Example :
HexahedronGauss hex;
hex.ConstructFiniteElement(3);
// we want to compute a surface integral \int_{\partial_j K} f(x) \hat{\varphi}_i(x) dx
int num_loc = 2;
int nb_quad = hex.GetNbQuadBoundary(num_loc);
// evaluation of the function f = exp(-|| x ||) on quadrature points
VectReal_wp feval(nb_quad);
// here num = hex.GetQuadNumber(num_loc, i) is the quadrature point number
// PointsND(num) will be the coordinates of this point
for (int i = 0; i < nb_quad; i++)
feval(i) = exp(-Norm2(hex.PointsND(hex.GetQuadNumber(num_loc, i))))
*hex.WeightsQuadratureBoundary(i, num_loc);
// computation of the surface integral
VectReal_wp u;
hex.ComputeIntegralSurfaceRef(feval, u, num_loc);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetLocalCoordOnBoundary
Syntax
| void GetLocalCoordOnBoundary(int num_loc, const R2& pt_loc, R3& point) const |
| void GetLocalCoordOnBoundary(int num_loc, const R3& point, R2& pt_loc) const |
This method computes the coordinates of point from the local position on the face num_loc. In the second syntax, the reciprocal operation is performed : local position is filled from coordinates on the reference element.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // local position of a point on the face R2 pt_loc(0.2, 0.5); // coordinates on the reference element int num_loc = 1; // face number R3 point; hex.GetLocalCoordOnBoundary(num_loc, pt_loc, point); // point should be equal to (0.2, 0.0, 0.5) for this example // you can perform the reciprocal operation R2 pt_loc2; hex.GetLocalCoordOnBoundary(num_loc, point, pt_loc2); // pt_loc2 should be equal to (0.2, 0.5) for this example // example in 2-D TriangleClassical tri; tri.ConstructFiniteElement(3); // local position of a point on the edge Real_wp xloc = 0.3; // coordinates on the reference element num_loc = 1; // edge number R2 point_tri; tri.GetLocalCoordOnBoundary(num_loc, xloc, point_tri); // point should be equal to (0.7, 0.3) for this example // you can perform the reciprocal operation Real_wp xloc2; tri.GetLocalCoordOnBoundary(num_loc, point_tri, xloc2); // xloc2 should be equal to 0.3 for this example
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetBoundingBox
Syntax
| static void GetBoundingBox(const VectR_N& s, const Real_wp& coef, VectR_N& polygon, TinyVector<R_N, 2>& box) |
This method computes the bounding box containing the element defined by its vertices s. box is a bounding polygon, enveloppe the bounding box, and coef is a safety coefficient (which can be used for curved elements for example).
Parameters
- s (in)
- vertices of the element
- coef (in)
- safety coefficient (for curved elements)
- polygon (out)
- polygonal enveloppe
- box (out)
- rectangular bounding box
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// bounding box of element 18 ?
VectR3 s;
int n = 18;
mesh.GetVerticesElement(n, s);
// estimating the bounding box with a safety coefficient of 10%
// you can put 0 if the element is straight
VectR3 box(s.GetM());
TinyVector<R3, 2> enveloppe;
ElementGeomReference<Dimension3>::GetBoundingBox(s, 0.1, box, enveloppe);
cout << "the element is included in box " << "[" << enveloppe(0)(0) << "," << enveloppe(1)(0) << "] x ["
<< enveloppe(0)(1) << "," << enveloppe(1)(1) << "] x ["
<< enveloppe(0)(2) << "," << enveloppe(1)(2) << " ]" << endl;
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
IsAffineTransformation
Syntax
| static bool IsAffineTransformation(const VectR_N& s) |
This method returns true if the transformation Fi that transforms the reference element to the given element is affine. If this transformation is affine, it can be written as
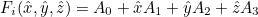
in 3-D. Triangles/tetrahedra always conduct to an affine transformation. For quadrilaterals, only parallelograms conduct to an affine transformation.
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// vertices of an element
int n = 18; VectR3 s;
mesh.GetVerticesElement(n, s);
// Fi is affine for this element ?
bool affine = ElementGeomReference<Dimension3>::IsAffineTransformation(s);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetCurvatureNodal
Syntax
| static void GetCurvatureNodal(const Globatto& lob, const VectR2& normale, const VectReal_wp& ds, VectReal_wp& h) |
This method computes the curvatures for nodal points (local abscissae are given by lob.Points) from normale and lineic elements. This method is available only in 2-D. On a regular use, if you need curvatures on the quadrature points, the best is to call DFjSurfaceElem, which computes the curvatures in 2-D or 3-D.
Parameters
- lob (in)
- local position of nodal points
- normale (in)
- outgoing normale for nodal points
- ds (in)
- lineic element
- h (out)
- curvatures for nodal points
Example :
Globatto<Real_wp> lob;
lob.ConstructQuadrature(3, lob.QUADRATURE_LOBATTO);
// normales and lineic element on Gauss-Lobatto points
VectR2 normale(4); VectReal_wp ds(4);
for (int i = 0: i < 4; i++)
{
Real_wp teta = lob.Points(i);
normale(i).Init(cos(teta), sin(teta));
ds(i) = 1.0;
}
// h will contain the curvatures for Gauss-Lobatto points (here h should be filled with ones since we chose a circle of radius 1)
VectReal_wp h;
ElementGeomReference<Dimension2>GetCurvatureNodal(lob, normale, ds, h);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetNodalShapeFunctions1D
Syntax
| const Globatto<Real_wp>& GetNodalShapeFunctions1D() |
This method returns the object storing 1-D shape functions based on the nodal points (usually Gauss-Lobatto points).
Example :
TriangleClassical tri; tri.ConstructFiniteElement(3); // retrieving 1-D shape functions (on the unit interval) const Globatto<Real_wp>& lob = tri.GetNodalShapeFunctions1D(); // then you can use the object to evaluate shape functions for example VectReal_wp phi; lob.ComputeValuesPhiRef(Real_wp(0.4), phi);
Location :
FiniteElement/FaceGeomReference.hxx
FiniteElement/FaceGeomReference.cxx
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
IsLocalFaceQuadrilateral
Syntax
| bool IsLocalFaceQuadrilateral(int num_loc) const |
This method returns true if the face num_loc is a quadrilateral. It is relevant only for 3-D finite elements.
Example :
WedgeGeomReference elt; // face 1 is a quadrangle ? bool quad = elt.IsLocalFaceQuadrilateral(1);
Location :
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
TangenteLocX, TangenteLocY
Syntax
| const R3& TangenteLocX(int num_loc) const |
| const R3& TangenteLocY(int num_loc) const |
These methods return two tangent vectors of the face num_loc (of the reference element). It is available only for 3-D finite elements.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(4); // tangent vectors of face 4 R3 u = pyr.TangenteLocX(4); R3 v = pyr.TangenteLocY(4);
Location :
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetTangentialVector, TransposeTangentialVector
Syntax
| const R3& GetTangentialVector(int num_loc, const R2& u) const |
| const R2& TransposeTangentialVector(int num_loc, const R3& v) const |
The method GetTangentialVector returns a 3-D tangential vector for the face num_loc from a 2-D vector (on the unit square for quadrilateral faces, the unit triangle for triangular faces). The method TransposeTangentialVector is the reciprocal function.
Example :
PyramidClassical pyr; pyr.ConstructFiniteElement(4); // 3-D tangent vector for face 2 R2 u(0.8, 0.6); R3 v = pyr.GetTangentialVector(2, u); // recovering u from v : u = pyr.TransposeTangentialVector(2, v);
Location :
FiniteElement/VolumeGeomReference.hxx
FiniteElement/VolumeGeomReference.cxx
GetLocalNumber
Syntax
| int GetLocalNumber(int num_loc, int i) const |
This method returns the dof number of the i-th degree of freedom of the face num_loc.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // dof i of face num_loc int num_loc = 1; int i = 5; int num_dof = hex.GetLocalNumber(num_loc, i);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
GetNbDofBoundary
Syntax
| int GetNbDofBoundary(int num_loc) const |
This method returns the number of degrees of freedom associated with the face num_loc.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(3); // number of dofs for face 2 ? int nb_dof = hex.GetNbDofBoundary(2);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ProjectQuadratureToDofRef
Syntax
| void ProjectQuadratureToDofRef(const Vector& u_quad, Vector& u) const |
This method projects a field on the finite element basis from values on quadrature points.
Parameters
- u_quad (in)
- values of u on quadrature points
- u (inout)
- components of u on degrees of freedom (allocated on input)
Example :
HexahedronHcurlFirstFamily hex;
hex.ConstructFiniteElement(3);
// field on quadrature points
// exemple : f = (sin(x), cos(yz), exp(-x-z))
VectReal_wp u_quad(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
Real_wp x = hex.PointsND(i)(0), y = hex.PointsND(i)(1), z = hex.PointsND(i)(2);
u_quad(3*i) = sin(x); u_quad(3*i+1) = cos(y*z); u_quad(3*i+2) = exp(-x-z);
}
// projection on degrees of freedom
VectReal_wp u(hex.GetNbDof());
hex.ProjectQuadratureToDofRef(u_quad, u);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ComputeLocalProlongationLowOrder
Syntax
| void ComputeLocalProlongationLowOrder(const ElementReference& elt_coarse, Matrix<Real_wp>& P) const |
This method computes a prolongation operator that can be used to project a field defined on the coarse element to a field defined on the fine element (i.e. current element). This prolongation is computed by considering a subdivided mesh of the coarse element such that each basis function of the coarse element is seen as a first order basis function for the sub-element. With this approach; the prolongation operator is sparser than by calling ComputeLocalProlongation.
Parameters
- elt_coarse (in)
- coarse finite element
- P (out)
- prolongation matrix
Example :
HexahedronHcurlFirstFamily hex_fine; hex_fine.ConstructFiniteElement(4); HexahedronHcurlFirstFamily hex_coarse; hex_coarse.ConstructFiniteElement(2); // sparse prolongation operator Matrix<Real_wp> P; hex_fine.ComputeLocalProlongationLowOrder(hex_coarse, P);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ComputeNodalValuesRef
Syntax
| void ComputeNodalValuesRef(const Vector& u, Vector& u_nodal) const |
This method computes the values of a field on nodal points of the reference element from components on degrees of freedom.
Parameters
- u (in)
- components of u on degrees of freedom
- u_nodal (out)
- values of u on nodal points
Example :
HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(4); // starting from a random vector VectReal_wp u(hex.GetNbDof()); u.FillRand(); // projection on nodal points VectReal_wp u_nodal; hex.ComputeNodalValuesRef(u, u_nodal); int num_pt = 3; R3 vec_u; vec_u.Init(u_nodal(3*num_pt), u_nodal(3*num_pt+1), u_nodal(3*num_pt+2));
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ComputeProjectionPointsSurf
Syntax
| void ComputeProjectionPointsSurf(int num_loc, const VectR_Nm1& pts_source, const VectR_Nm1& pts_destination, Matrix<Real_wp>& P) const |
This method computes a projection operator to interpolate a scalar field defined on pts_source to a scalar field defined on pts_destination. It is currently implemented for the specific where there are more source points than destination points.
Parameters
- num_loc (in)
- local number of the face
- pts_source (in)
- source points
- pts_destination (in)
- destination points
- P (out)
- projection matrix
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(4); int m = 10; VectR2 pts_source(m); pts_source(0).Init(0.0, 0.0); pts_source(1).Init(1.0, 0.0); // etc int n= 4; VectR2 pts_dest(n); pts_dest(0).Init(0.2, 0.2); pts_dest(1).Init(0.8, 0.2); // etc int num_loc = 2; Matrix<Real_wp> P; hex.ComputeProjectionPointsSurf(num_loc, pts_source, pts_dest, P); // then if you know a field on pts_source : VectReal_wp u(pts_source.GetM()); u.FillRand(); // you can interpolate i to pts_dest : VectReal_wp u_dest(pts_source.GetM()); Mlt(P, u, u_dest);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ComputeVariableInterpolation
Syntax
| void ComputeVariableInterpolation(int rmax, const VectBool& order_present) |
This method computes the interpolation needed for variable order. This interpolation step is performed when you call ApplySh or ApplyShTranspose. Usually the method should be called to compute the present orders and construct associated interpolators. In this method, you provide directly the orders that are present (without giving the mesh). This method is present only for 2-D finite elements.
Parameters
- rmax (in)
- maximal order
- order_present (in)
- if order_present(i) is true, a interpolation towards finite element of order i is constructed and stored
Example :
QuadrangleGauss quad; quad.ConstructFiniteElement(4); // we want to construct interpolation with order 3 and 5 int rmax = 8; VectBool order_present(rmax+1); order_present.Fill(false); order_present(5) = true; order_present(3) = true; quad.ComputeVariableInterpolation(rmax, order_present);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
ComputeIntegralGradientRef
Syntax
| void ComputeIntegralGradientRef(const Vector& feval, Vector& res) const |
This method is actually equivalent to the method ApplyRh. It computes the integral against the gradient of basis functions
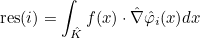
where f is a given function and φi are basis functions. The resulting vector is equal to
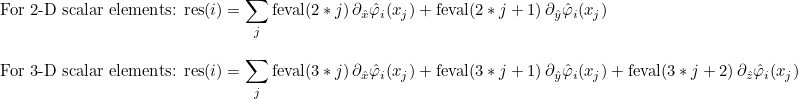
where xi are quadrature points of the reference element.
Parameters
- feval (in)
- Evaluation of f on quadrature points (multiplied by weights)
- res (inout)
- resulting vector (allocated on input)
This function is only available for scalar finite elements.
Example :
HexahedronLobatto hex;
int order = 4;
hex.ConstructFiniteElement(order);
// function to evaluate f = (-y^2, z^2, x*y)
VectReal_wp feval(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
Real_wp x = hex.PointsND(i)(0), y = hex.PointsND(i)(1), z = hex.PointsND(i)(2);
Real_wp poids = hex.WeightsND(i);
feval(3*i) = -y*y*poids; feval(3*i+1) = z*z*poids; feval(3*i+2) = x*y*poids;
}
// integration against gradient of basis functions
VectReal_wp res(hex.GetNbDof());
hex.ComputeIntegralGradientRef(feval, res);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeIntegralCurlRef
Syntax
| void ComputeIntegralCurlRef(const Vector& feval, Vector& res) const |
This method is actually equivalent to the method ApplyRh. It computes the integral against the curl of basis functions
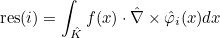
where f is a given function and φi are basis functions. The resulting vector is equal to
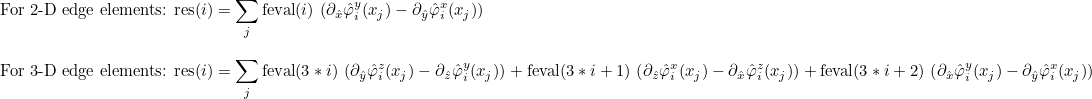
where xi are quadrature points of the reference element.
Parameters
- feval (in)
- Evaluation of f on quadrature points (multiplied by weights)
- res (inout)
- resulting vector (allocated on input)
This function is only available for edge elements.
Example :
HexahedronHcurlFirstFamily hex;
int order = 4;
hex.ConstructFiniteElement(order);
// function to evaluate f = (-y^2, z^2, x*y)
VectReal_wp feval(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
Real_wp x = hex.PointsND(i)(0), y = hex.PointsND(i)(1), z = hex.PointsND(i)(2);
Real_wp poids = hex.WeightsND(i);
feval(3*i) = -y*y*poids; feval(3*i+1) = z*z*poids; feval(3*i+2) = x*y*poids;
}
// integration against curl of basis functions
VectReal_wp res(hex.GetNbDof());
hex.ComputeIntegralCurlRef(feval, res);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeIntegralDivRef
Syntax
| void ComputeIntegralDivRef(const Vector& feval, Vector& res) const |
This method is actually equivalent to the method ApplyRh. It computes the integral against the divergence of basis functions
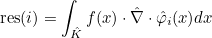
where f is a given function and φi are basis functions. The resulting vector is equal to
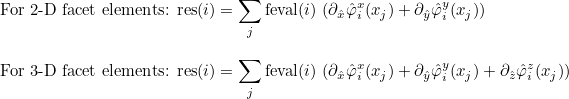
where xi are quadrature points of the reference element.
Parameters
- feval (in)
- Evaluation of f on quadrature points (multiplied by weights)
- res (inout)
- resulting vector (allocated on input)
This function is only available for facet elements.
Example :
HexahedronHdivFirstFamily hex;
int order = 4;
hex.ConstructFiniteElement(order);
// function to evaluate f = x*y*z
VectReal_wp feval(hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
Real_wp x = hex.PointsND(i)(0), y = hex.PointsND(i)(1), z = hex.PointsND(i)(2);
Real_wp poids = hex.WeightsND(i);
feval(i) = poids*x*y*z;
}
// integration against divergence of basis functions
VectReal_wp res(hex.GetNbDof());
hex.ComputeIntegralDivRef(feval, res);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeIntegralSurfaceGradientRef
Syntax
| void ComputeIntegralSurfaceGradientRef(const Vector& feval, Vector& res, int num_loc) const |
This method is similar to the method ApplyNablaSh. It computes the boundary integral against the gradient basis functions:
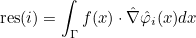
where f is a given function and φi are basis functions. Since weights are included in input vector feval, the resulting vector is equal to
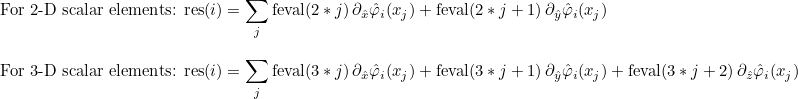
where xi are quadrature points of the face num_loc of the reference element.
Parameters
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- num_loc (in)
- local number of the face (edge in 2-D)
This function is only available for scalar finite elements.
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f = (cos(x+y), sin(z), exp(x-z)) on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < feval.GetM(); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
Real_wp x = pt3D(0), y = pt3D(1), z = pt3D(2);
Real_wp w = pyr.WeightsQuadratureBoundary(i, num_loc);
feval(3*i) = w*cos(x+y); feval(3*i+1) = w*sin(z); feval(3*i+2) = w*exp(x-z);
}
VectReal_wp res(pyr.GetNbDof());
// we want to compute the integral against gradient of basis functions
// the integral is made over a face
pyr.ComputeIntegralSurfaceGradientRef(feval, res, num_loc);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeIntegralSurfaceCurlRef
Syntax
| void ComputeIntegralSurfaceCurlRef(const Vector& feval, Vector& res, int num_loc) const |
This method is similar to the method ApplyNablaSh. It computes the boundary integral against the curl of basis functions:
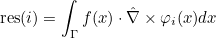
where f is a given function and φi are basis functions. Since weights are included in input vector feval, the resulting vector is equal to
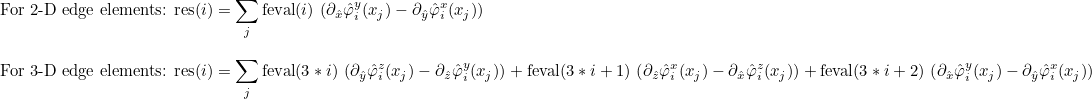
where xi are quadrature points of the face num_loc of the reference element.
Parameters
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- num_loc (in)
- local number of the face (edge in 2-D)
This function is only available for edge elements.
Example :
PyramidHcurlFirstFamily pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f = (cos(x+y), sin(z), exp(x-z)) on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < feval.GetM(); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
Real_wp x = pt3D(0), y = pt3D(1), z = pt3D(2);
Real_wp w = pyr.WeightsQuadratureBoundary(i, num_loc);
feval(3*i) = w*cos(x+y); feval(3*i+1) = w*sin(z); feval(3*i+2) = w*exp(x-z);
}
VectReal_wp res(pyr.GetNbDof());
// we want to compute the integral against curl of basis functions
// the integral is made over a face
pyr.ComputeIntegralSurfaceCurlRef(feval, res, num_loc);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeIntegralSurfaceDivRef
Syntax
| void ComputeIntegralSurfaceDivRef(const Vector& feval, Vector& res, int num_loc) const |
This method is similar to the method ApplyNablaSh. It computes the boundary integral against the divergence of basis functions:
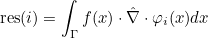
where f is a given function and φi are basis functions. Since weights are included in input vector feval, the resulting vector is equal to
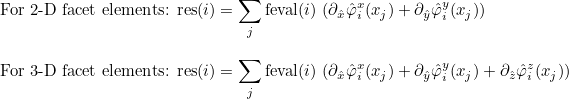
where xi are quadrature points of the face num_loc of the reference element.
Parameters
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
- num_loc (in)
- local number of the face (edge in 2-D)
This function is only available for facet elements.
Example :
PyramidHdivFirstFamily pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f = cos(x+y-z) on quadrature points of a face
int num_loc = 4;
VectReal_wp feval(pyr.GetNbQuadBoundary(num_loc));
for (int i = 0; i < feval.GetM(); i++)
{
R2 pt = pyr.PointsQuadratureBoundary(i, num_loc);
R3 pt3D; pyr.GetLocalCoordOnBoundary(num_loc, pt, pt3D);
Real_wp x = pt3D(0), y = pt3D(1), z = pt3D(2);
Real_wp w = pyr.WeightsQuadratureBoundary(i, num_loc);
feval(i) = w*cos(x+y-z);
}
VectReal_wp res(pyr.GetNbDof());
// we want to compute the integral against divergence of basis functions
// the integral is made over a face
pyr.ComputeIntegralSurfaceDivRef(feval, res, num_loc);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeValueBoundaryRef
Syntax
| void ComputeValueBoundaryRef(const Vector& u, Vector& u_nodal, int num_loc) const |
This method computes the values of a field on nodal points of the face num_loc of the reference element from components on degrees of freedom.
Parameters
- u (in)
- components of u on degrees of freedom
- u_nodal (out)
- values of u on nodal points of the face
- num_loc (in)
- local number of the face (edge in 2-D)
Example :
HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(4); // starting from a random vector VectReal_wp u(hex.GetNbDof()); u.FillRand(); // projection on nodal points of a face int num_loc = 2; // face number VectReal_wp u_nodal; hex.ComputeValueBoundaryRef(u, u_nodal, num_loc); int num_pt = 3; R3 vec_u; vec_u.Init(u_nodal(3*num_pt), u_nodal(3*num_pt+1), u_nodal(3*num_pt+2));
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ComputeGradientBoundaryRef
Syntax
| void ComputeGradientBoundaryRef(const Vector& u, Vector& grad_u_nodal, int num_loc) const |
This method computes the gradient of a field on nodal points of the face num_loc of the reference element from components on degrees of freedom.
Parameters
- u (in)
- components of u on degrees of freedom
- grad_u_nodal (out)
- gradient of u on nodal points of the face
- num_loc (in)
- local number of the face (edge in 2-D)
This method is available only for scalar finite elements.
Example :
HexahedronLobatto hex; hex.ConstructFiniteElement(4); // starting from a random vector VectReal_wp u(hex.GetNbDof()); u.FillRand(); // projection on nodal points of a face int num_loc = 2; // face number VectReal_wp grad_u_nodal; hex.ComputeGradientBoundaryRef(u, grad_u_nodal, num_loc); int num_pt = 3; R3 vec_u; vec_u.Init(grad_u_nodal(3*num_pt), grad_u_nodal(3*num_pt+1), grad_u_nodal(3*num_pt+2));
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ComputeCurlBoundaryRef
Syntax
| void ComputeCurlBoundaryRef(const Vector& u, Vector& curl_u_nodal, int num_loc) const |
This method computes the curl of a field on nodal points of the face num_loc of the reference element from components on degrees of freedom.
Parameters
- u (in)
- components of u on degrees of freedom
- curl_u_nodal (out)
- curl of u on nodal points of the face
- num_loc (in)
- local number of the face (edge in 2-D)
This method is available only for edge elements.
Example :
HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(4); // starting from a random vector VectReal_wp u(hex.GetNbDof()); u.FillRand(); // projection on nodal points of a face int num_loc = 2; // face number VectReal_wp curl_u_nodal; hex.ComputeCurlBoundaryRef(u, curl_u_nodal, num_loc); int num_pt = 3; R3 vec_u; vec_u.Init(curl_u_nodal(3*num_pt), curl_u_nodal(3*num_pt+1), curl_u_nodal(3*num_pt+2));
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ComputeDivBoundaryRef
Syntax
| void ComputeDivBoundaryRef(const Vector& u, Vector& div_u_nodal, int num_loc) const |
This method computes the divergence of a field on nodal points of the face num_loc of the reference element from components on degrees of freedom.
Parameters
- u (in)
- components of u on degrees of freedom
- div_u_nodal (out)
- divergence of u on nodal points of the face
- num_loc (in)
- local number of the face (edge in 2-D)
This method is available only for facet elements.
Example :
HexahedronHdivFirstFamily hex; hex.ConstructFiniteElement(4); // starting from a random vector VectReal_wp u(hex.GetNbDof()); u.FillRand(); // projection on nodal points of a face int num_loc = 2; // face number VectReal_wp div_u_nodal; hex.ComputeDivBoundaryRef(u, div_u_nodal, num_loc); int num_pt = 3; Real_wp div_pt = div_u_nodal(num_pt);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReferenceInline.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReferenceInline.cxx
ApplyRhTranspose
Syntax
| void ApplyRhTranspose(const Vector& u, Vector& res) const |
This method computes the gradient of a field on quadrature points of the reference element :
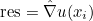
where xi are quadrature points of the reference element. The gradient is replaced by the curl for edge elements and by the divergence for facet elements. The resulting vector is equal to
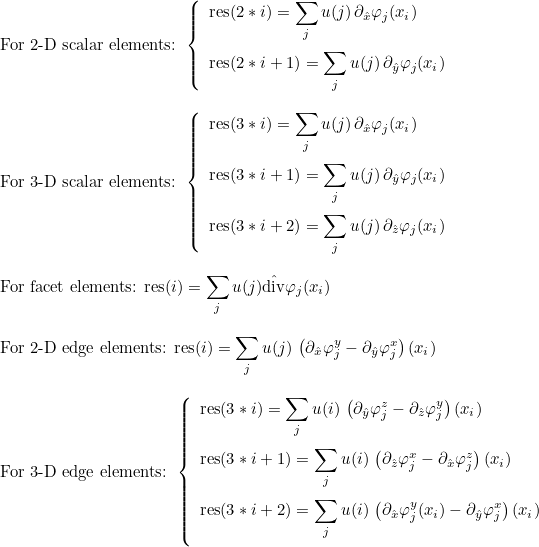
where φj are basis functions.
Parameters
- u (in)
- field u
- res (inout)
- resulting vector (allocated on input)
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we start from a field u (components on basis functions) VectReal_wp u(pyr.GetNbDof()); u.FillRand(); // we want to know gradient of u for quadrature points int num_loc = 3; VectReal_wp gradu_quad(3*pyr.GetNbPointsQuadratureInside()); pyr.ApplyRhTranspose(u, gradu_quad);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ApplyRh
Syntax
| void ApplyRh(const Vector& feval, Vector& res) const |
This method is the transpose operation of ApplyRh. It computes the integral against the gradient of basis functions:
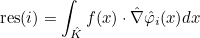
where f is a given function and φi are basis functions. The gradient is replaced by the curl for edge elements and by the divergence for facet elements. Since weights are included in input vector feval, the resulting vector is equal to
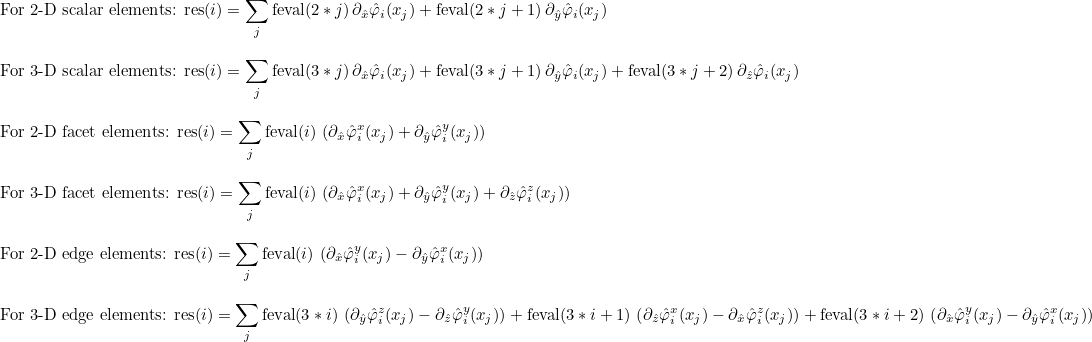
where xj are quadrature points.
Parameters
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- res (inout)
- resulting vector
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points
VectReal_wp feval(3*pyr.GetNbPointsQuadratureInside());
for (int i = 0; i < pyr.GetNbPointsQuadratureInside(); i++)
{
R3 pt3D = pyr.PointsND(i);
feval(3*i) = exp(-Dot(pt3D, pt3D));
feval(3*i) *= pyr.WeightsND(i);
feval(3*i+1) = exp(-Dot(pt3D, pt3D)*0.4);
feval(3*i+1) *= pyr.WeightsND(i);
feval(3*i+2) = exp(-Dot(pt3D, pt3D)*0.8);
feval(3*i+2) *= pyr.WeightsND(i);
}
VectReal_wp res(pyr.GetNbDof());
res.Zero();
// we want to compute the integral against gradient of basis functions
// the integral is made over the reference element
pyr.ApplyRh(feval, res);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ApplyRhSplit
Syntax
| void ApplyRhSplit(const Vector& feval, Vector& vx, Vector& vy) const |
This method is available only for scalar finite elements. It is similar to the method ApplyRh, but the result is split into two vectors (three in 3-D). It computes the integral against the derivatives of basis functions:
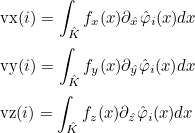
where f is a given function and φi are basis functions. Since weights are included in input vector feval, the resulting vector is equal to

where xj are quadrature points. The method ApplyRh actually computes res = vx + vy + vz (res = vx + vy in 2-D).
Parameters
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- vx (inout)
- integral against x-derivatives
- vy (inout)
- integral against y-derivatives
- vz (inout, 3D)
- integral against z-derivatives
Example :
HexahedronLobatto hex;
int order = 4;
hex.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points
VectReal_wp feval(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
R3 pt3D = hex.PointsND(i); Real_wp w = hex.WeightsND(i);
Real_wp x = pt3D(0), y = pt3D(1), z = pt3D(2);
feval(3*i) = w*exp(-x+y);
feval(3*i+1) = w*cos(x*z);
feval(3*i+2) = w*sin(y*z + x);
}
VectReal_wp vx(hex.GetNbDof()), vy(hex.GetNbDof()), vz(hex.GetNbDof());
// we want to compute the integral against derivatives
(f_x against x-derivatives, f_y against y-derivatives, f_z against z-derivatives)
hex.ApplyRhSplit(feval, vx, vy, vz);
// ApplyRh actually computes res = vx + vy + vz
// example in 2-D : vz is not present
QuadrangleLobatto quad;
quad.ConstructFiniteElement(order);
feval.Reallocate(2*quad.GetNbPointsQuadratureInside());
feval.FillRand();
quad.ApplyRhSplit(feval, vx, vy);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ApplyRhQuadratureSplit
Syntax
| void ApplyRhQuadratureSplit(const Vector& feval, Vector& vx, Vector& vy) const |
This method is available only for scalar finite elements. It is similar to the method ApplyRhQuadrature, but the result is split into two vectors (three in 3-D). It computes the integral against the derivatives of basis functions (associated with quadrature points:
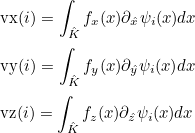
where f is a given function and ψi are basis functions associated with quadrature points. Since weights are included in input vector feval, the resulting vector is equal to

where xj are quadrature points. The method ApplyRhQuadrature is very close since the vectors vx, vy and vz are intricated in a single vector res.
Parameters
- feval (in)
- Evaluation of f on quadrature points of the face (multiplied by weights)
- vx (inout)
- integral against x-derivatives
- vy (inout)
- integral against y-derivatives
- vz (inout, 3D)
- integral against z-derivatives
Example :
HexahedronLobatto hex;
int order = 4;
hex.ConstructFiniteElement(order);
// we start from evaluation of f on quadrature points
VectReal_wp feval(3*hex.GetNbPointsQuadratureInside());
for (int i = 0; i < hex.GetNbPointsQuadratureInside(); i++)
{
R3 pt3D = hex.PointsND(i); Real_wp w = hex.WeightsND(i);
Real_wp x = pt3D(0), y = pt3D(1), z = pt3D(2);
feval(3*i) = w*exp(-x+y);
feval(3*i+1) = w*cos(x*z);
feval(3*i+2) = w*sin(y*z + x);
}
int N = hex.GetNbPointsQuadratureInside();
VectReal_wp vx(N), vy(N), vz(N);
// we want to compute the integral against derivatives
(f_x against x-derivatives, f_y against y-derivatives, f_z against z-derivatives)
hex.ApplyRhQuadratureSplit(feval, vx, vy, vz);
// example in 2-D : vz is not present
QuadrangleLobatto quad;
quad.ConstructFiniteElement(order);
feval.Reallocate(2*quad.GetNbPointsQuadratureInside());
feval.FillRand();
quad.ApplyRhQuadratureSplit(feval, vx, vy);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ApplyConstantRh
Syntax
| void ApplyConstantRh(const Vector& u, Vector& v) const |
This method computes v = R u where R is defined as
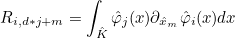
where φi are basis functions, d is the dimension. As a result, we have :
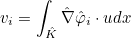
Therefore, it is similar to the method except that u is given in the finite element basis (instead of values on quadrature points multiplied by weights). The method ApplyConstantRh is available only for scalar finite elements. In the case where the jacobian matrix is uniform in the real element, the gradient matrix can be computed directly from this matrix R. The method ApplyConstantRh is usually used for affine elements that imply a constant jacobian. When the jacobian is not constant, the product with the gradient matrix on a real element is computed by calling ApplyChTranspose, multiply by the needed jacobian coefficients for each quadrature point, and call ApplyRh.
Example :
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
// computing integral of u against gradient of basis functions
// v_i = \int u \cdot \nabla \hat{\varphi}_i
VectReal_wp v(pyr.GetNbDof()), u(3*pyr.GetNbDof());
pyr.ApplyConstantRh(u, v);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ApplyConstantRhSplit
Syntax
| void ApplyConstantRhSplit(const Vector& u, Vector& vx, Vector& vy) const |
This method computes :
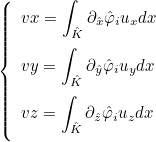
Therefore, it is similar to the method ApplyConstantRh except that v is split into vectors vx, vy, vz (v = vx + vy + vz). This method is available only for scalar elements
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // computing integral of u against derivatives of basis functions VectReal_wp vx(pyr.GetNbDof()), vy(pyr.GetNbDof()), vz(pyr.GetNbDof()), u(3*pyr.GetNbDof()); pyr.ApplyConstantRhSplit(u, vx, vy, vz);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ApplyConstantRhTranspose
Syntax
| void ApplyConstantRhTranspose(const Vector& u, Vector& v) const |
This method computes v = RT u where R is defined as
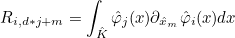
where φi are basis functions, d is the dimension. As a result, we have :
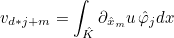
The method ApplyConstantRhTranspose is available only for scalar finite elements. In the case where the jacobian matrix is uniform in the real element, the gradient matrix can be computed directly from this matrix R. The method ApplyConstantRhTranspose is usually used for affine elements that imply a constant jacobian. When the jacobian is not constant, the transpose product with the gradient matrix on a real element is computed by calling ApplyRhTranspose, multiply by the needed jacobian coefficients for each quadrature point, and call ApplyCh.
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); VectReal_wp u(pyr.GetNbDof()), v(3*pyr.GetNbDof()); pyr.ApplyConstantRhTranspose(u, v);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
AddConstantMassMatrix
Syntax
| void AddConstantMassMatrix(int m, int n, Real_wp C, VirtualMatrix& A) const |
This method adds the mass matrix to the matrix A :
A[m:m+N, n:n+N] += M
where N is the number of degrees of freedom. The mass matrix M is given as
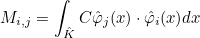
where C is a constant and φi are basis functions. C is a scalar for scalar finite elements, and a 2x2 matrix (3x3 in 3-D) for vectorial elements. This method is well suited to add a mass matrix when the transformation Fi is affine and when there is no variable physical index. For example if you have the following matrix in the real element Ke :
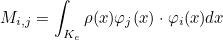
where ρ is a physical index. This integral is transformed in the reference element (for scalar elements):
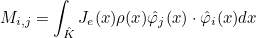
where Je is the determinant of the jacobian matrix DFe. Therefore, if the element is affine, this jacobian will be constant, and if ρ is also constant, you can set:
and call the method AddConstantMassMatrix. The destination matrix A derives from the class VirtualMatrix, it can be a symmetric or general matrix (even sparse).
Parameters
- m (in)
- starting row index for A
- n (in)
- starting column index for A
- C (in)
- coefficient (scalar for finite element, matrix for vectorial elements)
- A (inout)
- matrix to which the mass matrix will be added
Example :
PyramidClassical pyr; int order = 4; pyr.ConstructFiniteElement(order); // we want to compute only mass matrix int N = pyr.GetNbDof(); Real_wp jacob = 2.0, rho = 3.0; Real_wp C = jacob*rho; Matrix<Real_wp, Symmetric, RowSymPacked> M(N, N); M.Zero(); pyr.AddConstantMassMatrix(0, 0, C, M); // example with edge elements HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(order); N = hex.GetNbDof(); M.Reallocate(N, N); M.Zero(); // C is a tiny matrix (symmetric or not) 2x2 in 2-D and 3x3 in 3-D TinyMatrix<Real_wp, Symmetric, 3, 3> Cs; Cs.SetIdentity(); hex.AddConstantMassMatrix(0, 0, Cs, M);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
AddVariableMassMatrix
Syntax
| void AddVariableMassMatrix(int m, int n, VectReal_wp C, VirtualMatrix& A) const |
This method adds the mass matrix to the matrix A :
A[m:m+N, n:n+N] += M
where N is the number of degrees of freedom. The mass matrix M is given as
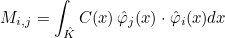
where C is a variable coefficient and φi are basis functions. C is a vector of scalars for scalar finite elements, and a vector of 2x2 matrices (3x3 in 3-D) for vectorial elements. This method is well suited to add a mass matrix when the transformation Fi is not affine or when there is a variable physical index. For example if you have the following matrix in the real element Ke :
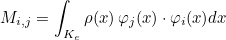
where ρ is a physical index. This integral is transformed in the reference element (for scalar elements):
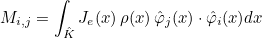
where Je is the determinant of the jacobian matrix DFe. Therefore, you can fill the vector C with :
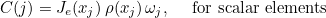
where xj, ωj are quadrature points and weights. Then you can call the method AddVariableMassMatrix. For vectorial elements, the expression is different due to Piola transform :
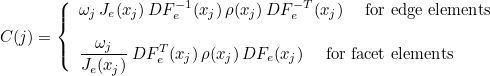
The destination matrix A derives from the class VirtualMatrix, it can be a symmetric or general matrix (even sparse). Since the weights are already included in C, the method performs the following operation:
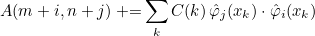
Parameters
- m (in)
- starting row index for A
- n (in)
- starting column index for A
- C (in)
- coefficient for each quadrature point (multiplied by the weight)
- A (inout)
- matrix to which the mass matrix will be added
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
pyr.SetMesh(mesh);
// computing jacobian matrices DF_e
int num_elem = 31; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> pts; SetMatrices<Dimension3> mat;
pyr.FjElemNodal(s, pts, mesh, num_elem);
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// we want to compute only mass matrix
int N = pyr.GetNbDof(); int Nquad = pyr.GetNbPointsQuadratureInside();
VectReal_wp C(Nquad);
// filling coefficient for each quadrature point (e.g. the jacobian)
// you have to multiply the coeffient by the weight
for (int i = 0; i < Nquad; i++)
C(i) = Det(mat.GetPointQuadrature(i))*pyr.WeightsND(i);
Matrix<Real_wp, Symmetric, RowSymPacked> M(N, N);
M.Zero();
pyr.AddVariableMassMatrix(0, 0, C, M);
// example with edge elements
PyramidHcurlFirstFamily pyr_edge;
pyr_edge.ConstructFiniteElement(order);
N = pyr_edge.GetNbDof();
M.Reallocate(N, N); M.Zero();
pyr_edge.FjElemNodal(s, pts, mesh, num_elem);
pyr_edge.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// taking into account Piola transform
Vector<Matrix3_3> Cs(Nquad); Matrix3_3 dfjm1;
for (int i = 0; i < Nquad; i++)
{
GetInverse(mat.GetPointQuadrature(i), dfjm1);
MltTrans(dfjm1, dfjm1, C(i));
C(i) *= Det(mat.GetPointQuadrature(i))*pyr_edge.WeightsND(i);
}
pyr_edge.AddVariableMassMatrix(0, 0, Cs, M);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
AddVariableElemMatrix
Syntax
| void AddVariableElemMatrix(int m, int n, VectReal_wp mass, VectMatrixN_N C, VectR_N D, VectR_N E, TinyVector<bool, 4> null_term, VirtualMatrix& A) const |
This method is available only for scalar finite elements. It adds an elementary matrix to the matrix A :
A[m:m+N, n:n+N] += B
where N is the number of degrees of freedom. The elementary matrix B is given as
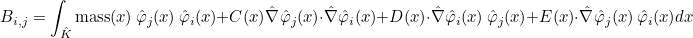
where mass, C, D and E are variable coefficients and φi are basis functions. mass is a vector of scalars, C is a vector of d x d matrices (d being the dimension), D and E are vectors of vectors of size d. For example if you have the following matrix in the real element Ke :
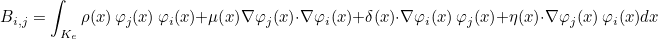
where ρ, μ, δ and η are physical indexes. This integral is transformed in the reference element :
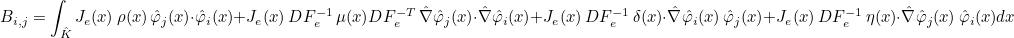
where Je is the determinant of the jacobian matrix DFe. Therefore, you can fill the vector mass, C, D and E with :
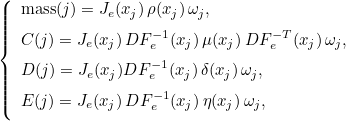
where xj, ωj are quadrature points and weights. Then you can call the method AddVariableElemMatrix. The destination matrix A derives from the class VirtualMatrix, it can be a symmetric or general matrix (even sparse). Since the weights are already included in the coefficients, the method performs the following operation:
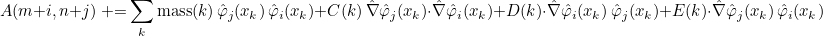
The argument null_term can be used if you want to skip some terms. If null_term(0) is true, the term with mass is not computed (nor added). If null_term(1) is true, the term with C is not computed. If null_term(2) (resp. null_term(3)) is true, the term with D (resp. E) is not computed.
Parameters
- m (in)
- starting row index for A
- n (in)
- starting column index for A
- mass (in)
- coefficient mass for each quadrature point (multiplied by the weight)
- C (in)
- coefficient C for each quadrature point (multiplied by the weight)
- D (in)
- coefficient D for each quadrature point (multiplied by the weight)
- E (in)
- coefficient E for each quadrature point (multiplied by the weight)
- null_term (in)
- if null_term(i) the i-th term is not computed
- A (inout)
- matrix to which the mass matrix will be added
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
pyr.SetMesh(mesh);
// computing jacobian matrices DF_e
int num_elem = 31; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> pts; SetMatrices<Dimension3> mat;
pyr.FjElemNodal(s, pts, mesh, num_elem);
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// we want to compute an elementary matrix
int N = pyr.GetNbDof(); int Nquad = pyr.GetNbPointsQuadratureInside();
VectReal_wp mass(Nquad); Vector<Matrix3_3> C(Nquad);
VectR3 D(Nquad), E(Nquad);
// using constant physical indexes (they can also vary)
Real_wp rho = 2.0; Matrix3_3 mu, tmp; mu.SetDiagonal(3.0);
R3 delta(0.8, 0.4, 0.2), eta(1.5, -0.2, 0.9);
// filling coefficient for each quadrature point
// you have to multiply the coeffients by the weight
for (int i = 0; i < Nquad; i++)
{
Real_wp jacob = Det(mat.GetPointQuadrature(i));
Matrix3_3 dfjm1; GetInverse(mat.GetPointQuadrature(i), dfjm1);
mass(i) = rho*jacob*pyr.WeightsND(i);
MltTrans(mu, dfjm1, tmp); Mlt(dfjm1, tmp, C(i));
C(i) *= jacob*pyr.WeightsND(i);
Mlt(dfjm1, delta, D(i));
D(i) *= jacob*pyr.WeightsND(i);
Mlt(dfjm1, eta, E(i));
E(i) *= jacob*pyr.WeightsND(i);
}
Matrix<Real_wp, Symmetric, RowSymPacked> A(N, N);
A.Zero();
TinyVector<bool, 4> null_term(false, false, false, false);
pyr.AddVariableElemMatrix(0, 0, mass, C, D, E, null_term, A);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
AddConstantElemMatrix
Syntax
| void AddConstantElemMatrix(int m, int n, Real_wp mass, MatrixN_N C, R_N D, R_N E, TinyVector<bool, 4> null_term, VirtualMatrix& A) const |
This method is available only for scalar finite elements. It adds an elementary matrix to the matrix A :
A[m:m+N, n:n+N] += B
where N is the number of degrees of freedom. The elementary matrix B is given as
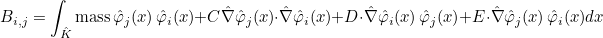
where mass, C, D and E are constant coefficients and φi are basis functions. mass is a scalar, C is a d x d matrix (d being the dimension), D and E are vectors of size d. For example if you have the following matrix in the real element Ke :
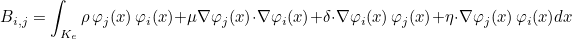
where ρ, μ, δ and η are constant physical indexes. This integral is transformed in the reference element :
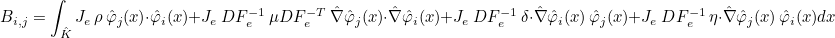
where Je is the determinant of the jacobian matrix DFe. If the element is affine, these quantities are constant. Therefore, you can set the coefficients mass, C, D and E with :
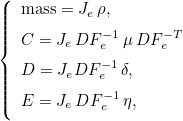
Then you can call the method AddConstantElemMatrix. The destination matrix A derives from the class VirtualMatrix, it can be a symmetric or general matrix (even sparse). The argument null_term can be used if you want to skip some terms. If null_term(0) is true, the term with mass is not computed (nor added). If null_term(1) is true, the term with C is not computed. If null_term(2) (resp. null_term(3)) is true, the term with D (resp. E) is not computed.
Parameters
- m (in)
- starting row index for A
- n (in)
- starting column index for A
- mass (in)
- coefficient mass
- C (in)
- coefficient C
- D (in)
- coefficient D
- E (in)
- coefficient E
- null_term (in)
- if null_term(i) the i-th term is not computed
- A (inout)
- matrix to which the mass matrix will be added
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
PyramidClassical pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
pyr.SetMesh(mesh);
// computing jacobian matrices DF_e
int num_elem = 31; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> pts; SetMatrices<Dimension3> mat;
pyr.FjElemNodal(s, pts, mesh, num_elem);
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// we want to compute an elementary matrix
int N = pyr.GetNbDof();
Real_wp mass; Matrix3_3 C; R3 D, E;
// using constant physical indexes (if they vary, use AddVariableElemMatrix)
Real_wp rho = 2.0; Matrix3_3 mu, tmp; mu.SetDiagonal(3.0);
R3 delta(0.8, 0.4, 0.2), eta(1.5, -0.2, 0.9);
// filling coefficient for each quadrature point
// you have to multiply the coeffients by the weight
Real_wp jacob = Det(mat.GetPointQuadrature(0));
Matrix3_3 dfjm1; GetInverse(mat.GetPointQuadrature(0), dfjm1);
mass = rho*jacob;
MltTrans(mu, dfjm1, tmp); Mlt(dfjm1, tmp, C);
C *= jacob;
Mlt(dfjm1, delta, D);
D *= jacob;
Mlt(dfjm1, eta, E);
E *= jacob;
Matrix<Real_wp, Symmetric, RowSymPacked> A(N, N);
A.Zero();
TinyVector<bool, 4> null_term(false, false, false, false);
pyr.AddConstantElemMatrix(0, 0, mass, C, D, E, null_term, A);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
AddConstantStiffnessMatrix
Syntax
| void AddConstantStiffnessMatrix(int m, int n, Real_wp C, VirtualMatrix& A) const |
This method is available for vectorial elements. For scalar finite elements, the user can call AddConstantElemMatrix. This method adds the stiffness matrix to the matrix A :
A[m:m+N, n:n+N] += K
where N is the number of degrees of freedom. The stiffness matrix K is given as
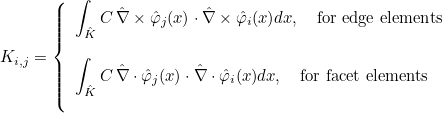
where C is a constant and φi are basis functions. C is a scalar for 2-D edge elements or facet elements, and a 3x3 matrix for 3-D edge elements. This method is well suited to add a stiffness matrix when the transformation Fi is affine and when there is no variable physical index. For example if you have the following matrix in the real element Ke (for 3-D edge elements) :
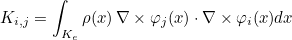
where ρ is a physical index. This integral is transformed in the reference element :
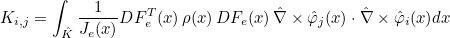
where Je is the determinant of the jacobian matrix DFe. Therefore, if the element is affine, this jacobian will be constant, and if ρ is also constant, you can set:
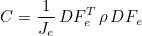
and call the method AddConstantStiffnessMatrix. For facet elements, the stiffness matrix on the real element :
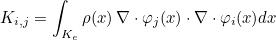
is transformed in the reference element :
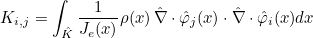
For facet elements, the constant C is equal to
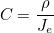
The destination matrix A derives from the class VirtualMatrix, it can be a symmetric or general matrix (even sparse).
Parameters
- m (in)
- starting row index for A
- n (in)
- starting column index for A
- C (in)
- coefficient
- A (inout)
- matrix to which the stiffness matrix will be added
Example :
PyramidHdivFirstFamily pyr; int order = 4; pyr.ConstructFiniteElement(order); // we want to compute only stifness matrix int N = pyr.GetNbDof(); Real_wp jacob = 2.0, rho = 3.0; Real_wp C = rho/jacob; Matrix<Real_wp, Symmetric, RowSymPacked> K(N, N); K.Zero(); pyr.AddConstantStifnessMatrix(0, 0, C, K); // example with 3-D edge elements HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(order); N = hex.GetNbDof(); K.Reallocate(N, N); K.Zero(); // C is a 3x3 tiny matrix (symmetric or not) TinyMatrix<Real_wp, Symmetric, 3, 3> Cs; Cs.SetIdentity(); hex.AddConstantStiffnessMatrix(0, 0, Cs, K);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
AddVariableStiffnessMatrix
Syntax
| void AddVariableStiffnessMatrix(int m, int n, VectReal_wp C, VirtualMatrix& A) const |
This method is available for vectorial elements. For scalar finite elements, the user can call AddVariableElemMatrix. This method adds the stiffness matrix to the matrix A :
A[m:m+N, n:n+N] += K
where N is the number of degrees of freedom. The stiffness matrix K is given as
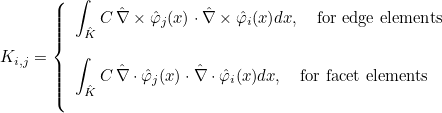
where C is a variable coefficient and φi are basis functions. C is a vector of scalars for 2-D edge elements or facet elements, and a vector of 3x3 matrices for 3-D edge elements. This method is well suited to add a stiffness matrix when the transformation Fi is not affine or when there is a variable physical index. For example if you have the following matrix in the real element Ke (for 3-D edge elements):
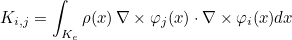
where ρ is a physical index. This integral is transformed in the reference element :
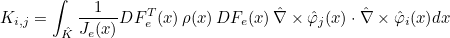
where Je is the determinant of the jacobian matrix DFe. Therefore, you can fill the vector C with :
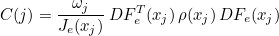
where xj, ωj are quadrature points and weights. Then you can call the method AddVariableStiffnessMatrix. For facet elements, the stiffness matrix on the real element :
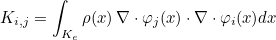
is transformed in the reference element :
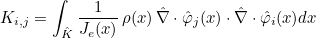
For facet elements, the vector C is equal to
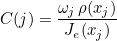
The destination matrix A derives from the class VirtualMatrix, it can be a symmetric or general matrix (even sparse). Since the weights are already included in C, the method performs the following operation:
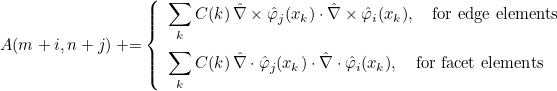
Parameters
- m (in)
- starting row index for A
- n (in)
- starting column index for A
- C (in)
- coefficient for each quadrature point (multiplied by the weight)
- A (inout)
- matrix to which the stiffness matrix will be added
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
PyramidHdivFirstFamily pyr;
int order = 4;
pyr.ConstructFiniteElement(order);
pyr.SetMesh(mesh);
// computing jacobian matrices DF_e
int num_elem = 31; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> pts; SetMatrices<Dimension3> mat;
pyr.FjElemNodal(s, pts, mesh, num_elem);
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// we want to compute only stiffness matrix
int N = pyr.GetNbDof(); int Nquad = pyr.GetNbPointsQuadratureInside();
VectReal_wp C(Nquad);
// filling coefficient for each quadrature point (e.g. the jacobian)
// you have to multiply the coeffient by the weight
for (int i = 0; i < Nquad; i++)
C(i) = pyr.WeightsND(i) / Det(mat.GetPointQuadrature(i));
Matrix<Real_wp, Symmetric, RowSymPacked> K(N, N);
K.Zero();
pyr.AddVariableMassMatrix(0, 0, C, K);
// example with edge elements
PyramidHcurlFirstFamily pyr_edge;
pyr_edge.ConstructFiniteElement(order);
N = pyr_edge.GetNbDof();
K.Reallocate(N, N); K.Zero();
pyr_edge.FjElemNodal(s, pts, mesh, num_elem);
pyr_edge.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// taking into account Piola transform
Vector<Matrix3_3> Cs(Nquad); Matrix3_3 dfj_trans;
for (int i = 0; i < Nquad; i++)
{
Transpose(mat.GetPointQuadrature(i), dfj_trans);
MltTrans(dfj_trans, dfj_trans, C(i));
C(i) *= pyr_edge.WeightsND(i) / Det(mat.GetPointQuadrature(i));
}
pyr_edge.AddVariableStiffnessMatrix(0, 0, Cs, K);
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
FindH1RotationTri
Syntax
| static void FindH1RotationTri(int r, const VectR2& Points2D, const VectReal_wp& Weights2D, const Matrix<Real_wp>& ValuePhi, NumberMap& nmap) |
This method is available only for 2-D scalar finite elements. It computes how degrees of freedom located on a triangular face are transformed when a rotation is applied to the face. It modifies the output argument nmap with the computed informations. This method is called in ConstructNumberMap of 3-D finite element classes.
Parameters
- r (in)
- order of approximation
- Points2D (in)
- quadrature points on the unit triangle
- Weights2D (in)
- quadrature weights on the unit triangle
- ValuePhi (in)
- values of 2-D basis functions on quadrature points
- nmap (inout)
- object storing informations about numbering
Example :
class MyTetra : public TetrahedronReference<1>
{
public:
void ConstructNumberMap(NumberMap& nmap, int dg_form)
{
// constructing ValuePhi : trace of 3-D basis functions on a
triangular face
int Nquad = this->Points2D_tri().GetM();
int nb_dof = this->GetNbDofBoundary(0);
Matrix<Real_wp> ValuePhi(nb_dof, Nquad);
for (int j = 0; j < Nquad; j++)
{
R3 pt; this->GetLocalCoordOnBoundary(0, this->Points2D_tri()(j), pt);
VectReal_wp phi; this->ComputeValuesPhiRef(pt, phi);
for (int i = 0; i < nb_dof; i++)
ValuePhi(i, j) = phi(i);
}
// constructing the numbers after a rotation of a triangular face
// (or linear operators if dofs are not invariant by rotation)
ElementReference<Dimension2, 1>::FindH1RotationTri(this->order, this->Points2D_tri(), this->Weights2D_tri(), ValuePhi, nmap);
}
};
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FindHdivRotationTri
Syntax
| static void FindHdivRotationTri(int r, const VectR2& Points2D, const VectReal_wp& Weights2D, const Matrix<Real_wp>& ValuePhi, NumberMap& nmap) |
This method is available only for 2-D facet finite elements. It computes how degrees of freedom located on a triangular face are transformed when a rotation is applied to the face. It modifies the output argument nmap with the computed informations. This method is called in ConstructNumberMap of 3-D facet element classes.
Parameters
- r (in)
- order of approximation
- Points2D (in)
- quadrature points on the unit triangle
- Weights2D (in)
- quadrature weights on the unit triangle
- ValuePhi (in)
- values of 2-D basis functions on quadrature points
- nmap (inout)
- object storing informations about numbering
Example :
class MyTetra : public TetrahedronReference<1>
{
public:
void ConstructNumberMap(NumberMap& nmap, int dg_form)
{
// constructing ValuePhi : trace of 3-D basis functions on a
triangular face
int Nquad = this->Points2D_tri().GetM();
int nb_dof = this->GetNbDofBoundary(0);
Matrix<Real_wp> ValuePhi(nb_dof, Nquad);
for (int j = 0; j < Nquad; j++)
{
R3 pt; this->GetLocalCoordOnBoundary(0, this->Points2D_tri()(j), pt);
VectR3 phi; this->ComputeValuesPhiRef(pt, phi);
for (int i = 0; i < nb_dof; i++)
ValuePhi(i, j) = DotProd(phi(i), this->NormaleLoc(0));
}
// constructing the numbers after a rotation of a triangular face
// (or linear operators if dofs are not invariant by rotation)
ElementReference<Dimension2, 3>::FindHdivRotationTri(this->order, this->Points2D_tri(), this->Weights2D_tri(), ValuePhi, nmap);
}
};
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FindHdivRotationQuad
Syntax
| static void FindHdivRotationQuad(int r, const VectR2& Points2D, const VectReal_wp& Weights2D, const Matrix<Real_wp>& ValuePhi, NumberMap& nmap) |
This method is available only for 2-D facet finite elements. It computes how degrees of freedom located on a quadrangular face are transformed when a rotation is applied to the face. It modifies the output argument nmap with the computed informations. This method is called in ConstructNumberMap of 3-D facet element classes.
Parameters
- r (in)
- order of approximation
- Points2D (in)
- quadrature points on the unit square
- Weights2D (in)
- quadrature weights on the unit square
- ValuePhi (in)
- values of 2-D basis functions on quadrature points
- nmap (inout)
- object storing informations about numbering
Example :
class MyHexa : public HexahedronReference<1>
{
public:
void ConstructNumberMap(NumberMap& nmap, int dg_form)
{
// constructing ValuePhi : trace of 3-D basis functions on a
quadrangular face
int Nquad = this->Points2D_quad().GetM();
int nb_dof = this->GetNbDofBoundary(0);
Matrix<Real_wp> ValuePhi(nb_dof, Nquad);
for (int j = 0; j < Nquad; j++)
{
R3 pt; this->GetLocalCoordOnBoundary(0, this->Points2D_tri()(j), pt);
VectR3 phi; this->ComputeValuesPhiRef(pt, phi);
for (int i = 0; i < nb_dof; i++)
ValuePhi(i, j) = DotProd(phi(i), this->NormaleLoc(0));
}
// constructing the numbers after a rotation of a triangular face
// (or linear operators if dofs are not invariant by rotation)
ElementReference<Dimension2, 3>::FindHdivRotationQuad(this->order, this->Points2D_quad(), this->Weights2D_quad(), ValuePhi, nmap);
}
};
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FindHcurlRotationTri
Syntax
| void FindHcurlRotationTri( NumberMap& nmap, int offset) const |
This method is available only for 2-D edge elements. It computes how degrees of freedom located on a triangular face are transformed when a rotation is applied to the face. It modifies the output argument nmap with the computed informations. This method is called in ConstructNumberMap of 3-D edge element classes. The last argument is used to select (or not) only interior dofs of the face.
Parameters
- nmap (inout)
- object storing informations about numbering
- offset (in)
- dofs with number ≥ offset are considered
Example :
class MyTetra : public TetrahedronReference<2>
{
public:
void ConstructNumberMap(NumberMap& nmap, int dg_form)
{
// we use the 2-D surface finite element
element_tri_surf->FindHcurlRotationTri(nmap, this->GetNbDofBoundaries());
}
};
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
FindHcurlRotationQuad
Syntax
| void FindHcurlRotationQuad( NumberMap& nmap, int offset) |
This method is available only for 2-D edges elements. It computes how degrees of freedom located on a quadrangular face are transformed when a rotation is applied to the face. It modifies the output argument nmap with the computed informations. This method is called in ConstructNumberMap of 3-D edge element classes. The last argument is used to select (or not) only interior dofs of the face.
Parameters
- nmap (inout)
- object storing informations about numbering
- offset (in)
- dofs with number ≥ offset are considered
Example :
class MyHexa : public HexahedronReference<2>
{
public:
void ConstructNumberMap(NumberMap& nmap, int dg_form)
{
// we use the 2-D surface finite element
element_quad_surf->FindHcurlRotationQuad(nmap, this->GetNbDofBoundaries());
}
};
Location :
FiniteElement/FaceReference.hxx
FiniteElement/FaceReference.cxx
ComputeTriangularInterpolationProjectorOrder
Syntax
| void ComputeTriangularInterpolationProjectorOrder( const IVect& list_order, Vector<VectR2>& pts_quad) |
This method is present for 3-D finite elements. You can provide manually a list of orders with the associated quadrature points. The interpolators are constructed for triangular faces such that ApplySh and ApplyShTranspose can be called with a order of the list. This construction is done automatically by the method (orders are collected by looking at neighboring elements).
Parameters
- list_order (in)
- list of orders
- pts_quad (in)
- quadrature points for each order
Example :
TetrahedronClassical tet; tet.ConstructFiniteElement(4); // computing interpolation for order 3 and 5 IVect order(2); order(0) = 3; order(1) = 5; Vector<VectR2> pts(2); VectReal_wp weights; TriangleQuadrature::ConstructQuadrature(2*order(0), pts(0), weights); TriangleQuadrature::ConstructQuadrature(2*order(1), pts(1), weights); tet.ComputeTriangularInterpolationProjectorOrder(order, pts);
Location :
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeQuadrangularInterpolationProjectorOrder
Syntax
| void ComputeQuadrangularInterpolationProjectorOrder( const IVect& list_order, Vector<VectR2>& pts_quad) |
This method is present for 3-D finite elements. You can provide manually a list of orders with the associated quadrature points. The interpolators are constructed for quadrangular faces such that ApplySh and ApplyShTranspose can be called with a order of the list. This construction is done automatically by the method (orders are collected by looking at neighboring elements).
Parameters
- list_order (in)
- list of orders
- pts_quad (in)
- quadrature points for each order
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(4); // computing interpolation for order 3 and 5 IVect order(2); order(0) = 3; order(1) = 5; Vector<VectR2> pts(2); VectReal_wp weights; QuadrangleQuadrature::ConstructQuadrature(2*order(0), pts(0), weights); QuadrangleQuadrature::ConstructQuadrature(2*order(1), pts(1), weights); hex.ComputeQuadrangularInterpolationProjectorOrder(order, pts);
Location :
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
GetTriangularSurfaceFiniteElement
Syntax
| const ElementReference& GetTriangularSurfaceFiniteElement() const |
This method returns the 2-D finite element for triangles. It is the trace of the 3-D finite element on triangular faces.
Example :
TetrahedronClassical tet; tet.ConstructFiniteElement(4); // if you need the 2-D finite element (trace on triangular faces) const ElementReference<Dimension2, 1>& tri = tet.GetTriangularSurfaceFiniteElement(); // example with edge elements WedgeHcurlFirstFamily wed; wed.ConstructFiniteElement(4); const ElementReference<Dimension2, 2>& tri_edge = wed.GetTriangularSurfaceFiniteElement();
Location :
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
GetQuadrangularSurfaceFiniteElement
Syntax
| const ElementReference& GetQuadrangularSurfaceFiniteElement() const |
This method returns the 2-D finite element for quadrilaterals. It is the trace of the 3-D finite element on quadrangular faces.
Example :
HexahedronGauss hex; hex.ConstructFiniteElement(4); // if you need the 2-D finite element (trace on quadrangular faces) const ElementReference<Dimension2, 1>& quad = hex.GetQuadrangularSurfaceFiniteElement(); // example with edge elements WedgeHcurlFirstFamily wed; wed.ConstructFiniteElement(4); const ElementReference<Dimension2, 2>& quad_edge = wed.GetQuadrangularSurfaceFiniteElement();
Location :
FiniteElement/VolumeReference.hxx
FiniteElement/VolumeReference.cxx
ComputeValuesPhi
Syntax
| void ComputeValuesPhi(const R_N& pt_loc, Vector& phi, const Matrix& dfjm1, const MeshNumbering& mesh_num, int num_elem) const |
This method computes the basis functions on the real element. They are linked with basis functions on the reference element with the following relations :
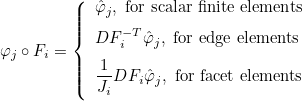
where Ji is the determinant of jacobian matrix DFi. This method also takes into account the effect of face orientations (if there are signs or linear operators to compute global degrees of freedom from local degrees of freedom), such that the values of global basis functions is given.
Parameters
- pt_loc (in)
- local point on the reference element
- phi (out)
- global basis functions evaluated at pt_loc
- dfjm1 (in)
- matrix DFi-1(pt_loc)
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); hex.FjElemNodal(s, pts, mesh, num_elem); // if you want to compute phi_i for a given point R3 pt_loc(0.4, 0.1, 0.2); // point on the reference element // compute the jacobian matrix dfj = DFi(pt_loc) and its inverse Matrix3_3 dfj, dfjm1; hex.DFj(s, pts, pt_loc, dfj, mesh, num_elem); GetInverse(dfj, dfjm1); // then you can evaluate the basis functions (one component for scalar elements) Vector<TinyVector<Real_wp, 1> > phi; pyr.ComputeValuesPhi(pt_loc, phi, dfjm1, mesh_num, num_elem); // example with edge elements : HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // then you can evaluate the basis functions VectR3 phi_hex; hex.ComputeValuesPhi(pt_loc, phi_hex, dfjm1, mesh_num, num_elem); VectReal_wp u(mesh_num.GetNbDof()); u.FillRand(); // they can be used directly to compute the solution on the chosen point // (signs and rotation of dofs are already treated in ComputeValuesPhi) R3 u_pt = 0; for (int i = 0; i < phi_hex.GetM(); i++) u_pt += u(mesh_num.Element(num_elem).GetNumberDof(i)) * phi_hex(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeValuesGradientPhi
Syntax
| void ComputeValuesPhi(const R_N& pt_loc, Vector& nabla_phi, const Matrix& dfjm1, const MeshNumbering& mesh_num, int num_elem) const |
This method computes the gradient of basis functions on the real element. For edge elements, the curl is computed, whereas the divergence is computed for facet elements. These quantities are linked with the basis functions on the reference element with the following relations :
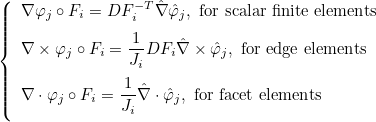
where Ji is the determinant of jacobian matrix DFi. This method also takes into account the effect of face orientations (if there are signs or linear operators to compute global degrees of freedom from local degrees of freedom), such that the gradient (or curl/div) of global basis functions is given.
Parameters
- pt_loc (in)
- local point on the reference element
- nabla_phi (out)
- gradient (curl for edge elements, divergence for facet element) of global basis functions evaluated at pt_loc
- dfjm1 (in)
- matrix DFi-1(pt_loc)
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); hex.FjElemNodal(s, pts, mesh, num_elem); // if you want to compute phi_i for a given point R3 pt_loc(0.4, 0.1, 0.2); // point on the reference element // compute the jacobian matrix dfj = DFi(pt_loc) and its inverse Matrix3_3 dfj, dfjm1; hex.DFj(s, pts, pt_loc, dfj, mesh, num_elem); GetInverse(dfj, dfjm1); // then you can evaluate the gradient of basis functions VectR3 grad_phi; pyr.ComputeValuesGradientPhi(pt_loc, grad_phi, dfjm1, mesh_num, num_elem); // example with edge elements : HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // then you can evaluate the curl of basis functions VectR3 curl_phi; hex.ComputeValuesGradientPhi(pt_loc, curl_phi, dfjm1, mesh_num, num_elem); VectReal_wp u(mesh_num.GetNbDof()); u.FillRand(); // they can be used directly to compute the curl of solution on the chosen point // (signs and rotation of dofs are already treated in ComputeValuesGradientPhi) R3 curl_u_pt = 0; for (int i = 0; i < curl_phi.GetM(); i++) curl_u_pt += u(mesh_num.Element(num_elem).GetNumberDof(i)) * curl_phi(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
GetCurlFromGradient
Syntax
| static void GetCurlFromGradient(const Vector<Vector>& grad_u, Vector<Vector>& curl_u) |
This method allows to compute the curl of a field from gradients for edge elements. For facet elements, this method will compute the divergence of the field. For scalar finite elements, this method equals curl_u to grad_u.
Parameters
- grad_u (in)
- gradient of components of the field
- curl_u (out)
- curl of the field
Example :
// in 3-D, we consider a field E with three components Ex, Ey, and Ez // three gradients per components => nine values in total // if you have several unknowns, you can allocate grad_E with 9*nb_unknowns // and the curl will be computed for all the unknowns Vector<VectReal_wp> grad_E(9); // for each value, we allocate with the number of points (the curl is computed for each point) int nb_pts = 20; for (int i = 0; i < 9; i++) grad_E(i).Reallocate(nb_pts); // filling the gradient of Ex for the first point : int num_pt = 0; grad_E(0)(num_pt) = 0.2; grad_E(1)(num_pt) = 0.5; grad_E(2)(num_pt) = 0.8; // grad(Ex) = (0.2, 0.5, 0.8) for this point // gradient of Ey grad_E(3)(num_pt) = 0.9; grad_E(4)(num_pt) = 0.3; grad_E(5)(num_pt) = 1.7; // gradient of Ez grad_E(6)(num_pt) = -0.5; grad_E(7)(num_pt) = -2.1; grad_E(8)(num_pt) = 0.1; // then you can fill gradient for the next point num_pt++; grad_E(0)(num_pt) = 0.4; grad_E(1)(num_pt) = 2.7; grad_E(2)(num_pt) = 2.6; grad_E(3)(num_pt) = 2.2; grad_E(4)(num_pt) = -1.3; grad_E(5)(num_pt) = -3.2; grad_E(6)(num_pt) = -3.1; grad_E(7)(num_pt) = 1.8; grad_E(8)(num_pt) = 1.9; // etc // then you compute the curl for all points Vector<VectReal_wp> curl_E; FiniteElementHcurl<Dimension3>::GetCurlFromGradient(grad_E, curl_E); // curl on the first point num_pt = 0; R3 curl1(curl_E(0)(num_pt), curl_E(1)(num_pt), curl_E(2)(num_pt)); // on the next point num_pt++; R3 curl2(curl_E(0)(num_pt), curl_E(1)(num_pt), curl_E(2)(num_pt)); // etc // for facet elements, we compute the divergence Vector<VectReal_wp> div_E; FiniteElementHdiv<Dimension3>::GetCurlFromGradient(grad_E, div_E); // divergence on the first point num_pt = 0; Real_wp div1 = div_E(0)(num_pt); // on the next point num_pt++; Real_wp div2 = div_E(0)(num_pt); // etc
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeValuesPhiBoundary
Syntax
| void ComputeValuesPhiBoundary( | Matrix<R3>& val_phi, const SetMatrices& MatricesElem, |
| const MeshNumbering& mesh_num, int num_elem, int num_loc) const |
This method computes the basis functions on the real element for quadrature points on the given boundary. They are linked with basis functions on the reference element with the following relations :
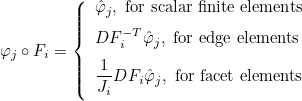
where Ji is the determinant of jacobian matrix DFi. This method also takes into account the effect of face orientations (if there are signs or linear operators to compute global degrees of freedom from local degrees of freedom), such that the values of global basis functions is given. The values of basis functions are stored in a matrix with the following convention
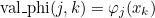
where xk is the k-th quadrature point of the face (edge in 2-D) num_loc of the element num_elem.
Parameters
- val_phi (out)
- global basis functions evaluated at quadrature points of the face (edge in 2-D)
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
- num_loc (in)
- local face number (edge number in 2-D)
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for quadrature points SetMatrices<Dimension3> mat; pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // and for the face int num_loc = 1; pyr.FjSurfaceElem(s, pts, mesh, num_elem, num_loc); pyr.DFjSurfaceElem(s, pts, mat, mesh, num_elem, num_loc); // then you can evaluate the basis functions on quadrature points of the face Matrix<TinyVector<Real_wp, 1> > phi; // one component for scalar elements pyr.ComputeValuesPhiBoundary(phi, mat, mesh_num, num_elem, num_loc); // phi on first quadrature point : int j = 3, num_pt = 0; Real_wp phi_j = phi(j, num_pt); // here j is the local dof number on the element, and not on the boundary // because for some elements, all basis functions may contribute to the boundary // example with edge elements : HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // then you can evaluate the basis functions on quadrature points of the face Matrix<R3> phi_hex; hex.ComputeValuesPhiBoundary(phi_hex, mat, mesh_num, num_elem, num_loc);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeValuesGradientPhiBoundary
Syntax
| void ComputeValuesGradientPhiBoundary( | Matrix<R3>& nabla_phi, const SetMatrices& MatricesElem, |
| const MeshNumbering& mesh_num, int num_elem, int num_loc) const |
This method computes the gradient of basis functions on the real element for quadrature points on the given boundary. For edge elements, the curl is computed, whereas the divergence is computed for facet elements. These quantities are linked with basis functions on the reference element with the following relations :
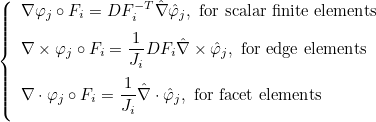
where Ji is the determinant of jacobian matrix DFi. This method also takes into account the effect of face orientations (if there are signs or linear operators to compute global degrees of freedom from local degrees of freedom), such that the gradient (or curl/div) of global basis functions is given. The gradient of basis functions are stored in a matrix with the following convention
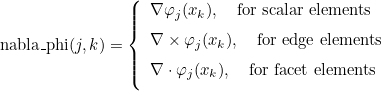
where xk is the k-th quadrature point of the face (edge in 2-D) num_loc of the element num_elem.
Parameters
- nabla_phi (out)
- gradient (curl for edge elements, divergence for facet element) of global basis functions evaluated at quadrature points of the face (edge in 2-D)
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
- num_loc (in)
- local face number (edge number in 2-D)
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for quadrature points SetMatrices<Dimension3> mat; pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // and for the face int num_loc = 1; pyr.FjSurfaceElem(s, pts, mesh, num_elem, num_loc); pyr.DFjSurfaceElem(s, pts, mat, mesh, num_elem, num_loc); // then you can evaluate the gradient of basis functions on quadrature points of the face Matrix<R3> grad_phi; pyr.ComputeValuesGradientPhiBoundary(grad_phi, mat, mesh_num, num_elem, num_loc); // grad(phi) on first quadrature point : int j = 3, num_pt = 0; R3 grad_phi_j = grad_phi(j, num_pt); // here j is the local dof number on the element, and not on the boundary // because for some elements, all basis functions may contribute to the boundary // example with edge elements : HexahedronHcurlFirstFamily hex; hex.ConstructFiniteElement(3); // then you can evaluate the curl of basis functions on quadrature points of the face Matrix<R3> curl_phi_hex; hex.ComputeValuesGradientPhiBoundary(curl_phi_hex, mat, mesh_num, num_elem, num_loc);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeNodalValues
Syntax
| void ComputeNodalValues( | const SetMatrices& MatricesElem, const Vector<Vector>& Uloc, Vector<Vector>& Unodal, |
| const Mesh& mesh, int num_elem) const |
This method computes the nodal values of a field (in the real space) from components of this field on degrees of freedom of the element num_elem. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in Uloc(m) where m is the unknown number.
Parameters
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- Uloc (in)
- components of the field on degrees of freedom of the element
- Unodal (in)
- values of the field on nodal points of the element
- mesh (in)
- considered mesh
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // global solution on all the mesh int nb_unknowns = 2; VectReal_wp u_glob(mesh_num.GetNbDof()*nb_unknowns); u_glob.FillRand(); // extracting the local components of the solution on the selected element int num_elem = 40; Vector<VectReal_wp> u_loc(nb_unknowns); mesh_num.number_map.GetLocalUnknownVector(mesh_num, u_glob, num_elem, u_loc); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for nodal points SetMatrices<Dimension3> mat; pyr.DFjElemNodal(s, pts, mat, mesh, num_elem); // computation of the solution on nodal points of the element Vector<VectReal_wp> u_nodal; pyr.ComputeNodalValues(mat, u_loc, u_nodal, mesh, num_elem); // value on a node int num_unknown = 0, num_pt = 4; Real_wp u = u_nodal(num_unknown)(num_pt);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeQuadratureValues
Syntax
| void ComputeQuadratureValues( | const SetMatrices& MatricesElem, const Vector<Vector>& Uloc, Vector<Vector>& Uquad, |
| const Mesh& mesh, int num_elem) const |
This method computes the values of a field (in the real space) on quadrature points from components of this field on degrees of freedom of the element num_elem. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in Uloc(m) where m is the unknown number.
Parameters
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- Uloc (in)
- components of the field on degrees of freedom of the element
- Uquad (in)
- values of the field on quadrature points of the element
- mesh (in)
- considered mesh
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // global solution on all the mesh int nb_unknowns = 2; VectReal_wp u_glob(mesh_num.GetNbDof()*nb_unknowns); u_glob.FillRand(); // extracting the local components of the solution on the selected element int num_elem = 40; Vector<VectReal_wp> u_loc(nb_unknowns); mesh_num.number_map.GetLocalUnknownVector(mesh_num, u_glob, num_elem, u_loc); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for quadrature points SetMatrices<Dimension3> mat; pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // computation of the solution on quadrature points of the element Vector<VectReal_wp> u_quad; pyr.ComputeQuadratureValues(mat, u_loc, u_quad, mesh, num_elem); // value on a point int num_unknown = 0, num_pt = 4; Real_wp u = u_quad(num_unknown)(num_pt);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeProjectionDof
Syntax
| void ComputeProjectionDof( | const SetMatrices& MatricesElem, Vector<Vector>& feval, Vector<Vector>& f_proj, |
| const MeshNumbering& mesh_num, int num_elem) const |
This method projects a function (in real space) on degrees of freedom of the element num_elem. The input array feval contains the evaluation of the function on dof points. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in feval(m) where m is the unknown number. The projection is performed on global basis functions, such that the result can be directly inserted in the global solution.
Parameters
- MatricesElem (in)
- object storing matrices DFi at dof points
- feval (inout)
- values of the field to project on dof points
- f_proj (out)
- components of the field on degrees of freedom
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh;
MeshNumbering<Dimension3> mesh_num(mesh);
PyramidClassical pyr;
pyr.ConstructFiniteElement(3);
pyr.SetMesh(mesh);
// global projected field on the mesh
VectReal_wp f_glob(mesh_num.GetNbDof());
int num_elem = 15;
// computing transformation Fi for dof points
SetPoints<Dimension3> pts; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
pyr.FjElemDof(s, pts, mesh, num_elem);
// computing jacobian matrices DFi for dof points
SetMatrices<Dimension3> mat;
pyr.DFjElemDof(s, pts, mat, mesh, num_elem);
// evaluation of the functions to be projected
// f0 = sin(x+y*z), f1 = cos(x*y - z)
// these functions must be evaluated on dof points
int nb_unknowns = 2;
Vector<VectReal_wp> f_eval(nb_unknowns), f_proj;
f_eval(0).Reallocate(pyr.GetNbPointsDof()); f_eval(1).Reallocate(pyr.GetNbPointsDof());
for (int i = 0; i < pyr.GetNbPointsDof(); i++)
{
Real_wp x = pts.GetPointDof(i)(0), y = pts.GetPointDof(i)(1), z = pts.GetPointDof(i)(2);
f_eval(0)(i) = sin(x + y*z); f_eval(1)(i) = cos(x*y - z);
}
// projection on the element
pyr.ComputeProjectionDof(mat, f_eval, f_proj, mesh_num, num_elem);
// then you can insert the values on the global vector (here we insert only first unknown)
for (int i = 0; i < pyr.GetNbDof(); i++)
f_glob(mesh_num.Element(num_elem).GetNumberDof(i)) = f_proj(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeProjectionSurfaceDof
Syntax
| void ComputeProjectionSurfaceDof( | const SetMatrices& MatricesElem, Vector<Vector>& feval, Vector<Vector>& f_proj, |
| const MeshNumbering& mesh_num, int num_elem, int num_loc) const |
This method projects a function (in real space) on degrees of freedom of the face num_loc of the element num_elem. The input array feval contains the evaluation of the function on dof points of the face. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in feval(m) where m is the unknown number. The projection is performed on global basis functions, such that the result can be directly inserted in the global solution.
Parameters
- MatricesElem (in)
- object storing matrices DFi at dof points
- feval (inout)
- values of the field to project on dof points of the face
- f_proj (out)
- components of the field on degrees of freedom of the face
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
- num_loc (in)
- local face number (edge number in 2-D)
Example :
Mesh<Dimension3> mesh;
MeshNumbering<Dimension3> mesh_num(mesh);
PyramidClassical pyr;
pyr.ConstructFiniteElement(3);
pyr.SetMesh(mesh);
// global projected field on the mesh
VectReal_wp f_glob(mesh_num.GetNbDof());
int num_elem = 15;
// computing transformation Fi for dof points
SetPoints<Dimension3> pts; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
pyr.FjElemDof(s, pts, mesh, num_elem);
// computing jacobian matrices DFi for dof points
SetMatrices<Dimension3> mat;
pyr.DFjElemDof(s, pts, mat, mesh, num_elem);
// points of the face
int num_loc = 1;
pyr.FjSurfaceElemDof(s, pts, mesh, num_elem, num_loc);
pyr.DFjSurfaceElemDof(s, pts, mat, mesh, num_elem, num_loc);
// evaluation of the functions to be projected
// f0 = sin(x+y*z), f1 = cos(x*y - z)
// these functions must be evaluated on dof points of the boundary
int nb_unknowns = 2;
Vector<VectReal_wp> f_eval(nb_unknowns), f_proj;
int N = pyr.GetNbPointsDofSurface(num_loc);
f_eval(0).Reallocate(N); f_eval(1).Reallocate(N);
for (int i = 0; i < N; i++)
{
Real_wp x = pts.GetPointDofBoundary(i)(0), y = pts.GetPointDofBoundary(i)(1), z = pts.GetPointDofBoundary(i)(2);
f_eval(0)(i) = sin(x + y*z); f_eval(1)(i) = cos(x*y - z);
}
// projection on the face of the element
pyr.ComputeProjectionSurfaceDof(mat, f_eval, f_proj, mesh_num, num_elem, num_loc);
// then you can insert the values on the global vector (here we insert only first unknown)
for (int i = 0; i < pyr.GetNbDofBoundary(num_loc); i++)
{
int j = pyr.GetLocalNumber(num_loc, i);
f_glob(mesh_num.Element(num_elem).GetNumberDof(j)) = f_proj(i);
}
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeIntegral
Syntax
| void ComputeIntegral( | const SetMatrices& MatricesElem, Vector<Vector>& feval, Vector<Vector>& res, |
| const MeshNumbering& mesh_num, int num_elem) const |
This method computes the integral of a function over the real element Ke against basis functions of the element num_elem:
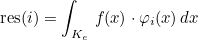
The input array feval contains the evaluation of the function on quadrature points. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in feval(m) where m is the unknown number. The integral is performed with global basis functions, such that the result can be directly added to the global vector.
Parameters
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- feval (inout)
- values of the field on quadrature points
- res (out)
- result
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh;
MeshNumbering<Dimension3> mesh_num(mesh);
PyramidClassical pyr;
pyr.ConstructFiniteElement(3);
pyr.SetMesh(mesh);
// global results
VectReal_wp res_glob(mesh_num.GetNbDof()); res_glob.Zero();
int num_elem = 15;
// computing transformation Fi for quadrature points
SetPoints<Dimension3> pts; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
pyr.FjElemQuadrature(s, pts, mesh, num_elem);
// computing jacobian matrices DFi for quadrature points
SetMatrices<Dimension3> mat;
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// evaluation of the functions to be treated
// f0 = sin(x+y*z), f1 = cos(x*y - z)
// these functions must be evaluated on quadrature points
int nb_unknowns = 2;
Vector<VectReal_wp> f_eval(nb_unknowns), res_loc;
int N = pyr.GetNbPointsQuadratureInside();
f_eval(0).Reallocate(N); f_eval(1).Reallocate(N);
for (int i = 0; i < N; i++)
{
Real_wp x = pts.GetPointQuadrature(i)(0), y = pts.GetPointQuadrature(i)(1), z = pts.GetPointQuadrature(i)(2);
f_eval(0)(i) = sin(x + y*z); f_eval(1)(i) = cos(x*y - z);
}
// integral against basis functions (on the real element)
pyr.ComputeIntegral(mat, f_eval, res_loc, mesh_num, num_elem);
// then you can add the values on the global vector (here we add only first unknown)
for (int i = 0; i < pyr.GetNbDof(); i++)
res_glob(mesh_num.Element(num_elem).GetNumberDof(i)) += res_loc(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeIntegralGradient
Syntax
| void ComputeIntegralGradient( | const SetMatrices& MatricesElem, Vector<Vector>& feval, Vector<Vector>& res, |
| const MeshNumbering& mesh_num, int num_elem) const |
This method computes the integral of a function over the real element Ke against gradient (or curl/div) of basis functions of the element num_elem:
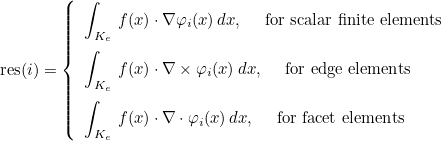
The input array feval contains the evaluation of the function on quadrature points. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in feval(m) where m is the unknown number. The integral is performed with global basis functions, such that the result can be directly added to the global vector.
Parameters
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- feval (inout)
- values of the field on quadrature points
- res (out)
- result
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
Example :
Mesh<Dimension3> mesh;
MeshNumbering<Dimension3> mesh_num(mesh);
PyramidClassical pyr;
pyr.ConstructFiniteElement(3);
pyr.SetMesh(mesh);
// global results
VectReal_wp res_glob(mesh_num.GetNbDof()); res_glob.Zero();
int num_elem = 15;
// computing transformation Fi for quadrature points
SetPoints<Dimension3> pts; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
pyr.FjElemQuadrature(s, pts, mesh, num_elem);
// computing jacobian matrices DFi for quadrature points
SetMatrices<Dimension3> mat;
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// evaluation of the function to be treated
// f = (sin(x+y*z), cos(x*y - z), exp(x+y+z))
// these functions must be evaluated on quadrature points
int nb_unknowns = 1;
Vector<VectReal_wp> f_eval(nb_unknowns), res_loc;
int N = pyr.GetNbPointsQuadratureInside(); f_eval(0).Reallocate(3*N);
for (int i = 0; i < N; i++)
{
Real_wp x = pts.GetPointQuadrature(i)(0), y = pts.GetPointQuadrature(i)(1), z = pts.GetPointQuadrature(i)(2);
f_eval(0)(3*i) = sin(x + y*z); f_eval(0)(3*i+1) = cos(x*y - z); f_eval(0)(3*i+2) = exp(x+y+z);
}
// integral against gradient of basis functions (on the real element)
// for edge elements, gradient is replaced by the curl
pyr.ComputeIntegralGradient(mat, f_eval, res_loc, mesh_num, num_elem);
// then you can add the values on the global vector
for (int i = 0; i < pyr.GetNbDof(); i++)
res_glob(mesh_num.Element(num_elem).GetNumberDof(i)) += res_loc(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeGaussIntegralSurface
Syntax
| void ComputeGaussIntegralSurface( | const Vector<MatrixN_N>& dfjm1, const VectReal_wp& weights, const VectReal_wp& ds, |
| Vector<Vector>& feval, Vector<Vector>& res, const MeshNumbering& mesh_num, int num_elem, int num_loc) const |
This method computes the integral of a function over the boundary num_loc of the real element Ke against basis functions of the element num_elem:
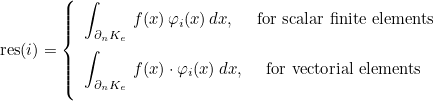
The integral is computed with Gauss-Legendre points (even if the finite element is based on Gauss-Lobatto points), such that the result should be more accurate than with ComputeIntegralSurface. The input array feval contains the evaluation of the function on quadrature points of the boundary. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in feval(m) where m is the unknown number. The integral is performed with global basis functions, such that the result can be directly added to the global vector.
Parameters
- dfjm1 (in)
- list of matrices DFi at quadrature points
- weights (in)
- quadrature weights multiplied by surface element ds
- ds (in)
- surface element ds
- feval (inout)
- values of the field on quadrature points
- res (out)
- result
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
- num_loc (in)
- local boundary number
Example :
Mesh<Dimension3> mesh;
MeshNumbering<Dimension3> mesh_num(mesh);
HexahedronLobatto hex;
hex.ConstructFiniteElement(3);
hex.SetMesh(mesh);
// global results
VectReal_wp res_glob(mesh_num.GetNbDof()); res_glob.Zero();
int num_elem = 15; int num_loc = 2;
// computing transformation Fi for nodal points
SetPoints<Dimension3> pts; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
hex.FjElemNodal(s, pts, mesh, num_elem);
VectR2 points_sq; VectReal_wp weights_sq;
QuadrangleQuadrature::ConstructQuadrature(2*hex.GetOrder(), points_sq, weights_sq);
int N = points_sq.GetM();
Vector<Matrix3_3> dfjm1(N);
VectReal_wp weights(N), ds(N);
// evaluation of the function to be treated
// f = sin(x+y*z)
// these functions must be evaluated on quadrature points
int nb_unknowns = 1; Matrix3_3 dfj; R3 normale;
Vector<VectReal_wp> f_eval(nb_unknowns), res_loc;
f_eval(0).Reallocate(N);
for (int i = 0; i < N; i++)
{
// point in 3-D on the reference element
R3 point_loc, point_glob;
hex.GetLocalCoordOnBoundary(num_loc, points_sq(i), point_loc);
// quadrature point on the real element
hex.Fj(s, pts, point_loc, point_glob, mesh, num_elem);
hex.DFj(s, pts, point_loc, dfj, mesh, num_elem);
GetInverse(dfj, dfjm1(i));
hex.GetNormale(dfjm1(i), normale, ds(i), num_loc);
weights(i) = ds(i)*weights_sq(i);
Real_wp x = point_glob(0), y = point_glob(1), z = point_glob(2);
f_eval(0)(i) = sin(x + y*z);
}
// integral against basis functions (on a boundary of the real element)
hex.ComputeGaussIntegralSurface(dfjm1, weights, ds, f_eval, res_loc, mesh_num, num_elem, num_loc);
// then you can add the values on the global vector
for (int i = 0; i < hex.GetNbDof(); i++)
res_glob(mesh_num.Element(num_elem).GetNumberDof(i)) += res_loc(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeIntegralSurface
Syntax
| void ComputeIntegralSurface( | const SetMatrices& MatricesElem, Vector<Vector>& feval, Vector<Vector>& res, |
| const MeshNumbering& mesh_num, int num_elem, int num_loc) const |
This method computes the integral of a function over the boundary num_loc of the real element Ke against basis functions of the element num_elem:
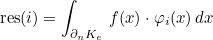
The input array feval contains the evaluation of the function on quadrature points. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in feval(m) where m is the unknown number. The integral is performed with global basis functions, such that the result can be directly added to the global vector.
Parameters
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- feval (inout)
- values of the field on quadrature points
- res (out)
- result
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
- num_loc (in)
- local boundary number
Example :
Mesh<Dimension3> mesh;
MeshNumbering<Dimension3> mesh_num(mesh);
PyramidClassical pyr;
pyr.ConstructFiniteElement(3);
pyr.SetMesh(mesh);
// global results
VectReal_wp res_glob(mesh_num.GetNbDof()); res_glob.Zero();
int num_elem = 15;
// computing transformation Fi for quadrature points
SetPoints<Dimension3> pts; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
pyr.FjElemQuadrature(s, pts, mesh, num_elem);
// computing jacobian matrices DFi for quadrature points
SetMatrices<Dimension3> mat;
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// points on the boundary
int num_loc = 2;
pyr.FjElemSurface(s, pts, mesh, num_elem, num_loc);
pyr.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc);
// evaluation of the functions to be treated
// f0 = sin(x+y*z), f1 = cos(x*y - z)
// these functions must be evaluated on quadrature points
int nb_unknowns = 2;
Vector<VectReal_wp> f_eval(nb_unknowns), res_loc;
int N = pyr.GetNbQuadBoundary(num_loc);
f_eval(0).Reallocate(N); f_eval(1).Reallocate(N);
for (int i = 0; i < N; i++)
{
R3 pt_glob = pts.GetPointQuadratureBoundary(i);
Real_wp x = pt_glob(0), y = pt_glob(1), z = pt_glob(2);
f_eval(0)(i) = sin(x + y*z); f_eval(1)(i) = cos(x*y - z);
}
// integral against basis functions (on the boundary of the real element)
pyr.ComputeIntegralSurface(mat, f_eval, res_loc, mesh_num, num_elem, num_loc);
// then you can add the values on the global vector (here we add only first unknown)
for (int i = 0; i < pyr.GetNbDof(); i++)
res_glob(mesh_num.Element(num_elem).GetNumberDof(i)) += res_loc(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeIntegralSurfaceGradient
Syntax
| void ComputeIntegralSurfaceGradient( | const SetMatrices& MatricesElem, Vector<Vector>& feval, Vector<Vector>& res, |
| const MeshNumbering& mesh_num, int num_elem, int num_loc) const |
This method computes the integral of a function over the boundary num_loc of the real element Ke against gradient (or curl/div) of basis functions of the element num_elem:
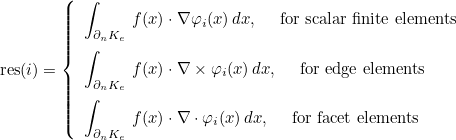
The input array feval contains the evaluation of the function on quadrature points. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in feval(m) where m is the unknown number. The integral is performed with global basis functions, such that the result can be directly added to the global vector.
Parameters
- MatricesElem (in)
- object storing matrices DFi at quadrature points
- feval (inout)
- values of the field on quadrature points
- res (out)
- result
- mesh_num (in)
- mesh numbering
- num_elem (in)
- element number
- num_loc (in)
- local boundary number
Example :
Mesh<Dimension3> mesh;
MeshNumbering<Dimension3> mesh_num(mesh);
PyramidClassical pyr;
pyr.ConstructFiniteElement(3);
pyr.SetMesh(mesh);
// global results
VectReal_wp res_glob(mesh_num.GetNbDof()); res_glob.Zero();
int num_elem = 15;
// computing transformation Fi for quadrature points
SetPoints<Dimension3> pts; VectR3 s;
mesh.GetVerticesElement(num_elem, s);
pyr.FjElemQuadrature(s, pts, mesh, num_elem);
// computing jacobian matrices DFi for quadrature points
SetMatrices<Dimension3> mat;
pyr.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// points on the boundary
int num_loc = 2;
pyr.FjElemSurface(s, pts, mesh, num_elem, num_loc);
pyr.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc);
// evaluation of the function to be treated
// f = (sin(x+y*z), cos(x*y - z), exp(x+y+z))
// these functions must be evaluated on quadrature points
int nb_unknowns = 1;
Vector<VectReal_wp> f_eval(nb_unknowns), res_loc;
int N = pyr.GetNbQuadBoundary(num_loc);
f_eval(0).Reallocate(3*N);
for (int i = 0; i < N; i++)
{
R3 pt_glob = pts.GetPointQuadratureBoundary(i);
Real_wp x = pt_glob(0), y = pt_glob(1), z = pt_glob(2);
f_eval(0)(3*i) = sin(x + y*z); f_eval(0)(3*i+1) = cos(x*y - z); f_eval(0)(3*i+2) = exp(x+y+z);
}
// integral against gradient of basis functions (on a face of the real element)
// for edge elements, gradient is replaced by the curl
pyr.ComputeIntegralSurfaceGradient(mat, f_eval, res_loc, mesh_num, num_elem, num_loc);
// then you can add the values on the global vector
for (int i = 0; i < pyr.GetNbDof(); i++)
res_glob(mesh_num.Element(num_elem).GetNumberDof(i)) += res_loc(i);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeValueBoundary
Syntax
| void ComputeValueBoundary( | const SetMatrices& MatricesElem, Vector<Vector>& u_loc, Vector<Vector>& u_nodal, |
| const Mesh& mesh, int num_elem, int num_loc) const |
This method computes the values of a field for nodal points of the boundary num_loc of the element num_elem. The computation is made on the real element. The input array u_loc contains the components of the field on the degrees of freedom of the element. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in u_loc(m) where m is the unknown number.
Parameters
- MatricesElem (in)
- object storing matrices DFi at nodal points
- u_loc (in)
- components of the field on degrees of freedom of the element
- u_nodal (out)
- result
- mesh (in)
- considered mesh
- num_elem (in)
- element number
- num_loc (in)
- local boundary number
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // global field VectReal_wp u_glob(mesh_num.GetNbDof()); u_glob.FillRand(); // we extract the local components for an element int num_elem = 15; int nb_unknowns = 1; Vector<VectReal_wp> u_loc(1); mesh_num.number_map.GetLocalUnknownVector(mesh_num, u_glob, num_elem, u_loc); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for nodal points SetMatrices<Dimension3> mat; pyr.DFjElemNodal(s, pts, mat, mesh, num_elem); // DFi on nodal points of boundary int num_loc = 1; mat.ComputeNodalBoundary(num_loc, pyr); // values of u on nodal points of a boundary Vector<Vector<TinyVector<Real_wp, 1> > > u_nodal; // number of components is 1 for scalar elements, 2 or 3 for vectorial elements pyr.ComputeValueBoundary(mat, u_loc, u_nodal, mesh, num_elem, num_loc);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeGradientBoundary
Syntax
| void ComputeGradientBoundary( | const SetMatrices& MatricesElem, Vector<Vector>& u_loc, Vector<Vector>& grad_u_nodal, |
| const Mesh& mesh, int num_elem, int num_loc) const |
This method computes the gradient of a field for nodal points of the boundary num_loc of the element num_elem. For edge elements, the gradient is replaced by the curl, and for facet elements by the divergence. The computation is made on the real element. The input array u_loc contains the components of the field on the degrees of freedom of the element. The field can comprise several unknowns, that's why a vector of vectors is required, each unknown is stored in u_loc(m) where m is the unknown number.
Parameters
- MatricesElem (in)
- object storing matrices DFi at nodal points
- u_loc (in)
- components of the field on degrees of freedom of the element
- grad_u_nodal (out)
- result
- mesh (in)
- considered mesh
- num_elem (in)
- element number
- num_loc (in)
- local boundary number
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // global field VectReal_wp u_glob(mesh_num.GetNbDof()); u_glob.FillRand(); // we extract the local components for an element int num_elem = 15; int nb_unknowns = 1; Vector<VectReal_wp> u_loc(1); mesh_num.number_map.GetLocalUnknownVector(mesh_num, u_glob, num_elem, u_loc); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for nodal points SetMatrices<Dimension3> mat; pyr.DFjElemNodal(s, pts, mat, mesh, num_elem); // DFi on nodal points of boundary int num_loc = 1; mat.ComputeNodalBoundary(num_loc, pyr); // gradient of u on nodal points of a boundary Vector<Vector<TinyVector<Real_wp, 3> > > grad_u_nodal; // number of components is 2 or 3 for scalar elements, 1 or 3 for vectorial elements pyr.ComputeGradientBoundary(mat, u_loc, grad_u_nodal, mesh, num_elem, num_loc);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeValueNodalBoundary
Syntax
| void ComputeValueNodalBoundary(const Vector& u_nodal, Vector& u_boundary, int num_loc) const |
This method extracts the values of u on nodal points of the boundary num_loc from values on nodal points of the element.
Parameters
- u_nodal (in)
- values of u on nodal points of the element
- u_boundary (out)
- values of u on nodal points of the selected boundary
- num_loc (in)
- local boundary number
Example :
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // global solution on all the mesh int nb_unknowns = 2; VectReal_wp u_glob(mesh_num.GetNbDof()*nb_unknowns); u_glob.FillRand(); // extracting the local components of the solution on the selected element int num_elem = 40; Vector<VectReal_wp> u_loc(nb_unknowns); mesh_num.number_map.GetLocalUnknownVector(mesh_num, u_glob, num_elem, u_loc); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for nodal points SetMatrices<Dimension3> mat; pyr.DFjElemNodal(s, pts, mat, mesh, num_elem); // computation of the solution on nodal points of the element Vector<VectReal_wp> u_nodal; pyr.ComputeNodalValues(mat, u_loc, u_nodal, mesh, num_elem); // you can compute the value on nodal points of a boundary int num_loc = 1; VectReal_wp u_boundary; pyr.ComputeValueNodalBoundary(u_nodal(0), u_boundary, num_loc);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ComputeLocalProlongation
Syntax
| void ComputeLocalProlongation( | FiniteElementProjector& proj, Matrix<Real_wp>& LocalProlongation, |
| const ElementReference& elt_coarse, const ElementReference& elt_fine) const |
This method computes the prolongation matrix that can be used to compute the prolongation of a field from a coarse order to a fine order. If the fine order is lower than GetMaximalOrderRestriction(), the projection matrix is stored. If the order is higher, the matrix is not stored, and the object proj is filled. To apply the prolongation operator, the method ProjectScalar is called. For the restriction operator, the method TransposeProjectScalar is called.
Parameters
- proj (out)
- projector from the coarse element to the fine element
- LocalProlongation (out)
- projector stored as a matrix
- elt_coarse (in)
- finite element of coarse order
- elt_fine (in)
- finite element of fine order
Example :
HexahedronGauss hex_fine; hex_fine.ConstructFiniteElement(4); HexahedronGauss hex_coarse; hex_coarse.ConstructFiniteElement(2); // prolongation operator Matrix<Real_wp> LocalProlongation; FiniteElementProjector* proj; proj = hex_fine->GetNewNodalInterpolation(); hex_fine.ComputeLocalProlongation(*proj, LocalProlongation, elt_coarse, elt_fine); // example of use for the object proj VectReal_wp Uc(hex_coarse.GetNbDof()); U.FillRand(); VectReal_wp Uf(hex_fine.GetNbDof()); proj->ProjectScalar(Uc, Uf); // prolongation : Uf = P Uc proj->TransposeProjectScalar(Uf, Uc); // restriction : Uc = P^T Uf
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ApplyRotationCyclic
Syntax
| static void ApplyRotationCyclic( | int n, FftInterface<Complex_wp>& fft, Vector& u) |
This method applies a rotation on the provided vector u. This rotation is applied only for vectorial elements (u is not modified for scalar elements). The vector u is replaced by vector v given as
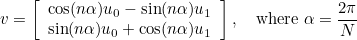
The angle α is provided by the parameter fft.
Parameters
- n (in)
- input integer
- fft (in)
- object storing the angle α
- u (inout)
- vector that will be rotated
Example :
// number of points for FFT int N = 8; FftInterface<Complex_wp> fft; fft.Init(N); // computation of alpha = 2pi/N, sin and cos of this angle // vector to rotate TinyVector<Complex_wp, 3> v; v.Init(complex<double>(0.5, 0.2), complex<double>(2.3, 1.7), complex<double>(-0.4, -1.8)); // applying the rotation int n = 3; // mode number FiniteElementHcurl<Dimension3>::ApplyRotationCyclic(n, fft, v);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx
ApplyInverseRotationCyclic
Syntax
| static void ApplyInverseRotationCyclic( | int n, FftInterface<Complex_wp>& fft, Vector& u) |
This method applies a rotation on the provided vector u. This rotation is applied only for vectorial elements (u is not modified for scalar elements). The vector u is replaced by vector v given as
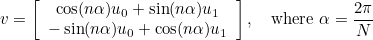
The angle α is provided by the parameter fft.
Parameters
- n (in)
- input integer
- fft (in)
- object storing the angle α
- u (inout)
- vector that will be rotated
Example :
// number of points for FFT int N = 8; FftInterface<Complex_wp> fft; fft.Init(N); // computation of alpha = 2pi/N, sin and cos of this angle // vector to rotate (with angle -n alpha) TinyVector<Complex_wp, 3> v; v.Init(complex<double>(0.5, 0.2), complex<double>(2.3, 1.7), complex<double>(-0.4, -1.8)); // applying the rotation int n = 3; // mode number FiniteElementHcurl<Dimension3>::ApplyInverseRotationCyclic(n, fft, v); // if you have several vectors to rotate, you can put them in a single vector int nb_vec = 2; Vector<Complex_wp> u(3*nb_vec); u(0) = v(0); u(1) = v(1); u(2) = v(2); // first vector to rotate u(3) = complex<double>(2.5, -0.7); u(4) = complex<double>(-2.9, 1.1); u(5) = complex<double>(-2.4, 1.5); // second vector to rotate // the two vectors are rotated FiniteElementHcurl<Dimension3>::ApplyInverseRotationCyclic(n, fft, u);
Location :
FiniteElement/FiniteElementH1.hxx
FiniteElement/FiniteElementH1.cxx
FiniteElement/FiniteElementHcurl2D.hxx
FiniteElement/FiniteElementHcurl2D.cxx
FiniteElement/FiniteElementHcurl3D.hxx
FiniteElement/FiniteElementHcurl3D.cxx
FiniteElement/FiniteElementHdiv.hxx
FiniteElement/FiniteElementHdiv.cxx