Transformation Fi
In this page, we detail the classes related to the transformation Fi. We also detail finite element projectors, that enable to interpolate the solution on predefined sets of points. The transformation Fi transforms a reference element (unit triangle, unit square, unit tetrahedron, symmetric pyramid, unit prism, unit cube) into the real element as shown in the figures below (in 3-D)
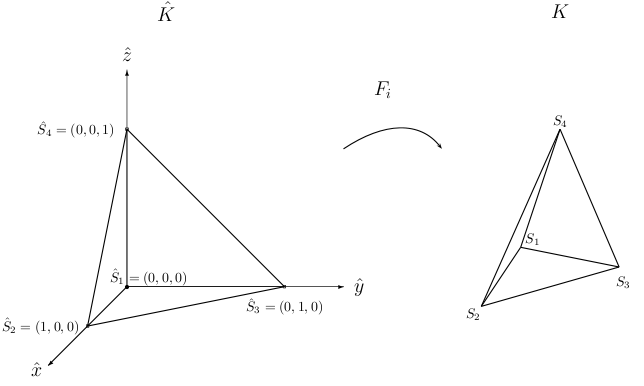 |
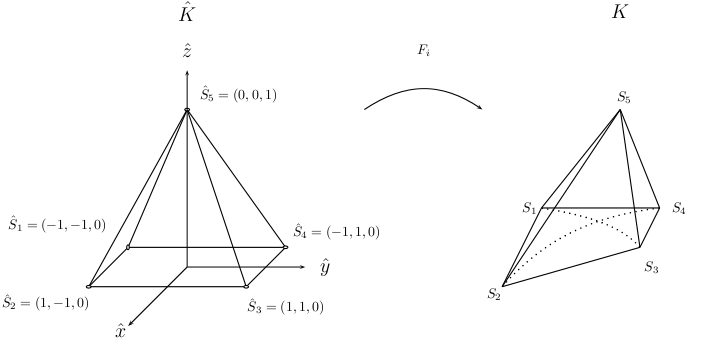 |
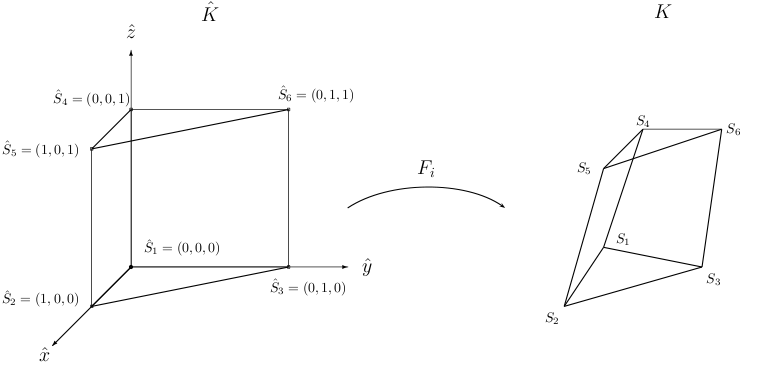 |
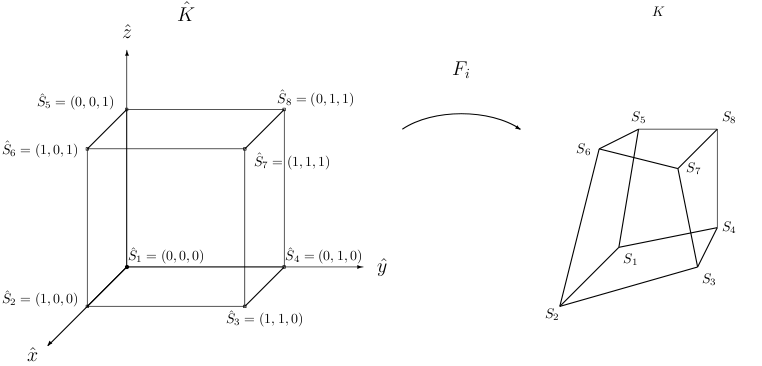 |
The real element can be "straight", i.e. defined with first-order shape functions, or "curved". In that case, we use high-order shape functions to write transformation Fi. When the element is straight, we just need the vertices of the element in order to define the transform, whereas for curved elements, we need intermediary points on the edges and the faces (points placed on the interior are automatically computed). These informations are provided by the mesh.
Usually, we consider three different sets of points which are known on the reference element :
- Nodal points : points used for the expression of transformation Fi when the element is curved
- Quadrature points : points used for integration over the reference element
- Dof (degrees of freedom) points : points used to project a function f to the finite element space. For nodal elements, this will be interpolation points.
Since these points are known, some precomputations are made in finite element classes, so that the computation of transform Fi for these points is fast. The object that effectively stores the images of points by transformation Fi is SetPoints, the jacobian matrices are stored in SetMatrices (see file FiniteElement/PointsReference.hxx), see below an example of use of these classes :
// first you need to define a mesh
Mesh<Dimension2> mesh;
mesh.SetGeometryOrder(4);
// then you read it
mesh.Read("test.mesh");
// you want to know Fi(xi_j) and DF_i(xi_j) for points xi_j
SetPoints<Dimension2> PointsElem;
SetMatrices<Dimension2> MatricesElem;
VectR3 s;
for (int i = 0; i < mesh.GetNbElt(); i++)
{
// first step : retrieve the vertices of the element i
mesh.GetVerticesElement(i, s);
// we retrieve the finite element associated with the element i
const ElementGeomReference<Dimension2>& elt = mesh.GetReferenceElement(i);
// then you ask to compute image of all the points (quadrature, nodal, dofs)
// if you only need nodal points => FjElemNodal
// if you only need quadrature points => FjElemQuadrature
// if you only need dof points => FjElemDof
elt.FjElem(s, PointsElem, mesh, i);
// then you can loop over nodal points
for (int j = 0; j < PointsElem.GetNbPointsNodal(); j++)
cout << PointsElem.GetPointNodal(j) << endl;
// or quadrature points
for (int j = 0; j < PointsElem.GetNbPointsQuadrature(); j++)
cout << PointsElem.GetPointQuadrature(j) << endl;
// or dof points
for (int j = 0; j < PointsElem.GetNbPointsDof(); j++)
cout << PointsElem.GetPointDof(j) << endl;
// you can require the computation of jacobian matrices
elt.DFjElemNodal(s, PointsElem, MatricesElem, mesh, i);
// and display jacobian matrix DFi at each nodal point for instance
for (int j = 0; j < PointsElem.GetNbPointsNodal(); j++)
cout << MatricesElem.GetPointNodal(j) << endl;
// once you have compute FjElemNodal (minimal requirement)
// you can compute Fi(x) for a single point, and DFi(x)
R2 point_local, point global;
point_local.Init(0.5, 0.4);
elt.Fj(s, PointsElem, point_local, point_global, mesh, i);
cout << "The result of Fi(0.5, 0.4) is " << point_global << endl;
Matrix2_2 dfj;
elt.DFj(s, PointsElem, point_local, dfj, mesh, i);
// you can try to invert transformation (using Newton or Minpack solver)
R2 sol_point;
FjInverseProblem<Dimension2> invFj(mesh, i); // here nodal points are computed, no need to call FjElemNodal or FjElem
// inside_elt should be equal to true if the point has been found inside the element
bool inside_elt = inverseFj.Solve(point_global, sol_point);
// you can also compute the image of quadrature points only on the surface
// num_loc is the local number of the surface in the element
int num_loc = 2;
tet.FjSurfaceElem(s, PointsElem, mesh, i, num_loc);
// and jacobian matrices too
tet.DFjSurfaceElem(s, PointsElem, MatricesElem, mesh, i, num_loc);
// then you can display them
for (int i = 0; i < PointsElem.GetNbPointsQuadratureBoundary(); i++)
{
cout << PointsElem.GetPointQuadratureBoundary(i) << endl;
cout << MatricesElem.GetPointQuadratureBoundary(i) << endl;
}
// you can also retrieve normales, and surfacic elements
for (int i = 0; i < PointsElem.GetNbPointsQuadratureBoundary(); i++)
{
// outward normale to the element
R3 normale = MatricesElem.GetNormaleQuadratureBoundary(i);
// surfacic element (for integration)
double ds = MatricesElem.GetDsQuadratureBoundary(i);
}
}
Methods of SetPoints
| ReallocatePointsDof | allocates the array containing dof points |
| ReallocatePointsQuadrature | allocates the array containing quadrature points |
| ReallocatePointsNodal | allocates the array containing nodal points |
| ReallocatePointsQuadratureBoundary | allocates the array containing quadrature points on a face of the element |
| ReallocatePointsDofBoundary | allocates the array containing dof points on a face of the element |
| SetPointDof | sets i-th dof point on the real element |
| SetPointQuadrature | sets i-th quadrature point on the real element |
| SetPointNodal | sets i-th nodal point on the real element |
| SetPointQuadratureBoundary | sets i-th quadrature point on a face of the real element |
| SetPointDofBoundary | sets i-th dof point on a face of the real element |
| GetNbPointsDof | returns the number of dof points |
| GetNbPointsQuadrature | returns the number of quadrature points |
| GetNbPointsNodal | returns the number of nodal points |
| GetNbPointsQuadratureBoundary | returns the number of quadrature points on a face of the element |
| GetNbPointsDofBoundary | returns the number of dof points on a face of the element |
| GetPointDof | returns i-th dof point on the real element |
| GetPointQuadrature | returns i-th quadrature point on the real element |
| GetPointNodal | returns i-th nodal point on the real element |
| GetPointQuadratureBoundary | returns i-th quadrature point on a face of the real element |
| GetPointDofBoundary | returns i-th dof point on a face of the real element |
| CopyNodalToQuadrature | quadrature points are the same as nodal points |
| CopyNodalToDof | dof points are the same as nodal points |
| CopyQuadratureToDof | dof points are the same as quadrature points |
| RotatePoints | applies rotation to points with respect to z-axis |
| TranslatePoints | applies translation to points |
Methods of SetMatrices
| ReallocatePointsDof | allocates the array containing matrices on dof points |
| ReallocatePointsQuadrature | allocates the array containing matrices on quadrature points |
| ReallocatePointsNodal | allocates the array containing matrices on nodal points |
| ReallocatePointsQuadratureBoundary | allocates the array containing matrices on quadrature points on a face of the element |
| ReallocatePointsDofBoundary | allocates the array containing matrices on dof points on a face of the element |
| GetNbPointsQuadratureBoundary | returns the number of quadrature points on a face of the element |
| GetNbPointsDofBoundary | returns the number of dof points on a face of the element |
| SetPointDof | sets the jacobian matrix for the i-th dof point |
| SetPointQuadrature | sets the jacobian matrix for the i-th quadrature point |
| SetPointNodal | sets the jacobian matrix for the i-th nodal point |
| SetPointQuadratureBoundary | sets the jacobian matrix for the i-th quadrature point on a face |
| SetPointDofBoundary | sets the jacobian matrix for the i-th quadrature point on a face |
| SetPointNodalBoundary | sets the jacobian matrix for the i-th nodal point on a face |
| SetInversePointNodalBoundary | sets the inverse of jacobian matrix for the i-th nodal point on a face |
| SetNormaleQuadratureBoundary | sets the outward normale for the i-th quadrature point on a face |
| SetDsQuadratureBoundary | sets the element of surface integration for a quadrature point of a face |
| SetK1QuadratureBoundary | sets the first eigenvalue of curvature tensor for a quadrature point of a face |
| SetK2QuadratureBoundary | sets the second eigenvalue of curvature tensor for a quadrature point of a face |
| FillNodal | sets all jacobian matrices for nodal points to a same matrix |
| FillQuadrature | sets all jacobian matrices for quadrature points to a same matrix |
| FillDof | sets all jacobian matrices for dof points to a same matrix |
| ComputeNodalBoundary | computes jacobian matrices for nodal points of a face |
| GetPointDof | returns the jacobian matrix for the i-th dof point |
| GetPointQuadrature | returns the jacobian matrix for the i-th quadrature point |
| GetPointNodal | returns the jacobian matrix for the i-th nodal point |
| GetPointQuadratureBoundary | returns the jacobian matrix for the i-th quadrature point on a face |
| GetPointDofBoundary | returns the jacobian matrix for the i-th dof point on a face |
| GetNormaleQuadratureBoundary | returns the outward normale for the i-th quadrature point on a face |
| GetPointNodalBoundary | returns the jacobian matrix for nodal points of a face |
| GetInversePointNodalBoundary | returns the inverse of jacobian matrix for nodal points of a face |
| GetDsQuadratureBoundary | returns the element of surface integration for a quadrature point of a face |
| GetK1QuadratureBoundary | returns the first eigenvalue of curvature tensor for a quadrature point of a face |
| GetK2QuadratureBoundary | returns the second eigenvalue of curvature tensor for a quadrature point of a face |
| CopyNodalToQuadrature | jacobian matrices for quadrature points are the same as for nodal points |
| CopyNodalToDof | jacobian matrices for dof points are the same as for nodal points |
| CopyQuadratureToDof | jacobian matrices for dof points are the same as for quadrature points |
| RotateNormale | applies rotation to normales with respect to z-axis |
| InitSetPoints | associates a set of points with the current object |
| GetSetPoints | returns the associated set of points |
Attributes and methods of FjInverseProblem
Below we list the attributes and methods of the class FjInverseProblem, which is used to compute the solution x of the equation Fi(x) = y.
| non_linear_solver | which non-linear solver has to be used to solve the equation |
| nb_max_iterations | maximum number of iterations allowed to find the solution |
| threshold_newton | stopping criterion used by non-linear solvers |
| coef_safety_solver | coefficient used to determine if the computed solution is outside the reference element |
| GetVertices | returns the vertices of the element |
| GetSetPoints | returns the nodal points of the element |
| Solve | computes the solution and returns true if the point is outside the reference element |
Projection on other sets of points
It is often needed to project a finite element solution on a set of points. The base class FiniteElementProjector does this task from nodal shape functions. The derived classes TensorizedProjector and DenseProjector are implementations of this base class. In the class TensorizedProjector, the projection matrix is stored as a product of sparse matrices because of tensorization of points. In the class DenseProjector, there is no tensorization and the projection matrix is stored as a dense matrix. Finally the class FiniteElementInterpolator stores projectors for the different elements at a given order. For example, in 3-D it will store four projectors (one for tetrahedra, one for pyramids, one for prisms and one for hexahedra). Below, we provide some basic examples of use of these classes
// case of a dense projector (e.g. with triangles)
TriangleGeomReference tri;
tri.ConstructFiniteElement(4);
// definition of points where we want to interpolate the solution
VectR2 pts_interp(10);
pts_interp(0).Init(0.4, 0.7);
pts_interp(1).Init(0.2, 0.9);
// etc
// computation of the projector
DenseProjector<Dimension2> proj;
proj.Init(tri, pts_interp);
// then you can use it to compute the interpolation on the provided points
VectReal_wp u(tri.GetNbPointsNodalElt());
u.FillRand();
VectReal_wp u_interp;
proj.Project(u, u_interp); // u_interp is the value of the field on the interpolated points
// if you want to apply the transpose operator :
VectReal_wp v_interp(pts_interp.GetM());
v_interp.FillRand();
proj.TransposeProject(v_interp, v); // computation of v = P^T v_interp
// if you want a generic writing (for triangles/quads), use a pointer
FiniteElementProjector* p;
p = tri.GetNewNodalInterpolation(); // it will create a DenseProjector or TensorizedProjector
// Init, Project and TransposeProject can be called similarly
p->Init(tri, pts_interp);
p->Project(u, u_interp);
// for mixed meshes, you can use FiniteElementInterpolator
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
Vector<VectR3> pts_3d(4);
// points for the unit tetrahedron
pts_3d(0).Reallocate(5);
pts_3d(0)(0).Init(0.2, 0.2, 0.1); // etc
// for the symmetric pyramid
pts_3d(1).Reallocate(10);
pts_3d(1)(0).Init(-0.3, 0.4, 0.2); // etc
// pts_3d(2) for the prism and pts_3d(3) for the pyramid
// in 2-D, pts(0) for the unit triangle and pts(1) for the unit square
// computing the projection for all elements (tet, pyramids, hex, prisms)
FiniteElementInterpolator liste_proj;
liste_proj.InitProjection(mesh.GetReferenceElement(), pts_3d);
// projection for an element :
int num_elem = 12;
liste_proj.Project(u, u_interp, mesh.Element(num_elem).GetHybridType());
Methods of FiniteElementProjector
| SetIdentity | inits the projector as a permutation matrix |
| Project | projects the field on interpolation points |
| TransposeProject | performs the transpose operation of Project |
| GetMemorySize | returns the memory used by the object in bytes |
| Init | computes the projection operator |
| ProjectScalar | projects a scalar field on interpolation points |
| TransposeProjectScalar | projects a scalar field on interpolation points |
Methods of FiniteElementInterpolator
| InitProjection | computes the projection operators |
| Project | projects the field on interpolation points |
| TransposeProject | performs the transpose operation of Project |
| ProjectScalar | projects a scalar field on interpolation points |
| TransposeProjectScalar | projects a scalar field on interpolation points |
| ComputeLocalProlongation | computes the prolongation operator between two finite elements |
| ComputeLocalProlongationLowOrder | computes the prolongation operator between two finite elements by using first-order elements |
ReallocatePointsDof
Syntax
| void ReallocatePointsDof( | int n) |
This method reallocates the array containing points associated with degrees of freedom. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsDof(N); // allocating the array // filling the array pts.SetPointDof(0, R3(0.4, 0.7, 0.2)); pts.SetPointDof(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ReallocatePointsQuadrature
Syntax
| void ReallocatePointsQuadrature( | int n) |
This method reallocates the array containing quadrature points of the element. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsQuadrature(N); // allocating the array // filling the array pts.SetPointQuadrature(0, R3(0.4, 0.7, 0.2)); pts.SetPointQuadrature(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ReallocatePointsNodal
Syntax
| void ReallocatePointsNodal( | int n) |
This method reallocates the array containing nodal points. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsNodal(N); // allocating the array // filling the array pts.SetPointNodal(0, R3(0.4, 0.7, 0.2)); pts.SetPointNodal(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ReallocatePointsQuadratureBoundary
Syntax
| void ReallocatePointsQuadratureBoundary( | int n) |
This method reallocates the array containing the quadrature points of a boundary of the element. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsQuadratureBoundary(N); // allocating the array // filling the array pts.SetPointQuadratureBoundary(0, R3(0.4, 0.7, 0.2)); pts.SetPointQuadratureBoundary(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ReallocatePointsDofBoundary
Syntax
| void ReallocatePointsDofBoundary( | int n) |
This method reallocates the array containing points associated with degrees of freedom of the boundary. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsDofBoundary(N); // allocating the array // filling the array pts.SetPointDofBoundary(0, R3(0.4, 0.7, 0.2)); pts.SetPointDofBoundary(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointDof
Syntax
| void SetPointDof( | int i, | R_N point) |
This method modifies the i-th point associated with degrees of freedom. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsDof(N); // allocating the array // filling the array pts.SetPointDof(0, R3(0.4, 0.7, 0.2)); pts.SetPointDof(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointQuadrature
Syntax
| void SetPointQuadrature( | int i, R_N point) |
This method sets the i-th quadrature point of the element. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsQuadrature(N); // allocating the array // filling the array pts.SetPointQuadrature(0, R3(0.4, 0.7, 0.2)); pts.SetPointQuadrature(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointNodal
Syntax
| void SetPointNodal( | int i, R_N point) |
This method sets the i-th nodal point of the element. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsNodal(N); // allocating the array // filling the array pts.SetPointNodal(0, R3(0.4, 0.7, 0.2)); pts.SetPointNodal(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointQuadratureBoundary
Syntax
| void SetPointQuadratureBoundary( | int i, R_N point) |
This method sets the i-th quadrature point of a boundary of the element. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsQuadratureBoundary(N); // allocating the array // filling the array pts.SetPointQuadratureBoundary(0, R3(0.4, 0.7, 0.2)); pts.SetPointQuadratureBoundary(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointDofBoundary
Syntax
| void SetPointDofBoundary( | int i, | R_N point) |
This method modifies the i-th point associated with degrees of freedom of the boundary. In a regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsDofBoundary(N); // allocating the array // filling the array pts.SetPointDofBoundary(0, R3(0.4, 0.7, 0.2)); pts.SetPointDofBoundary(1, R3(0.8, -0.2, 1.5)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNbPointsDof
Syntax
| int GetNbPointsDof() const |
This method returns the number of points associated with degrees of freedom.
Example
// finite element is constructed
WedgeClassical wed;
wed.ConstructFiniteElement(3);
wed.SetMesh(mesh);
// computing transformation Fi for dof points
SetPoints<Dimension3> pts;
VectR3 s; int num_elem = 40;
mesh.GetVerticesElement(num_elem, s);
wed.FjElemDof(s, pts, mesh, num_elem);
// you can retrieve the number of dof points stored in pts
int nb_pts = pts.GetNbPointsDof();
// loop over these points
for (int i = 0; i < nb_pts; i++)
cout << "Dof point " << i << " = " << pts.GetPointDof(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNbPointsQuadrature
Syntax
| int GetNbPointsQuadrature() const |
This method returns the number of quadrature points stored in the object.
Example
// finite element is constructed
WedgeClassical wed;
wed.ConstructFiniteElement(3);
wed.SetMesh(mesh);
// computing transformation Fi for quadrature points
SetPoints<Dimension3> pts;
VectR3 s; int num_elem = 40;
mesh.GetVerticesElement(num_elem, s);
wed.FjElemQuadrature(s, pts, mesh, num_elem);
// you can retrieve the number of quadrature points stored in pts
int nb_pts = pts.GetNbPointsQuadrature();
// loop over these points
for (int i = 0; i < nb_pts; i++)
cout << "Quadrature point " << i << " = " << pts.GetPointQuadrature(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNbPointsNodal
Syntax
| int GetNbPointsNodal() const |
This method returns the number of nodal points stored in the object.
Example
// finite element is constructed
WedgeClassical wed;
wed.ConstructFiniteElement(3);
wed.SetMesh(mesh);
// computing transformation Fi for nodal points
SetPoints<Dimension3> pts;
VectR3 s; int num_elem = 40;
mesh.GetVerticesElement(num_elem, s);
wed.FjElemNodal(s, pts, mesh, num_elem);
// you can retrieve the number of nodal points stored in pts
int nb_pts = pts.GetNbPointsNodal();
// loop over these points
for (int i = 0; i < nb_pts; i++)
cout << "Nodal point " << i << " = " << pts.GetPointNodal(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNbPointsQuadratureBoundary
Syntax
| int GetNbPointsQuadratureBoundary() const |
This method returns the number of quadrature points associated with a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // and quadrature points of the boundary int num_loc = 2; wed.FjElemSurface(s, pts, mesh, num_elem, num_loc); // you can retrieve the number of boundary quadrature points stored in pts int nb_pts = pts.GetNbPointsQuadratureBoundary(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Boundary quadrature point " << i << " = " << pts.GetPointQuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNbPointsDofBoundary
Syntax
| int GetNbPointsDofBoundary() const |
This method returns the number of points associated with degrees of freedom of the boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for dof points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemDof(s, pts, mesh, num_elem); // we extract dof points for a given boundary int num_loc = 2; wed.FjElemSurfaceDof(s, pts, mesh, num_elem, num_loc); // you can retrieve the number of boundary dof points stored in pts int nb_pts = pts.GetNbPointsDofBoundary(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Boundary dof point " << i << " = " << pts.GetPointDofBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointDof
Syntax
| const R_N& GetPointDof(int i) const |
This method returns the i-th point associated with degrees of freedom.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for dof points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemDof(s, pts, mesh, num_elem); // you can retrieve the number of dof points stored in pts int nb_pts = pts.GetNbPointsDof(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Dof point " << i << " = " << pts.GetPointDof(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointQuadrature
Syntax
| const R_N& GetPointQuadrature(int i) const |
This method returns the i-th quadrature point stored in the object.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // you can retrieve the number of quadrature points stored in pts int nb_pts = pts.GetNbPointsQuadrature(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Quadrature point " << i << " = " << pts.GetPointQuadrature(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointNodal
Syntax
| const R_N& GetPointNodal(int i) const |
This method returns the i-th nodal point stored in the object.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // you can retrieve the number of nodal points stored in pts int nb_pts = pts.GetNbPointsNodal(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Nodal point " << i << " = " << pts.GetPointNodal(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointQuadratureBoundary
Syntax
| const R_N& GetPointQuadratureBoundary(int i) const |
This method returns the i-th quadrature point associated with a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // and quadrature points of the boundary int num_loc = 2; wed.FjElemSurface(s, pts, mesh, num_elem, num_loc); // you can retrieve the number of boundary quadrature points stored in pts int nb_pts = pts.GetNbPointsQuadratureBoundary(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Boundary quadrature point " << i << " = " << pts.GetPointQuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointDofBoundary
Syntax
| const R_N& GetPointDofBoundary(int i) const |
This method returns the i-th point associated with degrees of freedom of the boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for dof points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemDof(s, pts, mesh, num_elem); // we extract dof points for a given boundary int num_loc = 2; wed.FjElemSurfaceDof(s, pts, mesh, num_elem, num_loc); // you can retrieve the number of boundary dof points stored in pts int nb_pts = pts.GetNbPointsDofBoundary(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Boundary dof point " << i << " = " << pts.GetPointDofBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
CopyNodalToQuadrature
Syntax
| void CopyNodalToQuadrature() |
This method copies nodal points to quadrature points. On regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsNodal(N); // allocating the array // filling the array pts.SetPointNodal(0, R3(0.4, 0.7, 0.2)); pts.SetPointNodal(1, R3(0.8, -0.2, 1.5)); // etc // if nodal points coincide with quadrature points pts.CopyNodalToQuadrature();
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
CopyNodalToDof
Syntax
| void CopyNodalToDof() |
This method copies nodal points to dof points. On regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsNodal(N); // allocating the array // filling the array pts.SetPointNodal(0, R3(0.4, 0.7, 0.2)); pts.SetPointNodal(1, R3(0.8, -0.2, 1.5)); // etc // if nodal points coincide with dof points pts.CopyNodalToDof();
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
CopyQuadratureToDof
Syntax
| void CopyQuadratureToDof() |
This method copies quadrature points to dof points. On regular use, this method should not be called.
Example
SetPoints<Dimension3> pts; int N = 10; pts.ReallocatePointsQuadrature(N); // allocating the array // filling the array pts.SetPointQuadrature(0, R3(0.4, 0.7, 0.2)); pts.SetPointQuadrature(1, R3(0.8, -0.2, 1.5)); // etc // if quadrature points coincide with dof points pts.CopyQuadratureToDof();
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
RotatePoints
Syntax
| void RotatePoints(Real_wp teta) |
This method rotates points of an angle θ. The axis of rotation if the Ez axis, the new coordinates of the points are given as:
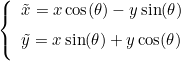
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElem(s, pts, mesh, num_elem); // you can rotate all points pts.RotatePoints(pi_wp/3);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
TranslatePoints
Syntax
| void TranslatePoints(R_N u) |
This method translates points with a vector u.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElem(s, pts, mesh, num_elem); // you can translate all points pts.TranslatePoints(R3(1.0, 0.2, -3.0));
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
ReallocatePointsDof
Syntax
| void ReallocatePointsDof( | int n) |
This method reallocates the array containing jacobian matrices associated with degrees of freedom. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsDof(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointDof(0, A0); mat.SetPointDof(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ReallocatePointsQuadrature
Syntax
| void ReallocatePointsQuadrature( | int n) |
This method reallocates the array containing jacobian matrices associated with quadrature points. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsQuadrature(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointQuadrature(0, A0); mat.SetPointQuadrature(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ReallocatePointsNodal
Syntax
| void ReallocatePointsNodal( | int n) |
This method reallocates the array containing jacobian matrices associated with nodal points. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsNodal(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointNodal(0, A0); mat.SetPointNodal(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ReallocatePointsQuadratureBoundary
Syntax
| void ReallocatePointsQuadratureBoundary( | int n) |
This method reallocates the array containing jacobian matrices associated with quadrature points of a face. It also reallocates the array containing normales and surface elements. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsQuadratureBoundary(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointQuadratureBoundary(0, A0); mat.SetPointQuadratureBoundary(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
ReallocatePointsDofBoundary
Syntax
| void ReallocatePointsDofBoundary( | int n) |
This method reallocates the array containing jacobian matrices associated with dof points of a face. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsDofBoundary(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointDofBoundary(0, A0); mat.SetPointDofBoundary(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNbPointsQuadratureBoundary
Syntax
| int GetNbPointsQuadratureBoundary() const |
This method returns the number of quadrature points associated with a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // and jacobian wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // and quadrature points of the boundary int num_loc = 2; wed.FjElemSurface(s, pts, mesh, num_elem, num_loc); wed.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc); // you can retrieve the number of boundary quadrature points stored in mat int nb_pts = mat.GetNbPointsQuadratureBoundary(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Boundary quadrature point " << i << " = " << pts.GetPointQuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNbPointsDofBoundary
Syntax
| int GetNbPointsDofBoundary() const |
This method returns the number of dof points associated with a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for dof points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemDof(s, pts, mesh, num_elem); // and jacobian wed.DFjElemDof(s, pts, mat, mesh, num_elem); // and quadrature points of the boundary int num_loc = 2; wed.FjElemSurfaceDof(s, pts, mesh, num_elem, num_loc); wed.DFjElemSurfaceDof(s, pts, mat, mesh, num_elem, num_loc); // you can retrieve the number of boundary dof points stored in mat int nb_pts = mat.GetNbPointsDofBoundary(); // loop over these points for (int i = 0; i < nb_pts; i++) cout << "Boundary dof point " << i << " = " << pts.GetPointDofBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointDof
Syntax
| void SetPointDof( | int i, | MatrixN_N A) |
This method modifies the i-th jacobian matrix associated with degrees of freedom. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsDof(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointDof(0, A0); mat.SetPointDof(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointQuadrature
Syntax
| void SetPointQuadrature( | int i, | MatrixN_N A) |
This method modifies the i-th jacobian matrix associated with quadrature points. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsQuadrature(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointQuadrature(0, A0); mat.SetPointQuadrature(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointNodal
Syntax
| void SetPointNodal( | int i, | MatrixN_N A) |
This method modifies the i-th jacobian matrix associated with nodal points. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsNodal(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointNodal(0, A0); mat.SetPointNodal(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointQuadratureBoundary
Syntax
| void SetPointQuadratureBoundary( | int i, | MatrixN_N A) |
This method modifies the i-th jacobian matrix associated with quadrature points of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsQuadratureBoundary(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointQuadratureBoundary(0, A0); mat.SetPointQuadratureBoundary(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointDofBoundary
Syntax
| void SetPointDofBoundary( | int i, | MatrixN_N A) |
This method modifies the i-th jacobian matrix associated with dof points of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsDofBoundary(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointDofBoundary(0, A0); mat.SetPointDofBoundary(1, A1); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetPointNodalBoundary
Syntax
| void SetPointNodalBoundary( | Vector<MatrixN_N> vecA) |
This method sets all the jacobian matrices associated with nodal points of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; // filling the array of jacobian matrices Vector<Matrix2_2> A(2); A(0)(0, 0) = 0.4; A(0)(0, 1) = 2.0; A(0)(1, 0) = -1.6; A(0)(1, 1) = 2.5; A(1)(0, 0) = 0.8; A(1)(0, 1) = 1.9; A(1)(1, 0) = -2.3; A(1)(1, 1) = 3.2; // all the matrices are provided once mat.SetPointNodalBoundary(A);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetInversePointNodalBoundary
Syntax
| void SetInversePointNodalBoundary( | Vector<MatrixN_N> vecA) |
This method sets the inverse of all the jacobian matrices associated with nodal points of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat;
// filling the array of jacobian matrices
Vector<Matrix2_2> A(2);
A(0)(0, 0) = 0.4; A(0)(0, 1) = 2.0; A(0)(1, 0) = -1.6; A(0)(1, 1) = 2.5;
A(1)(0, 0) = 0.8; A(1)(0, 1) = 1.9; A(1)(1, 0) = -2.3; A(1)(1, 1) =
3.2;
// all the matrices are provided once
mat.SetPointNodalBoundary(A);
// you can also compute the inverses
for (int i = 0; i < A.GetM(); i++)
GetInverse(A(i));
// and provide these inverses
mat.SetInversePointNodalBoundary(A);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetNormaleQuadratureBoundary
Syntax
| void SetNormaleQuadratureBoundary( | int i, | R_N normale) |
This method modifies the i-th outgoing normale associated with quadrature points of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension3> mat; int N = 10; mat.ReallocatePointsQuadratureBoundary(N); // allocating the needed arrays // filling the normales mat.SetNormaleQuadratureBoundary(0, R3(0.8, 0.5, 0.2)); mat.SetNormaleQuadratureBoundary(1, R3(0.7, 0.82, -0.3)); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetDsQuadratureBoundary
Syntax
| void SetDsQuadratureBoundary( | int i, | Real_wp ds) |
This method modifies the i-th surface element associated with quadrature points of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension3> mat; int N = 10; mat.ReallocatePointsQuadratureBoundary(N); // allocating the needed arrays // filling the normales and surface elements mat.SetNormaleQuadratureBoundary(0, R3(0.8, 0.5, 0.2)); mat.SetDsQuadratureBoundary(0, 0.23); mat.SetNormaleQuadratureBoundary(1, R3(0.7, 0.82, -0.3)); mat.SetDsQuadratureBoundary(1, 0.35); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetK1QuadratureBoundary
Syntax
| void SetK1QuadratureBoundary( | int i, | Real_wp k1) |
This method modifies the first eigenvalue of the curvature tensor associated with the i-th quadrature point of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension3> mat; int N = 10; mat.ReallocatePointsQuadratureBoundary(N); // allocating the needed arrays // filling the eigenvalues of the curvature tensor mat.SetK1QuadratureBoundary(0, 0.5); mat.SetK2QuadratureBoundary(0, 0.23); mat.SetK1QuadratureBoundary(1, 0.45); mat.SetK2QuadratureBoundary(1, 0.35); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
SetK2QuadratureBoundary
Syntax
| void SetK2QuadratureBoundary( | int i, | Real_wp k2) |
This method modifies the second eigenvalue of the curvature tensor associated with the i-th quadrature point of a boundary. In a regular use, this method should not be called.
Example
SetMatrices<Dimension3> mat; int N = 10; mat.ReallocatePointsQuadratureBoundary(N); // allocating the needed arrays // filling the eigenvalues of the curvature tensor mat.SetK1QuadratureBoundary(0, 0.5); mat.SetK2QuadratureBoundary(0, 0.23); mat.SetK1QuadratureBoundary(1, 0.45); mat.SetK2QuadratureBoundary(1, 0.35); // etc
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
FillNodal
Syntax
| void FillNodal( | MatrixN_N A) |
This method sets all the jacobian matrices associated with nodal points with a given matrix. This method is called by finite element classes when the transformation Fi is linear. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsNodal(N); // allocating the needed arrays // filling the array of jacobian matrices with a constant matrix Matrix2_2 A; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; mat.FillNodal(A);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
FillQuadrature
Syntax
| void FillQuadrature( | MatrixN_N A) |
This method sets all the jacobian matrices associated with quadrature points with a a given matrix. This method is called by finite element classes when the transformation Fi is linear. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsQuadrature(N); // allocating the needed arrays // filling the array of jacobian matrices with a constant matrix Matrix2_2 A; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; mat.FillQuadrature(A);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
FillDof
Syntax
| void FillDof( | MatrixN_N A) |
This method sets all the jacobian matrices associated with dof points with a a given matrix. This method is called by finite element classes when the transformation Fi is linear. In a regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsDof(N); // allocating the needed arrays // filling the array of jacobian matrices with a constant matrix Matrix2_2 A; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; mat.FillDof(A);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
ComputeNodalBoundary
Syntax
| void ComputeNodalBoundary( | int num_loc, const ElementReference& elt) |
This method fills the jacobian matrices associated with nodal points of a boundary. It uses the finite element class to retrieve the numbers of nodal points located on the boundary num_loc.
Example
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points int num_elem = 32; SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for nodal points SetMatrices<Dimension3> mat; pyr.DFjElemNodal(s, pts, mat, mesh, num_elem); // DFi on nodal points of boundary int num_loc = 1; mat.ComputeNodalBoundary(num_loc, pyr); // you can retrieve a jacobian matrix on a nodal point of the boundary int j = 2; // local number of the nodal point on the boundary Matrix3_3 dfj = mat.GetPointNodalBoundary(j);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointDof
Syntax
| const MatrixN_N& GetPointDof(int i) const |
This method returns the i-th jacobian matrix associated with degrees of freedom.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for dof points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemDof(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElemDof(s, pts, mat, mesh, num_elem); // you can retrieve the number of dof points stored in pts int nb_pts = pts.GetNbPointsDof(); // and display jacobian matrices for (int i = 0; i < nb_pts; i++) cout << "Jacobian matrix " << i << " = " << mat.GetPointDof(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointQuadrature
Syntax
| const MatrixN_N& GetPointQuadrature(int i) const |
This method returns the jacobian matrix associated with the i-th quadrature point.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // you can retrieve the number of quadrature points stored in pts int nb_pts = pts.GetNbPointsQuadrature(); // and display jacobian matrices for (int i = 0; i < nb_pts; i++) cout << "Jacobian matrix " << i << " = " << mat.GetPointQuadrature(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointNodal
Syntax
| const MatrixN_N& GetPointNodal(int i) const |
This method returns the jacobian matrix associated with the i-th nodal point.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for nodal points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemNodal(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElemNodal(s, pts, mat, mesh, num_elem); // you can retrieve the number of nodal points stored in pts int nb_pts = pts.GetNbPointsNodal(); // and display jacobian matrices for (int i = 0; i < nb_pts; i++) cout << "Jacobian matrix " << i << " = " << mat.GetPointNodal(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointQuadratureBoundary
Syntax
| const MatrixN_N& GetPointQuadratureBoundary(int i) const |
This method returns the jacobian matrix associated with the i-th quadrature point of a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // and quadrature points of the boundary int num_loc = 2; wed.FjElemSurface(s, pts, mesh, num_elem, num_loc); wed.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc); // and display jacobian matrices int nb_pts = mat.GetNbPointsQuadratureBoundary(); for (int i = 0; i < nb_pts; i++) cout << "Jacobian matrix " << i << " = " << mat.GetPointQuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointDofBoundary
Syntax
| const MatrixN_N& GetPointDofBoundary(int i) const |
This method returns the jacobian matrix associated with the i-th dof point of a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for dof points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemDof(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElemDof(s, pts, mat, mesh, num_elem); // and quadrature points of the boundary int num_loc = 2; wed.FjElemSurfaceDof(s, pts, mesh, num_elem, num_loc); wed.DFjElemSurfaceDof(s, pts, mat, mesh, num_elem, num_loc); // and display jacobian matrices int nb_pts = mat.GetNbPointsDofBoundary(); for (int i = 0; i < nb_pts; i++) cout << "Jacobian matrix " << i << " = " << mat.GetPointDofBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetNormaleQuadratureBoundary
Syntax
| const R_N& GetNormaleQuadratureBoundary(int i) const |
This method returns the outgoing normale associated with the i-th quadrature point of a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // and quadrature points/normale of the boundary int num_loc = 2; wed.FjElemSurface(s, pts, mesh, num_elem, num_loc); wed.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc); // and display outgoing normales int nb_pts = mat.GetNbPointsQuadratureBoundary(); for (int i = 0; i < nb_pts; i++) cout << "Normale " << i << " = " << mat.GetNormaleQuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetPointNodalBoundary
Syntax
| const MatrixN_N& GetPointNodalBoundary( | int i) |
This method returns the jacobian matrix for the i-th nodal point of a boundary.
Example
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points int num_elem = 32; SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for nodal points SetMatrices<Dimension3> mat; pyr.DFjElemNodal(s, pts, mat, mesh, num_elem); // DFi on nodal points of boundary int num_loc = 1; mat.ComputeNodalBoundary(num_loc, pyr); // you can retrieve a jacobian matrix on a nodal point of the boundary int j = 2; // local number of the nodal point on the boundary Matrix3_3 dfj = mat.GetPointNodalBoundary(j);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetInversePointNodalBoundary
Syntax
| const MatrixN_N& GetInversePointNodalBoundary( | int i) |
This method returns the inverse of jacobian matrix for the i-th nodal point of a boundary.
Example
Mesh<Dimension3> mesh; MeshNumbering<Dimension3> mesh_num(mesh); PyramidClassical pyr; pyr.ConstructFiniteElement(3); pyr.SetMesh(mesh); // computing transformation Fi for nodal points int num_elem = 32; SetPoints<Dimension3> pts; VectR3 s; mesh.GetVerticesElement(num_elem, s); pyr.FjElemNodal(s, pts, mesh, num_elem); // computing jacobian matrices DFi for nodal points SetMatrices<Dimension3> mat; pyr.DFjElemNodal(s, pts, mat, mesh, num_elem); // DFi on nodal points of boundary int num_loc = 1; mat.ComputeNodalBoundary(num_loc, pyr); // you can retrieve a jacobian matrix on a nodal point of the boundary int j = 2; // local number of the nodal point on the boundary Matrix3_3 dfj = mat.GetPointNodalBoundary(j); // and you can retrieve the inverse as well (inverse has already been computed by ComputeNodalBoundary) Matrix3_3 inv_dfj = mat.GetInversePointNodalBoundary(j);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetDsQuadratureBoundary
Syntax
| const Real_wp& GetDsQuadratureBoundary(int i) const |
This method returns the surface element associated with the i-th quadrature point of a boundary.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi for quadrature points SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElemQuadrature(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem); // and quadrature points/normale of the boundary int num_loc = 2; wed.FjElemSurface(s, pts, mesh, num_elem, num_loc); wed.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc); // and display surface elements int nb_pts = mat.GetNbPointsQuadratureBoundary(); for (int i = 0; i < nb_pts; i++) cout << "Ds " << i << " = " << mat.GetDsQuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetK1QuadratureBoundary
Syntax
| const Real_wp& GetK1QuadratureBoundary(int i) const |
This method returns the first eigenvalue of the curvature tensor associated with the i-th quadrature point of a boundary.
Example
// finite element is constructed
WedgeClassical wed;
wed.ConstructFiniteElement(3);
wed.SetMesh(mesh);
// computing transformation Fi for quadrature points
SetPoints<Dimension3> pts;
VectR3 s; int num_elem = 40;
mesh.GetVerticesElement(num_elem, s);
wed.FjElemQuadrature(s, pts, mesh, num_elem);
// and jacobian matrices
SetMatrices<Dimension3> mat;
wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// and quadrature points/normale of the boundary
int num_loc = 2;
wed.FjElemSurface(s, pts, mesh, num_elem, num_loc);
wed.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc);
// and display eigenvalues of curvature tensor
int nb_pts = mat.GetNbPointsQuadratureBoundary();
for (int i = 0; i < nb_pts; i++)
cout << "Eigenvalues of C on point " << i << " = " << mat.GetK1QuadratureBoundary(i)
<< " and " << mat.GetK2QuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
GetK2QuadratureBoundary
Syntax
| const Real_wp& GetK2QuadratureBoundary(int i) const |
This method returns the first eigenvalue of the curvature tensor associated with the i-th quadrature point of a boundary.
Example
// finite element is constructed
WedgeClassical wed;
wed.ConstructFiniteElement(3);
wed.SetMesh(mesh);
// computing transformation Fi for quadrature points
SetPoints<Dimension3> pts;
VectR3 s; int num_elem = 40;
mesh.GetVerticesElement(num_elem, s);
wed.FjElemQuadrature(s, pts, mesh, num_elem);
// and jacobian matrices
SetMatrices<Dimension3> mat;
wed.DFjElemQuadrature(s, pts, mat, mesh, num_elem);
// and quadrature points/normale of the boundary
int num_loc = 2;
wed.FjElemSurface(s, pts, mesh, num_elem, num_loc);
wed.DFjElemSurface(s, pts, mat, mesh, num_elem, num_loc);
// and display eigenvalues of curvature tensor
int nb_pts = mat.GetNbPointsQuadratureBoundary();
for (int i = 0; i < nb_pts; i++)
cout << "Eigenvalues of C on point " << i << " = " << mat.GetK1QuadratureBoundary(i)
<< " and " << mat.GetK2QuadratureBoundary(i) << endl;
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
CopyNodalToQuadrature
Syntax
| void CopyNodalToQuadrature() |
This method copies jacobian matrices computed for nodal points to jacobian matrices associated with quadrature points. On regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsNodal(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointNodal(0, A0); mat.SetPointNodal(1, A1); // etc // if nodal points coincide with quadrature points, jacobian matrices are equal mat.CopyNodalToQuadrature();
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
CopyNodalToDof
Syntax
| void CopyNodalToDof() |
This method copies jacobian matrices computed for nodal points to jacobian matrices associated with dof points. On regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsNodal(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointNodal(0, A0); mat.SetPointNodal(1, A1); // etc // if nodal points coincide with dof points, jacobian matrices are equal mat.CopyNodalToDof();
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
CopyQuadratureToDof
Syntax
| void CopyQuadratureToDof() |
This method copies jacobian matrices computed for quadrature points to jacobian matrices associated with dof points. On regular use, this method should not be called.
Example
SetMatrices<Dimension2> mat; int N = 10; mat.ReallocatePointsQuadrature(N); // allocating the array // filling the array Matrix2_2 A0, A1; A0(0, 0) = 0.4; A0(0, 1) = 2.0; A0(1, 0) = -1.6; A0(1, 1) = 2.5; A1(0, 0) = 0.8; A1(0, 1) = 1.9; A1(1, 0) = -2.3; A1(1, 1) = 3.2; mat.SetPointQuadrature(0, A0); mat.SetPointQuadrature(1, A1); // etc // if quadrature points coincide with dof points, jacobian matrices are equal mat.CopyQuadratureToDof();
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReferenceInline.cxx
RotateNormale
Syntax
| void RotateNormale(Real_wp teta) |
This method rotates normales of an angle θ. The axis of rotation if the Ez axis, the new coordinates of the normales are given as:
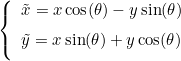
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElem(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElem(s, pts, mat, mesh, num_elem); // computing normales of a boundary int num_loc = 2; wed.FjSurfaceElem(s, pts, mesh, num_elem, num_loc); wed.DFjSurfaceElem(s, pts, mat, mesh, num_elem, num_loc); // you can rotate all normales mat.RotateNormale(pi_wp/3); // and retrieve a rotated normale R3 n = mat.GetNormaleQuadratureBoundary(1);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
InitSetPoints
Syntax
| void InitSetPoints(const SetPoints& pts) |
This method initializes the pointer storing an object SetPoints in the class, such that GetSetPoints will work correctly. On regular use, you do not need to call this method, because it is already done when DFjElem (and derivates such as DFjElemNodal) is called.
Example
SetPoints<Dimension2> pts; SetMatrices<Dimension2> mat; // if you want to store the adress of pts in the object mat : mat.InitSetPoints(pts); // then you can retrieve pts from the object mat const SetPoints<Dimension2> pts2 = mat.GetSetPoints(); // pts and pts2 should share the same address
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
GetSetPoints
Syntax
| const SetPoints& GetSetPoints() const |
This method returns the object SetPoints stored in the current object.
Example
// finite element is constructed WedgeClassical wed; wed.ConstructFiniteElement(3); wed.SetMesh(mesh); // computing transformation Fi SetPoints<Dimension3> pts; VectR3 s; int num_elem = 40; mesh.GetVerticesElement(num_elem, s); wed.FjElem(s, pts, mesh, num_elem); // and jacobian matrices SetMatrices<Dimension3> mat; wed.DFjElem(s, pts, mat, mesh, num_elem); // if you want to access to pts with only mat : const SetPoints<Dimension2> pts2 = mat.GetSetPoints(); // pts and pts2 are the same variable
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
non_linear_solver
Syntax
| static int non_linear_solver; |
This attribute stores the non-linear solver used to invert the transformation Fi. You can choose among the following non-linear solvers :
- NEWTON_SOLVER : Newton-Raphson solver
- MINPACK_SOLVER : Minpack solver
- LVM_SOLVER : Levenberg-Marquardt solver
If this attribute is not set, the default solver is NEWTON_SOLVER.
Example
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// setting the non-linear solver
FjInverseProblem<Dimension3>::non_linear_solver = FjInverseProblem<Dimension3>::LVM_SOLVER;
// initializing the solver
int num_elem = 21; R3 point(4.0, 11.0, -2.0); // global coordinates of point
FjInverseProblem<Dimension3> fj_inv(mesh, num_elem);
// computing pt_loc such that Fi(pt_loc) = point
bool pt_inside = fj_inv.Solve(point, pt_loc);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
nb_max_iterations
Syntax
| static int nb_max_iterations; |
This attribute stores the maximum number of iterations allowed for the non-linear solver. If this attribute is not set, the default maximum number of iterations is set to 50.
Example
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// setting the maximum number of iterations
FjInverseProblem<Dimension3>::nb_max_iterations = 10;
// initializing the solver
int num_elem = 21; R3 point(4.0, 11.0, -2.0); // global coordinates of point
FjInverseProblem<Dimension3> fj_inv(mesh, num_elem);
// computing pt_loc such that Fi(pt_loc) = point
bool pt_inside = fj_inv.Solve(point, pt_loc);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
threshold_newton
Syntax
| static Real_wp threshold_newton; |
This attribute stores the stopping criterion used by the non-linear solver. If this attribute is not set, the default value is 4*epsilon_machine where epsilon_machine is the machine precision (2e-16 in double precision).
Example
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// setting the maximum number of iterations
FjInverseProblem<Dimension3>::nb_max_iterations = 10;
// and stopping criterion
FjInverseProblem<Dimension3>::threshold_newton = 1e-14;
// initializing the solver
int num_elem = 21; R3 point(4.0, 11.0, -2.0); // global coordinates of point
FjInverseProblem<Dimension3> fj_inv(mesh, num_elem);
// computing pt_loc such that Fi(pt_loc) = point
bool pt_inside = fj_inv.Solve(point, pt_loc);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
coef_safety_solver
Syntax
| static Real_wp coef_safety_solver; |
This attribute stores the safety coefficient used to determine if the solution found is outside the reference element. A larger coefficient leads to admit more solutions that are very close the reference element. A smaller coefficient can lead to exclude some solutions that are computed outside the reference element because of round-off errors.
Example
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// setting the maximum number of iterations
FjInverseProblem<Dimension3>::nb_max_iterations = 10;
// and stopping criterion
FjInverseProblem<Dimension3>::threshold_newton = 1e-14;
// safety coefficient to admit more solutions
FjInverseProblem<Dimension3>::coef_safety_solver = 100;
// initializing the solver
int num_elem = 21; R3 point(4.0, 11.0, -2.0); // global coordinates of point
FjInverseProblem<Dimension3> fj_inv(mesh, num_elem);
// computing pt_loc such that Fi(pt_loc) = point
bool pt_inside = fj_inv.Solve(point, pt_loc);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
GetVertices
Syntax
| VectR_N& GetVertices() |
This method gives access to the list of vertices of the element that have been extracted in the constructor.
Example
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// initializing the solver
int num_elem = 21; R3 point(4.0, 11.0, -2.0); // global coordinates of point
FjInverseProblem<Dimension3> fj_inv(mesh, num_elem);
// you can retrieve the list of vertices extracted in the constructor :
VectR3& s = fj_inv.GetVertices();
// computing pt_loc such that Fi(pt_loc) = point
bool pt_inside = fj_inv.Solve(point, pt_loc);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
GetSetPoints
Syntax
| SetPoints& GetSetPoints() |
This method gives access to the list of points of the element that have been computed in the constructor. These points are not computed if the element is affine (in such case, the inversion of transformation Fi is straightforward).
Example
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// initializing the solver
int num_elem = 21; R3 point(4.0, 11.0, -2.0); // global coordinates of point
FjInverseProblem<Dimension3> fj_inv(mesh, num_elem);
// you can retrieve the list of points of the element
SetPoints<Dimension3>& pts = fj_inv.GetSetPoints();
// computing pt_loc such that Fi(pt_loc) = point
bool pt_inside = fj_inv.Solve(point, pt_loc);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
Solve
Syntax
| bool Solve(const R_N& pt_glob, const R_N& pt_loc, int print_level=0) |
This method computes the solution pt_loc of Fi(pt_loc) = pt_glob. It returns true if the element is inside the reference element.
Parameters
- pt_glob (in)
- coordinates of the point in the real element
- pt_loc (out)
- coordinates of the point in the reference element
- print_level (optional)
- if greater than 0, the residual is printed
Example
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
// initializing the solver
int num_elem = 21; R3 point(4.0, 11.0, -2.0); // global coordinates of point
FjInverseProblem<Dimension3> fj_inv(mesh, num_elem);
// computing pt_loc such that Fi(pt_loc) = point
bool pt_inside = fj_inv.Solve(point, pt_loc);
Location :
FiniteElement/PointsReference.hxx FiniteElement/PointsReference.cxx
SetIdentity
Syntax
| void SetIdentity(const IVect& col, const IVect& row, int n) |
This method sets the projector as a permutation matrix :
Prow(i), col(i) = 1
Parameters
- col (in)
- column numbers
- row (in)
- row numbers
- n (in)
- total number of rows
Example
DenseProjector<Dimension2> proj; // rows and colums such that P(i, j) is equal to 1 // for other indexes P(k, l) is equal to 0 IVect row(3), col(3); row(0) = 1; row(1) = 2; row(2) = 0; col(0) = 0; col(1) = 1; col(2) = 2; proj.SetIdentity(col, row, 3);
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
Project
Syntax
| void Project(const Vector& u, Vector& v) const |
This method computes v = P u where P is the projection operator, usually given as
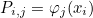
where φj are shape functions and xi interpolation points.
Parameters
- u (in)
- components of the field on shape functions
- v (out)
- values of the field on interpolation points
Example
// case of a tensorized projector (e.g. with quadrilaterals) QuadrangleGeomReference quad; quad.ConstructFiniteElement(4); // definition of points where we want to interpolate the solution VectR2 pts_interp(10); pts_interp(0).Init(0.4, 0.7); pts_interp(1).Init(0.2, 0.9); // etc // computation of operator P TensorizedProjector<Dimension2> proj; proj.Init(quad, pts_interp); // random field VectReal_wp u(quad.GetNbPointsNodalElt()), v; u.FillRand(); // computation of v = P u to obtain the solution on interpolation points proj.Project(u, v); // you can also project vectorial fields : VectR3 E(quad.GetNbPointsNodalElt()), Einterp; E(0).Init(0.9, 1.2, -0.5); // etc proj.Project(E, Einterp);
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
TransposeProject
Syntax
| void TransposeProject(const Vector& v, Vector& u) const |
This method computes u = PT v where P is the projection operator, usually given as
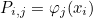
where φj are shape functions and xi interpolation points.
Example
// case of a tensorized projector (e.g. with quadrilaterals) QuadrangleGeomReference quad; quad.ConstructFiniteElement(4); // definition of points where we want to interpolate the solution VectR2 pts_interp(10); pts_interp(0).Init(0.4, 0.7); pts_interp(1).Init(0.2, 0.9); // etc // computation of operator P TensorizedProjector<Dimension2> proj; proj.Init(quad, pts_interp); // random field VectReal_wp u(quad.GetNbPointsNodalElt()), v; u.FillRand(); // computation of v = P u to obtain the solution on interpolation points proj.Project(u, v); // application of transpose operator u = P^T v proj.TransposeProject(v, u); // you can also transpose project vectorial fields : VectR3 vE(pts_interp.GetM()), uE; vE(0).Init(0.9, 1.2, -0.5); // etc proj.TransposeProject(vE, uE);
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
GetMemorySize
Syntax
| size_t GetMemorySize() const |
This method returns the memory used by the object in bytes.
Example
// case of a tensorized projector (e.g. with quadrilaterals) QuadrangleGeomReference quad; quad.ConstructFiniteElement(4); // definition of points where we want to interpolate the solution VectR2 pts_interp(10); pts_interp(0).Init(0.4, 0.7); pts_interp(1).Init(0.2, 0.9); // etc // computation of operator P TensorizedProjector<Dimension2> proj; proj.Init(quad, pts_interp); // memory used to store proj ? size_t mem = proj.GetMemorySize();
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
Init
Syntax
| void Init(const ElementGeomReference& elt, const VectR_N& pts_elt) const |
| size_t Init(const ElementGeomReference& elt, const VectReal_wp& pts1d, const VectR_N& pts_elt) const |
This method computes the projection operator P usually given as
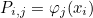
where φj are shape functions and xi interpolation points. For the class TensorizedProjector, the matrix is not explicitely stored. In this class, sparse matrices are constructed, such that P is a product of sparse matrices. The matrix-vector product with P can be performed by the method Project (method TransposeProject) for the product with the transpose of P). In the second syntax, you can provide the 1-D interpolation points (useful for TensorizedProjector).
Parameters
- elt (in)
- geometric finite element
- pts1d (optional)
- 1-D interpolation points
- pts_elt (in)
- interpolation points
Example
// case of a tensorized projector (e.g. with quadrilaterals) QuadrangleGeomReference quad; quad.ConstructFiniteElement(4); // definition of points where we want to interpolate the solution VectR2 pts_interp(10); pts_interp(0).Init(0.4, 0.7); pts_interp(1).Init(0.2, 0.9); // etc // computation of operator P TensorizedProjector<Dimension2> proj; proj.Init(quad, pts_interp);
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
ProjectScalar
Syntax
| void ProjectScalar(const Vector& u, Vector& v) const |
This method computes v = P u where P is the projection operator, usually given as
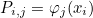
where φj are shape functions and xi interpolation points. This method is virtual such that if you want to define a new class that derives from FiniteElementProjector, this method can be overloaded to define the matrix-vector product with P.
Parameters
- u (in)
- components of the field on shape functions
- v (out)
- values of the field on interpolation points
Example
// case of a tensorized projector (e.g. with quadrilaterals) QuadrangleGeomReference quad; quad.ConstructFiniteElement(4); // definition of points where we want to interpolate the solution VectR2 pts_interp(10); pts_interp(0).Init(0.4, 0.7); pts_interp(1).Init(0.2, 0.9); // etc // computation of operator P TensorizedProjector<Dimension2> proj; proj.Init(quad, pts_interp); // random field VectReal_wp u(quad.GetNbPointsNodalElt()), v; u.FillRand(); // computation of v = P u to obtain the solution on interpolation points proj.ProjectScalar(u, v);
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
TransposeProjectScalar
Syntax
| void TransposeProjectScalar(const Vector& v, Vector& u) const |
This method computes u = PT v where P is the projection operator, usually given as
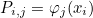
where φj are shape functions and xi interpolation points. This method is virtual such that if you want to define a new class that derives from FiniteElementProjector, this method can be overloaded to define the matrix-vector product with PT.
Example
// case of a tensorized projector (e.g. with quadrilaterals) QuadrangleGeomReference quad; quad.ConstructFiniteElement(4); // definition of points where we want to interpolate the solution VectR2 pts_interp(10); pts_interp(0).Init(0.4, 0.7); pts_interp(1).Init(0.2, 0.9); // etc // computation of operator P TensorizedProjector<Dimension2> proj; proj.Init(quad, pts_interp); // random field VectReal_wp u(quad.GetNbPointsNodalElt()), v; u.FillRand(); // computation of v = P u to obtain the solution on interpolation points proj.ProjectScalar(u, v); // application of transpose operator u = P^T v proj.TransposeProjectScalar(v, u);
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
InitProjection
Syntax
| void InitProjection(const Vector<ElementGeomReference*>& liste_elt, const Vector<VectR_N>& liste_pts) const |
| void InitProjection(const Vector<ElementGeomReference*>& liste_elt, const VectReal_wp& pts1d, const Vector<VectR_N>& liste_pts) const |
This method computes the projection operators P usually given as
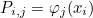
where φj are shape functions and xi interpolation points. It computes the operators for the elements present in the first argument. The elements can be a mix of tetrahedra/pyramids/prisms/hexahedra (triangles/quadrilaterals in 2-D). In the second syntax, you can provide the 1-D interpolation points.
Parameters
- liste_elt (in)
- list of geometric finite elements (of the same order)
- pts1d (optional)
- 1-D interpolation points
- liste_pts (in)
- interpolation points for the different elements
Example
// starting with a 3-D mesh
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
Vector<VectR3> pts_3d(4);
// points for the unit tetrahedron
pts_3d(0).Reallocate(5);
pts_3d(0)(0).Init(0.2, 0.2, 0.1); // etc
// for the symmetric pyramid
pts_3d(1).Reallocate(10);
pts_3d(1)(0).Init(-0.3, 0.4, 0.2); // etc
// pts_3d(2) for the prism and pts_3d(3) for the pyramid
// in 2-D, pts(0) for the unit triangle and pts(1) for the unit square
// computing the projection for all elements (tet, pyramids, hex, prisms)
FiniteElementInterpolator liste_proj;
liste_proj.InitProjection(mesh.GetReferenceElement(), pts_3d);
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
ProjectScalar
Syntax
| void ProjectScalar(const Vector& u, Vector& v, int type_elt) const |
This method computes v = P u where P is the projection operator, usually given as
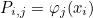
where φj are shape functions and xi interpolation points.
Parameters
- u (in)
- components of the field on shape functions
- v (out)
- values of the field on interpolation points
- type_elt (in)
- type of element (as returned by GetHybridType())
Example
// starting with a 3-D mesh
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
Vector<VectR3> pts_3d(4);
// points for the unit tetrahedron
pts_3d(0).Reallocate(5);
pts_3d(0)(0).Init(0.2, 0.2, 0.1); // etc
// for the symmetric pyramid
pts_3d(1).Reallocate(10);
pts_3d(1)(0).Init(-0.3, 0.4, 0.2); // etc
// pts_3d(2) for the prism and pts_3d(3) for the pyramid
// in 2-D, pts(0) for the unit triangle and pts(1) for the unit square
// computing the projection for all elements (tet, pyramids, hex, prisms)
FiniteElementInterpolator liste_proj;
liste_proj.InitProjection(mesh.GetReferenceElement(), pts_3d);
// projection for an element of the mesh:
int num_elem = 12;
VectReal_wp u(mesh.GetNbPointsNodalElt(num_elem));
u.FillRand();
VectReal_wp u_interp;
liste_proj.ProjectScalar(u, u_interp, mesh.Element(num_elem).GetHybridType());
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
TransposeProjectScalar
Syntax
| void TransposeProjectScalar(const Vector& u, Vector& v, int type_elt) const |
This method computes v = PT u where P is the projection operator, usually given as
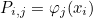
where φj are shape functions and xi interpolation points.
Parameters
- u (in)
- input vector
- v (out)
- result vector
- type_elt (in)
- type of element (as returned by GetHybridType())
Example
// starting with a 3-D mesh
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
Vector<VectR3> pts_3d(4);
// points for the unit tetrahedron
pts_3d(0).Reallocate(5);
pts_3d(0)(0).Init(0.2, 0.2, 0.1); // etc
// for the symmetric pyramid
pts_3d(1).Reallocate(10);
pts_3d(1)(0).Init(-0.3, 0.4, 0.2); // etc
// pts_3d(2) for the prism and pts_3d(3) for the pyramid
// in 2-D, pts(0) for the unit triangle and pts(1) for the unit square
// computing the projection for all elements (tet, pyramids, hex, prisms)
FiniteElementInterpolator liste_proj;
liste_proj.InitProjection(mesh.GetReferenceElement(), pts_3d);
// projection for an element of the mesh:
int num_elem = 12;
VectReal_wp u(mesh.GetNbPointsNodalElt(num_elem));
u.FillRand();
VectReal_wp u_interp;
liste_proj.ProjectScalar(u, u_interp, mesh.Element(num_elem).GetHybridType());
// and transpose operator (u = P^T u_interp)
liste_proj.TransposeProjectScalar(u_interp, u, mesh.Element(num_elem).GetHybridType());
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
Project
Syntax
| void Project(const Vector& u, Vector& v, int type_elt) const |
This method computes v = P u where P is the projection operator, usually given as
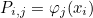
where φj are shape functions and xi interpolation points. The field can be scalar or vectorial.
Parameters
- u (in)
- components of the field on shape functions
- v (out)
- values of the field on interpolation points
- type_elt (in)
- type of element (as returned by GetHybridType())
Example
// starting with a 3-D mesh
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
Vector<VectR3> pts_3d(4);
// points for the unit tetrahedron
pts_3d(0).Reallocate(5);
pts_3d(0)(0).Init(0.2, 0.2, 0.1); // etc
// for the symmetric pyramid
pts_3d(1).Reallocate(10);
pts_3d(1)(0).Init(-0.3, 0.4, 0.2); // etc
// pts_3d(2) for the prism and pts_3d(3) for the pyramid
// in 2-D, pts(0) for the unit triangle and pts(1) for the unit square
// computing the projection for all elements (tet, pyramids, hex, prisms)
FiniteElementInterpolator liste_proj;
liste_proj.InitProjection(mesh.GetReferenceElement(), pts_3d);
// projection for an element of the mesh (we take a vectorial field)
int num_elem = 12;
VectR3 u(mesh.GetNbPointsNodalElt(num_elem));
u(0).Init(0.2, 0.5, 1.1); // etc
VectR3 u_interp;
liste_proj.Project(u, u_interp, mesh.Element(num_elem).GetHybridType());
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
TransposeProject
Syntax
| void TransposeProject(const Vector& u, Vector& v, int type_elt) const |
This method computes v = PT u where P is the projection operator, usually given as
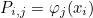
where φj are shape functions and xi interpolation points. The fields u and v can be scalar fields or vectorial fields.
Parameters
- u (in)
- input vector
- v (out)
- result vector
- type_elt (in)
- type of element (as returned by GetHybridType())
Example
// starting with a 3-D mesh
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
Vector<VectR3> pts_3d(4);
// points for the unit tetrahedron
pts_3d(0).Reallocate(5);
pts_3d(0)(0).Init(0.2, 0.2, 0.1); // etc
// for the symmetric pyramid
pts_3d(1).Reallocate(10);
pts_3d(1)(0).Init(-0.3, 0.4, 0.2); // etc
// pts_3d(2) for the prism and pts_3d(3) for the pyramid
// in 2-D, pts(0) for the unit triangle and pts(1) for the unit square
// computing the projection for all elements (tet, pyramids, hex, prisms)
FiniteElementInterpolator liste_proj;
liste_proj.InitProjection(mesh.GetReferenceElement(), pts_3d);
// projection for an element of the mesh (we take a vectorial field)
int num_elem = 12;
VectR3 u(mesh.GetNbPointsNodalElt(num_elem));
u(0).Init(2.1, -1.6, 3.2); // etc
VectR3 u_interp;
liste_proj.Project(u, u_interp, mesh.Element(num_elem).GetHybridType());
// and transpose operator (u = P^T u_interp)
liste_proj.TransposeProject(u_interp, u, mesh.Element(num_elem).GetHybridType());
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
ComputeLocalProlongation
Syntax
| void ComputeLocalProlongation( | const Vector<ElementReference>& elt_fine, int rf, |
| const Vector<ElementReference>& elt_coarse, int rc, | |
| TinyVector<Matrix<Real_wp>, 4>& ProlongationMatrix) |
This method computes the local prolongation operator (as detailed in ComputeLocalProlongation between a coarse finite element and a fine element.
Parameters
- elt_fine (in)
- list of fine elements
- rf (in)
- fine order
- elt_coarse (in)
- list of coarse elements
- rc (in)
- coarse order
- ProlongationMatrix (out)
- prolongation matrices (if stored)
Example
// coarse finite elements TriangleClassical tri; QuadrangleGauss quad; tri.ConstructFiniteElement(2); quad.ConstructFiniteElement(2); // fine finite elements TriangleClassical tri_f; QuadrangleGauss quad_f; tri_f.ConstructFiniteElement(4); quad_f.ConstructFiniteElement(4); // list of elements (usually associated with elements of the mesh) Vector<const ElementReference<Dimension2, 1>* > elt_fine(6); Vector<const ElementReference<Dimension2, 1>* > elt_coarse(6); elt_fine(0) = &tri_f; elt_fine(1) = &quad_f; elt_fine(2) = &quad_f; elt_fine(3) = &tri_f; elt_fine(4) = &tri_f; elt_fine(5) = &quad_f; elt_coarse(0) = &tri; elt_coarse(1) = &quad; elt_coarse(2) = &quad; elt_coarse(3) = &tri; elt_coarse(4) = &tri; elt_coarse(5) = &quad; // computation of prolongation operator FiniteElementInterpolator proj; TinyVector<Matrix<Real_wp>, 4> ProlongationMatrix; proj.ComputeLocalProlongation(elt_fine, 4, elt_coarse, 2, ProlongationMatrix); // to prolongate a field on the coarse mesh to the fine mesh => use Project VectReal_wp u_coarse(tri.GetNbDof()), u_fine(tri_f.GetNbDof()); proj.Project(u_coarse, u_fine, 0); // 0 = triangle, 1 = quad // for the restriction, use TransposeProject proj.TransposeProject(u_fine, u_coarse, 0); // 0 = triangle, 1 = quad
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx
ComputeLocalProlongationLowOrder
Syntax
| void ComputeLocalProlongationLowOrder( | const Vector<ElementReference>& elt_fine, int rf, |
| const Vector<ElementReference>& elt_coarse, int rc, | |
| TinyVector<Matrix<Real_wp>, 4>& ProlongationMatrix) |
This method computes the local prolongation operator (as detailed in ComputeLocalProlongationLowOrder between a coarse finite element and a fine element by using first order basis functions.
Parameters
- elt_fine (in)
- list of fine elements
- rf (in)
- fine order
- elt_coarse (in)
- list of coarse elements
- rc (in)
- coarse order
- ProlongationMatrix (out)
- prolongation matrices (if stored)
Example
// coarse finite elements TriangleClassical tri; QuadrangleGauss quad; tri.ConstructFiniteElement(2); quad.ConstructFiniteElement(2); // fine finite elements TriangleClassical tri_f; QuadrangleGauss quad_f; tri_f.ConstructFiniteElement(4); quad_f.ConstructFiniteElement(4); // list of elements (usually associated with elements of the mesh) Vector<const ElementReference<Dimension2, 1>* > elt_fine(6); Vector<const ElementReference<Dimension2, 1>* > elt_coarse(6); elt_fine(0) = &tri_f; elt_fine(1) = &quad_f; elt_fine(2) = &quad_f; elt_fine(3) = &tri_f; elt_fine(4) = &tri_f; elt_fine(5) = &quad_f; elt_coarse(0) = &tri; elt_coarse(1) = &quad; elt_coarse(2) = &quad; elt_coarse(3) = &tri; elt_coarse(4) = &tri; elt_coarse(5) = &quad; // computation of prolongation operator (with low order basis functions) FiniteElementInterpolator proj; TinyVector<Matrix<Real_wp>, 4> ProlongationMatrix; proj.ComputeLocalProlongationLowOrder(elt_fine, 4, elt_coarse, 2, ProlongationMatrix); // to prolongate a field on the coarse mesh to the fine mesh => use Project VectReal_wp u_coarse(tri.GetNbDof()), u_fine(tri_f.GetNbDof()); proj.Project(u_coarse, u_fine, 0); // 0 = triangle, 1 = quad // for the restriction, use TransposeProject proj.TransposeProject(u_fine, u_coarse, 0); // 0 = triangle, 1 = quad
Location :
FiniteElement/ProjectionOperator.hxx FiniteElement/ProjectionOperator.cxx