Tetrahedral finite elements spaces
In this page, we detail the different tetrahedral finite elements currently implemented in Montjoie. The reference element is the unit tetrahedron, look at the figure below for the conventions used
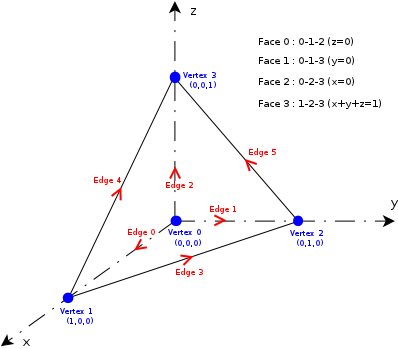
If you want to implement a new tetrahedral element, you have to derive the class TetrahedronReference. This class is the base class for all tetrahedral elements implemented in Montjoie. It depends on the type of element (1: scalar finite element, 2: edge elements, 3: facet elements).
// for a new tetrahedral finite element (1 : scalar)
class MyFiniteElement : public TetrahedronReference<1>
{
public :
// number of dofs on each edge, triangle, tetrahedron, etc ?
void ConstructNumberMap(NumberMap& map, int dg) const;
// main method used to construct the finite element object
// r : order of approximation for basis functions
// rgeom : order of approximation for geometry (shape functions)
// rquad : order of quadrature
// if rgeom is equal to 0 (and similarly rquad equal to 0)
// we are considering that rgeom = r, and rquad = r
// if type_quad is equal to -1, we use the default quadrature
// formulas (probably Gauss formulas)
// rsurf_tri, rsurf_quad : orders for boundary integrals
// type_surf_tri, type_surf_quad : type of integration for triangles and quadrangles
void ConstructFiniteElement(int r, int rgeom = 0, int rquad = 0, int type_quad = -1,
int rsurf_tri = 0, int rsurf_quad = 0, int type_surf_tri = -1,
int type_surf_quad = -1, int gauss_z = -1);
// computation of phi_i(x) for a given point x
// the values phi_i(x) have to be placed in the array phi
void ComputeValuesPhiRef(const R3& x, VectReal_wp& phi) const;
// computation of \nabla phi_i(x) for a given point x
void ComputeGradientPhiRef(const R3& x, VectR3& grad_phi) const;
};
TetrahedronGeomReference
The class TetrahedronGeomReference implements shape functions methods for tetrahedron elements. These shape functions are computed as a linear combination of orthogonal polynomials :
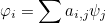
where ψj form an orthogonal basis of polynomials of degree r. We choose the following basis:
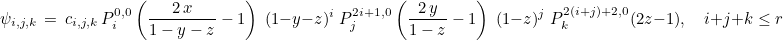
where Piα, β are Jacobi polynomials orthogonal with respect to weight (1-x)α(1+x)β. The coefficients ci, j, k are chosen such that the polynomials are actually orthonormal :
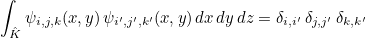
The coefficients ai, j are computed by inverting a Vandermonde's matrix:
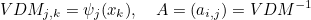
Most of the methods of this class come from the parent class ElementGeomReference. Below, we detail the methods and attributes specific to the class TetrahedronGeomReference.
| GetNbPointsNodalInside | returns the number of nodal points inside the tetrahedron. |
| type_interpolation_nodal | choice of nodal points |
| GetLegendrePolynomial | returns Legendre polynomials stored in the class |
| GetInvWeightPolynomial | returns the coefficients ci, j, k applied to obtain orthonormal polynomials ψj |
| GetCoefLegendre | returns the coefficients used to normalize Legendre polynomialsj |
| GetNumOrtho3D | returns the orthogonal polynomial number k from the tuple (i, j, k) |
| GetOddJacobiPolynomial | returns the odd Jacobi polynomials
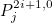
|
| GetEvenJacobiPolynomial | returns the even Jacobi polynomials
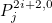
|
| GetCoefOddJacobi | returns the coefficients used to normalize odd Jacobi polynomialsj |
| GetCoefEvenJacobi | returns the coefficients used to normalize even Jacobi polynomialsj |
| ConstructRegularPoints | computes nodal points regularly spaced |
| ConstructLobattoPoints | computes nodal points with a small Lebesgue constant |
| ComputeOrthogonalFunctions | constructs orthogonal functions only |
| ComputeValuesPhiOrthoRef | Evaluates orthonormal polynomials at a given point |
| ComputeGradientPhiOrthoRef | Evaluates the gradient of orthonormal polynomials at a given point |
TetrahedronReference
The class TetrahedronReference is the base class for all tetrahedral finite elements. Methods and attributes come from the parent class ElementReference.
TetrahedronClassical
This class implements a scalar finite element with interpolatory basis functions. It can be used to discretize H1. The finite element space considered consists of polynomials of total degree less or equal to r :
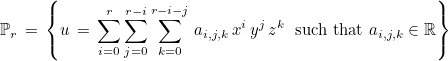
Similarly to TetrahedronGeomReference, the following orthogonal basis is used :
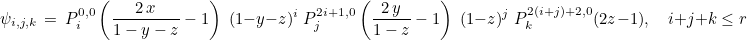
where
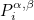 are Jacobi polynomials on [-1,1] orthogonal with respect to the weight
are Jacobi polynomials on [-1,1] orthogonal with respect to the weight
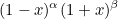 The basis functions are based on interpolation points xj and computed by
inverting the Vandermonde matrix :
The basis functions are based on interpolation points xj and computed by
inverting the Vandermonde matrix :
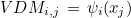
The basis functions are then equal to
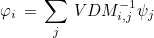
The interpolation points xj are chosen as points coming from an electrostatic problem as described by Hestaven (1998). These points include Gauss-Lobatto points along each edge and the same nodal points as for TriangleGeomReference on each triangular face. The used quadrature formulas are symmetric (QUADRATURE_GAUSS) for volume integrals and boundary integrals. The class TetrahedronClassical allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidClassical, WedgeClassical, HexahedronGauss. The class TetrahedronClassical is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_CLASSICAL or TypeElement = TETRAHEDRON_LOBATTO or TypeElement = HEXAHEDRON_LOBATTO in the datafile.
TetrahedronDgOrtho
This class implements a scalar finite element with orthogonal basis functions. It can be used to discretize L2 with discontinuous Galerkin formulations. The finite element space is the same as for TetrahedronClassical (polynomials of degree less or equal to r). The basis functions used for this class are the orthogonal functions
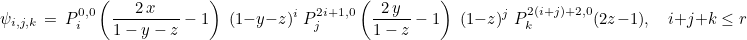
Because of tensorized structure, fast computations are obtained for a large order of approximation. The quadrature rules are obtained with Duffy transformation (QUADRATURE_TENSOR). Boundary integrals are evaluated with classical rules (not tensorized). This class allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidDgOrtho, WedgeDgOrtho, HexahedronDgGauss. The class TetrahedronClassical is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_DG_ORTHO or TypeElement = TETRAHEDRON_DG_LEGENDRE in the datafile.
TetrahedronHierarchic
The basis functions for this class are hierarchical, allowing the use of a variable order in a mesh. The basis functions are equal to :

The tensor structure of this basis is exploited to obtain faster computations for large values of r. Tensorized quadrature rules are therefore used (QUADRATURE_TENSOR) for volume integrals whereas symmetric rules are used for boundary integrals. The class TetrahedronHierarchic allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidHierarchic, WedgeHierarchic, HexahedronHierarchic. The class TetrahedronClassical is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_HIERARCHIC.
TetrahedronHcurlFirstFamily
This class implements interpolatory basis functions for edge elements of Nedelec's first family. It can be used to discretize H(curl) space. The finite element space considered here is equal to
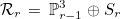
where
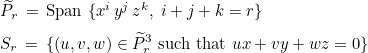
This space is generated with nearly orthogonal basis functions ψi :
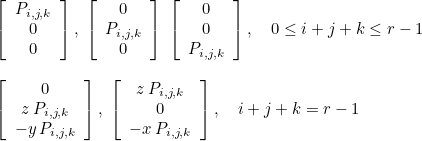
where
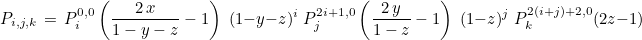
Each degree of freedom is associated with a position x and a tangent t. The Vandermonde matrix is then equal to
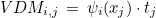
The interpolatory basis functions are then equal to
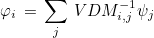
For each triangular face the nodal points and tangents are chosen to coincide with those of the class TriangleHcurlFirstFamily (e.g. Gauss points along edges). For the degrees of freedom inside the element, nodal points are chosen as interior points of the nodal tetrahedron (TetrahedronClassical) of order r+1. The class TetrahedronHcurlFirstFamily allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidHcurlFirstFamily, WedgeHcurlFirstFamily, HexahedronHcurlFirstFamily. The class TetrahedronHcurlFirstFamily is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_FIRST_FAMILY or TypeElement = HEXAHEDRON_FIRST_FAMILY.
TetrahedronHcurlOptimalFirstFamily
This finite element class is similar to the class TetrahedronHcurlFirstFamily. The only difference is that nodal points along edges are chosen as interior Gauss-Lobatto points (instead of Gauss points), so that this element is compatible with pyramids, prisms and hexahedra. It allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidHcurlOptimalFirstFamily, WedgeHcurlOptimalFirstFamily, HexahedronHcurlOptimalFirstFamily. The class TetrahedronHcurlOptimalFirstFamily is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_OPTIMAL_FIRST_FAMILY.
TetrahedronHcurlLobatto
This finite element class implements interpolatory basis functions for
tetrahedral edge elements of Nedelec's second family. It can be used to discretize H(curl) space.
The finite element space is
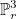 . Interpolation points
are the same as for TetrahedronClassical. Numerical computations
cannot be conducted over hybrid meshes, however you can use purely
tetrahedral or purely hexahedral meshes, the corresponding class
for hexahedra is the
class HexahedronHcurlLobatto. It
should be noticed that Nedelec's second family produces spurious
modes for hexahedral elements.
. Interpolation points
are the same as for TetrahedronClassical. Numerical computations
cannot be conducted over hybrid meshes, however you can use purely
tetrahedral or purely hexahedral meshes, the corresponding class
for hexahedra is the
class HexahedronHcurlLobatto. It
should be noticed that Nedelec's second family produces spurious
modes for hexahedral elements.
TetrahedronHcurlOptimalHpFirstFamily
This class implements hierarchical basis functions for edge tetrahedral edge elements of Nedelec's first family. The finite element space is the same as for TetrahedronHcurlFirstFamily. It can be used to discretize H(curl) space. The finite element space is the same as for TetrahedronHcurlFirstFamily. By using hierarchical functions, a variable order can be set for each element of the mesh. The basis functions are equal to :

This class allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidHcurlHpFirstFamily, WedgeHcurlHpFirstFamily, HexahedronHcurlHpFirstFamily. The class TetrahedronHcurlOptimalHpFirstFamily is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_OPTIMAL_HP_FIRST_FAMILY or TypeElement = TETRAHEDRON_HP_FIRST_FAMILY.
TetrahedronHdivFirstFamily
This class implements interpolatory basis functions for facet elements of Nedelec's first family. It can be used to discretize H(div) space. The finite element space considered here is equal to
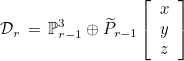
where
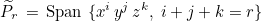
This space is generated with nearly orthogonal basis functions ψi :
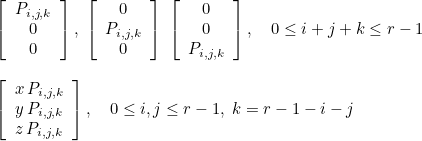
where
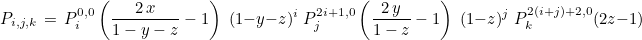
Each degree of freedom is associated with a position x and a tangent t. The Vandermonde matrix is then equal to
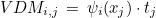
The interpolatory basis functions are then equal to
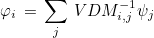
For each triangular face the interpolation points and tangents are chosen to coincide with interior points of the class TriangleClassical of order r+2. For the degrees of freedom inside the element, interpolation points are chosen as interior points of the tetrahedron (TetrahedronClassical) of order r+2. The class TetrahedronHdivFirstFamily allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidHdivFirstFamily, WedgeHdivFirstFamily, HexahedronHdivFirstFamily. The class TetrahedronHdivFirstFamily is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_FIRST_FAMILY or TypeElement = HEXAHEDRON_FIRST_FAMILY.
TetrahedronHdivOptimalFirstFamily
This finite element class is equivalent to the class TetrahedronHdivFirstFamily. It allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidHdivOptimalFirstFamily, WedgeHdivOptimalFirstFamily, HexahedronHdivOptimalFirstFamily. The class TetrahedronHdivOptimalFirstFamily is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_OPTIMAL_FIRST_FAMILY.
TetrahedronHdivOptimalHpFirstFamily
This class implements hierarchical basis functions for tetrahedral facet elements of Nedelec's first family. It can be used to discretize H(div) space. The finite element space is the same as for TetrahedronHdivFirstFamily. By using hierarchical functions, a variable order can be set for each element of the mesh. The basis functions are equal to :
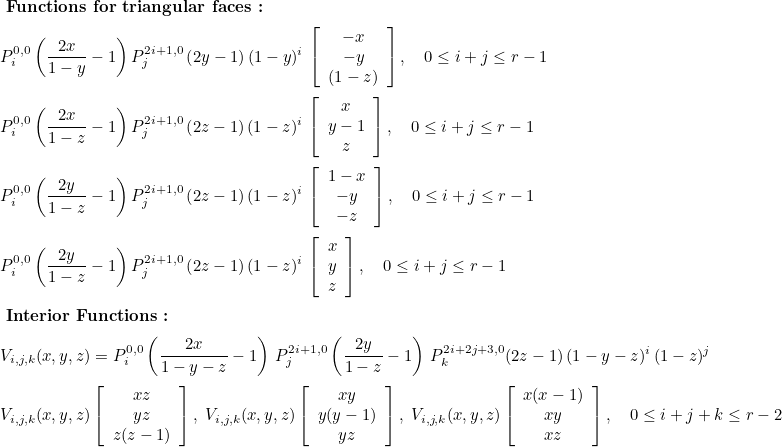
This class allows numerical computations over hybrid meshes, the corresponding classes for pyramids, prisms and hexahedra are PyramidHdivHpFirstFamily, WedgeHdivHpFirstFamily, HexahedronHdivHpFirstFamily. The class TetrahedronHdivOptimalHpFirstFamily is the class used for tetrahedra if you have TypeElement = TETRAHEDRON_OPTIMAL_HP_FIRST_FAMILY or TypeElement = TETRAHEDRON_HP_FIRST_FAMILY.
GetNbPointsNodalInside
Syntax
| int GetNbPointsNodalInside() const |
This method returns the number of nodal points strictly inside the unit tetrahedron. It should be equal to (r-1)(r-2)(r-3)/6 where r is the polynomial degree.
Example :
int r = 4; // polynomial degree TetrahedronGeomReference tet; tet.ConstructFiniteElement(r); // number of nodal points inside the tetrahedron ? int nb_nodes_inside = tet.GetNbPointsNodalInside(); // should give 1 here
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
type_interpolation_nodal
Syntax
| int type_interpolation_nodal |
This public attribute stores the family of nodal points to use when ConstructFiniteElement is called. You can choose between the following values:
- LOBATTO_BASIS : the nodal points will correspond to Hesthaven's points based on an analogy with electrostatic's equilibrium
- REGULAR_BASIS: the nodal are regularly spaced. This choice leads to a large Lebesgue constant, it implies a Runge phenomenon if nodal points are used for interpolation
The default value is LOBATTO_BASIS. The last value REGULAR_BASIS should be used cautiously for moderate polynomial degree.
Example :
int r = 4; // polynomial degree TetrahedronGeomReference tet; tet.type_interpolation_nodal = tri.REGULAR_BASIS; tet.ConstructFiniteElement(r);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx
GetLegendrePolynomial
Syntax
| const Matrix<Real_wp>& GetLegendrePolynomial() const |
This method returns the Legendre polynomials stored in the class (used for orthogonal polynomials ψj). These Legendre polynomials have been constructed with GetJacobiPolynomial. You can call EvaluateJacobiPolynomial to evaluate these polynomials.
Example :
int r = 4; // polynomial degree TetrahedronGeomReference tet; tet.ConstructFiniteElement(r); // Legendre polynomials const Matrix<Real_wp>& pol_leg = tet.GetLegendrePolynomial(); // use EvaluateJacobiPolynomial to evaluate Pn(2*x-1) VectReal_wp Pn; Real_wp x = 0.2; // x in [0, 1] EvaluateJacobiPolynomial(pol_leg, r+1, 2.0*x - 1.0, Pn);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
GetCoefLegendre
Syntax
| const VectReal_wp& GetCoefLegendre() const |
This method returns the coefficient used to normalize Legendre polynomials stored in the class (used for orthogonal polynomials ψj). With these coefficients, you have the orthonormality of Legendre polynomials in [0, 1] :
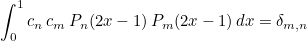
Example :
int r = 4; // polynomial degree TetrahedronGeomReference tet; tet.ConstructFiniteElement(r); // Legendre polynomials const Matrix<Real_wp>& pol_leg = tet.GetLegendrePolynomial(); // and coefficients of normalization const VectReal_wp& coef_leg = tet.GetCoefLegendre(); // use EvaluateJacobiPolynomial to evaluate Pn(2*x-1) VectReal_wp Pn; Real_wp x = 0.2; // x in [0, 1] EvaluateJacobiPolynomial(pol_leg, r+1, 2.0*x - 1.0, Pn); // multiplying by coefficient for (int i = 0; i ≤ r; i++) Pn(i) *= coef_leg(i);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
GetInvWeightPolynomial
Syntax
| const VectReal_wp& GetInvWeightPolynomial() const |
This method returns the coefficient used to normalize orthogonal polynomials ψj stored in the class. With these coefficients, you have the orthonormality of orthogonal polynomials in the unit tetrahedron :
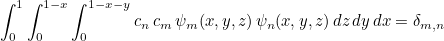
The coefficients cn are returned by GetInvWeightPolynomial.
Example :
int r = 4; // polynomial degree TetrahedronGeomReference tet; tet.ConstructFiniteElement(r); // coefficients of normalization const VectReal_wp& coef_psi = tet.GetInvWeightPolynomial(); // ComputeValuesPhiOrthoRef fills c_m psi_m R3 pt(0.2, 0.1, 0.3); VectReal_wp psi; tet.ComputeValuesPhiOrthoRef(pt, psi);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
GetNumOrtho3D
Syntax
| const Array3D<int>& GetNumOrtho3D() const |
This method returns the numbering for orthogonal polynomials.
Example :
int r = 4; // polynomial degree
TetrahedronGeomReference tet;
tet.ConstructFiniteElement(r);
// coefficients of normalization
const VectReal_wp& coef_psi = tet.GetInvWeightPolynomial();
// numbers
const Array3D<int>& num = tet.GetNumOrtho3D();
// triple loop
for (int i = 0; i ≤ r; i++)
for (int j = 0; j < r-i; j++)
for (int k = 0; k < r-i-j; k++)
{
// number for orthogonal polynomial
int p = num(i, j, k);
}
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
GetOddJacobiPolynomial
Syntax
| const Vector<Matrix<Real_wp> >& GetOddJacobiPolynomial() const |
This method returns the jacobi polynomials Pj2i+1, 0 stored in the class.
Example :
int r = 4; // polynomial degree
TetrahedronGeomReference tet;
tet.ConstructFiniteElement(r);
// jacobi polynomials for odd numbers
const Vector<Matrix<Real_wp> >& jac = tet.GetOddJacobiPolynomial();
// coefficients of normalization
const Matrix<Real_wp&>& coef = tet.GetCoefOddJacobi();
// evaluating polynomials P_j^{2i+1, 0} for a given i
int i = 2; Real_wp x = 0.4; VectReal_wp Pj;
EvaluateJacobiPolynomial(jac(i), r+1-i, 2.0*x - 1, Pj);
// multiplication by weights
for (int j = 0; j < Pj.GetM(); j++)
Pj(j) *= coef(i, j);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
GetCoefOddJacobi
Syntax
| const Matrix<Real_wp>& GetCoefOddJacobi() const |
This method returns the coefficient that normalizes jacobi polynomials Pj2i+1, 0 stored in the class :
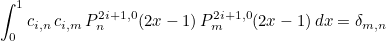
Example :
int r = 4; // polynomial degree
TetrahedronGeomReference tet;
tet.ConstructFiniteElement(r);
// jacobi polynomials for odd numbers
const Vector<Matrix<Real_wp> >& jac = tet.GetOddJacobiPolynomial();
// coefficients of normalization
const Matrix<Real_wp&>& coef = tet.GetCoefOddJacobi();
// evaluating polynomials P_j^{2i+1, 0} for a given i
int i = 2; Real_wp x = 0.4; VectReal_wp Pj;
EvaluateJacobiPolynomial(jac(i), r+1-i, 2.0*x - 1, Pj);
// multiplication by weights
for (int j = 0; j < Pj.GetM(); j++)
Pj(j) *= coef(i, j);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
GetEvenJacobiPolynomial
Syntax
| const Vector<Matrix<Real_wp> >& GetEvenJacobiPolynomial() const |
This method returns the jacobi polynomials Pj2i+2, 0 stored in the class.
Example :
int r = 4; // polynomial degree
TetrahedronGeomReference tet;
tet.ConstructFiniteElement(r);
// jacobi polynomials for even numbers
const Vector<Matrix<Real_wp> >& jac = tet.GetEvenJacobiPolynomial();
// coefficients of normalization
const Matrix<Real_wp&>& coef = tet.GetCoefEvenJacobi();
// evaluating polynomials P_j^{2i+2, 0} for a given i
int i = 2; Real_wp x = 0.4; VectReal_wp Pj;
EvaluateJacobiPolynomial(jac(i), r+1-i, 2.0*x - 1, Pj);
// multiplication by weights
for (int j = 0; j < Pj.GetM(); j++)
Pj(j) *= coef(i, j);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
GetCoefEvenJacobi
Syntax
| const Matrix<Real_wp>& GetCoefEvenJacobi() const |
This method returns the coefficient that normalizes jacobi polynomials Pj2i+2, 0 stored in the class :
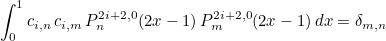
Example :
int r = 4; // polynomial degree
TetrahedronGeomReference tet;
tet.ConstructFiniteElement(r);
// jacobi polynomials for even numbers
const Vector<Matrix<Real_wp> >& jac = tet.GetEvenJacobiPolynomial();
// coefficients of normalization
const Matrix<Real_wp&>& coef = tet.GetCoefEvenJacobi();
// evaluating polynomials P_j^{2i+2, 0} for a given i
int i = 2; Real_wp x = 0.4; VectReal_wp Pj;
EvaluateJacobiPolynomial(jac(i), r+1-i, 2.0*x - 1, Pj);
// multiplication by weights
for (int j = 0; j < Pj.GetM(); j++)
Pj(j) *= coef(i, j);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReferenceInline.cxx
ConstructRegularPoints
Syntax
| static void ConstructRegularPoints( | int r, VectReal_wp& points_1d, VectR2& points_2d, const Matrix<int>& NumNodes2D, VectR3& points_3d, const Array3D<int>& NumNodes3D) |
This method computes the nodal points of the tetrahedron with a regular spacing. The nodes numbering is given for the triangle and tetrahedron.
Parameters
- r (in)
- order of approximation
- points_1d (out)
- 1-D nodal points
- point_2d (out)
- 2-D nodal points (for the unit triangle)
- NumNodes2D (in)
- 2-D nodes numbering
- point_3d (out)
- 3-D nodal points (for the unit tetrahedron)
- NumNodes3D (in)
- 3-D nodes numbering
Example :
int r = 3; // polynomial degree
Matrix<int> NumNodes2D(r+1, r+1);
NumNodes2D.Fill(-1);
// filling the node numbers : NumNodes2D(i, j) is the number of the node that will located at x_i, y_j
int num = 0;
for (int i = 0; i ≤ r; i++)
for (int j = 0; j ≤ r-i; j++)
NumNodes2D(i, j) = num++;
Array3D<int> NumNodes3D(r+1, r+1, r+1);
NumNodes3D.Fill(-1);
// filling the node numbers : NumNodes3D(i, j, k) is the number of the node that will located at x_i, y_j, z_k
num = 0;
for (int i = 0; i ≤ r; i++)
for (int j = 0; j ≤ r-i; j++)
for (int k = 0; k ≤ r-i-j; k++)
NumNodes3D(i, j, k) = num++;
// then we compute nodal points with the provided numbering
VectReal_wp points1d; VectR2 points2d; VectR3 points3d;
TetrahedronGeomReference::ConstructRegularPoints(r, points1d, points2d, NumNodes2D, points3d, NumNodes3D);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReference.cxx
ConstructLobattoPoints
Syntax
| static void ConstructLobattoPoints( | int r, VectReal_wp& points_1d, VectR2& points_2d, VectR3& points_3d) |
This method computes the nodal points of the tetrahedron with a small Lebesgue constant. The constructed points are Hesthaven's points (based on an anology with electrostatic's equilibrium). The 1-D nodal points will be equal to Gauss-Lobatto points and 2-D nodal points will coincide with Hesthaven's points of the unit triangle.
Parameters
- r (in)
- order of approximation
- points_1d (out)
- 1-D nodal points
- point_2d (out)
- 2-D nodal points
- point_3d (out)
- 3-D nodal points
Example :
int r = 3; // polynomial degree // then we compute nodal points for the required order VectReal_wp points1d; VectR2 points2d; VectR3 points3d; TetrahedronGeomReference::ConstructLobattoPoints(r, points1d, points2d, points3d);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReference.cxx
ComputeValuesPhiOrthoRef
Syntax
| void ComputeValuesPhiOrthoRef( | const R3& pt_loc, VectReal_wp& psi) |
This method evaluates the orthogonal functions ψj (as defined in the section devoted to the class TetrahedronGeomReference).
Parameters
- pt_loc (in)
- point where the functions need to be evaluated
- psi (out)
- values psij(pt_loc)
Example :
int r = 3; // polynomial degree TetrahedronGeomReference tet; tet.ConstructFiniteElement(r); // then we can evaluate orthogonal polynomials on a point of the unit tetrahedron R3 pt(0.2, 0.4, 0.1); VectReal_wp psi; tet.ComputeValuesPhiOrthoRef(pt, psi);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReference.cxx
ComputeGradientPhiOrthoRef
Syntax
| void ComputeGradientPhiOrthoRef( | const R3& pt_loc, VectR3& grad_psi) |
This method evaluates the gradient of orthogonal polynomials ψj (as defined in the section devoted to the class TetrahedronGeomReference).
Parameters
- pt_loc (in)
- point where the gradients need to be evaluated
- grad_psi (out)
- grad(psij)(pt_loc)
Example :
int r = 3; // polynomial degree TetrahedronGeomReference tet; tet.ConstructFiniteElement(r); // then we can evaluate the gradient orthogonal polynomials on a point of the unit tetrahedron R3 pt(0.2, 0.4, 0.1); VectR3 grad_psi; tet.ComputeGradientPhiOrthoRef(pt, grad_psi);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReference.cxx
ComputeOrthogonalFunctions
Syntax
| void ComputeOrthogonalFunctions(int r) const |
This method constructs the orthogonal functions ψj. If you call ConstructFiniteElement, this method is alreay called. If you call only ComputeOrthogonalFunctions, the shape functions will not be available.
Example :
int r = 3; TetrahedronGeomReference tet; // constructing orthogonal polynomials tet.ComputeOrthogonalFunctions(r); // evaluating orthogonal functions R3 pt_loc(0.2, 0.4, 0.1); VectReal_wp psi; tet.ComputeValuesPhiOrthoRef(pt_loc, psi);
Location :
FiniteElement/Tetrahedron/TetrahedronGeomReference.hxx FiniteElement/Tetrahedron/TetrahedronGeomReference.cxx