Time-harmonic and unsteady elasticity equations
Elastodynamics
In time-harmonic domain, we are solving the following equation :
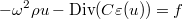
where C is the elasticity tensor appearing in Hooke's law, u is the displacement and ε(u) is the strain tensor. This tensor can be isotropic, and Lame coefficients (or Young's modulus/Poisson's ratio) are provided in the data file through field Materiau Dielec :
# you can enter Lame coefficients : # MateriauDielec = ref ISOTROPE rho lambda mu MateriauDielec = 1 ISOTROPE 1.2 2.4 0.8 # you can specify Young's modulus and Poisson's ratio # MateriauDielec = ref YOUNG_POISSON rho E nu MateriauDielec = 2 ISOTROPE 2700 6.9e10 0.34 # you can directly enter elasticity tensor C for orthotropic material # in 2-D : MateriauDielec = ref ORTHOTROPE rho c0000 c0011 c1111 c0101 # in 3-D : MateriauDielec = ref ORTHOTROPE rho c0000 c0011 c0022 c1111 c1122 c2222 c0101 c0202 c1212 MateriauDielec = 3 ORTHOTROPE 1.2 2.4 4.5 1.3 3.7 # in 2-D : MateriauDielec = ref ANISOTROPE rho c0000 c0011 c0001 c1111 c1101 c0101 # in 3-D : MateriauDielec = ref ANISOTROPE rho c0000 c0011 c0022 c0001 c0002 c0012 \ # c1111 c1122 c1101 c1102 c1112 c2222 \ # c2201 c2202 c2212 c0101 c0102 c0112 \ # c0202 c0212 c1212 MateriauDielec = 4 ANISOTROPE 1.2 2.4 4.5 1.3 3.7 0.2 0.5
Time-harmonic elastic equation is specified in class HarmonicElasticEquation. You can also solve static elastic equation with class ElasticEquation, which can be written as :
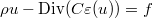
This last equation is solved in real numbers.
Reissner-Mindlin
In the case of thin plates, a classical model is the so-called Reissner-Mindlin model, which can be written as :
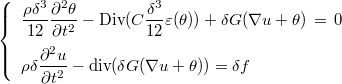
where the tensor C is defined with Young's modulus E and Poisson's ratio ν by the relationship
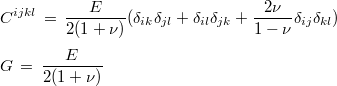
E and ν as entered as for classical elastic equations (with MateriauDielec field). You can also solve static Reissner-Mindlin equations :
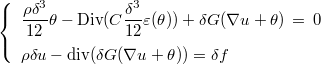
and time-harmonic Reissner-Mindlin equations
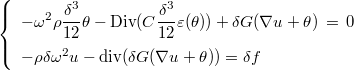
Fluid-structure interaction
We are considering the following set of equations
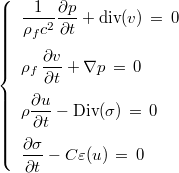
where u and σ are the displacements and the stresses and exist only in the solid, p and v the primitive of the pressure and displacement of the fluid and exist only in the fluid. The transmissions conditions between the fluid and the solid are the following ones
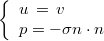
This problem is solved with explicit time-schemes only (leap frog or Runge-Kutta-like schemes).
Vibroacoustics
We also propose a coupling between Reissner-Mindlin equations (on a plate) and acoustics equation (in the volume), in order to avoid the meshing of a thin 3-D domain (the plate). The system of equations can be written as :
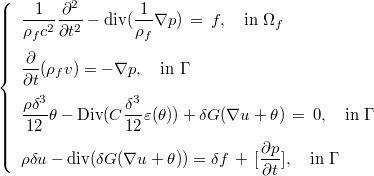
where ρf is the density of the fluid, c the velocity of sound waves in the fluid, p the primitive of the pressure, v the displacement of the fluid, θ and u displacements of the plate. We assume here that the normale is outward from Ω- to Ω+, and we denote the jump as :
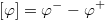
For this problem, one can only use hexahedral elements with first-order absorbing conditions