IMB > Recherche > Séminaires
Le 20 janvier 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Anne-Marie Bergé
Formes quadratiques définies positives : théorie de Morse, eutaxies et décomposition cellulaire
a2x793
Le 27 janvier 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Florian Ivorra
Réalisation l-adique de motifs mixtes..
Dans cet exposé, je donnerai les grandes lignes de la construction d'un foncteur de réalisation l-adique entier pour les motifs mixtes triangulés de V. Voevodsky sur un schéma noethérien séparé. Je présenterai la problématique d'où cette question est issue ainsi que de potentielles applications.
Le 3 février 2006
à 13:30
Séminaire de Théorie des Nombres
Salle de Conférences
Tim Browning Bristol
Représentation des entiers par les formes quadratiques..
Soit q(x1,...,xn) une forme quadratique. Cet exposé s'occupe de certains aspects de la résolubilité de l'équation q = k, pour un entier k positif ou nul. Par exemple, quand k=0 et q est indéfinie, on améliore un résultat classique de Cassels sur la taille de la solution minimale de l'équation q = 0. L'ingrédient principal dans la preuve est une forme moderne de la méthode du cercle.
Le 3 février 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Jean-Paul Allouche Orsay
Sur une intégrale de Ramanujan
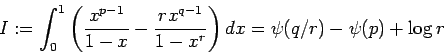
et 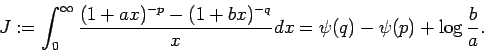
Ils se demandent alors, compte tenu de la similitude entre les deux membres de droite, si la première intégrale peut se déduire de la seconde. Nous répondons positivement à cette question et nous montrons que la valeur de l'intégrale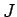 peut être déduite d'une expression classique due à Dirichlet de la fonction
peut être déduite d'une expression classique due à Dirichlet de la fonction 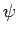 et de l'égalité classique (conséquence simple du théorème de Frullani-Cauchy)
et de l'égalité classique (conséquence simple du théorème de Frullani-Cauchy) 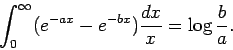
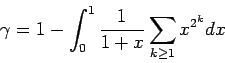
et 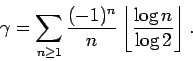
La première de ces deux égalités remonte en fait à Catalan, la seconde est connue sous le nom de série de Vacca pour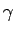 .
.
Le 10 février 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Philippe Gaborit Limoges
Interpolation polynomiale multivariée, codes et cryptographie
Dans cet exposé nous nous intéressons à l'interpolation polynomiale multivariée et à ses applications. Nous présenterons tout d'abord des applications connues comme le décodage en liste des codes de Reed-Solomon (pour lequel Madhu Sudan a recu le prix Nevanlinna), mais aussi des applications nouvelles comme le décodage en liste des effacements des codes de Reed-Muller ou encore l'application au calcul de l'immunité algebrique. Ce dernier concept a de trés forte aplications en cryptographie pour contrer les attaques algébriques qui récemment ont permis d'obtenir des attaques trés efficaces sur les registres linéaires filtrés, utilisés pour le chiffrement à flot ou sur certains systèmes à clé symétrique. Ensuite nous présenterons un nouvel algorithme qui permet d'effectuer l'interpolation polynomiale multivariée à plusieurs variables en temps quadratique, améliorant la complexité cubique connue jusqu'ici pour résoudre certains des problèmes précédents.
Le 24 février 2006
à 14:30
Séminaire de Théorie des Nombres
Salle 2
Stéphane Vénéreau Bale
Y a-t-il plusieurs Cn-1 dans Cn..
Plus précisément : deux hypersurfaces de Cn isomorphes à Cn-1 sont-elles toujours équivalentes à automorphisme (polynomial) de Cn près? Cette question, difficile, se résout positivement dans certains cas, avec des arguments topologiques et algébriques mais le cas général, à partir de n=3 reste inconnu; on connait même un plongement explicite de C^3 dans C4 dont on ne sait s'il est trivial ou non. Cette question est étroitement liée à d'autres problèmes de la géométrie algébrique affine comme, par exemple, la description du groupe des automorphismes polynomiaux de Cn. On peut également étudier des versions plus algébriques de cette question (remplaçons C par un méchant anneau) et trouver, là, des contre-exemples. }
Le 3 mars 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Raf Clückers
Sommes exponentielles: Conjectures de Denef - Sperber et d'Igusa, et introduction à une compréhension motivique
Je parlerai d'une solution positive des conjectures de Denef - Sperber pour les sommes exponentielles non-dégénérées. Il s'agit de bornes optimales pour des sommes exponentielles, non pas sur des corps finis, mais sur des anneaux finis comme les entiers modulo N avec N un entier positif. (Sur les corps finis, une théorie vaste est connue due à Deligne, Katz, Laumon et autres.) Par factorisation en nombres premiers, le cas important est quand N est une puissance d'un nombre premier, et alors on parle de sommes exponentielles p-adiques. L'uniformité en p et en la puissance de p est difficile à comprendre mais il y a des conjectures d'Igusa, de Denef et Sperber qui donnent des bornes très précises, en beaucoup de cas conjecturalement optimales. Si on somme exp(2i pi f(x)/N) sur les nombres x entre 0 et N-1 dans le cas ou f est nondégénéré par rapport à son polyèdre de Newton, on est dans le cas de la conjecture de Denef et Sperber que je présente. Deuxième thème: avec F. Loeser, et indépendemment par Kashdan et Hrushovski, on comprend finalement la nature motivique qualitative de ses sommes quand p bouge. Malheureusement, cette compréhension qualitative ne donne que des bornes rudes et donc pas assez pour les conjectures mentionnées.
Le 3 mars 2006
à 15:30
Séminaire de Théorie des Nombres
Salle de Conférences
Teturo Kamae Matsuyuma University
Numeration systems and their zeta-functions
Le 10 mars 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Emmanuel Kowalski
Petits écarts entre nombres premiers, d'après Goldston, Graham, Pintz, Yildirim
a2x811
Le 17 mars 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Daniel Caro Durham
Fonctions zêta de Weil et cohomologies p-adiques
\def\Q{\mathbb{Q}} \def\D{\mathcal{D}} Le calcul des fonctions zêta de Weil d'une variété algébrique $X$ sur un corps fini de caractéristique $p$ permet d'obtenir des applications cryptographiques. Nous rappellerons leurs différentes interprétations cohomologiques via des méthodes $l$-adiques ($l$ est un premier différent de $p$) ou $p$-adiques (i.e., on travaille sur $\Q_l$ ou $\Q_p$). Ces fonctions se généralisent de multiples façons en considérant en plus de la variété $X$, un objet $E$ (e.g. $\Q_l$-faisceaux constructibles, $F$-cristaux, $F$-isocristaux, $F$-complexes de $\D$-modules arithmétiques) vivant sur $X$. On définit ainsi des fonctions $L$ associées à $E$ (la fonction $L$ du coefficient «constant» redonne la fonction zeta de Weil). Afin d'obtenir une bonne cohomologie $p$-adique sur $X$, i.e., satisfaisant toutes les conditions requises pour devenir une «cohomologie de Weil», l'idée de Berthelot fut de construire une théorie arithmétique des $\D$-modules. Nous donnerons une formule cohomologique des fonctions $L$ associées aux $F$-complexes de $\D$-modules arithmétiques. Nous expliquerons comment cela résulte ou s'inspire des précédentes interprétations cohomologiques.
Le 17 mars 2006
à 15:30
Séminaire de Théorie des Nombres
Salle de Conférences
Frank Vallentin Amsterdam
Semidefinite programming bounds
Finding the stability number of a graph (A stable set is a subset of vertices in which any two are not adjacent and the stability number is the size of a maximum stable set.) is a well-studied problem in combinatorial optimization. It is NP-hard to compute and it is also difficult to approximate it. We propose an algorithm for computing a monotonic decreasing series of upper bounds for the stability number of a given graph. In every step of the series one has to solve a semidefinite programming problem. The algorithm is especially well-suited for highly symmetric graphs: By using harmonic analysis on finite groups one can (sometimes dramatically) reduce the size of the semidefinite programming problems. As a major example we consider the graph H(n,d). Its vertices are binary code words of length n and two vertices are adjacent if their Hamming distance is at most d - 1. Finding a maximum stable set in H(n,d) is equivalent to determining an optimal binary code of length n with minimum norm d. It turns out the the first step of our algorithm gives the classical linear programming bound due to Delsarte and that the second step gives the recent bound of Schrijver. This is joint work with Monique Laurent.
Le 24 mars 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Guillaume Hanrot INRIA\, Nancy
Moyennes de fonctions arithmétiques sur les entiers friables
Les problèmes de friabilité (déntiers, d'idéaux\dots) sont omniprésents dans la théorie algorithmique des nombres modernes, et leur étude est indispensable pour espérer, par exemple, une analyse rigoureuse des algorithmes de factorisation d'entiers. \medskip Je présenterai des résultats généraux permettant d'obtenir un développement asymptotique d'expressions de la forme $$\sum_{{n \leq x, P^+(n) \leq y}} f(n),$$ dans un large domaine, où $f$ est une fonction multiplicative dont la série de Dirichlet est du type $$G(s) \prod_{j=1}^r \zeta_{K_j}^{\lambda_j}(s),$$ sous des hypothèses bénignes sur la fonction $G$. Travail commun avec G. Tenenbaum et J. Wu.
Le 24 mars 2006
à 15:30
Séminaire de Théorie des Nombres
Salle de Conférences
Masayoshi Miyanishi Kwansei Gakuin University
Quelques pensées sur le théorème d'Ax
Le théorème d'Ax, souvent appelé théorème d'Ax, Borel et Grothendieck, séxprime comme suit. Théorème. (Ax, 1969) Soient Y un schéma et X un schéma de type fini sur Y. Soit f: X --> X un Y-endomorphisme injectif. Alors f est bijectif. Il généralise un résultat de D. J. Newman sur le cas X=R^2, déjà généralisé au cas X=R^n avec n quelconque par Bialynicki-Birula et Rosenlicht. Ce théorème a récemment attiré beaucoup d'attention en géométrie algébrique affine, en liaison avec la conjecture Jacobienne. Nous allons le revisiter et considérer ses variantes. Le thème principal de l'exposé sera les endomorphismes des variétés algébriques, pas nécessairement injectifs.
Le 31 mars 2006
à 14:30
Séminaire de Théorie des Nombres
Salle 1
Lara Thomas Lausanne
Structure galoisienne et combinatoire dans les extensions.. d'Artin-Schreier
Soit L/K une extension de corps locaux de degré [L : K] = car K = p > 0. Notons OK et OL les anneaux d'entiers correspondants. Lorsque L/K est totalement ramifiée, on étudie la structure de OL comme module sur l'ordre A associé à l'extension L/K. À l'aide d'arguments essentiellement combinatoires nous donnerons un critère purement algébrique pour que OL soit libre sur A : ce résultat renforce des travaux récents de Aiba et Lettl et s'obtient à partir d'une preuve indépendante. Nous présenterons également un résultat plus général qui permet de calculer le nombre minimal de générateurs de OL comme A-module à partir d'un développement en fraction continue.
Le 7 avril 2006
à 14:30
Séminaire de Théorie des Nombres
Salle 2
David Vauclair Besancon
Autour de la conjecture de Greenberg généralisée...
La conjecture de Greenberg Généralisée (GG) peut être considérée comme une généralisation lointaine de la conjecture de Vandiver, qui prédit que le nombre de classes de Q(zeta_p)^+ nést pas divisible par p. Le but de cet exposé est l'énoncé d'une version faible (GGf) de la conjecture (GG), ainsi que sa démonstration, sous certaines hypothèses.
Le 14 avril 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Xavier Caruso Paris XIII
Conjecture de l'inertie modérée de Serre
Soit K un corps complet pour une valuation discrète v, de caractéristique nulle et dont on suppose le corps résiduel algébriquement clos de caractéristique p. Soit X un schéma propre et lisse sur K à réduction semi-stable sur l'anneau des entiers de K. En 1972, Serre demandait si les représentations galoisiennes données par la cohomologie étale de X (sur une clôture algébrique) étaient bornées dans un certain sens (qu'il explicitait totalement). Après un bref rappel historique des progrès sur la question de Serre, nous présenterons les méthodes modernes d'attaque d'un tel problème qui reposent principalement sur l'introduction des cohomologies log-cristalline et log-syntomique et l'existence de théorèmes de comparaison entre celles-ci et la cohomologie étale. Enfin nous montrerons comment ces méthodes permettent de prouver complètement le résultat conjecturé par Serre.
Le 28 avril 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Andrea Surroca Lausanne
Valeurs algébriques de fonctions transcendantes
Étant donnée une fonction f analytique et transcendante sur C(z), on s'intéresse à l'ensemble S_f des points algébriques en lesquels la fonction f prend des valeurs algébriques. Par exemple, pour la fonction exponentielle, S_f = {0}, et si on pose f(z) = 2^z, alors S_f = Q. On sait, d'après Stäckel, qu'il existe des fonctions entières et transcendantes prenant des valeurs algébriques en tous les points algébriques, cést-à-dire, telles que S_f soit une cloture algebrique de Q. En introduisant un contrôle sur le degré et la hauteur, nous donnerons une majoration sur le nombre de points algébriques où une fonction analytique transcendante prend des valeurs algébriques.
Le 19 mai 2006
à 14:30
Séminaire de Théorie des Nombres
Salle 2
John Swallow Davidson College
La structure galoisienne de la cohomologie galoisienne
Soient p un nombre premier, F un corps contenant une racine primitive p-ième d e l'unité et E/F une extension galoisienne de degré p, de groupe de Galois G. S oit G_E le groupe de Galois absolu de E. Les groupes de cohomologie H^i(E,Fp)=H ^i(G_E,Fp) possèdent une structure naturelle de FpG-modules et se decomposent e n somme directe de modules indecomposables. Borevic et Faddeev ont donné, dans les années soixantes, les décompositions de E^*/E^*p---le cas i=1---pour les cor ps locaux. Nous nous intéresserons dans cet exposé au cas i=1 pour des corps q uelconques, puis, utilisant la conjecture de Bloch-Kato, nous étudierons les cas i>1. La surprise vient du fait qu'il existe des FpG-modules indecomposables qu i n'apparaissent jamais dans de telles décompositions. Nous donnerons ensuite q uelques conséquences de ces résultats, notamment une généralisation de la formul e de Schreier pour G_E et des liens avec les groupes de Demuskin et des characte ristiques d'Euler-Poincaré de G_E. Il s'agit d'un travail en collaboration avec J. Labute, N. Lemire, et J. Minac.
Le 2 juin 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Tanguy Rivoal Grenoble
Un exposant de densité en approximation rationnelle
Le 16 juin 2006
à 14:30
Séminaire de Théorie des Nombres
Salle de Conférences
Jean-François Jaulent
Nombres de Weil l-adiques
Nous introduisons la notion de nombre de Weil l-adique par analogie avec la notion classique de nombre de Weil à linfini ; et nous en étudions quelques propriétés en liaison avec les plongements et les valeurs absolues réelles ou l-adiques des corps de nombres. Nous en tirons diverses applications à la théorie dIwasawa des tours cyclotomiques.
Le 23 juin 2006
à 14:30
Séminaire de Théorie des Nombres
Salle 1
Douglas Ulmer Arizona
Variétés jacobiennes de rang élévé sur les corps de fonctions
Le 6 octobre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Emmanuel Kowalski
Crible, marches aléatoires sur les groupes et propriété (T)
L'exposé présentera un mélange (agréable espérons-le) de théorie des nombres, d'algèbre, d'analyse et de probabilités pour arriver au résultat suivant~: si l'on part de la matrice identité $X_0$ (de taille $n$ au moins égale à $2$), et que l'on effectue la marche au hasard infinie déterminée par $X_{k+1}=X_k E_k$, où $E_k$ est une matrice élémentaire avec un coefficient $\pm 1$ hors de la diagonale, choisie au hasard pour chaque $k$, alors presque sûrement les polynômes caractéristiques des matrices $X_k$ ainsi obtenues seront irréductible à partir d'un certain rang.
Le 13 octobre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Christine Bachoc
Nouvelles bornes pour le nombre de contact et programmation semi-définie
Le nombre de contact (ou plus joliment mais en anglais \emph{kissing number}) de la dimension $n$, noté $\tau(n)$, compte le nombre maximum de sphères de rayon $1$ que l'on peut coller à une même sphère de rayon $1$. On ne connait la valeur exacte de $\tau(n)$ que pour les dimensions $n=1,2,3,4,8,24$. Pour les autres valeurs de $n$, on connait seulement une borne supérieure, obtenue en général par la méthode de la programmation linéaire (LP) due à Philippe Delsarte. Dans un travail en commun avec Frank Vallentin, nous développons une généralisation de cette methode, qui fournit une borne comme solution d'un problème de programmation semi définie (SDP). Cette nouvelle borne s'avère meilleure que la borne LP et nous permet de donner une preuve uniforme pour la valeur connue de $\tau(n)$ pour $n=3,4,8,24$, et d'ameliorer les bornes connues pour $\tau(n)$ pour toutes les autres valeurs de $n=5$ à $n=10$. Elle s'applique aussi à d'autres questions de théorie des codes et de géométrie sphérique qui seront abordées dans l'exposé.
Le 20 octobre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle 2
Sandra Rozensztajn Strasbourg
Comparaison entre cohomologie étale p-adique et cristalline sur certaines variétés de Shimura
Soit X un modèle entier d'une variété de Shimura, associée à un groupe réductif G. On peut associer aux représentations de G sur Zp deux types de faisceaux : des cristaux sur la fibre spéciale de X, et des faisceaux localement constants pour la topologie étale sur la fibre générique. On étudie la relation entre la cohomologie de ces deux types de faisceaux.
Le 27 octobre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Marius van der Put Groningen
Searching solutions for differential equations
We focus on the following problem, posed by L. Fuchs: For which linear differential equations L(y) = y(n) + an-1y(n-1)+ ... + a1y(1) + a0y = 0 can one express the solutions in terms of solutions of linear differential equations of degree ≤ n? Gino Fano published in 1900 a remarkable paper on this theme. It seems to have been forgotten until M. F. Singer took up this theme around 1985 . He proved and disproved certain statements and conjectures of Fano. We will try to present a systematic treatment of Fano's paper, due to Nguyen Khuong Ann and myself.
Le 10 novembre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Renaud Coulangeon
Designs sphériques et fonctions zêta de réseaux
La fonction zêta d'Epstein est une généralisation multidimensionnelle de la fonction zêta de Riemann : à un réseau euclidien $L$ de dimension $n$ on associe la série $$ \zeta(L,s):= \sum_{x \in L - \{0\}} ||x||^{-2s},$$ qui converge pour $\mathrm{Re}(s) > \frac{n}{2}$ et admet un prolongement analytique à $\mathbb{C}\setminus\left\lbrace \frac{n}{2}\right\rbrace $. On s'intéresse aux réseaux qui, à $s>0$ fixé ($s eq \frac{n}{2}$), minimisent $\zeta(L,s)$. Cette question, qui est liée à la question plus classique de la détermination des empilements de sphères réguliers les plus denses, apparait assez naturellement dans des contextes variés (géométrie, physique). Dans un article récent (Invent. Math. 165 (2006), no. 1, 115--151), Sarnak et Str"ombergsson montrent que les réseaux de racines $\mathbb{D}_4$ et $\mathbb{E}_8$, ainsi que le réseau de Leech $\Lambda_{24}$, réalisent un minimum local strict de $\zeta(L,s)$ pour tout $s>0$ ($s eq \frac{n}{2}$). Nous proposons une nouvelle preuve de ce résultat, conceptuellement plus simple, basée sur la notion de design sphérique. En outre, notre approche permet d'étendre le théorème de Sarnak et Str"ombergsson à toute une famille de réseaux (les "réseaux modulaires extremaux"), \textsl{via} des travaux de Bachoc et Venkov.
Le 10 novembre 2006
à 15:30
Séminaire de Théorie des Nombres
Salle de Conférences
Christophe Doche Macquarie
Moments des polynômes de Rudin-Shapiro et généralisations
Le 17 novembre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Kohji Matsumoto Nagoya
Mean square values of standard L-functions attached to Ikeda lifts
In general it is very difficult to determine the exact order of the mean square of standard L-functions attached to Siegel modular forms of higher degree. However, if the form is an image of Ikeda lifting, the situation is quite different. In this talk I will report that, in such a case, we can almost determine the exact order. (A part of this talk is a joint work with A. Sankaranarayanan.)
Le 24 novembre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Pierre-Marie Poloni Dijon
Peut-on déterminer si deux polynômes donnés sont équivalents ?
Deux polynômes $P,Q\in \bf{C} [X_1,\ldots,X_n]$ sont dits (algébriquement) équivalents s'il existe un automorphime polynomial $\varphi$ de $\bf{C} [X_1,\ldots,X_n]$ tel que $\varphi(P)=Q$. Savoir si deux polynômes donnés sont équivalents ou non est une question naturelle mais difficile en général. Dans cet exposé, on se propose d'illustrer, par des exemples explicites, le genre de difficultés que l'on rencontre. L' étude des plongements de certaines hypersurfaces de $\bf{C}^3$, dites hypersurfaces de Danielewski, jouera un rôle important dans la construction de ces exemples.
Le 8 décembre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Emmanuel Royer Clermont-Ferrand
Statistiques de deuxième ordre des petits zéros de fonctions L de puissances symétriques
Le 15 décembre 2006
à 14:00
Séminaire de Théorie des Nombres
Salle de Conférences
Marcus Wagner Berlin
On the computation of Hermite-Humbert constants for real quadratic number fields
In 1965 Harvey Cohn presented an algorithm for the numerical approximation of low-points for the Hilbert modular group of real quadratic number fields $K$ with $h(K)=1$. It turns out that in fact the low-points correspond to extreme Humbert forms of real quadratic number fields. For extreme Humbert forms we use the theory of Vorono"i and Coulangeon for characterization. In this talk we combine the advantages of known algorithms and Cohn's algorithm to obtain new examples of extreme Humbert forms. We are able to compute extreme Humbert forms for the fields $Q(\sqrt{7})$, $Q(\sqrt{11})$ and $Q(\sqrt{6})$.
Séminaire Théorie des Nombres
Responsables : Elena Berardini, Léo Poyeton.
J.-P. Allouche CNRS, LRI, Bâtiment 490 F-91405 Orsay Cedex (France) http://www.lri.fr/![]() allouche
allouche
Dans un article paru en 2000, B. Berndt et D. Bowman calculent deux intégrales dues à Ramanujan :
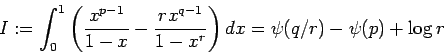
et
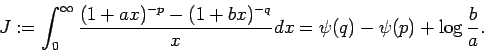
Ils se demandent alors, compte tenu de la similitude entre les deux membres de droite, si la première intégrale peut se déduire de la seconde. Nous répondons positivement à cette question et nous montrons que la valeur de l'intégrale
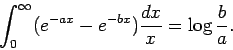
Il n'est pas sans intérêt d'indiquer deux expressions de la constante d'Euler ![]() que l'on peut déduire du calcul de l'intégrale
que l'on peut déduire du calcul de l'intégrale ![]() :
:
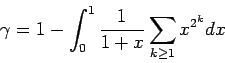
et
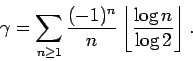
La première de ces deux égalités remonte en fait à Catalan, la seconde est connue sous le nom de série de Vacca pour



