Computation of eigenvalues and eigenvectors in Montjoie

For formulations of second order, the evolution problem is equal to

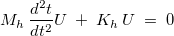
where M_h and K_h are the mass and stiffness matrix. The associated eigenvalue problem is equal to :

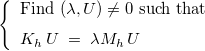
The eigenvale λ is associated with the square of the pulsation :

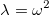
For formulations of first order, the evolution problem is equal to :

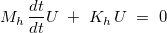
where M_h and K_h are the mass and stiffness matrix. The associated eigenvalue problem is equal to :

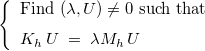
The eigenvale λ is associated with the pulsation :

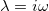
For the first-order problems, the interested eigenvalues are often located on the imaginary axis. The eigenmodes (λ, U) are computed via the interface of eigenvalue solvers achieved in Seldon. The class EigenProblemMontjoie is deriving from the class SparseEigenProblem with some overloads of methods in order to handle finite element matrices stored in Montjoie. Below, an example of use of this class is detailed :

// construction of EllipticProblem class
EllipticProblem<TypeElement, TypeEquation> var;
ReadInputFile(input_file, var);
// ...
var.ComputeMassMatrix();

// then you can declare a solver relying on the considered problem
All_LinearSolver<TypeElement, TypeEquation> glob_solver(var);
// you can read parameters of the data file :
ReadInputFile(input_file, glob_solver);

// you can select the solver, for example a direct solver
glob_solver.SetDirectSolver();

// then you declare an eigenvalue problem that will use
// the linear solver to compute the eigenvalues
EigenProblemMontjoie<TypeElement, TypeEquation>
eigen_solver(var, glob_solver);
// parameters can be read in a file
ReadInputFile(input_file, eigen_solver);

// effective computation of eigenvalues and eigenvectors
Vector<Complexe> lambda_real, lambda_imag;
Matrix<Complexe> eigen_vectors;
GetEigenvaluesEigenvectors(eigen_solver, lambda_real, lambda_imag, eigen_vectors);