Résumé des activités de recherche antérieures à Inria
Stage de DEA à l'IMFT : Ce stage
concernait la transition laminaire-turbulent 2D dans des
écoulements cisaillés. Tout d'abord, un code de calcul
éléments finis résolvant les équations de Navier-Stokes a
intensivement été testé afin d'apporter des améliorations et
de le valider. Ensuite, aprês avoir implanté des conditions
aux limites de type non-réflectif, la transition laminaire
turbulent d'un écoulement autour d'une aile d'avion de type
NACA12 a été étudié.
Thèse au LEMTA : Ce travail était une réflexion autour de l'apport potentiel de la réduction de modêles au contrà´le d'écoulement. L'originalité de l'étude était de coupler une approche par contrà´le optimal, à une modélisation de la dynamique contrà´lée de l'écoulement par modêle réduit construit par Décomposition Orthogonale aux valeurs Propres (POD). La démarche proposée était illustrée sur l'écoulement de sillage d'un cylindre circulaire en régime laminaire dont on cherchait à minimiser la traàŽnée aérodynamique. La loi de contrà´le de l'écoulement était la vitesse tangentielle sinusoà¯dale imposée au cylindre. Afin de valider a posteriori la méthode d'optimisation proposée, une étude numérique de l'influence des paramêtres de contrà´le sur la trainée a d'abord été réalisée. Aprês s'àªtre intéressé à l'amélioration de la représentativité dynamique du modêle réduit POD (ajout de viscosité optimale, introduction de modes de translation), différentes stratégies de contrà´le ont été mises en oeuvre. Dans une premiêre phase, une base POD généralisée, représentative uniquement de champs de vitesse, a été construite. Cette base POD, susceptible a priori de prendre en compte l'ensemble des dynamiques de l'écoulement forcé, a été utilisée tout au long du processus d'optimisation. Dans une seconde phase, la base POD a été étendue au champ de pression puis une procédure adaptative de résolution a été adoptée. Deux algorithmes différents, le premier de nature heuristique, le second basé sur une méthode à région de confiance ont été successivement utilisés, pour déterminer quand la réactualisation du modêle réduit était nécessaire. Ces différentes stratégies de contrà´le ont permis de diminuer fortement la trainée, voire de la minimiser lorsque la méthode à région de confiance était utilisée. Les coà»ts numériques de ces approches sont extràªmement faibles en comparaison de ceux correspondant à une méthode de contrà´le optimal basée sur les équations de Navier-Stokes.
Stage post-doctoral au LEMTA: Ce stage concernait le contrà´le dans les systêmes de réaction diffusion avec pour objectif une application à la modélisation des feux de foràªts et à la lutte. Une premiêre étape a consisté à réduire l'ordre du modêle de propagation de feu par l'utilisation de réseaux de neurones. Ce modêle réduit, quasiment non dégradé par rapport au modêle d'origine, a ensuite été utilisé avec succês dans une méthode inverse afin de déterminer l'origine de feux à partir de quelques mesures bruitées du front de flamme. Ensuite, j'ai déterminé la position optimale de capteurs à placer dans un feu afin de déterminer le front du feu, souvent indétectable en pratique. Ce travail servira de pour calibrer (assimilations de données) et valider le code de calcul.
Stage post-doctoral au MAB: Ce stage concerne l'amélioration des bases propres construites par POD. L'objectif est d'obtenir une base POD qui soit robuste ou facilement adaptative vis à vis des évolutions éventuelles de paramêtres du systême (nombre de Reynolds, paramêtres de contrôle, etc). Une méthode novatrice est utilisée. La base POD est construite a priori, par une méthode GMRES (voir méthodes de Krylov), sans avoir besoin de réalisations de l'écoulement. Les coefficients temporels sont quant à eux obtenus par une méthode de Galerkin non-linéaire par minimisation du résidu de l'opérateur de Navier-Stokes restreint à la base POD. Màªme si certains problêmes restent encore à résoudre, cette méthode semble três performante.
Aprês avoir obtenu une Licence puis une Maitrise de Mécanique en 1999 et 2000 respectivement, à l'Université Henri Poincaré de Nancy, j'ai décidé d'effectuer le D.E.A. de "dynamique des fluides" de Toulouse, que j'ai obtenu en 2001. Mes activités de recherche lors de mon stage de D.E.A., de ma thèse et de mon contrat post-doctoral ont été consacrées à l'analyse, la simulation, la modélisation, le contrôle actif d'écoulements laminaires, transitionnels et turbulents, ainsi qu'au contrôle de systêmes complexes (feux de foràªts).
Mon stage de D.E.A., effectué
conjointement au sein de l'Institut de Mécanique des Fluides
de Toulouse (IMFT) et de
l'école Nationale Supérieure d'Electrotechnique,
d'Electronique, d'Informatique, d'Hydraulique et des
Télécommunications (ENSEEIHT),
a
été encadré par Mme Marianna Braza (Directeur de recherche
CNRS, IMFT) et Mr Daniel Ruiz (Maitre de conférence,
E.NSEEIHT). Ces travaux concernaient principalement
l'analyse physique de la transition laminaire-turbulent 2D
dans des écoulements cisaillés. Cette étude a été réalisée
à l'aide d'un code éléments finis résolvant les
équations de Navier-Stokes 2D par un schéma
prédicteur-correcteur, de type correction de pression.
L'écriture de ce code, développé dans le cadre d'une
collaboration entre l'IMFT et l'ENSEEIHT, venait juste de
s'achever. Il était donc nécessaire de le tester, et d'en
déterminer les ordres de discrétisation en espace et en
temps. Pour ce faire, j'ai comparé les champs de vitesse et
de pression, obtenus numériquement, aux solutions
analytiques correspondant au tourbillon de Green-Taylor. Par
la suite, pour simuler des écoulements cisaillés, et
notamment l'écoulement autour d'un profil d'aile, il a fallu
implémenter dans ce code des conditions aux limites de sortie de type
non-réflectif afin de réduire la taille du
maillage. De telles conditions limites permettent de laisser
sortir librement les tourbillons du domaine de calcul, sans
aucune réflexion. Ceci a été effectué avec succês dans le
cas d'une zone de mélange. Enfin, une partie importante de
cette étude était d'analyser physiquement la transition
laminaire-turbulent 2D de l'écoulement autour d'une aile de
type NACA12 pour un nombre de Reynolds égal à 800, et
cela pour différentes incidences de l'aile variant de 12°
à 20°. Les résultats de cette étude étaient alors
comparés aux résultats de Y. Hoarau (IMFT) obtenus à
l'aide d'un solveur volumes finis tridimensionnels. Une três
bonne concordance a alors été observée pour les nombres de
Strouhal caractéristiques de l'allée de Von Karman ainsi que
pour les coefficients de portance et de trainée. Ces
résultats ont permis de valider une autre approche de la
simulation numérique des équations de Navier-Stokes et de
sceller une collaboration prometteuse entre l'IMFT et
l'ENSEEIHT.
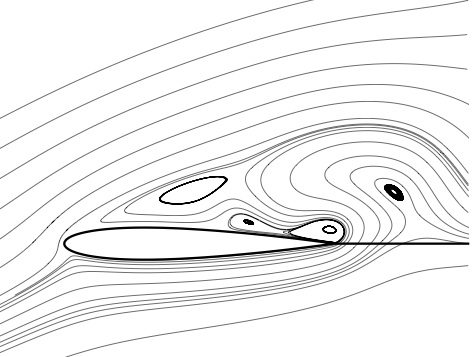
Fig : Simulation du sillage d'une aile NACA12.

Fig : Simulation du sillage d'une aile NACA12.
Le contrôle d'écoulement
Optimiser l'aérodynamique
interne et externe d'un avion par contrôle des écoulements a toujours été
un enjeu majeur pour le développement du transport
aéronautique. En effet, réduire par contrôle (actif ou
passif) la trainée permettrait d'augmenter l'autonomie en
vol, réduisant ainsi les coà»ts opérationnels. Cependant les
bénéfices potentiels du contrôle d'écoulement ne sont pas
limités au domaine économique : réduction de l'émission de
gaz polluants ou de la nuisance sonore sont largement aussi
attendus. Les expérimentations sur le contrà´le d'écoulement
ont été initiées il y a plus de 70 ans par Prandtl (1935).
Depuis cette date, les travaux expérimentaux n'ont jamais
cessés (Gad-el-Hak,
2000). Les approches théoriques du contrà´le
d'écoulement n'ont pas, quant à elles, eu le màªme
développement. Depuis une dizaine d'années, l'informatique,
la théorie du contrà´le, les approches mathématiques liées
aux équations de Navier-Stokes, les méthodes numériques pour
la simulation en Mécanique des Fluides et la résolution de
problêmes d'optimisation ont atteint un niveau de maturité
suffisant pour pouvoir reconsidérer les problêmes de
contrà´le d'écoulement de maniêre plus moderne.
Configuration de l'étude
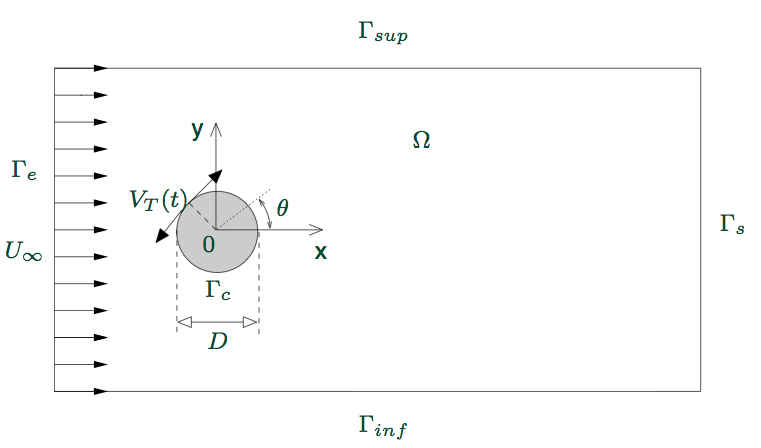
L'objectif de notre étude a été de contrà´ler le sillage instationnaire existant en aval d'un cylindre circulaire. D'un cà´té, c'est un écoulement suffisamment simple pour pouvoir àªtre étudié numériquement à un coà»t raisonnable. De l'autre, c'est une configuration représentative des écoulements décollés (En tant que tel, ce travail est en lien direct avec le Groupe De Recherche Contrà´le Des Décollements animé par A. Kourta (IMFT)). Pour des raisons de simplicité de mise en oeuvre numérique, ce travail est limité à des configurations bidimensionnelles et l'étude est réalisée pour Re=200. Dans le sillage laminaire, les grandeurs caractéristiques de l'écoulement présentent un comportement périodique en temps que l'on peut caractériser par son nombre de Strouhal $St$. On note $C_D$ le coefficient de trainée. Par la suite, le contrà´le de l'écoulement est exercé par rotation instationnaire du cylindre autour de sa génératrice. On impose un taux de rotation $\gamma(t)$ construit comme le rapport de la vitesse tangentielle du cylindre sur la vitesse à l'infini amont : $ \gamma(t)=V_T(t)/U_\infty. $ Pour $\gamma=0$ le coefficient de trainée moyen est égal à $C_D=1,40$. On se consacrera, par la suite, uniquement à la détermination d'une loi de contrôle harmonique $\gamma(t)=A\sin\left(2\pi St_f t\right)$ permettant de minimiser la trainée aérodynamique du cylindre, oû $A$ et $St_f$ sont respectivement l'amplitude et le nombre de Strouhal de forçage.
Méthodes numériques

L'objectif de notre étude a été de contrà´ler le sillage instationnaire existant en aval d'un cylindre circulaire. D'un cà´té, c'est un écoulement suffisamment simple pour pouvoir àªtre étudié numériquement à un coà»t raisonnable. De l'autre, c'est une configuration représentative des écoulements décollés (En tant que tel, ce travail est en lien direct avec le Groupe De Recherche Contrà´le Des Décollements animé par A. Kourta (IMFT)). Pour des raisons de simplicité de mise en oeuvre numérique, ce travail est limité à des configurations bidimensionnelles et l'étude est réalisée pour Re=200. Dans le sillage laminaire, les grandeurs caractéristiques de l'écoulement présentent un comportement périodique en temps que l'on peut caractériser par son nombre de Strouhal $St$. On note $C_D$ le coefficient de trainée. Par la suite, le contrà´le de l'écoulement est exercé par rotation instationnaire du cylindre autour de sa génératrice. On impose un taux de rotation $\gamma(t)$ construit comme le rapport de la vitesse tangentielle du cylindre sur la vitesse à l'infini amont : $ \gamma(t)=V_T(t)/U_\infty. $ Pour $\gamma=0$ le coefficient de trainée moyen est égal à $C_D=1,40$. On se consacrera, par la suite, uniquement à la détermination d'une loi de contrôle harmonique $\gamma(t)=A\sin\left(2\pi St_f t\right)$ permettant de minimiser la trainée aérodynamique du cylindre, oû $A$ et $St_f$ sont respectivement l'amplitude et le nombre de Strouhal de forçage.

Fig : configuration de l'écoulement.
Méthodes numériques
Le modêle de Navier-Stokes
est résolu par utilisation d'une méthode de projection
à trois pas (Chorin,
1968 ; Jin
et Braza, 1993) de type prédicteur-correcteur pour
la discrétisation en temps et par éléments finis de
type $P_1$ en espace.
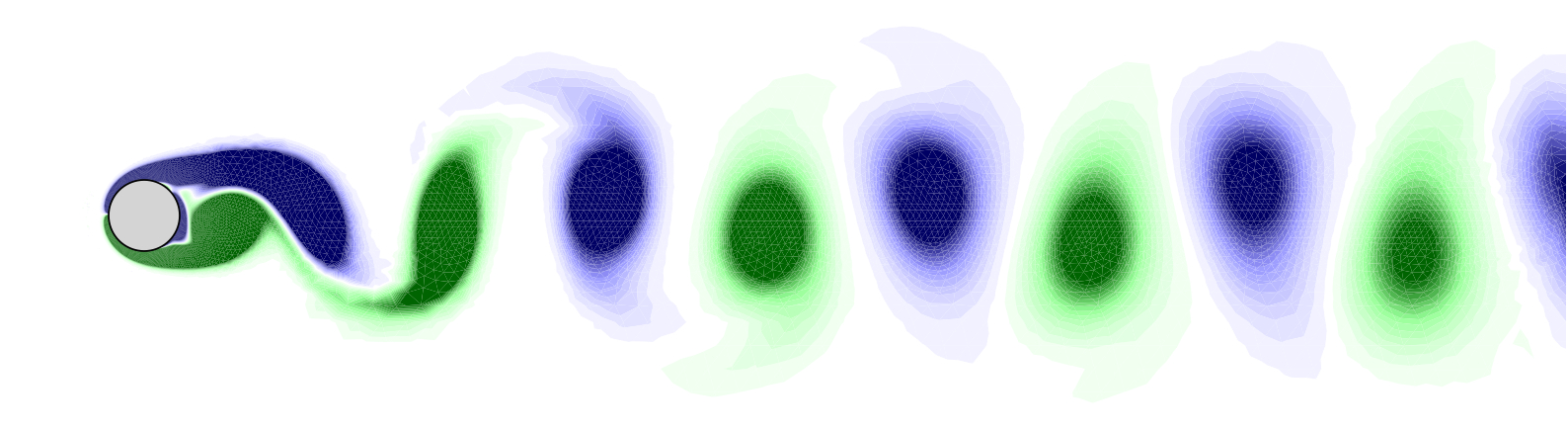
Fig : Sillage de l'écoulement naturel, non contrôlé.

Fig : Sillage de l'écoulement de base stationnaire instable.
Protas et Wesfreid (2002) avaient montré, a priori, que l'écoulement qui génêre le coefficient de trainée le plus faible pour une configuration donnée est l'écoulement de base stationnaire instable. Une preuve numérique prouvant la limite de ce résultat est publié ou un écoulement semblable à celui généré par le mouvement de la queue d'un poisson est obtenu,

Fig : Sillage de l'écoulement naturel, non contrôlé.

Fig : Sillage de l'écoulement de base stationnaire instable.
Protas et Wesfreid (2002) avaient montré, a priori, que l'écoulement qui génêre le coefficient de trainée le plus faible pour une configuration donnée est l'écoulement de base stationnaire instable. Une preuve numérique prouvant la limite de ce résultat est publié ou un écoulement semblable à celui généré par le mouvement de la queue d'un poisson est obtenu,
On the generation of a
reverse Von Karman street for the controlled cylinder
wake in the laminar regime
Bergmann M., Cordier L. & Brancher J.-P.
Phys. fluids 18 (2).
[Abstract] [http://] [pdf(452k)] [pdf©(530k)]
Bergmann M., Cordier L. & Brancher J.-P.
Phys. fluids 18 (2).
[Abstract] [http://] [pdf(452k)] [pdf©(530k)]

Fig : Sillage de l'écoulement pour
l'allée de Von Karman inversée.
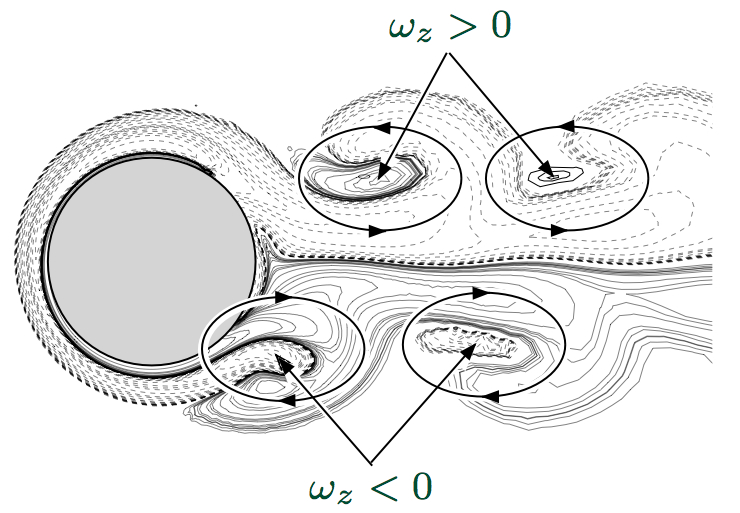
Fig : Zoom sur le sillage proche : allée
de Von Karman inversée.
Etude paramétrique
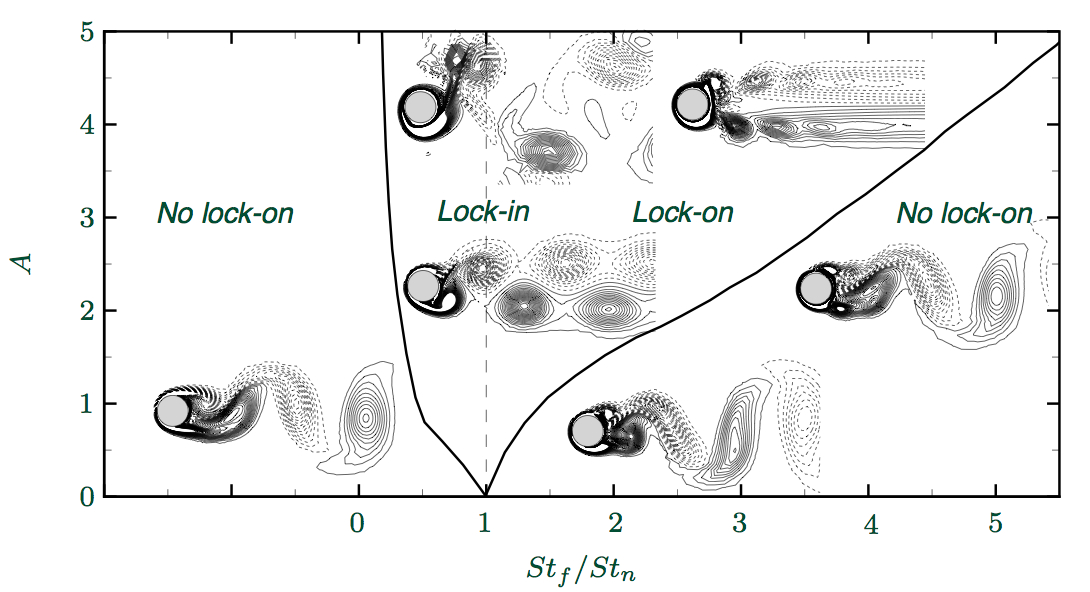
Dans un premier temps, une étude paramétrique a été effectuée afin de tester l'influence des paramêtres de contrôle sur l'écoulement, et plus précisément sur le coefficient de trainée moyen. Le coefficient de trainée moyen minimal vaut $0,993$ (soit un peu plus que celui de l'écoulement de base stationnaire instable, $C_D^{base}=0,94$) et est obtenu pour $A=4,25$ et $St_f=0,74$. On constate ensuite qu'il existe une valeur optimale pour l'angle de rotation $\Theta=A/\pi St_f$, qui permet de minimiser le coefficient de trainée moyen pour toutes les fréquences de forçage étudiées. Enfin, nous avons identifié des écoulements dits en lock-on pour lesquels la fréquence d'émission des tourbillons est égale à la fréquence de forçage. Ces résultats vont àªtre soumis pour publication à Physics of Fluids.
Dans la suite de cette étude, on souhaite déterminer des paramêtres de contrôle qui permettent de minimiser, tout au moins de réduire, la valeur du coefficient de trainée moyen, et ce, pour des coà»ts de calculs réduits. La théorie du contrôle optimal sera constamment utilisée.
La théorie du contrôle optimal
Le contrôle optimal est une méthode mathématique permettant de déterminer sans empirisme une loi de commande à partir de l'optimisation d'une fonctionnelle coà»t. Mathématiquement, tout problême de contrôle est défini par les quantités suivantes (Gunzburger, 1997) :
Il semble donc nécessaire de réduire l'ordre du modêle de résolution de l'écoulement. Pour ce faire, nous allons utiliser la décomposition Orthogonale aux valeurs Propres.
Réduction de modêle par Décomposition Orthogonale aux valeurs Propres
La décomposition orthogonale aux valeurs propres(POD, Proper Orthogonal Decomposition) tend à devenir d'une utilisation aussi courante que la décomposition de Fourier pour analyser des données issues de simulations numériques intensives ou d'expériences fines. En 2002, nous avons été sollicités par M. Riethmuller (Institut Von Karman, Belgique) et P. Millan (ONERA) pour donner deux cours\footnote{Suite au succês rencontré par ces cours, ils ont été donnés de nouveau en 2003.} sur la POD à l'Institut Von Karman. Dans le premier cours,
outre une présentation de la méthode des clichés introduite par Sirovich (1987) et de la méthode classique (Lumley, 1967), nous avons surtout insisté sur l'équivalence entre la POD et la décomposition aux valeurs singuliêres ou Singular Value Decomposition (SVD). Dans le second cours,
nous avons présenté deux applications typiques de la POD. La premiêre concerne l'extraction de structures cohérentes présentes au coeur d'une couche de mélange tridimensionnelle turbulente. Dans la seconde, nous avons considéré l'écoulement de sillage d'un cylindre circulaire en régime laminaire. Due à la rapidité de convergence énergétique de la POD, les fonctions propres POD ont par la suite été utilisées pour construire par projection de Galerkin sur les équations d'état, un systême dynamique permettant de représenter la dynamique non contrôlée de l'écoulement. Nous avons ensuite pris en compte la commande dans le modêle d'ordre réduit.
En comparant l'évolution temporelle des premiers coefficients obtenus par le modêle réduit (POD), à ceux obtenus directement par la simulation numérique (DNS), on constate, mis à part une légêre amplification, que les résultats sont en bon accord. Cette amplification est due à la troncature réalisée lors de la projection de Galerkin. Pour tenir compte des échelles dissipatives qui ne sont pas prises en compte de maniêre explicite dans le systême POD, nous avons développé une méthode de calcul de viscosité turbulente fonction du temps et du mode POD concerné. Cette méthode va àªtre soumise sur pour publication. En introduisant dans le systême dynamique POD la viscosité turbulente ainsi évaluée, il y a superposition exacte des dynamiques temporelles, d'une part, prédites par le systême dynamique d'ordre faible, et d'autre part, obtenues par simulation numérique. A cet instant, le modêle réduit de dynamique est capable de représenter parfaitement la dynamique, mais uniquement la dynamique utilisée pour générer les réalisations de l'écoulement. Il se pose alors naturellement la question du choix des réalisations en optimisation, au cours duquel les dynamiques sont susceptibles d'évoluer.
Choix des réalisations en optimisation
L'objectif est de représenter correctement le chemin d'optimisation menant d'une condition initiale à l'optimum désiré. La solution idéale serait d'obtenir des réalisations réparties le long du chemin d'optimisation. Pour répondre à ce problême, deux solutions ont été envisagées. La premiêre consiste à construire une base POD, dite généralisée, qui soit représentative d'une large gamme de dynamique. Ainsi, toutes les dynamiques le long du chemin d'optimisation peuvent àªtre considérées comme contenues dans cette base. La base POD ainsi construite ne sera pas réactualisée (voir Optimisation sans réactualisation de la base POD). Une seconde méthode consiste à considérer que la base POD ne représente qu'une dynamique particuliêre. On souhaite alors se déplacer pas à pas vers le minimum en réactualisant la base POD à chaque pas (voir Optimisation avec réactualisation de la base POD).
Optimisation sans réactualisation de la base POD
Afin de permettre au systême réduit POD de représenter l'ensemble des dynamiques intermédiaires intervenant pendant le processus d'optimisation, des fonctions de base POD généralisées ont été générées (Graham et al, 1999a). La méthode consiste à appliquer la POD à partir de données correspondant à l'écoulement de sillage subissant une excitation temporelle.La convergence énergétique est alors fortement dégradée et il est nécessaire de conserver plus de modes.
Ensuite, nous avons cherché à déterminer le contrôle optimal nécessaire pour réduire l'instationnarité de l'écoulement (Graham et al, 1999b). La méthode des multiplicateurs de Lagrange a été mise en oeuvre oû les équations d'état sont représentées par le systême réduit qui décrit la dynamique contrôlée de l'écoulement. Il a été trouvé une loi de contrôle harmonique $\gamma_{opt}(t)$ correspondant à une réduction relative de l'instationnarité égale à 70\%, avec $A=2,2$ et de fréquence $St_f=0,53$. Cette loi de commande permet d'obtenir une réduction relative de trainée de l'ordre de 25\%. L'écoulement a alors tendance à se symétriser pour tendre vers l'écoulement de base stationnaire instable. Mais cette loi de contrôle n'est pas optimale en ce qui concerne la minimisation du coefficient de trainée. Néanmoins, la réduction relative du coefficient de trainée obtenue est que três légêrement inférieure à celle trouvée dans des études similaires pour lesquelles les équations de Navier-Stokes sont utilisées comme équation d'état. De plus, nos coà»ts de calcul (CPU et mémoire) sont extràªmement réduits. En effet, le temps CPU nécessaire pour résoudre les équations réduites par POD représente, dans notre cas, 1\% du temps nécessaire pour résoudre les équations de Navier-Stokes. Par ailleurs, aprês calcul, la réduction du coà»t en mémoire est égale à 600 par rapport au cas oû les équations de Navier-Stokes seraient utilisées comme équations d'état.
Ces résultats ont fait l'objet de deux conférences nationales
Optimisation avec réactualisation de la base POD
Les modêles Galerkin-POD étant construits à partir de solutions des équations de Navier-Stokes correspondant à l'application d'un contrôle particulier, ils ont généralement un domaine de validité limité. Il parait donc inconcevable, exceptée la méthode présentée ci-dessus, de rechercher la solution d'un problême d'optimisation à l'aide de modêles réduits de dynamique à moins de les renouveler périodiquement au cours de la phase d'optimisation. Par conséquent, on voit apparaitre le besoin d'une méthode itérative dans laquelle la construction de modêles d'ordre faible successifs est couplée à la résolution du problême d'optimisation. On comprend aisément que le point crucial de la méthode est de déterminer le moment oà» il faut actualiser le modêle réduit de dynamique, celui-ci n'étant plus représentatif de la dynamique contrôlée.
Les méthodes à régions de confiance (Alexandrov et al, 1997) répondent complêtement à cette problématique. Nous pouvons suivre la qualité du modêle réduit de dynamique en comparant la performance des solutions du modêle réduit et du modêle précis. L'intéràªt des méthodes à régions de confiance est qu'elles permettent d'évaluer automatiquement le domaine de validité du modêle réduit de dynamique et de décider également de maniêre automatique l'actualisation d'un modêle qui ne serait plus représentatif. Occasionnellement, au cours du processus d'optimisation, on utilise des informations issues du modêle détaillé afin de recalibrer le modêle réduit. L'intéràªt de cette approche est qu'elle hérite des propriétés de convergence des méthodes à région de confiance. On est donc mathématiquement assuré que les itérés successifs du problême d'optimisation basé sur le modêle réduit, vont converger vers une solution d'optimisation locale du problême d'origine. Cette méthode dénommée TRPOD (Trust Region POD), présentée par Arian et al (2000) et Fahl (2000), semble àªtre la solution la plus prometteuse pour diminuer significativement le coà»t de calcul nécessaire à la résolution d'un problême de contrôle optimal.
Afin de tester la robustesse de la méthode d'optimisation couplant régions de confiance et modêles réduits POD, différentes conditions initiales ont été utilisées : le processus converge toujours vers les paramêtres de contrôle optimaux, $A=4,25$ et $St=0,74$. Ces convergences sont obtenues en moins de 8 résolutions du modêle de Navier-Stokes. Une réduction de trainée supérieure à 30\% est obtenue. L'écoulement contrôlé tend à se rapprocher de l'écoulement de base stationnaire instable.
Les coà»ts de calculs (CPU et mémoire) mis en jeu ont une nouvelle fois été considérablement réduits. En effet, le temps CPU nécessaire est réduit d'un facteur 4 par rapport à une méthode basée uniquement sur les équations de Navier-Stokes. Par ailleurs, on peut estimer la réduction du coà»t en mémoire à un ordre $1\,600$ par rapport au cas oà» les équations de Navier-Stokes seraient utilisées comme équations d'état, rendant en cela possible le contrôle optimal d'écoulements turbulents tridimensionnels ! Ces résultats ont été présentés dans le cadre d'une journée du GDR Contrôle des Décollements et aux
Enfin, une synthèse des ces méthodes d'optimisation basées sur la réduction de modêle a été présentée à la 1êre école de printemps "Optimisation et Contrôle des écoulements et des Transferts" organisée par le LIMSI-CNRS à Aussois, du 12 au 17 mars 2006.

Fig : Sillage correspondant à l'application de la loi de contrôle optimale.
Quid de le puissance de contrôle
Afin de développer toutes les techniques d'optimisation présentées, nous avons uniquement cherché à minimiser le coefficient de trainée, sans tenir compte de la puissance dépensée. Les contrôles obtenus ne sont a priori pas efficaces d'un point de vue énergétique. Une relation analytique donnant la puissance dépensée a alors été développée et a fait l'objet de la publication :
Dans un premier temps, une étude paramétrique a été effectuée afin de tester l'influence des paramêtres de contrôle sur l'écoulement, et plus précisément sur le coefficient de trainée moyen. Le coefficient de trainée moyen minimal vaut $0,993$ (soit un peu plus que celui de l'écoulement de base stationnaire instable, $C_D^{base}=0,94$) et est obtenu pour $A=4,25$ et $St_f=0,74$. On constate ensuite qu'il existe une valeur optimale pour l'angle de rotation $\Theta=A/\pi St_f$, qui permet de minimiser le coefficient de trainée moyen pour toutes les fréquences de forçage étudiées. Enfin, nous avons identifié des écoulements dits en lock-on pour lesquels la fréquence d'émission des tourbillons est égale à la fréquence de forçage. Ces résultats vont àªtre soumis pour publication à Physics of Fluids.

Fig :
visualisation de la zone de lock-on et quelques
écoulements typiques.
Dans la suite de cette étude, on souhaite déterminer des paramêtres de contrôle qui permettent de minimiser, tout au moins de réduire, la valeur du coefficient de trainée moyen, et ce, pour des coà»ts de calculs réduits. La théorie du contrôle optimal sera constamment utilisée.
La théorie du contrôle optimal
Le contrôle optimal est une méthode mathématique permettant de déterminer sans empirisme une loi de commande à partir de l'optimisation d'une fonctionnelle coà»t. Mathématiquement, tout problême de contrôle est défini par les quantités suivantes (Gunzburger, 1997) :
- Des variables d'état $\phi$ qui définissent les grandeurs caractéristiques du problême.
- Des paramêtres de contrôle $c$.
- Une fonctionnelle coà»t ou objectif ${\cal J}$} qui définit les objectifs que l'on souhaite atteindre.
- Des contraintes physiques} du problême, mathématiquement notées $F(\phi,\,c)=0$, qui traduisent l'évolution des variables d'état $\phi$ en fonction des paramêtres de contrôle $c$.
"without an inexpensive method for reducing the
cost of flow computations, it is unlikely that the
solution of optimization problems involving the three
dimensional unsteady Navier-Stokes system will become
routine".
Il semble donc nécessaire de réduire l'ordre du modêle de résolution de l'écoulement. Pour ce faire, nous allons utiliser la décomposition Orthogonale aux valeurs Propres.
Réduction de modêle par Décomposition Orthogonale aux valeurs Propres
La décomposition orthogonale aux valeurs propres(POD, Proper Orthogonal Decomposition) tend à devenir d'une utilisation aussi courante que la décomposition de Fourier pour analyser des données issues de simulations numériques intensives ou d'expériences fines. En 2002, nous avons été sollicités par M. Riethmuller (Institut Von Karman, Belgique) et P. Millan (ONERA) pour donner deux cours\footnote{Suite au succês rencontré par ces cours, ils ont été donnés de nouveau en 2003.} sur la POD à l'Institut Von Karman. Dans le premier cours,
Proper Orthogonal Decomposition: an overview
Cordier L. & Bergmann M.
Lecture series 2002-04 and 2003-04 on post-processing of experimental and numerical data, Von Karman Institute for Fluid Dynamics, 46 pages.
[pdf(870k)]
Cordier L. & Bergmann M.
Lecture series 2002-04 and 2003-04 on post-processing of experimental and numerical data, Von Karman Institute for Fluid Dynamics, 46 pages.
[pdf(870k)]
outre une présentation de la méthode des clichés introduite par Sirovich (1987) et de la méthode classique (Lumley, 1967), nous avons surtout insisté sur l'équivalence entre la POD et la décomposition aux valeurs singuliêres ou Singular Value Decomposition (SVD). Dans le second cours,
Two typical applications of POD: coherent
structures eduction and reduced order modelling
Cordier L. & Bergmann M.
Lecture series 2002-04 and 2003-04 on post-processing of experimental and numerical data, Von Karman Institute for Fluid Dynamics, 60 pages.
[pdf(3.5Mo)]
Cordier L. & Bergmann M.
Lecture series 2002-04 and 2003-04 on post-processing of experimental and numerical data, Von Karman Institute for Fluid Dynamics, 60 pages.
[pdf(3.5Mo)]
nous avons présenté deux applications typiques de la POD. La premiêre concerne l'extraction de structures cohérentes présentes au coeur d'une couche de mélange tridimensionnelle turbulente. Dans la seconde, nous avons considéré l'écoulement de sillage d'un cylindre circulaire en régime laminaire. Due à la rapidité de convergence énergétique de la POD, les fonctions propres POD ont par la suite été utilisées pour construire par projection de Galerkin sur les équations d'état, un systême dynamique permettant de représenter la dynamique non contrôlée de l'écoulement. Nous avons ensuite pris en compte la commande dans le modêle d'ordre réduit.
En comparant l'évolution temporelle des premiers coefficients obtenus par le modêle réduit (POD), à ceux obtenus directement par la simulation numérique (DNS), on constate, mis à part une légêre amplification, que les résultats sont en bon accord. Cette amplification est due à la troncature réalisée lors de la projection de Galerkin. Pour tenir compte des échelles dissipatives qui ne sont pas prises en compte de maniêre explicite dans le systême POD, nous avons développé une méthode de calcul de viscosité turbulente fonction du temps et du mode POD concerné. Cette méthode va àªtre soumise sur pour publication. En introduisant dans le systême dynamique POD la viscosité turbulente ainsi évaluée, il y a superposition exacte des dynamiques temporelles, d'une part, prédites par le systême dynamique d'ordre faible, et d'autre part, obtenues par simulation numérique. A cet instant, le modêle réduit de dynamique est capable de représenter parfaitement la dynamique, mais uniquement la dynamique utilisée pour générer les réalisations de l'écoulement. Il se pose alors naturellement la question du choix des réalisations en optimisation, au cours duquel les dynamiques sont susceptibles d'évoluer.
Choix des réalisations en optimisation
L'objectif est de représenter correctement le chemin d'optimisation menant d'une condition initiale à l'optimum désiré. La solution idéale serait d'obtenir des réalisations réparties le long du chemin d'optimisation. Pour répondre à ce problême, deux solutions ont été envisagées. La premiêre consiste à construire une base POD, dite généralisée, qui soit représentative d'une large gamme de dynamique. Ainsi, toutes les dynamiques le long du chemin d'optimisation peuvent àªtre considérées comme contenues dans cette base. La base POD ainsi construite ne sera pas réactualisée (voir Optimisation sans réactualisation de la base POD). Une seconde méthode consiste à considérer que la base POD ne représente qu'une dynamique particuliêre. On souhaite alors se déplacer pas à pas vers le minimum en réactualisant la base POD à chaque pas (voir Optimisation avec réactualisation de la base POD).
Optimisation sans réactualisation de la base POD
Afin de permettre au systême réduit POD de représenter l'ensemble des dynamiques intermédiaires intervenant pendant le processus d'optimisation, des fonctions de base POD généralisées ont été générées (Graham et al, 1999a). La méthode consiste à appliquer la POD à partir de données correspondant à l'écoulement de sillage subissant une excitation temporelle.La convergence énergétique est alors fortement dégradée et il est nécessaire de conserver plus de modes.
Ensuite, nous avons cherché à déterminer le contrôle optimal nécessaire pour réduire l'instationnarité de l'écoulement (Graham et al, 1999b). La méthode des multiplicateurs de Lagrange a été mise en oeuvre oû les équations d'état sont représentées par le systême réduit qui décrit la dynamique contrôlée de l'écoulement. Il a été trouvé une loi de contrôle harmonique $\gamma_{opt}(t)$ correspondant à une réduction relative de l'instationnarité égale à 70\%, avec $A=2,2$ et de fréquence $St_f=0,53$. Cette loi de commande permet d'obtenir une réduction relative de trainée de l'ordre de 25\%. L'écoulement a alors tendance à se symétriser pour tendre vers l'écoulement de base stationnaire instable. Mais cette loi de contrôle n'est pas optimale en ce qui concerne la minimisation du coefficient de trainée. Néanmoins, la réduction relative du coefficient de trainée obtenue est que três légêrement inférieure à celle trouvée dans des études similaires pour lesquelles les équations de Navier-Stokes sont utilisées comme équation d'état. De plus, nos coà»ts de calcul (CPU et mémoire) sont extràªmement réduits. En effet, le temps CPU nécessaire pour résoudre les équations réduites par POD représente, dans notre cas, 1\% du temps nécessaire pour résoudre les équations de Navier-Stokes. Par ailleurs, aprês calcul, la réduction du coà»t en mémoire est égale à 600 par rapport au cas oû les équations de Navier-Stokes seraient utilisées comme équations d'état.
Ces résultats ont fait l'objet de deux conférences nationales
- 16ême Congrês Français de
Mécanique, Nice, 1-5 septembre 2003,
- 39ême Colloque d'Aérodynamique Appliquée, AAAF, Paris, mars 2004
et de quatre conférences à audience internationale- 39ême Colloque d'Aérodynamique Appliquée, AAAF, Paris, mars 2004
- 56th Annual APS/DFD
Meeting, New-York, USA, décembre 2003,
- 3rd European Drag Reduction Meeting, Aussois, France, 1-4 June 2004,
- 2nd AIAA Flow Control Conference, Portland, USA, juin 2004.
- 1stEuropean Forum on Flow Control, Poitiers, France, octobre 2004.
Par ailleurs, ils ont été publiés dans la revue Physics of Fluids,- 3rd European Drag Reduction Meeting, Aussois, France, 1-4 June 2004,
- 2nd AIAA Flow Control Conference, Portland, USA, juin 2004.
- 1stEuropean Forum on Flow Control, Poitiers, France, octobre 2004.
Optimal rotary control of the cylinder wake using
POD reduced order model
Bergmann M., Cordier L. & Brancher J.-P.
Phys. fluids 17 (9).
[Abstract] [http://] [pdf(1.8Mo)] [pdf©(5.2Mo)]
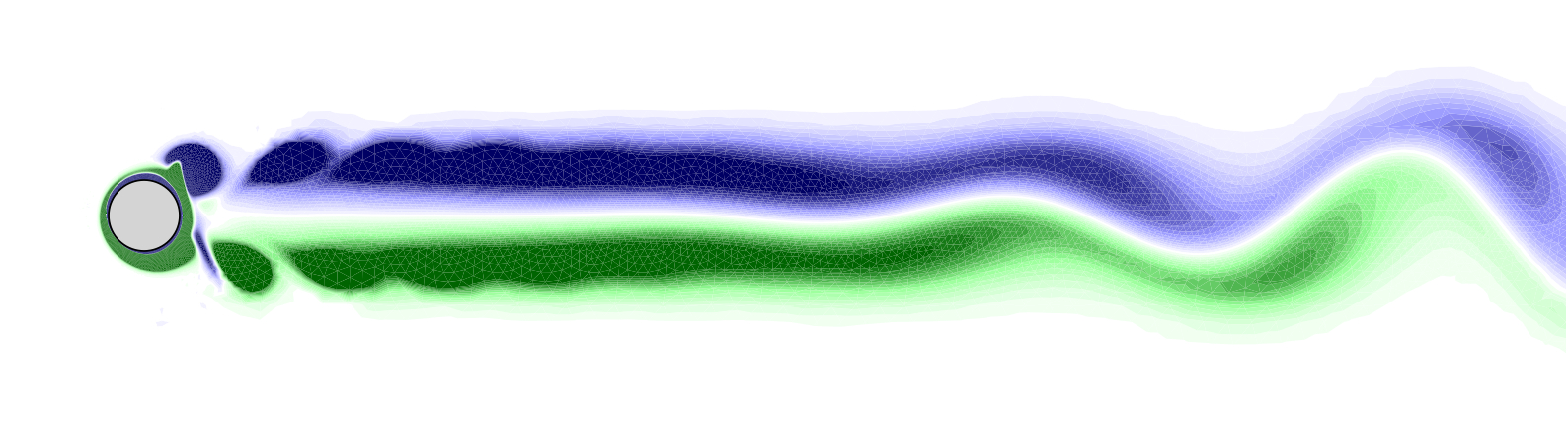
Fig : Sillage correspondant à l'application de la loi de contrôle sous-optimale.
Bergmann M., Cordier L. & Brancher J.-P.
Phys. fluids 17 (9).
[Abstract] [http://] [pdf(1.8Mo)] [pdf©(5.2Mo)]

Fig : Sillage correspondant à l'application de la loi de contrôle sous-optimale.
Optimisation avec réactualisation de la base POD
Les modêles Galerkin-POD étant construits à partir de solutions des équations de Navier-Stokes correspondant à l'application d'un contrôle particulier, ils ont généralement un domaine de validité limité. Il parait donc inconcevable, exceptée la méthode présentée ci-dessus, de rechercher la solution d'un problême d'optimisation à l'aide de modêles réduits de dynamique à moins de les renouveler périodiquement au cours de la phase d'optimisation. Par conséquent, on voit apparaitre le besoin d'une méthode itérative dans laquelle la construction de modêles d'ordre faible successifs est couplée à la résolution du problême d'optimisation. On comprend aisément que le point crucial de la méthode est de déterminer le moment oà» il faut actualiser le modêle réduit de dynamique, celui-ci n'étant plus représentatif de la dynamique contrôlée.
Les méthodes à régions de confiance (Alexandrov et al, 1997) répondent complêtement à cette problématique. Nous pouvons suivre la qualité du modêle réduit de dynamique en comparant la performance des solutions du modêle réduit et du modêle précis. L'intéràªt des méthodes à régions de confiance est qu'elles permettent d'évaluer automatiquement le domaine de validité du modêle réduit de dynamique et de décider également de maniêre automatique l'actualisation d'un modêle qui ne serait plus représentatif. Occasionnellement, au cours du processus d'optimisation, on utilise des informations issues du modêle détaillé afin de recalibrer le modêle réduit. L'intéràªt de cette approche est qu'elle hérite des propriétés de convergence des méthodes à région de confiance. On est donc mathématiquement assuré que les itérés successifs du problême d'optimisation basé sur le modêle réduit, vont converger vers une solution d'optimisation locale du problême d'origine. Cette méthode dénommée TRPOD (Trust Region POD), présentée par Arian et al (2000) et Fahl (2000), semble àªtre la solution la plus prometteuse pour diminuer significativement le coà»t de calcul nécessaire à la résolution d'un problême de contrôle optimal.
Afin de tester la robustesse de la méthode d'optimisation couplant régions de confiance et modêles réduits POD, différentes conditions initiales ont été utilisées : le processus converge toujours vers les paramêtres de contrôle optimaux, $A=4,25$ et $St=0,74$. Ces convergences sont obtenues en moins de 8 résolutions du modêle de Navier-Stokes. Une réduction de trainée supérieure à 30\% est obtenue. L'écoulement contrôlé tend à se rapprocher de l'écoulement de base stationnaire instable.
Les coà»ts de calculs (CPU et mémoire) mis en jeu ont une nouvelle fois été considérablement réduits. En effet, le temps CPU nécessaire est réduit d'un facteur 4 par rapport à une méthode basée uniquement sur les équations de Navier-Stokes. Par ailleurs, on peut estimer la réduction du coà»t en mémoire à un ordre $1\,600$ par rapport au cas oà» les équations de Navier-Stokes seraient utilisées comme équations d'état, rendant en cela possible le contrôle optimal d'écoulements turbulents tridimensionnels ! Ces résultats ont été présentés dans le cadre d'une journée du GDR Contrôle des Décollements et aux
- 17ême Congrês Français de
Mécanique, Troyes, septembre 2005, participation invitée,
conférence d'ouverture.
- 58th Annual APS/DFD Meeting, Chicago, USA, décembre 2005, sur invitation de D. Rempfer (IIT Chicago) et B.R. Noack (TU Berlin).
- 44th IEEE Conference on Decision and Control and European Control Conference ECC 2005, Séville, Espagne, décembre 2005}, sur invitation de G. Tadmor (Boston University) et C. Rowley (Princeton University).
- 3rd AIAA Flow Control Conference, San Francisco, USA, juin 2006.
De plus, ces résultats sont soumis à Journal of Fluid Mechanics,- 58th Annual APS/DFD Meeting, Chicago, USA, décembre 2005, sur invitation de D. Rempfer (IIT Chicago) et B.R. Noack (TU Berlin).
- 44th IEEE Conference on Decision and Control and European Control Conference ECC 2005, Séville, Espagne, décembre 2005}, sur invitation de G. Tadmor (Boston University) et C. Rowley (Princeton University).
- 3rd AIAA Flow Control Conference, San Francisco, USA, juin 2006.
Control of the cylinder wake in the laminar
regime by adaptive methods based on POD Reduced Order
Models.
Bergmann M., Cordier L. & Brancher J.-P.
J. Comput. Physics, under review
[Abstract] [pdf(6.2Mo)]
Bergmann M., Cordier L. & Brancher J.-P.
J. Comput. Physics, under review
[Abstract] [pdf(6.2Mo)]
Enfin, une synthèse des ces méthodes d'optimisation basées sur la réduction de modêle a été présentée à la 1êre école de printemps "Optimisation et Contrôle des écoulements et des Transferts" organisée par le LIMSI-CNRS à Aussois, du 12 au 17 mars 2006.

Fig : Sillage correspondant à l'application de la loi de contrôle optimale.
Quid de le puissance de contrôle
Afin de développer toutes les techniques d'optimisation présentées, nous avons uniquement cherché à minimiser le coefficient de trainée, sans tenir compte de la puissance dépensée. Les contrôles obtenus ne sont a priori pas efficaces d'un point de vue énergétique. Une relation analytique donnant la puissance dépensée a alors été développée et a fait l'objet de la publication :
On the power used to control the circular
cylinder drag
Bergmann M., Cordier L. & Brancher J.-P.
Phys. fluids 18 (8).
[Abstract] [http://] [pdf(135k)] [pdf©(160k)]
Bergmann M., Cordier L. & Brancher J.-P.
Phys. fluids 18 (8).
[Abstract] [http://] [pdf(135k)] [pdf©(160k)]
La puissance dépensée évolue
avec le carré de l'amplitude de forcage et avec la racine
carrée du nombre de Strouhal de forcage. Il est enfin
montré qu'il est possible d'obtenir un contrôle efficace
pour de faibles valeurs de l'amplitude des oscillations du
cylindre ($A=0,1$, $St_f=0,05$).
Activités de recherche réalisées en post-doctorat au LEMTA [home] [top]
Mon stage post-doctoral financé par le CNRS concernait la modélisation des systêmes complexes et s'est déroulé dans l'équipe feux de forêts animée par Olivier Séro-Guillaume, directeur de recherches CNRS au LEMTA. Ce stage m'a permis d'utiliser mes connaissances en modélisation et contrôle pour les appliquer dans les systêmes de réaction diffusion, et plus particuliêrement à la modélisation des feux de forts et à la lutte.

Fig : Simulation de la propagation d'un feu de fort
L'équipe feux de forêt a développé un modèle de type réaction diffusion pour la propagation des feux de forêts. Certains termes présents dans le code de calcul associé sont extrêtmement coûteux à évaluer en temps de calcul. La première étape de mon travail consistait donc à optimiser ce code. Ces termes "coûteux" sont évalués par des réseaux de neurones. La construction d'un réseau de neurone consiste à déterminer les poids et les biais les plus adaptés pour représenter au mieux un jeu de données à "apprendre". J'ai de ce fait développé deux types de réseaux de neurones. Le premier, assez classique, est basé sur des méthodes de descente (gradient conjugué, BFGS, etc). Le second consiste à déterminer les poids et les biais à l'aide d'un algorithme génétique. L'utilisation de ces réseaux de neurones permet alors de réduire les coûts de calcul d'un facteur supérieur à 200, et ce, pour une précision supérieur à 1\%.
Ensuite, mon travail consistait, à partir de quelques mesures du front d'un feu, à déterminer l'origine (en espace et en temps) de départ de ce feu. étant donné que la propagation des feux de forêts est composée de phénomènes qui sont fortement irréversibles (il est impossible d'intégrer le modèle en temps rétrograde), ce problème, qui peut par exemple être très intéressant d'un point de vue d'expertises pour les assurances, est alors formulé comme un problème d'optimisation : déterminer l'origine spatio-temporel du feu qui minimise l'écart entre la ligne de feu issue de ce point et la ligne correspondant au feu étudié ? Ce problème est résolu en couplant une méthode de simplexe avec une méthode classique de gradient conjugué. Ce travail a fait l'objet de la publication suivante :
Note on the determination of the ignition point
in forest fires propagation using a control algorithm
Bergmann M., Ramezani S. & Séro-Guillaume O.
Commun. Numer. Meth. Engng., article online in advance of print
[Abstract] [http://] [pdf(400k)] [pdf©(316k)]
Bergmann M., Ramezani S. & Séro-Guillaume O.
Commun. Numer. Meth. Engng., article online in advance of print
[Abstract] [http://] [pdf(400k)] [pdf©(316k)]
Enfin, la dernière partie de ce stage post-doctoral consistait à déterminer précisément la position du front d'un feu. En effet, en raison des denses fumées relachées durant un feu de forêt, il est actuellement très délicat d'évaluer réellement et de façon précise cette position. étant donné que beaucoup de paramètres du modèle mathématique de propagation ont une valeur mal connue, la connaissance de la position exacte du front du feu (déterminée expérimentalement) permettra de calibrer le modèle (assimilation de donnée). Le front d'un feu est généralement déterminé par une température (fixe). Pour déterminer cette température il serait nécessaire d'utiliser un très grand nombre de thermocouples. Dans cette étude, on choisit d'évaluer la position par une méthode inverse utilisant des mesures de flux de chaleur. La méthode suivie consiste donc à résoudre un problème d'optimisation. Tout d'abord, il est nécessaire, avec un nombre de capteurs donné, d'approcher le mieux possible le front du feu calculé de celui obtenu expérimentalement. Ensuite, d'un point de vue plus économique, il était intéressant de minimiser le nombre de capteurs nécessaires à la bonne reconstruction du front du feu. Ces travaux ont été soumis pour publication dans la revue Inverse Problems :
On the estimation of the forest fire front
position
Bergmann M., Séro-Guillaume O. & Ramezani S.
Inverse problems, under review
[Abstract] [pdf(250k)]
Bergmann M., Séro-Guillaume O. & Ramezani S.
Inverse problems, under review
[Abstract] [pdf(250k)]
Mon stage post-doctoral est financé par l'INRIA Futurs et se déroule au sein de l'équipe MC2 (Modélisation, Calcul et Contrôle) au Laboratoire de Mathématiques Appliquées de Bordeaux (MAB) sous la supervision des Professeurs A. Iollo et C.-H. Bruneau. Ce stage concerne l'amélioration de la représentativité dynamique des bases globales construites par POD.
Comme il a été démontré dans ma thèse, un modèle réduit de dynamique construit par POD représente uniquement la dynamique utilisée pour générer les réalisations de l'écoulement. Ainsi, un modèle réduit construit à partir de réalisations qui correspondent à une dynamique donnée n'a a priori aucune garantie de représenter fidèlement une autre dynamique a fortiori si celle-ci est très éloignée de la première). Des évolutions dynamiques peuvent en particulier intervenir lors de variations de paramètres du système (nombre de Reynolds, paramètres de contrôle, etc). Nous considérons ici uniquement des variations du nombre de Reynolds. Afin de rendre un modèle réduit POD plus robuste envers les évolutions dynamiques, il est nécessaire d'améliorer la base POD elle-mêtme. A cet effet, il semble intéressant d'évaluer "ce qu'il manque" à une base POD construite à un nombre de Reynolds pour représenter plus finement une dynamique correspondant à autre nombre de Reynolds. L'approche suivie est alors basée sur l'évaluation du résidu ${\cal R}(\bm{U},\,Re)$ des équations de Navier-Stokes ($\bm{U}=(u,\,v,\,p)^T$). L'algorithme est le suivant : on construit une base POD $\bm{\Phi}_{Re_1}$ qui correspond à un nombre de Reynolds $Re_1$, on reconstruit l'écoulement $\bm{U}=\sum_{i=1}^{N} a^{(i)}(t)\bm{\Phi}^{(i)}_{Re_1}(\bm{x})$ ($N$ représente le nombre de modes propres retenus), puis on évalue le résidu de l'opérateur de Navier-Stokes pour un autre nombre de Reynolds ${\cal R}(\{a^{(i)}\}_{i=1}^N,\,\{\bm{\Phi}^{(i)}_{Re_1}\} _{i=1}^N,\, Re_2)$. Les coefficients $\{a^{(i)}(t)\}_{i=1}^N$ peuvent être calculés de façon classique en résolvant un système dynamique réduit (modèle POD) construit pour le nombre de Reynolds $Re_1$. Mais dans ce cas rien n'assure que ce jeu de coefficients $\{a^{(i)}\}$ soit le plus adapté pour représenter au mieux les champs pour le nombre de Reynolds $Re_2$. Une façon plus intelligente consiste alors à déterminer ces coefficients par une méthode de Galerkin non-linéaire (Marion et Temam, 1989 ; Ma, 2001) par minimisation du résidu sur l'espace engendré par les vecteurs propres $\{\bm{\Phi}^{(i)}_{Re_1}\}_{i=1}^N$. Outre le fait qu'il ne soit plus nécessaire de construire et de résoudre un système réduit, un des avantages de cette méthode est qu'il n'est plus nécessaire de modéliser les interactions avec les modes non-résolus par le système réduit, ce qui est souvent assez coûteux numériquement. A cet instant le résidu des équations de Navier-Stokes peut être calculé, et sa valeur nous fournit alors une estimation de la quantité d'information à rajouter à la base POD. La question est alors : "quels modes faut-il rajouter à la base POD ?".
La première idée a été de décomposer un ensemble de réalisations des résidus en modes propres POD, puis d'ajouter ces modes à la base existante en utilisant une procédure d'orthonormalisation de \textbf{Gram-Schmidt} afin de conserver les propriétés de la base POD. Malheureusement, la base des résidus n'est pas à divergence nulle. Cette base peut alors être projetée dans un sous espace à divergence nulle, mais la pression ne peut hélas plus être actualisée. Cette méthode permet d'améliorer la représentativité de la base POD, mais assez loin de nos espérances. Une seconde méthode est donc mise en oeuvre.
Cette fois-ci, la méthode consiste à compléter la base POD existante à l'aide d'une méthode GMRES (Generalized Minimal Residual, Saad et Schultz, 1986) en itérant dans des sous-espaces de Krylov construits sur le résidu de l'opérateur de Navier-Stokes (Ryckelynk, 2002 et 2005). La procédure est la suivante : on part d'une base existante pour un nombre de Reynolds $Re_1$, on reconstruit l'écoulement $\bm{U}=\sum_{i=1}^{N} a^{(i)}(t)\bm{\Phi}^{(i)}_{Re_1}(\bm{x})$ , puis on évalue le résidu ${\cal R}(\bm{U},\, Re_2)$. Tant que ce résidu est jugé suffisamment faible, la base demeure inchangée, et on progresse dans le temps par incrémentation des coefficients $a^{(i)}(t)$. Sinon, on cherche sur l'espace de Krylov engendré par ce résidu le mode qui minimise le nouveau résidu. Ce mode est ensuite ajouté à la base pré-existante par un méthode de Gram-Schmidt. La base va ainsi être actualisée au fur et à mesure que l'on progresse en temps, jusqu'à converger vers la base "optimale".
L'avantage de cette méthode est que la base POD est construite a priori (i.e. on ne résout plus les équations de Navier-Stokes). Ainsi, cette méthode est assez peu coûteuse en temps CPU et permettra de construire une base POD représentative de tout un ensemble de dynamiques. Cette base sera utilisée in fine dans une procédure de contrôle optimal suivant la méthode TRPOD développée dans le cadre de ma thèse.
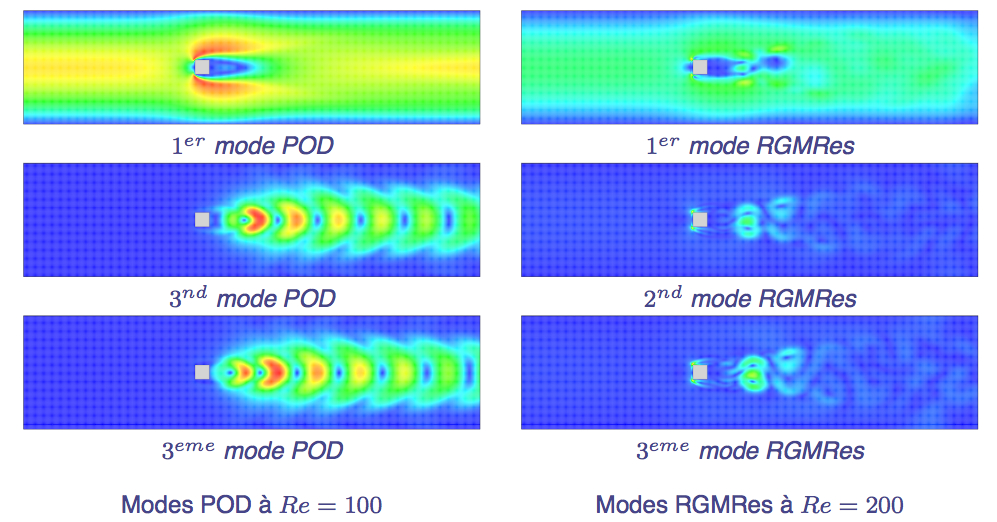
Fig : Visualisation de la norme des modes propres POD et RGMRES.
N. Alexandrov, J.E. Dennis Jr, R.M. Lewis et V. Torczon A Trust Region framework for managing the use of approximation models in optimization. Icase report, 97-50, 1997.
E. Arian, M. Fahl et E.W. Sachs Trust-Region Proper Orthogonal Decomposition for Flow Control. Icase report, 2000-25, 2000.
A.J. Chorin Numerical solution of the Navier-Stokes equations. Math. Comp., 22:745-762, 1968.
M. Fahl Trust-Region methods for flow control based on Reduced Order Modeling. Thèse de doctorat, université de Trier, 2000.
M. Gad-el-Hak Flow Control: Passive, Active and Reactive Flow Management. Cambridge University Press, London, United Kingdom, 2000.
W.R. Graham, J. Peraire et K.T. Tang Optimal Control of Vortex Shedding Using Low Order Models. Part 1. Open-Loop Model Development. Int. J. for Numer. Meth. in Engrg., 44(7):945-972, 1999a.
W.R. Graham, J. Peraire et K.T. Tang Optimal Control of Vortex Shedding Using Low Order Models. Part 2: Model-based control. Int. J. for Numer. Meth. in Engrg., 44(7):973-990, 1999b.
M.D. Gunzburger Introduction into mathematical aspects of flow control and optimization. In Lecture series 1997-05 on inverse design and optimization methods. Von Karman Institute for Fluid Dynamics, 1997.
M.D. Gunzburger Adjoint Equation-Based Methods for Control Problems in Incompressible, Viscous Flows. Flow, Turbulence and Combustion, 65:249-272, 2000.
G. Jin et M. Braza A Nonreflecting Outlet Boundary Condition for Incompressible Unsteady Navier-Stokes Calculations. J. Comp. Phys., 107(2):239-253, 1993.
J.L. Lumley Atmospheric Turbulence and Wave Propagation. The structure of inhomogeneous turbulence, pages 166-178. A.M. Yaglom & V.I. Tatarski, 1967.
X. Ma Hierarchical Galerkin and non-linear Galerkin models for laminar and turbulent wakes. PhD thesis, Division of Applied Mathematics, Brown University, 2001.
M. Marion et R. Temam Nonlinear Galerkin methods. SIAM J. Numer. Anal., 26(5):1139–1157, 1989.
L. Prandtl The mechanics of viscous fluids. Durand., 1935.
B. Protas et J.E. Wesfreid Drag force in the open-loop control of the cylinder wake in the laminar regime. Phys. Fluids, 14(2):810-826, 2002.
D. Ryckelynck Réduction a priori de modèles thermomécaniques. C.R. Mecaniques 330:499-505, 2002.
D. Ryckelynck A priori hyperreduction method: an adaptative approach Journal of Comput. Physics, 202:346-366, 2005.
Y. Saad et Schultz M.H. GMRES : A generalized residual algorithm for solving nonsymetric linear systems SIAM J. Sci. Stat. Comput., 7(3):856-869, 1986
L. Sirovich Turbulence and the dynamics of coherent structures. Part 1: Coherent structures. Quarterly of Applied Mathematics, XLV(3):561-571, 1987.