• Introduction
  • Installation
  • Overview
  • Compilation
  • Data file
• Algebra
• Quadrature
• Common functions
• Mesh
• Finite Elements
• Computations
• Boundary conditions
• Post-processing
• Solved equations
• Time schemes

Overview

Montjoie is a high-order finite element C++ framework, to solve time-domain or time-harmonic linear partial differential equations. There are several finite element : nodal finite elements, discontinuous Galerkin finite elements, edge finite elements. Two- and threedimensional computational domains are supported. The quadrilateral/hexahedral finite elements are described in [Cohen, 2002], [Duruflé, 2006]. The triangular/tetrahedral elements can be classically found in the litterature. Montjoie handles conformal meshes (no hanging nodes) hexahedral dominant. The finite elements used for triangular prisms and pyramids are detailed in Morgane Bergot's thesis. In this manuscript the case of tetrahedra and hexhedra is also treated. Isoparametric curved elements are available, in order to have a good approximation of the geometry. Classical curved surfaces are available in 3-D (spheres, cylinders or cones), and also high-order mesh files (Exodus and Gmsh format). In 2-D, there are classical curves and also approximation of curves by splines. The equations currently solved by the code are mainly linear and simulate wave propagation : Helmholtz equation (and wave equation), Maxwell's equations, Aeroacoustics (linearized euler equations), Elastodynamics (as well as Reissner-Mindlin model and fluid-structure interaction). The physical properties can be constant on each element, or they can vary. The variation of a physical index is given by values on a regular grid, or on a mesh. The mesh where the index is defined can be different from the computational mesh. An interpolation is then performed.

If you are using Montjoie, you should avoid specifying a first-order approximation in space (P1, Q1). Montjoie is not optimized for first-order approximation, for example it will store all the edges and faces with connectivity (so that, for each element, you know the face numbers and edge numbers). Of course, such informations require a lot of storage when first order is used, whereas it becomes negligible compared to other quantities to store in case of high order scheme.

The boundary conditions are classical : Dirichlet, Neumann, Robin, absorbing. The code provides also boundary conditions for bodies with a high conductivity (for Helmholtz equation). PML layers are implemented for several equations. In time-domain computations, there can be some instabilities (mainly for elastodynamic equation). A transparent condition (using integral representation formula) is also available for Helmholtz and Maxwell's equations.

How to get started

First, you will need to compile the code for a given set of equations. For example, if you want to solve 3-D acoustics equation, you can type :

$ make acous3D

For an exhaustive list of compilation targets (and associated compiled files), you can take a look at this section. When you run the code, you put the data file in the command line :

$ ./acous3D.x time_sphere.ini

The data files have the ini extension, for simplicity purpose. This extension is not required. The name of the executable is not necessarily acous3D.x, it can be helmholtz2D.x, maxwell3D.x ... It depends on the solved equation, and on the target selected by the user during the compilation. For a detailed description of the data file format, you can read this section

.

Hierarchy of directories

When you clone the repository with Git (or by uncompressing a tar.gz file), the two following directories are created :

• SELDON : directory containing a compatible version of Seldon for this release of Montjoie.
• MONTJOIE : directory containing Montjoie

The Seldon files contained in Montjoie are not different from the official version of Seldon, but since Seldon library is sometimes evolving, we always ensure that Montjoie is compatible with the version contained in the folder SELDON. Hence, when you revert to a release of Montjoie, you have always a compatible version of Seldon library. The Montjoie software is contained in directory MONTJOIE with the following structure :

• src : C++ source files (the library Montjoie)
• MAILLAGES : the meshes used by non-regression tests (examples)
• MATLAB : some Python/Matlab scripts useful to read vectors, matrices, and output files generated by Montjoie.
• cluster : some scripts (e.g. Python scripts to launch non-regression tests)
• example : non-regression tests
• lib : this directory will contain compiled files (extension .o or .a)
• post : some scripts for post-processing

The source files contained in src directory are organized in the following directories

• Algebra : "Seldon-like" functions related to vectors and matrices.
• Computation : files containing the functions for computing elementary matrices, and assemble them. It also contains matrix-vector products (when the matrix is not stored).
• Corde : files associated with the motion of strings in a piano
• Elliptic : files containing the definition of time-harmonic equations (or stationary equations)
• FiniteElement : finite element classes
• Harmonic : General functions for time-harmonic problems
• Hyperbolic : files containing the definition of time-dependent equations
• Instationary : General functions for time-dependent problems
• Mesh : functions and classes associated with the treatment of meshes
• Output : post-processing functions
• Program : files with the "main" function, which are compiled
• Regularization : regularized iterative methods for solving non-linear least squares problems (used for inverse problems)
• Quadrature : Gauss-Jacobi quadrature formulas over unit interval, and quadrature rules over square, triangle, tetrahedron, pyramid, prism and cube.
• Share : various functions and classes
• Solver : files related to the solution of linear systems and eigenvalue problems.
• Source : different availables sources in Montjoie

The directory Program contains the codes solving different equations by using Montjoie library, whereas all the other directories are containing the library.

General structure of the code

The functions contained in directory Share and Algebra are independent and complete Seldon library. The functions and classes contained in Quadrature can be used if you need quadrature formulas over the unit interval, unit triangle, square, tetrahedron, symmetric pyramid, unit triangular prism, and unit cube. The classes contained in FiniteElement are defining the different finite elements available in the library. The base classes TriangleGeomReference, QuadrangleGeomReference, TetrahedronGeomReference, PyramidGeomReference, WedgeGeomReference and HexahedronGeomReference are actually used in class Mesh for handling high order curved mesh. If you wish to use only the mesh structure in Montjoie, you can include "MontjoieMesh.hxx" instead of "Montjoie.hxx".

The general functions for solving stationary equations are contained in Computation, Harmonic, Source and Output. The general functions for handling time-dependent problems (i.e. time-schemes and treatment of mass matrix) are contained in Instationary. Specific time-harmonic equations currently solved by Montjoie (Helmholtz, Maxwell, aeroacoustic and elastodynamic) are implemented in the directory Elliptic, where unsteady equations are implemented in the directory Hyperbolic. These specific equations are not included by default, but you include them if needed as it will be explained further.

In order to perform the solution of a partial differential equation with a finite element method, we need to know :

• The equation solved within its variational formulation. The way to describe an equation in Montjoie is detailed in the section devoted to solved equations. The files containing default equations solved in Montjoie are placed in directory src/Elliptic for time-harmonic and stationary equations (ultimately equations not depending on time), and in directory src/Hyperbolic for time-dependent equations. Usually the solution of a time-dependent problem relies on the description of the associated stationary problem (by replacing derivatives in time by coefficients). The solved equation constitutes a template parameter (often named TypeEquation) of fundamental classes EllipticProblem and HyperbolicProblem.
• The finite element used, i.e. quadrilateral with Gauss-Lobatto points, triangle with Lagrange interpolatory functions, tetrahedron with hierarchical functions, pyramid with hierarchical edge functions... All the finite element classes are contained in directory src/FiniteElement. The finite element constitutes a template parameter (often named TypeElement) of fundamental classes EllipticProblem and HyperbolicProblem.

Class EllipticProblem contains the mesh (attribute mesh), the finite element objects (accessed through GetReferenceElement method), the parameters of data file (for example, frequency, boundary conditions, name of outputfiles, etc), arrays containing geometric datas (like jacobian matrices on each element), and useful member functions (such as computing the finite element matrix, computing the right hand sides, writing solution in output files). So an object EllipticProblem contains all what is necessary to perform a computation. The inheritance diagramm of EllipticProblem is detailed below :

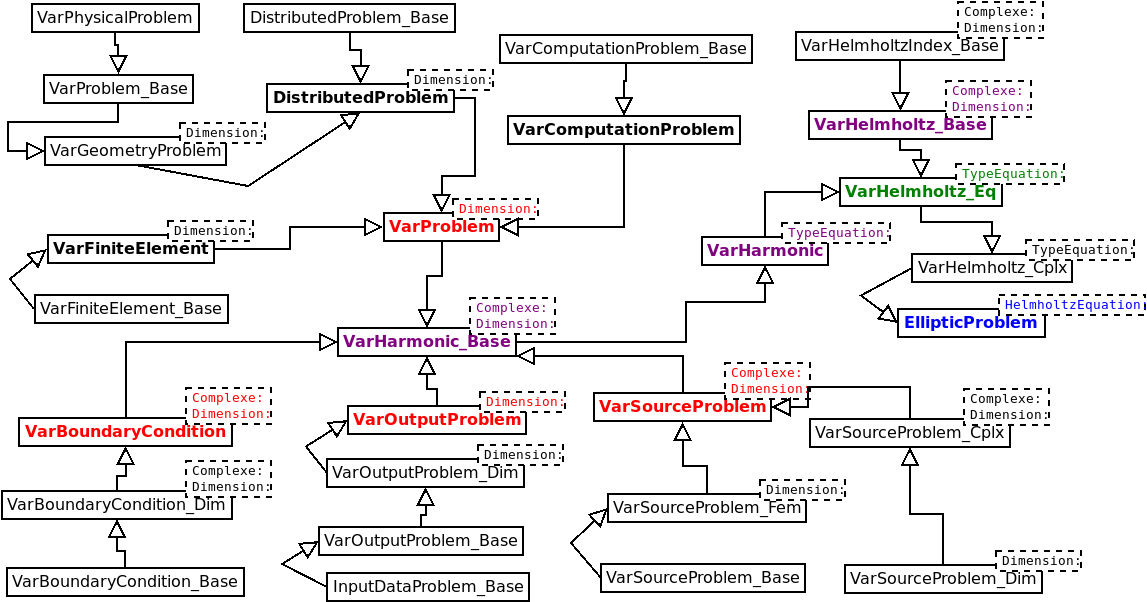
In this diagram, we have shown the final class EllipticProblem for Helmholtz equation, a same kind of inheritance is achieved for other equations (Maxwell's equations, elastodynamics, aeroacoustics). The class HyperbolicProblem contains an object EllipticProblem (attribute var_harmonic), so that you have all what is needed for solving the associated stationary problem. The additional stuff in HyperbolicProblem comprises the treatment of mass matrices (since it has to be inverted for explicit schemes), and different time schemes (explicit, implicit, and local time-stepping).

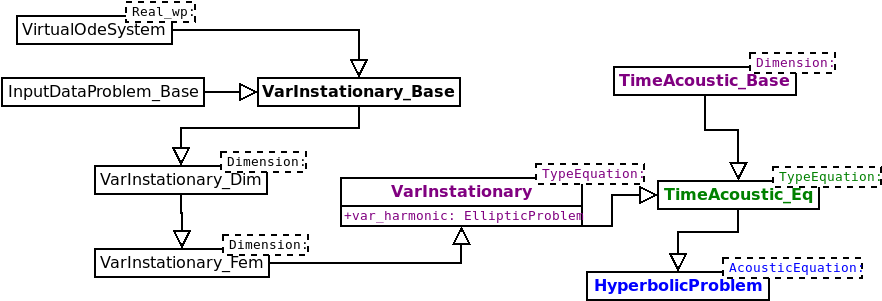
Again the diagram is made explicit for acoustic equation, but the same kind of diagram holds for other unsteady problems (time Maxwell's equations, aeroacoustics in time-domain, etc).