Presentation of the INRIA MC2
team project
The aim of this project is to develop modelling tools for problems involving fluid mechanics in order to explain, to control, to simulate and possibly to predict some complex phenomena coming from physics, chemistry, biology or scientific engineering. The complexity may consist of the model itself, of the coupling phenomena, of the geometry or of non-standard applications. The challenges of the scientific team are to develop stable models and efficient adapted numerical methods in order to recover the main physical features of the considered phenomena. The models will be implemented into numerical codes for practical and industrial applications.
We are interested in both high and low Reynolds number flows, interface and control problems in physics and biology.
Our scientific approach may be described as follows. We first determine some reliable models and then we perform a mathematical analysis (including stability). We then develop the efficient numerical methods, which are implemented for specific applications.
FLUID MECHANICS
Flow control and shape optimization
Fish like swimming.
| This
concerns microfluidics, complex fluids (bifluid
flows, miscible fluids). The challenges are to
obtain reliable models that can be used by our
partner Rhodia (for microfluidics) |
We want
to develop numerical methods in order to address
the complexity of high Reynolds flows. The
challenges are to find scale factors for
turbulent flow cascades, and to develop modern
and reliable methods for computing flows in
aeronautics in a realistic configuration. |
The challenges are the
drag reduction of a ground vehicle, the
reduction of turbomachinery noise emissions or
the increase of lift-to-drag ratio in airplanes,
the control of flow instabilities and the
detection of embedded defects in materials. |
MEDICINE
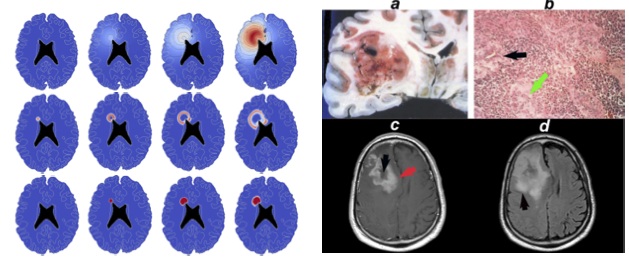
| Based
on clinical images of a given patient (CT scan
or MRI), we develop simple spatial models of
tumor growth (nonlinear partial differential
equations) and numerical methods for resolution
of the inverse problem (parameter estimation)
and try to predict the future fate of a given
tumor (growth, stabilization or regression) in
order to give improve prognosis and therapeutic
decision |
To
gain biological understanding of complex
phenomena, we develop theoretical mathematical
models for various processes of cancer biology
such as avascular and vascular tumor growth but
also development of a cancer disease at the
organism level, integrating the metastatic
process, which represents the major cause of
death in a cancer disease (90%). These models
yield insights about various topics including
anti-angiogenic therapies, metastatic dormancy
or post-surgery metastatic acceleration |
Transdisciplinary
project developing new mathematical models,
numerical tools and experimental protocols to
provide complete understanding of cell
electropermeabilization from the cell to the
tissue scale |
The challenge is to produce patient-specific
simulations starting from medical imaging for growth
of metastasis to the lung of a distant tumor.
Members
Research Scientist
- Sébastien Benzekry [INRIA, Junior Researcher (CR)]
- Michel Bergmann [INRIA, Junior Researcher (CR)]
- Clair Poignard [INRIA, Junior Researcher (CR)]
- Olivier
Saut [CNRS, Junior Researcher (CR)]
Faculty Member
- Afaf Bouharguane
- Charles-Henri Bruneau [ Pr, Université Bordeaux 1, HdR ]
- Thierry Colin [ Team Leader, Pr, Institut Universitaire de France, HdR ]
- Mathieu Colin [ MC, Université Bordeaux 1 ]
- Angelo Iollo [ Pr, Université Bordeaux 1, HdR ]
- Iraj Mortazavi [ MC, Université Bordeaux 1, HdR ]
- Kevin Santugini [ MC, Université Bordeaux 1 ]
- Lisl Weynans [
MC, Université Bordeaux 1 ]
PhD Student
- Florian Bernard
- François Cornélis
- Alexia De Brauer
- Julien Jouganous
- Manuel Latige
- Guillaume Lefèvre
- Michael Leguebe
- Vivien Pianet
- Hervé Ung
- Xin Jin
Post-Doctoral
Fellow
- Julie Joie
- Yong-Liang Xiong
Administrative Assistant
- Anne-Laure Gautier
Associate members
- Patrick Fischer [ MC, Université Bordeaux 1 ]
- Khodor Khadra [ Visiting technical staff ]
- Guy Métivier [ PR, Institut Universitaire de France, HdR ]
- Mazen Saad [ PR, École Centrale Nantes, HdR ]
Invited Member
- Patricio Andrés Cumsille Atala